Verifying the Four Colour Theorem Georges Gonthier Microsoft

Verifying the Four Colour Theorem Georges Gonthier Microsoft Research Cambridge

150 years of history… ¢ ¢ ¢ 1852 Conjecture (Guthrie → De. Morgan) 1878 Publication (Cayley) 1879 First proof (Kempe) 1880 Second proof (Tait) 1890 Rebuttal (Heawood) 1891 Second rebuttal (Petersen) 1913 Reducibility, connexity (Birkhoff) 1922 Up to 25 regions (Franklin) 1969 Discharging (Heesch) 1976 Computer proof (Appel & Haken) 1995 Streamlining (Robertson & al. ) 2004 Self checking proof (Gonthier)

So what about it ? It shows software can be as reliable as math. ¢ It’s been done by applying computer science to mathematics. ¢ The art of computer proving is maturing. ¢

Outline ¢ The Four Colour Theorem what it says l how it’s proved l ¢ Formal proofs proving with programs l thinking with programs l ¢ Computer proofs l how it’s done

The Theorem open and connected disjoint subsets of R x R Every simple planar map can be colored with only four colors ∃good covering map with at most four regions adjacent regions covered with different colors have a common border point that is not a corner touches more than two regions

The formal theorem Definition covers (m, m' : map) : = ∀z : point, subregion (m z) (m' z). Definition size_at_most n m : = ∃ f, ∀ z, inmap m z → ∃2 i, i < n & m (f i). Definition border m z 1 z 2 : = intersect (closure (m z 1)) (closure (m z 2)). Definition corner_map (m : map) z : map : = fun z 1 z 2 ⇒ m z 1 z 2 ∧ closure (m z 1) z. Definition not_corner m z : = size_at_most 2 (corner_map m z). Definition adjacent m z 1 z 2 : = meet (not_corner m) (border m z 1 z 2). Record simple_map (m : map) : Prop : = Simple. Map { simple_map_proper : > proper_map m; map_open : ∀z, open (m z); map_connected : ∀z, connected (m z) }. Record coloring (m, k : map) : Prop : = Coloring { coloring_proper : > proper_map k; coloring_inmap : subregion (inmap k) (inmap m); coloring_covers : covers m k; coloring_adj : ∀z 1 z 2, k z 1 z 2 → adjacent m z 1 z 2 → m z 1 z 2 }. Definition map_colorable n m : = ∃2 k, coloring m k & size_at_most n k. Theorem four_color : ∀m, simple_map m → map_colorable 4 m.

Outline ¢ The Four Colour Theorem what it says l how it’s proved l ¢ Formal proofs proving with programs l thinking with programs l ¢ Computer proofs l how it’s done

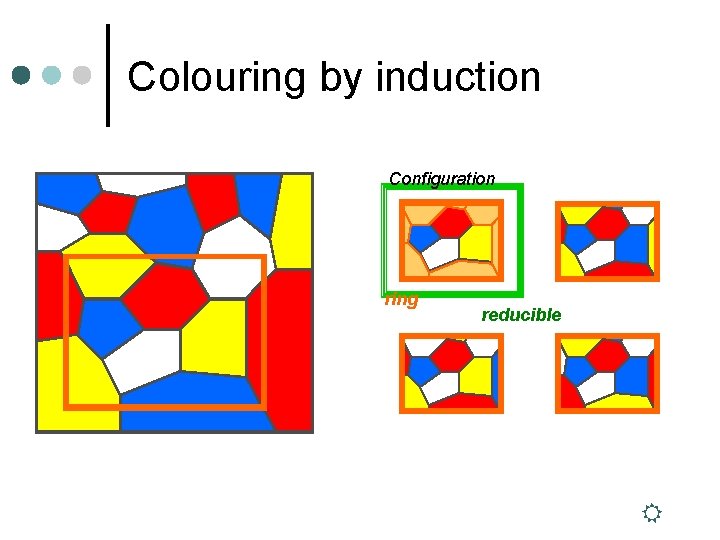
Colouring by induction Configuration ring reducible

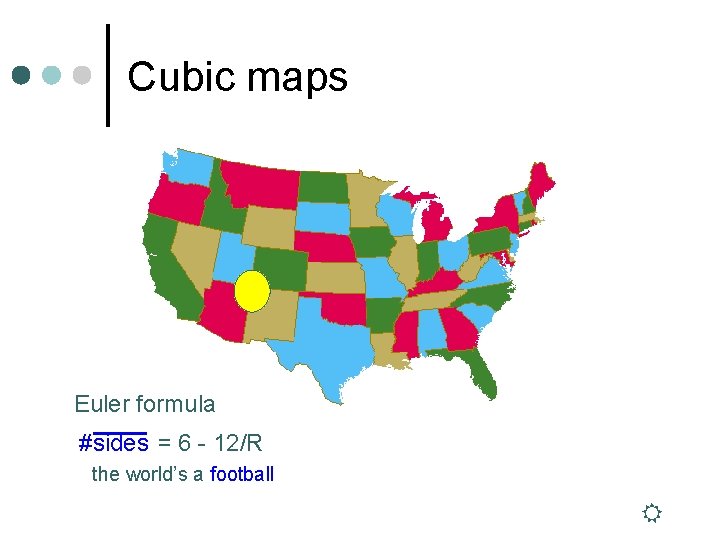
Cubic maps Euler formula #sides 2 E/R 12/R R + N=– 6 E- = 2 the world’s a football

Small rings Any non-trivial ring < 6 defines reducible configurations (Birkhoff, 1913) ¢ If there are no small rings, then all 2 neighborhoods are double rings ¢ look for configurations in 2 -neighborhoods!

The proof in a nutshell Find a set of configurations such that: s e s (A) reducibility: Each one can be a c 0 0 0 , any planar ring coloured to match 0 0 0 , 0 0 colouring. 0 , 1 s e s (B) unavoidability: At least one a c 0 0 0 appears 10, in any planar map. ¢ Verify that the combinatorics fit the topology (graph theory + analysis). ¢

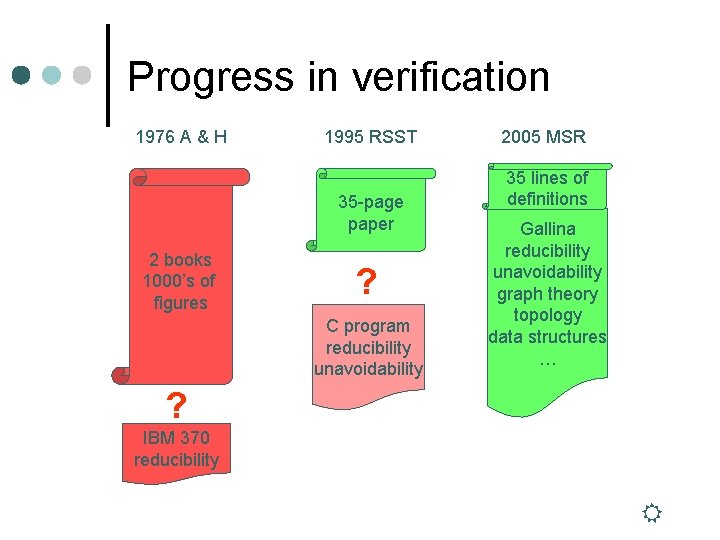
Progress in verification 1976 A & H 1995 RSST 35 -page paper 2 books 1000’s of figures ? C program reducibility unavoidability 2005 MSR 35 lines of definitions Gallina reducibility unavoidability graph theory topology data structures … ? IBM 370 reducibility

Outline ¢ The Four Colour Theorem what it says l how it’s proved l ¢ Formal proofs proving with programs l thinking with programs l ¢ Computer proofs l how it’s done

The Poincaré principle ¢ ¢ How do you prove: 2+2=4 ? Given 2 ≝ 1+ (1+ 0) 4 ≝ 1+ (1+ (1+ 0))) n + m ≝ if n is 1+ n’ then 1+ (n’ + m) else m (a recursive program) a: 0+2=2 b: (1 + 0) + 2 = 1 + (0 + 2) (neutral left) (associativity) c: 2 + 2 = 1 + ((1 + 0) + 2) (def, associativity) d: 2 + 2 = 1 + (0 + 2)) (replace b in c) a: e: (def, calculation) (replace a in d, def)

Reflecting reducibility ¢ Setup Variable cf : config. Definition cfreducible : Prop : = … Definition check_reducible : bool : = … Lemma check_reducible_valid : check_reducible -> cfreducible. ¢ Usage s e as c 0 0 H 1 Y 3 H 11 Y 4 H 0 9, H 0 1 Y 3 H 9 Y 6 Y 1 Y 3 Y 1 Y). 0 0 , Proof. apply check_reducible_valid; by compute. Qed. 20 Lemma cfred 232 : cfreducible (Config 11 33 37 H 2 H 13 Y 5 H 10

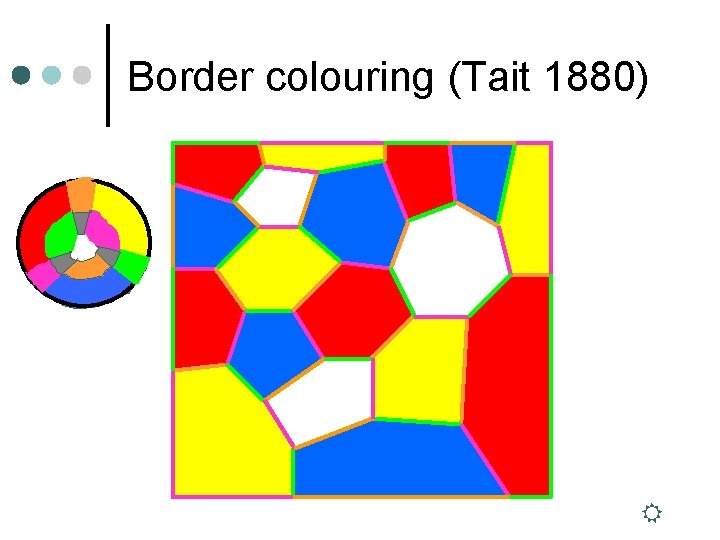
Border colouring (Tait 1880)

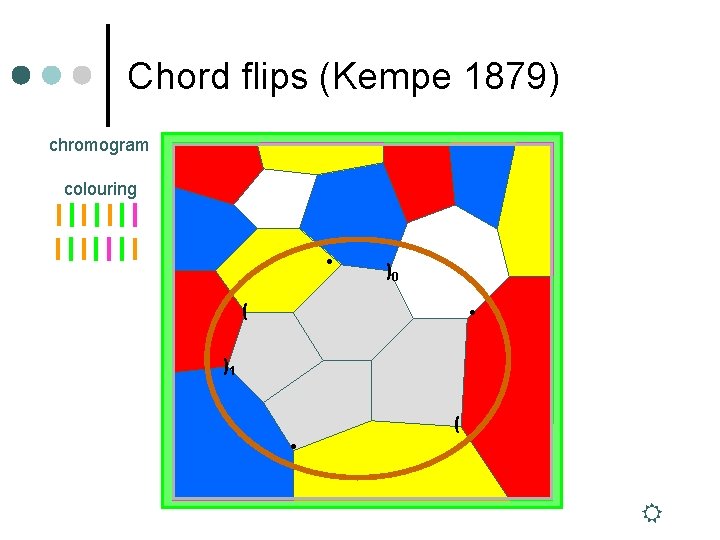
Chord flips (Kempe 1879) chromogram colouring • )0 ( • )1 ( •

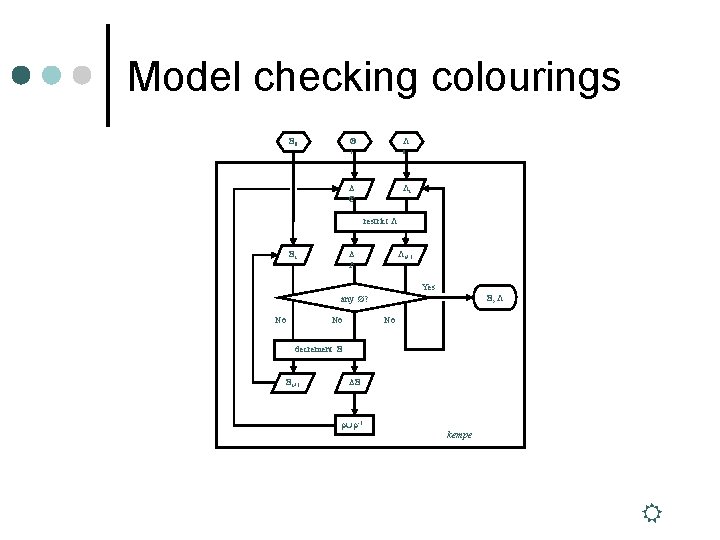
Model checking colourings Ξ 0 Λ 1 0 Λi restrict Λ Λ Ξi Λi+1 Yes Ξ, Λ any ? No No No decrement Ξ Ξi+1 Ξ -1 kempe

Chromogram twiddling Fixpoint gram_neg_rec (n : nat) (w : chromogram) {struct w} : chromogram : = match w, n with | Adds Gpush w', _ => Adds Gpush (gram_neg_rec (S n) w') | Adds Gskip w', _ => Adds Gskip (gram_neg_rec n w') | Adds s w', S n => Adds s (gram_neg_rec n w') | Adds Gpop 0 w', O => Adds Gpop 1 w' | Adds Gpop 1 w', O => Adds Gpop 0 w' | seq 0, _ => w end. Definition gram_neg : = gram_neg_rec 0.

Correctness proof Lemma match_gram_neg : forall b 0 et w, matchg (Seq b 0) et (gram_neg w) = matchg (Seq (¬ b 0)) et w. Proof. move => b 0 et w; set sb : bitseq : = seq 0. have Esb: forall b : bool, Adds b sb = add_last sb b by done. rewrite /gram_neg -[0]/(size sb) 2!{}Esb. elim: w et sb => [|s w IHw] et lb; first by case lb. case Ds: s; (case: et => [|e et]; first by case lb); first [ by case: e (IHw et (Adds _ lb)) => /= | by case: e; case: lb => [|b lb]; rewrite /= ? if_negb ? IHw ]. Qed.

Outline ¢ The Four Colour Theorem what it says l how it’s proved l ¢ Formal proofs proving with programs l thinking with programs l ¢ Computer proofs l how it’s done

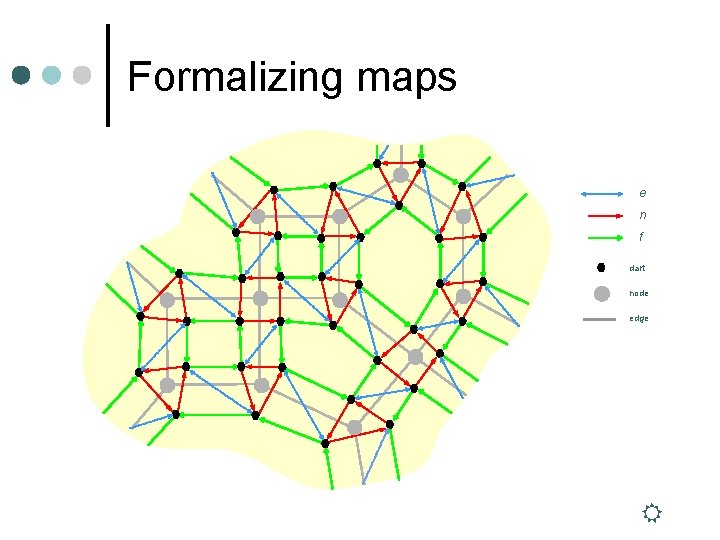
Formalizing maps e n f dart node edge

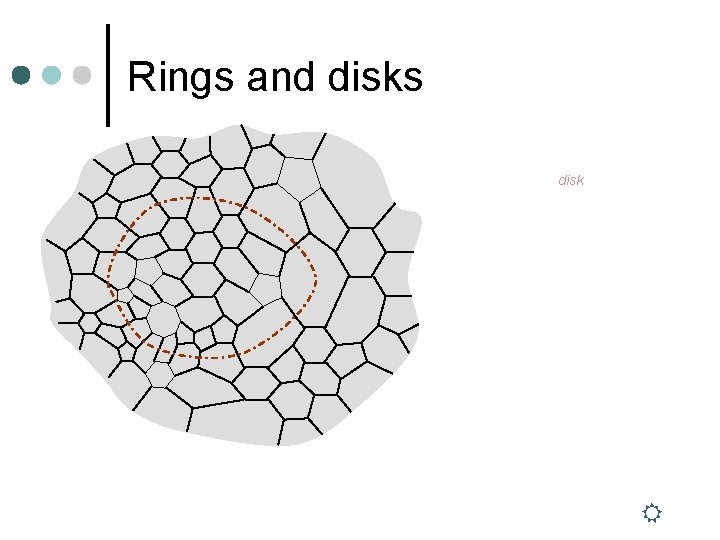
Rings and disks disk rest

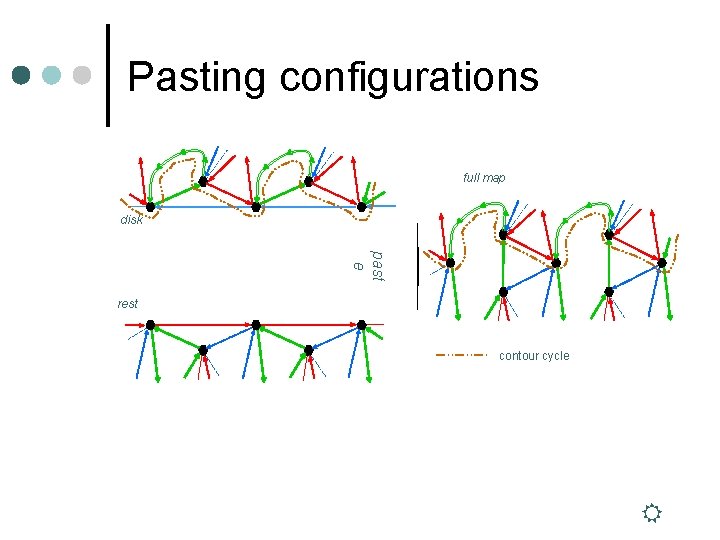
Pasting configurations full map disk past e rest contour cycle

Folkloric proofs? (3. 3) Let K be a configuration appearing in a triangulation T, and let S be the free completion of K. Then there is a projection ɸ of S into T such that ɸ (x) = x for all x ∈ V(G(K)) ∪ E(G(K)) ∪ F(G(K)). This is a “folklore” theorem, and we omit its [lengthy] proof… Definition phi x : = if ac x then h x else if ac (edge x) then edge (h (edge x)) else if ac (node x) then face (edge (h (node x))) else edge (node (h (node (edge x))))).

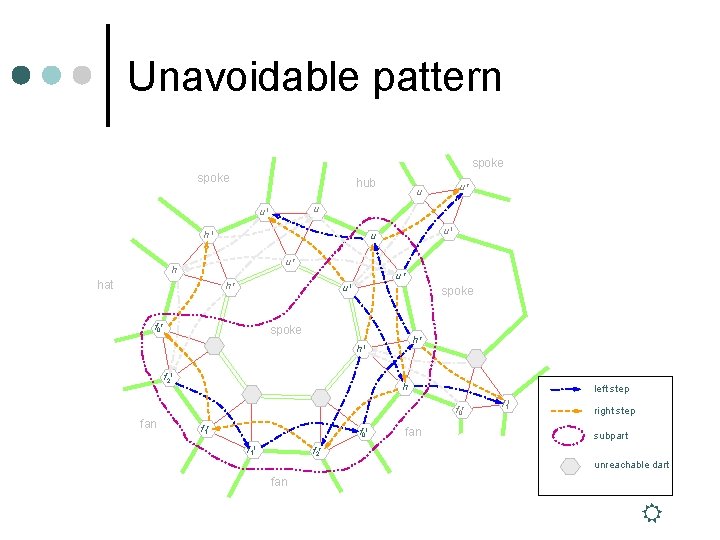
Unavoidable pattern spoke hub ur u u ul hl ul u ur h hat ur hr ul f 0 r spoke hr hl f 2 l h left step f 0 r fan f 1 r f 0 l f 1 l fan f 1 l right step subpart f 2 r unreachable dart fan

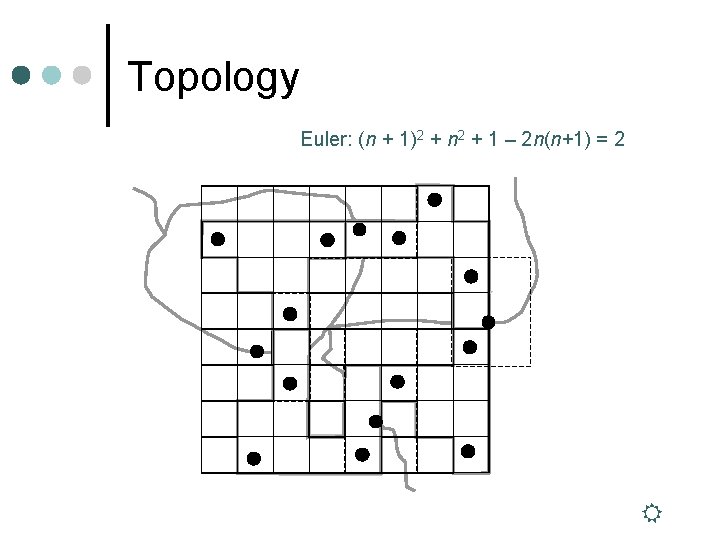
Topology Euler: (n + 1)2 + n 2 + 1 – 2 n(n+1) = 2

Outline ¢ The Four Colour Theorem what it says l how it’s proved l ¢ Formal proofs proving with programs l thinking with programs l ¢ Computer proofs l how it’s done

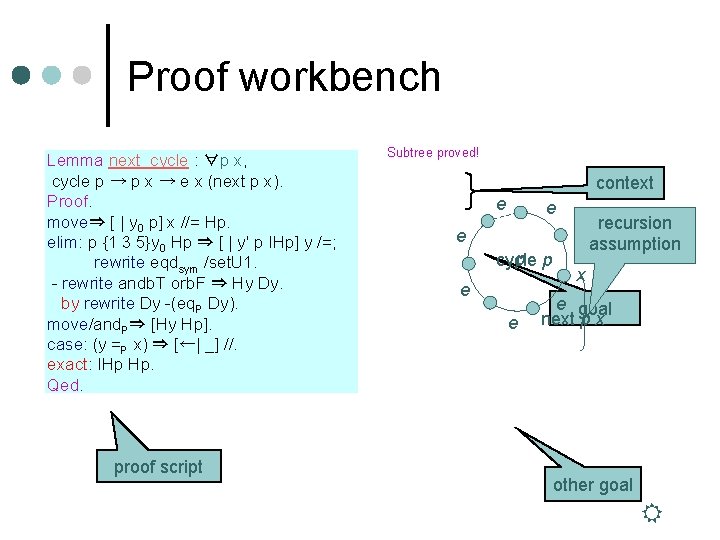
Proof workbench Lemma next_cycle : ∀p x, cycle p → p x → e x (next p x). Proof. move⇒ [ | y 0 p] x //= Hp. elim: p {1 3 5}y 0 Hp ⇒ [ | y' p IHp] y /=; rewrite eqdsym /set. U 1. - rewrite andb. T orb. F ⇒ Hy Dy. by rewrite Dy -(eq. P Dy). move/and. P⇒ [Hy Hp]. case: (y =P x) ⇒ [←| _] //. exact: IHp Hp. Qed. proof script 2 subgoals 1 Subtree subgoal proved! d : data. Set context e : rel d e e ============== y 0 : d recursion xp forall : dseq (pd: seq d) (x : d), cycle p -> p x -> e assumption yxe : x: dd(next p x) y’ e p p y 0) cycle p ============== p Hp: seq Hy : epath ydy 0 y 0 (add_last x ============== Dy IHp e y: : y 0 yforall =d &&x true x 0 : d, ============== set. U 1 -> (ypath =d y 0 p x)x 0 xe ||-> (add_last false e x (next_at p y 0) x y 0 p) ->xe(if e -> x y(if set. U 1 =d y =d x then x 0 x then p y 0 x y 0 else x)ex) goal next -> e x (next_ate x y 0 x 0 p) p x subgoal y : d 2 is: e. Hy ============== y y’ : e&& y y’path y’ (add_last p y 0) -> Hp e or 3 b y: y’path && (y =d y’ path (add_last x) y’ (y’(add_last (y' =d x) p y 0) (p x) p y 0) -> ============== ->eeor 3 b xx(if (ify(y y=d =d =dxxx)then (y’ =d y’y’ x) (p x) -> e xfalse or 3 b (yelse (if=d y (y’ =d x) next_at (y’ =d x then =d x) x(p x)y’ y 0 x) (py’x)p) -> e x (next_at (if else y =d next_at x xthen y 0 xy’y’y 0 p) y’ p) else next_at x y 0 y’ p) other goal

Five tactic summary move: x y Hxy … => z t Hzt … bookkeeping : context goal moves case: x Hxy … => [a | b c] … decomposition, induction (with elim) rewrite /= orb. F –[x]addn 0 … partial evaluation, simplification apply: lemma… => [x y Hxy | n | …] … match goal (backward chaining) have label: conjecture by … set goal (forward chaining)

Some conclusions Proof assistants can give real proofs of real theorems ¢ Machine formalization can lead to new mathematical insights ¢ Formally proving programs can be easier than formally proving theorems ¢