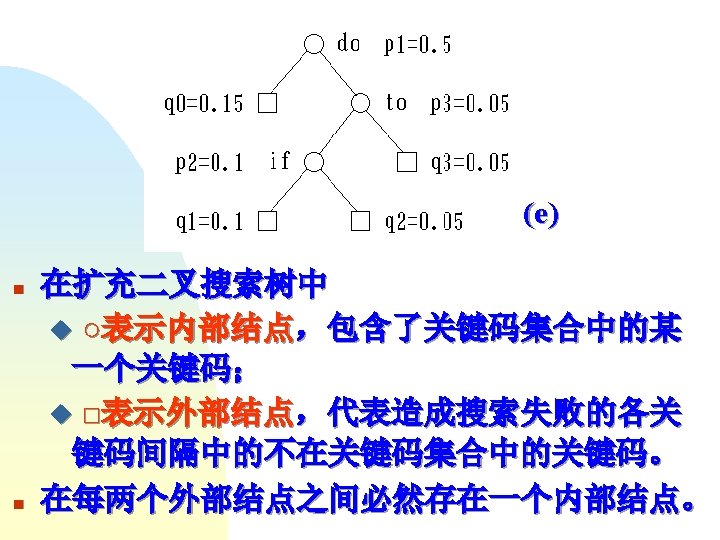
Venn Set Template class Type class Set Set









![for ( int i = 0; i < Max. Size; i++ ) bit. Vector[i] for ( int i = 0; i < Max. Size; i++ ) bit. Vector[i]](https://slidetodoc.com/presentation_image_h/fccdeb7a854d0a21b7ee6880e1dfb0f0/image-10.jpg)


















































































![第二步 C W R 左子树 右子树 115 90 1 T[0, 0] T[1, 2] 165 第二步 C W R 左子树 右子树 115 90 1 T[0, 0] T[1, 2] 165](https://slidetodoc.com/presentation_image_h/fccdeb7a854d0a21b7ee6880e1dfb0f0/image-108.jpg)
![第三步 C W R 左子树 右子树 150 100 1 T[0, 0] T[1, 3] 190 第三步 C W R 左子树 右子树 150 100 1 T[0, 0] T[1, 3] 190](https://slidetodoc.com/presentation_image_h/fccdeb7a854d0a21b7ee6880e1dfb0f0/image-109.jpg)



























![0 parent -5 1 2 0 3 1 4 2 3 Parent[0] Parent[4] Parent[1] 0 parent -5 1 2 0 3 1 4 2 3 Parent[0] Parent[4] Parent[1]](https://slidetodoc.com/presentation_image_h/fccdeb7a854d0a21b7ee6880e1dfb0f0/image-151.jpg)



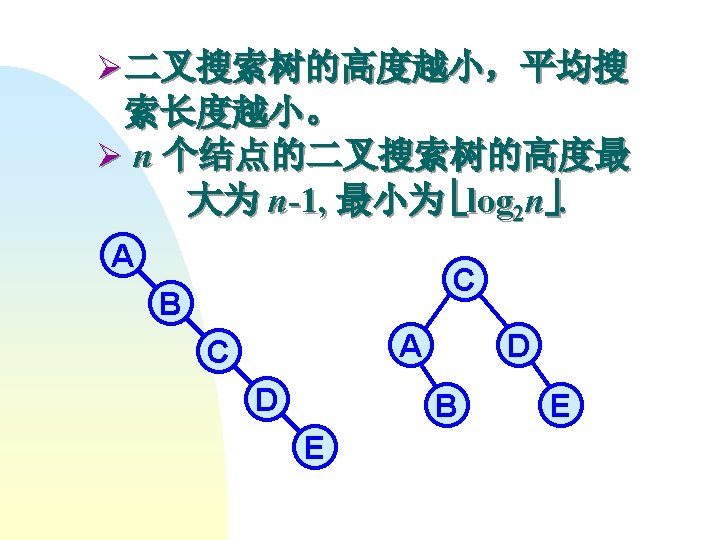

- Slides: 163




集合运算的文氏(Venn)图 集合(Set)的抽象数据类型 Template <class Type> class Set { Set ( int Max. Set. Size ) : Max. Size ( Max. Set. Size ); void Make. Empty ( Set &s ); int Add. Member ( Set &s, const Type x ); int Del. Member ( Set &s, const Type & x );

void Assign ( Set& s 1, Set& s 2 ); void Union ( Set& s 1, Set& s 2 ); void Intersection ( Set& s 1, Set& s 2 ); void Difference ( Set& s 1, Set& s 2 ); int Contains ( Set &s, const Type & x ); int Equal ( Set &s 1, Set &s 2 ); int Sub. Set ( Set &s 1, Set &s 2 ); }


private: int * bit. Vector; int Max. Size; public: Set ( int Max. Set. Size = Default. Size ); ~Set ( ) { delete [ ] bit. Vector; } void Make. Empty ( ) { for ( int i = 0; i < Max. Size; i++ ) bit. Vector[i] = 0; } int Add. Member ( const int x ); int Del. Member ( const int x ); Set& operator = ( Set & right );

Set& operator + ( Set & right ); Set& operator * ( Set & right ); Set& operator - ( Set & right ); int Contains ( const int x ); int Sub. Set ( Set & right ); int operator == ( Set & right ); }; 使用示例 Set s 1, s 2, s 3, s 4, s 5; int index, equal; //构造集合 for ( int k = 0; k < 10; k++ ) //集合赋值 { s 1. Add. Member( k ); s 2. Add. Member( k +7 ); } // s 1 : { 0, 1, 2, …, 9 }, s 2 : { 7, 8, 9, …, 16 }

s 3 = s 1 + s 2; //求s 1与s 2的并 { 0, 1, …, 16 } s 4 = s 1 * s 2; //求s 1与s 2的交 { 7, 8, 9 } s 5 = s 1 - s 2; //求s 1与s 2的差 { 0, 1, 2, 3, 4, 5, 6 } index = s 1. Sub. Set ( s 4 ); //求s 4在s 1中首次匹配 cout << index << endl; //位置, index = 7 equal = s 1 == s 2; //集合s 1与s 2比较相等 cout << equal << endl; //equal为 0, 两集合不等 用位向量实现集合时部分操作的实现 Set : : Set (int Max. Set. Size) : Max. Size (Max. Set. Size) { assert ( Max. Size > 0 ); bit. Vector = new int [Max. Size]; assert ( bit. Vector != 0 );
![for int i 0 i Max Size i bit Vectori for ( int i = 0; i < Max. Size; i++ ) bit. Vector[i]](https://slidetodoc.com/presentation_image_h/fccdeb7a854d0a21b7ee6880e1dfb0f0/image-10.jpg)
for ( int i = 0; i < Max. Size; i++ ) bit. Vector[i] = 0; } int Set : : Addmember ( const int x ) { assert ( x >= 0 && x < Max. Size ); if ( ! bit. Vector[x] ) { bit. Vector[x] = 1; return 1; } return 0; } int Set : : Del. Member ( const int x ) { assert ( x >= 0 && x < Max. Size ); if ( bit. Vector[x] ) { bit. Vector[x] = 0; return 1; } return 0; }

Set& Set : : operator = ( Set& right ) { assert ( Max. Size == right. Max. Size ); for ( int i =0; i <Max. Size; i++ ) bit. Vector[i] = right. bit. Vector[i]; return *this; } Set& Set : : operator + ( Set& right ) { assert ( Max. Size == right. Max. Size ); for ( int i = 0; i < Max. Size; i++ ) bit. Vector[i] = bit. Vector[i] || right. bit. Vector[i]; return *this; }

Set& Set : : operator * ( Set & right ) { assert ( Max. Size == right. Max. Size ); for ( int i = 0; i < Max. Size; i++) bit. Vector[i] = bit. Vector[i] && right. bit. Vector[i]; return *this; } Set& Set : : operator - ( Set & right ) { assert ( Max. Size == right. Max. Size ); for ( int i = 0; i < Max. Size; i++ ) bit. Vector[i] = bit. Vector[i] && !right. bit. Vector[i]; return *this; }

int Set : : Contains ( const int x ) { assert ( x >= 0 && x < Max. Size ); return bit. Vector[x]; } int Set : : operator == ( Set & right ) { assert ( Max. Size == right. Max. Size ); for ( int i = 0; i < Max. Size; i++) if ( bit. Vector[i] != right. bit. Vector[i] ) return 0; return 1; } int Set : : Sub. Set (Set & right ) { assert ( Max. Size == right. Max. Size );



template <class Type> class Set. Node { friend class Set. List<Type>; public: Set. Node (const Type & item ) : data (item), link (NULL); private: Type data; Set. Node<Type> *link; }; template <class Type> class Set. List { private: Set. Node<Type> *first, *last; public:

Set. List ( ); void Make. Empty ( ); int Add. Member ( const Type & x ); int Del. Member ( const Type & x ); Set. List<Type> & operator = ( Set. List<Type> & right ); Set. List<Type> & operator + ( Set. List<Type> & right ); Set. List<Type> & operator * ( Set. List<Type> & right ); Set. List<Type> & operator - ( Set. List<Type> & right ); int Contains ( const Type & x );

int operator == ( Set. List<Type> & right ); Type & Min ( ); Type & Max ( ); } 集合构造函数 template <class Type> void Set. List<Type> : : Set. List ( ) { Set. Node<Type> *first = *last = new Set. Node<Type>(0); }

集合的搜索、加入和删除操作 template <class Type> int Set. List<Type> : : Contains (const Type & x ) { Set. Node<Type> *temp = first→link; while ( temp != NULL && temp→data < x ) temp = temp→link; if (temp != NULL && temp→data == x) return 1; else return 0; }

template <class Type> int Set. List<Type> : : Add. Member ( const Type & x ) { Set. Node<Type> *p = first→link, *q = first; while ( p != NULL && p→data < x ) { q = p; p = p→link; } if ( p != NULL && p→data == x ) return 0; Set. Node<Type> *s = new Set. Node (x); s→link = p; q→link = s; if ( p == NULL ) last = s; return 1; }

template <class Type> int Set. List<Type> : : Del. Member ( const Type & x ) { Set. Node<Type> *p = first→link, *q = first; while ( p != NULL && p→data < x ) { q = p; p = p→link; } if ( p != NULL && p→data == x ) { q→link = p→link; if ( p == last ) last = q; delete p; return 1; } else return 0; }

用有序链表表示集合时的几个重载函数 template <class Type> Set. List<Type>& Set. List <Type> : : operator = ( Set. List<Type> & right ) { Set. Node<Type>*pb = right. first→link; Set. Node<Type>*pa = first = new Set. Node<Type>; while ( pb != NULL ) { pa→link = new Set. Node<Type> (pb→data); pa = pa→link; pb = pb→link; } pa→link = NULL; last = pa; return *this; }

template <class Type> Set. List<Type>& Set. List<Type> : : operator + ( Set. List<Type> & right ) { Set. Node<Type> *pb = right. first→link; Set. Node<Type> *pa = first→link; Set. Node<Type> *pc = first; while ( pa != NULL && pb != NULL ) { if ( pa→data == pb→data ) { pc→link = pa; pa = pa→link; pb = pb→link; } else if ( pa→data < pb→data ) { pc→link = pa; pa = pa→link; } else

{ pc→link = new Set. Node<Type> (pb→data); pb = pb→link; } pc = pc→link; } if ( pa != NULL ) pc→link = pa; else { while ( pb != NULL ) { pc→link = new Set. Node<Type> (pb→data); pc = pc→link; pb = pb→link; } pc→link = NULL; last = pc; } return *this; }

template <class Type> Set. List<Type>& Set. List<Type>: : operator * ( Set. List<Type> & right ) { Set. Node<Type> *pb = right. first→link; Set. Node<Type> *pa = first→link; Set. Node<Type> *pc = first; while ( pa != NULL && pb != NULL ) { if ( pa→data == pb→data ) { pc = pc→link; pa = pa→link; pb = pb→link; } else if ( pa→data < pb→data ) { pc→link = pa→link; delete pa; pa = pc→link; } else pb = pb→link; }

while ( pa != NULL ) { pc→link = pa→link; delete pa; pa = pc→link; } last = pc; return *this; } template <class Type> Set. List<Type>& Set. List<Type> : : operator - ( Set. List<Type> & right ) { Set. Node<Type> *pb = right. first→link; Set. Node<Type> *pa = first→link;

Set. Node<Type> *pc = first; while ( pa != NULL && pb != NULL ) { if ( pa→data == pb→data ) { pc→link = pa→link; delete pa; pa = pc→link; pb = pb→link; } else if ( pa→data < pb→data ) { pc = pc→link; pa = pa→link; } else pb = pb→link; } if ( pa == NULL ) last = pc; return *this; }

template <class Type> int Set. List<Type> : : operator == ( Set. List<Type> & right ) { Set. Node<Type> *pb = right. first→link; Set. Node<Type> *pa = first→link; while ( pa != NULL && pb != NULL ) if ( pa→data == pb→data ) { pa = pa→link; pb = pb→link; } else return 0; if ( pa != NULL || pb != NULL ) return 0; return 1; }









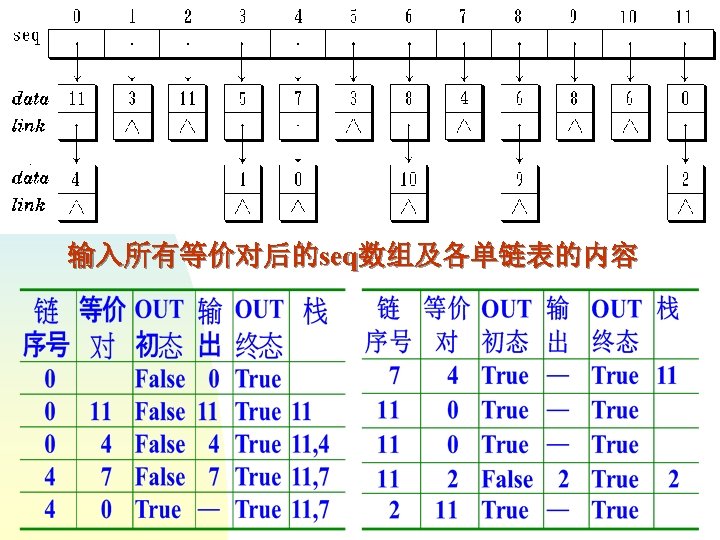
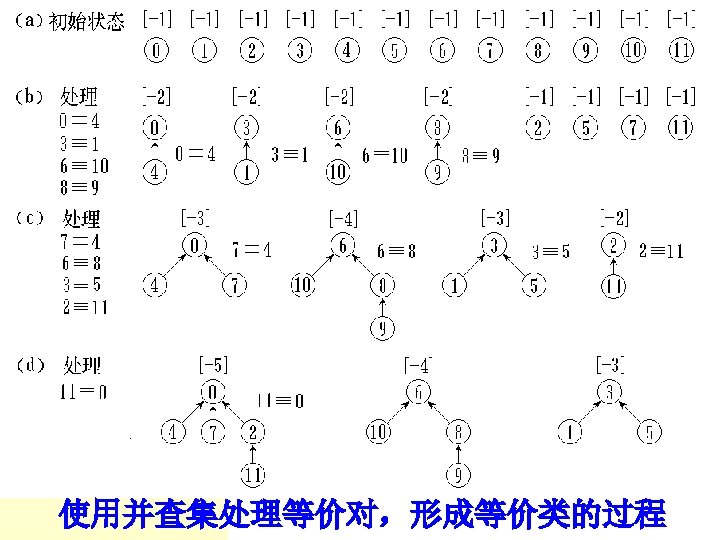
等价类链表的定义 enum Boolean { False, True }; class List. Node { //定义链表结点类 friend void equivalence ( ); private: int data; //结点数据 List. Node *link; //结点链指针 List. Node ( int d ) { data = d; link = NULL; } }; typedef List. Node *List. Node. Ptr;






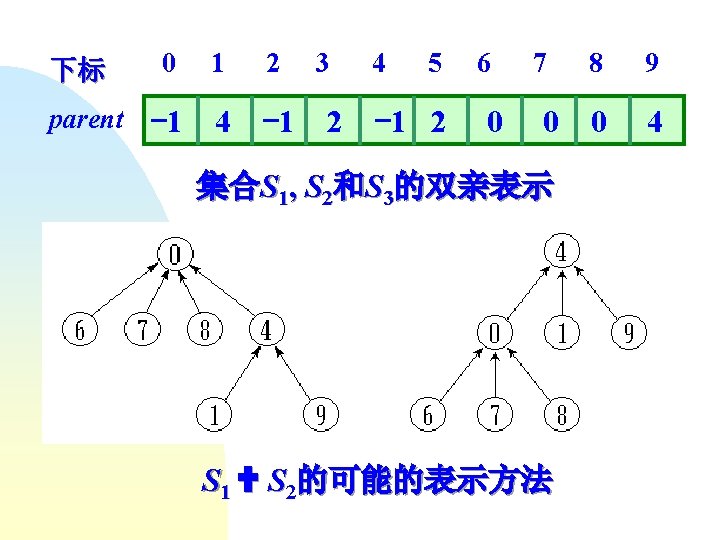
const int Default. Size = 10; class UFSets { //并查集的类定义 public: UFSets ( int s = Default. Size ); ~UFSets ( ) { delete [ ] parent; } const UFSets & operator = ( UFSets const & Value ); void Union ( int Root 1, int Root 2 ); int Find ( int x ); void Union. By. Height ( int Root 1, int Root 2 ); private: int *parent; int size; };

UFSets : : UFSets ( int s ) { //构造函数 size = s; parent = new int [size+1]; for ( int i = 0; i <= size; i++ ) parent[i] = -1; } unsigned int UFSets : : Find ( int x ) { //搜索操作 if ( parent[x] <= 0 ) return x; else return Find ( parent[x] ); } void UFSets : : Union ( int Root 1, int Root 2 ) { //并 parent[Root 2] = Root 1; //Root 2指向Root 1 }



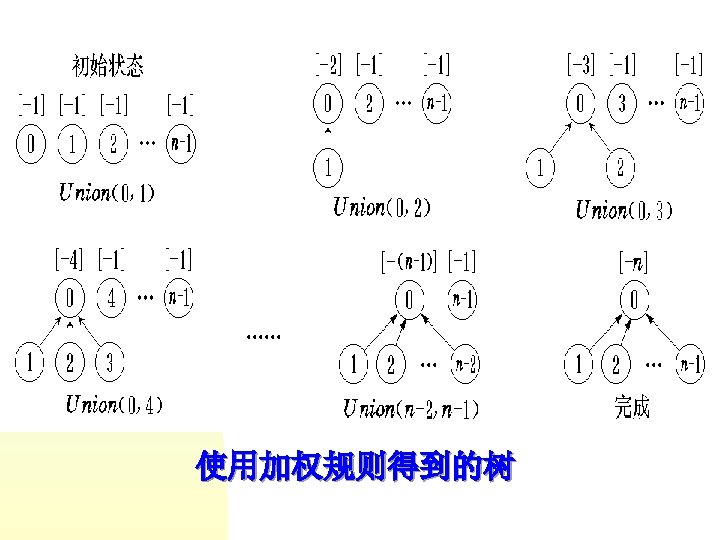
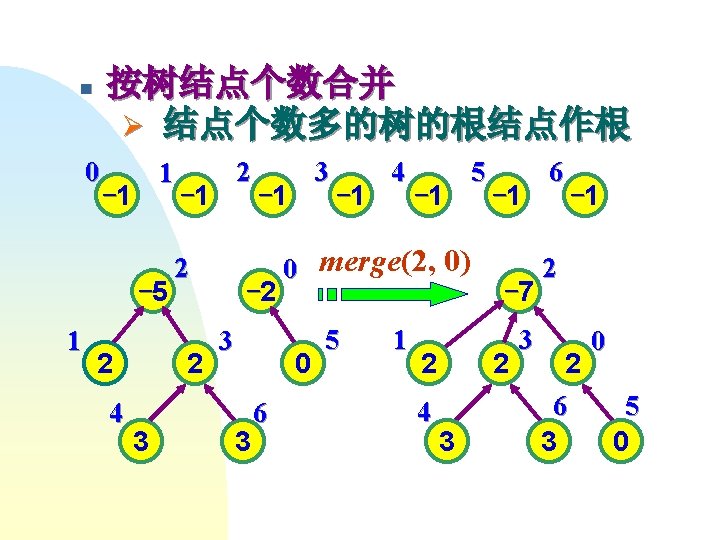
void UFSets : : Weighted. Union ( int Root 1, int Root 2 ) { //按Union的加权规则改进的算法 int temp = parent[Root 1] + parent[Root 2]; if ( parent[Root 2] < parent[Root 1] ) { parent[Root 1] = Root 2; //Root 2中结点数多 parent[Root 2] = temp; //Root 1指向Root 2 } else { parent[Root 2] = Root 1; //Root 1中结点数多 parent[Root 1] = temp; //Root 2指向Root 1 } }







静态搜索表 template <class Type> class data. List; template <class Type> class Node { friend class data. List<Type>; public: Node ( const Type & value ) : key ( value ) { } Type get. Key ( ) const { return key; } void set. Key ( Type k ) { key = k; } private: Type key; other; };

template <class Type> class data. List { public: data. List ( int sz = 10 ) : Array. Size (sz), Element (new Node <Type > [sz]) { } virtual ~data. List ( ) { delete [ ] Element; } friend ostream &operator << (ostream & Out. Stream, const data. List<Type> & Out. List ); friend istream & operator >> ( istream & In. Stream, data. List<Type> & In. List ); protected: Type *Element; int Array. Size, Current. Size; };

template <class Type> class search. List : public data. List<Type> { //作为派生类的静态搜索表的类定义 public: search. List ( int sz = 10 ) : data. List<Type> (sz) { } virtual ~search. List ( ) { } virtual int Search ( const Type & x ) const; };

template <class Type> istream & operator >> ( istream & In. Stream, data. List<Type> & In. List ) { //从输入流对象In. Stream输入数据到数据表In. List cout << “输入数组当前大小 : ”; Instream >> In. List. Current. Size; cout << “输入数组元素值 : n”; for ( int i = 0; i < In. List. Current. Size; i++ ) { cout << “元素 ” << i << “ : ”; In. Stream >> In. List. Element[i]; } return In. Stream; }

template <class Type> ostream & operator << ( ostream & Out. Stream, const data. List<Type> & Out. List ) { //将数据表Out. List内容输出到输出流对象Out. Stream << “数组内容 : n”; for ( int i = 0; i < Out. List. Current. Size; i++ ) Out. Stream << Out. List. Element[i] << ‘ ’; Out. Stream << endl; Out. Stream << “数组当前大小 : ” << Out. List. Current. Size << endl; return Out. Stream; }



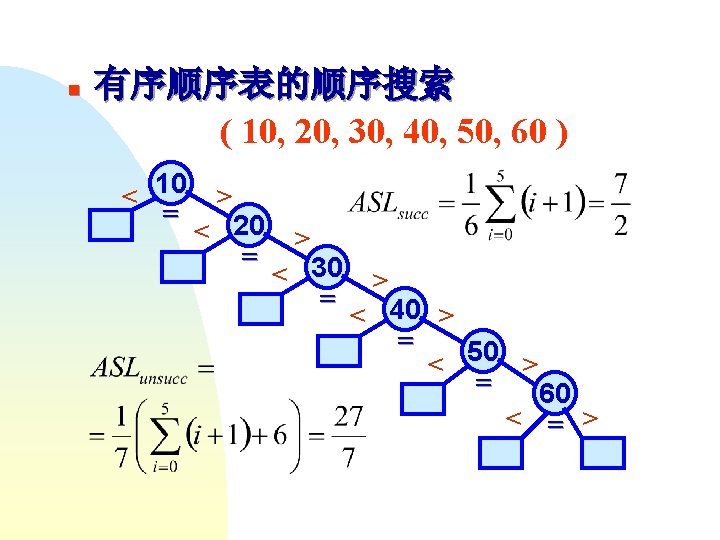
template <class Type> int search. List<Type> : : Search ( const Type & x ) const { //顺序搜索的迭代算法,0号元素为监视哨 Element[0]. set. Key ( x ); int i = Current. Size; while (Element[i]. get. Key ( ) != x ) i --; return i; } template <class Type> int earch. List<Type> : : Search ( const Type & x, int & loc ) const { //顺序搜索的递归算法 if ( loc >= Current. Size ) return -1; else if ( Element[loc]. get. Key( ) == x ) return loc; else return Search ( x, loc+1 ); }

const int Size = 10; main ( ) { //顺序搜索的主过程 search. List<float> List 1 (Size); float Target; int Location; cin >> List 1; cout << List 1; //输入/输出数据表List 1 cout << “搜索浮点数 : ”; cin >> Target; if ( ( Location = List 1. search (Target ) ) != 0 ) cout << “ 找到下标 ” << Location << endl; else cout << “ 没有找到. n”; }




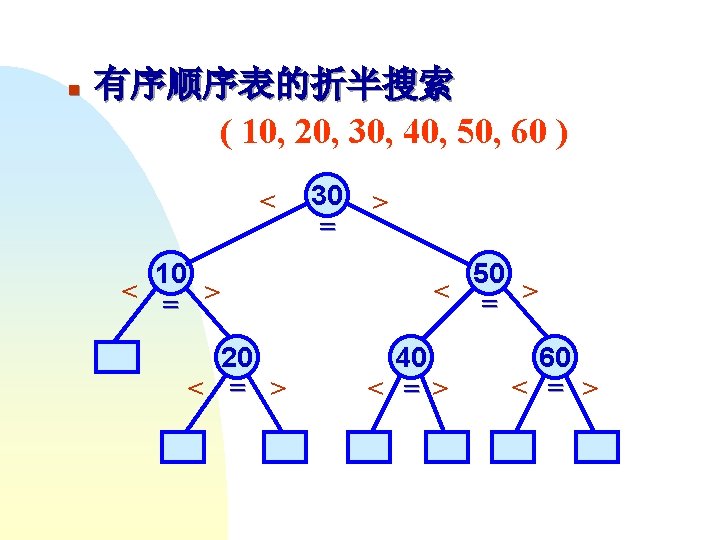
template <class Type> class ordered. List : public data. List<Type> { //有序表的类定义, 继承了数据表 public: ordered. List (int sz = 10) : data. List<Type> (sz) { } virtual ~ordered. List ( ) { } virtual int Search ( const Type & x ) const; };

template <class Type> int ordered. List<Type> : : Binary. Search ( const Type & x, const int low, const int high ) const { //折半搜索的递归算法 int mid = -1; if ( low <= high ) { mid = ( low + high ) / 2; if ( Element[mid]. get. Key( ) < x ) mid = Binary. Search ( x, mid +1, high ); else if ( Element[mid]. get. Key( ) > x ) mid = Binary. Search ( x, low, mid -1 ); } return mid; }

template <class Type> in ordered. List <Type>: : Binary. Search ( const Type & x ) const { //折半搜索的迭代算法 int high = Current. Size-1, low = 0, mid; while ( low <= high ) { mid = ( low + high ) / 2; if ( Element[mid]. get. Key ( ) < x ) low = mid + 1; else if ( Element[mid]. get. Key ( ) > x ) high = mid - 1; else return mid; } return -1; }





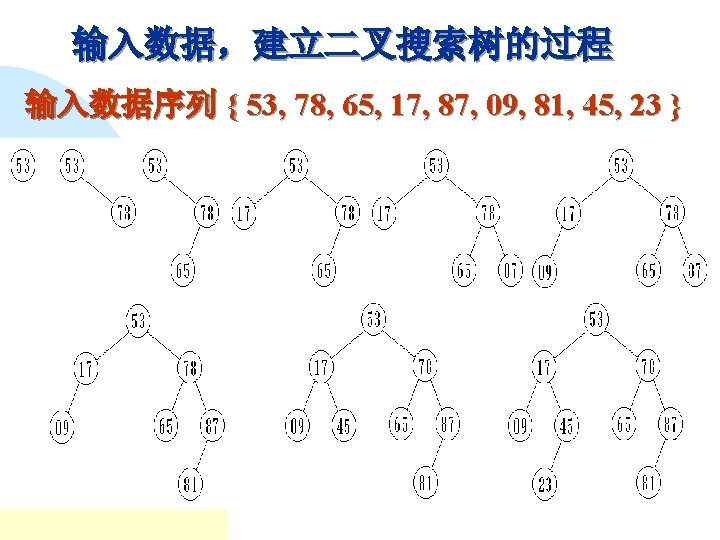
template <class Type> Class Bst. Node <Type>: public Bin. Tree. Node { //二叉搜索树结点类 friend class BST <Type>; public: Bst. Node ( ) : left. Child (NULL), right. Child (NULL) { } Bst. Node ( const Type d ) : data (d), left. Child (NULL), right. Child (NULL) { } Bst. Node ( const Type d = 0, Bst. Node *L = NULL, Bst. Node *R = NULL) : data (d), left. Child (L), right. Child (R) { } ~Bst. Node ( ) { }

protected: Type data; Bst. Node<Type> *left. Child, *right. Child; }; template <class Type> class BST : public : Binary. Tree<Type> { private: Bst. Node<Type> *root; //二叉搜索树的根指针 Type Ref. Value; //数据输入停止的标志 Bst. Node<Type> *lastfound; //最近搜索到的结点的指针 void Make. Empty ( Bst. Node<Type> *& ptr );

void Insert ( const Type & x, Bst. Node<Type> *& ptr ); //插入 void Remove ( const Type & x, Bst. Node<Type> *& ptr ); //删除 void Print. Tree ( Bst. Node<Type> *ptr ) const; Bst. Node<Type> *Copy (const Bst. Node<Type> *ptr ); //复制 Bst. Node<Type> *Find (const Type & x, Bst. Node<Type> * ptr ) const; //搜索 Bst. Node<Type> *Min ( Bst. Node<Type> * ptr ) const; //求最小 Bst. Node<Type> *Max ( Bst. Node<Type> * ptr ) const; //求最大

friend class BSTIterator<Type>; //中序游标类 public: BST ( ) : root (NULL) { } BST ( Type value ) : Ref. Value (value), root (NULL) { } ~BST ( ); const BST & operator = ( const BST & Value ); void Make. Empty ( ) { Make. Empty ( ); root = NULL; } void Print. Tree ( ) const { Print. Tree ( root ); } int Find ( const Type & x ) const { return Find ( x, root ) != NULL; }

Type Min ( ) { return Min ( root )→data }; Type Max ( ) { return Max ( root )→data }; void Insert ( const Type & x ) { Insert ( x, root ); } void Remove ( const Type & x ) { Remove ( x, root ); } }


template <class Type> Bst. Node<Type> * BST<Type> : : Find (const Type & x, Bst. Node<Type> * ptr ) const { //二叉搜索树的递归的搜索算法 if ( ptr == NULL ) return NULL; //搜索失败 else if ( x < ptr→data ) //在左子树递归搜索 return Find ( x, ptr→left. Child ); else if ( x > ptr→data ) //在右子树递归搜索 return Find ( x, ptr→right. Child ); else return ptr; //相等, 搜索成功 }

template <class Type> Bst. Node <Type> * BST <Type> : : Find (const Type & x, Bst. Node<Type> * ptr ) const { //二叉搜索树的迭代的搜索算法 if ( ptr != NULL ) { Bst. Node<Type> * temp = ptr; while ( temp != NULL ) { if ( temp→data == x ) return temp; //成功 if ( temp→data < x ) temp = temp→right. Child; //右子树 else temp = temp→left. Child; //左子树 } } return NULL; //搜索失败 }



template <class Type> void BST<Type>: : Insert (const Type & x, Bst. Node<Type> * & ptr) { //递归的二叉搜索树插入算法 if ( ptr == NULL ) { //空二叉树 ptr = new Bst. Node<Type> (x); //创建含 x 结点 if ( ptr == NULL ) { cout << "Out of space" << endl; exit (1); } } else if ( x < ptr→data ) //在左子树插入 Insert ( x, ptr→left. Child ); else if ( x > ptr→data ) //在右子树插入 Insert ( x, ptr→right. Child ); }







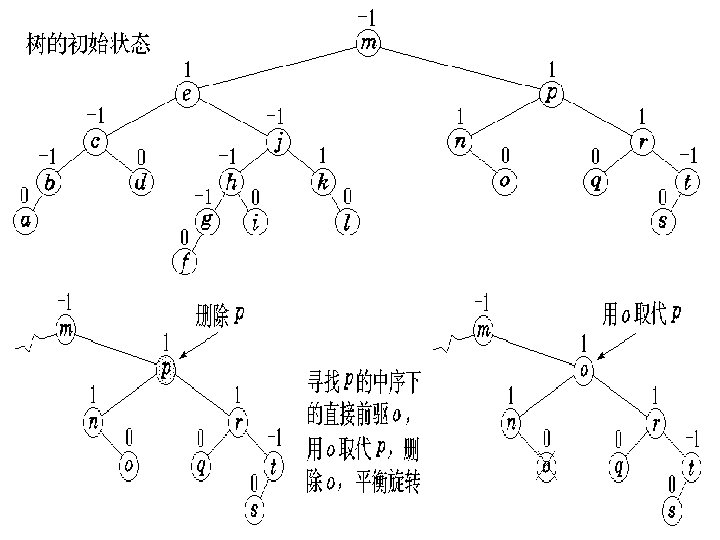
} else if ( ptr→left. Child != NULL && ptr→right. Child != NULL ) { temp = Min ( ptr→right. Child ); ptr→data = temp→data; Remove ( ptr→data, temp ); } else { temp = ptr; if ( ptr→left. Child == NULL ) ptr = ptr→right. Child; else if ( ptr→right. Child == NULL ) ptr = ptr→left. Child; delete temp; }

与二叉搜索树相关的中序游标类 二叉搜索树中序游标类的类定义 template <class Type> class Inorder. Iterator { public: Inorder. Iterator ( BST<Type> & Tree ) : ref (Tree) { Init ( ); } int Init ( ); //迭代栈初始化 int operator ! ( ); //判迭代栈空否 Type operator ( ); //取栈顶元素关键码 int operator ++ ( ); //按前序序列进栈, 遍历 private: BST<Type> & ref; //二叉搜索树对象 Stack < Bst. Node<Type> * > itr. Stack; //迭代栈 }
















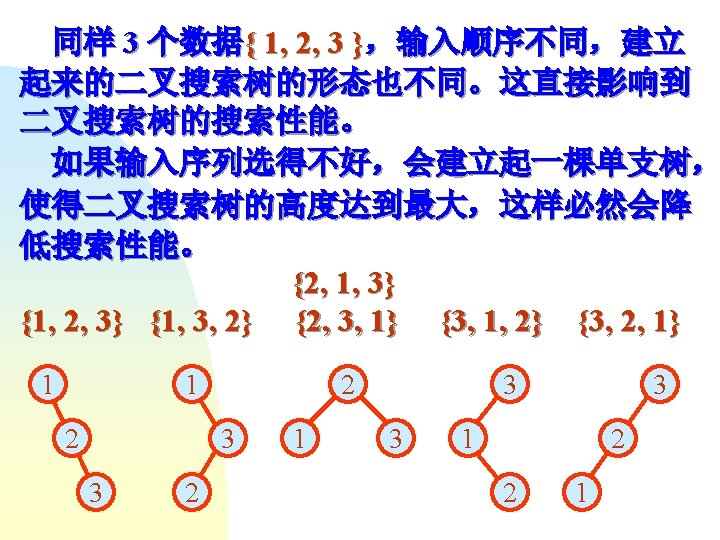
![第二步 C W R 左子树 右子树 115 90 1 T0 0 T1 2 165 第二步 C W R 左子树 右子树 115 90 1 T[0, 0] T[1, 2] 165](https://slidetodoc.com/presentation_image_h/fccdeb7a854d0a21b7ee6880e1dfb0f0/image-108.jpg)
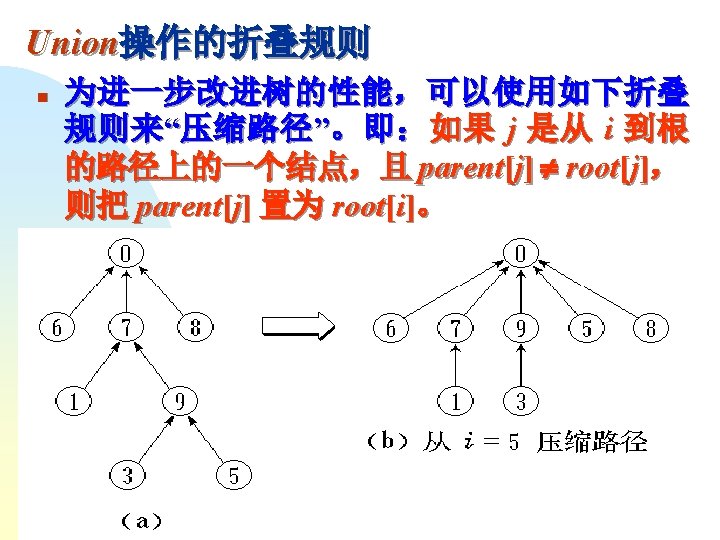
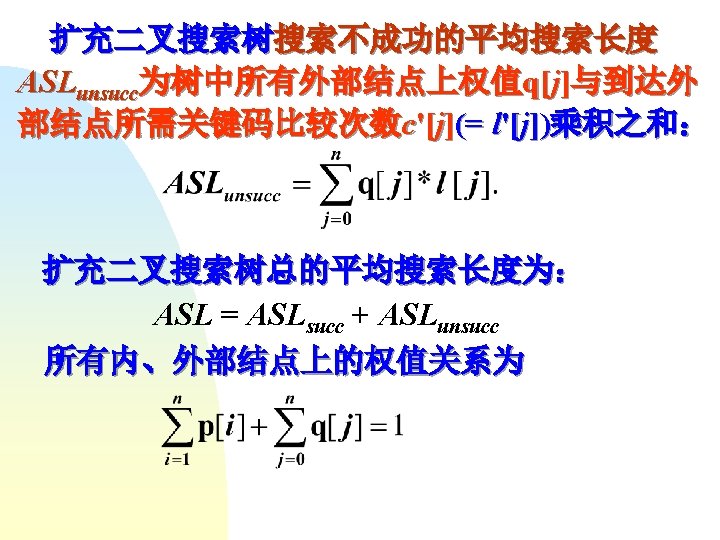
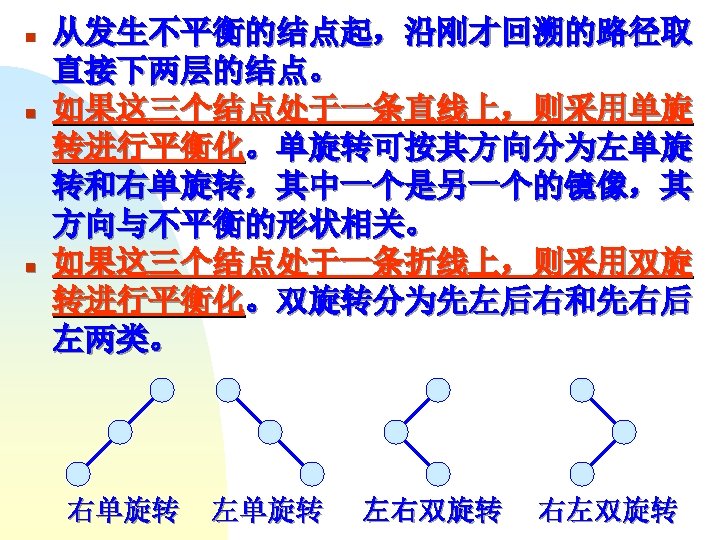
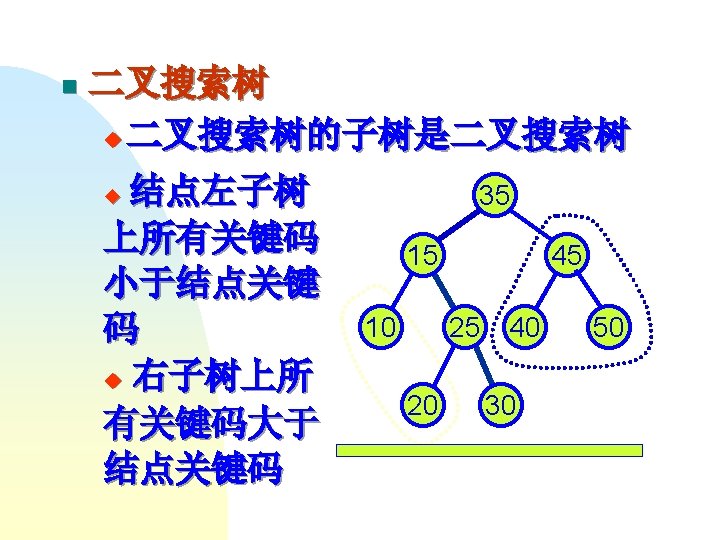
第二步 C W R 左子树 右子树 115 90 1 T[0, 0] T[1, 2] 165 90 2 T[0, 1] T[2, 2] 50 35 2 T[1, 1] T[2, 3] 60 35 3 T[1, 2] T[3, 3]
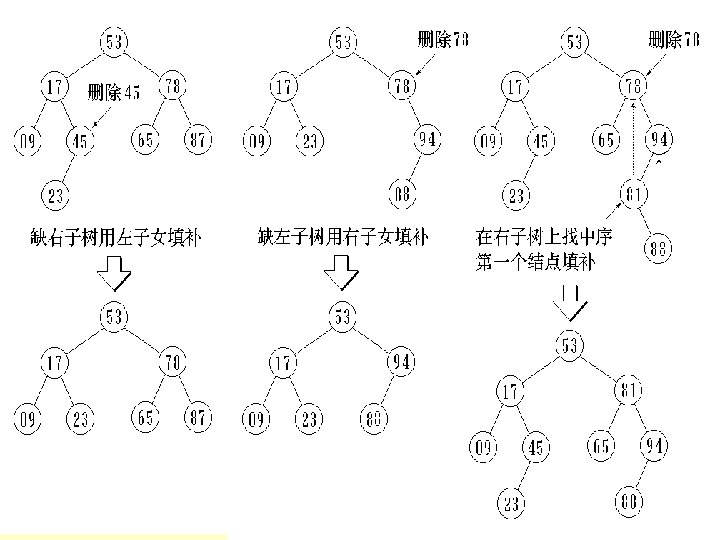
![第三步 C W R 左子树 右子树 150 100 1 T0 0 T1 3 190 第三步 C W R 左子树 右子树 150 100 1 T[0, 0] T[1, 3] 190](https://slidetodoc.com/presentation_image_h/fccdeb7a854d0a21b7ee6880e1dfb0f0/image-109.jpg)
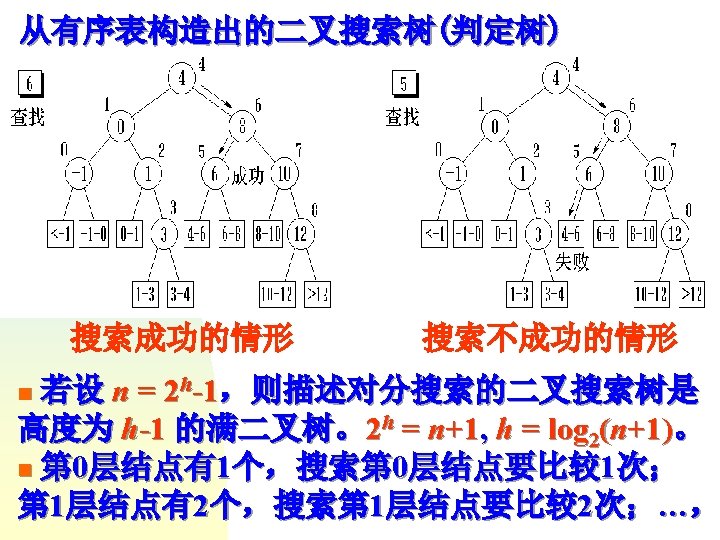
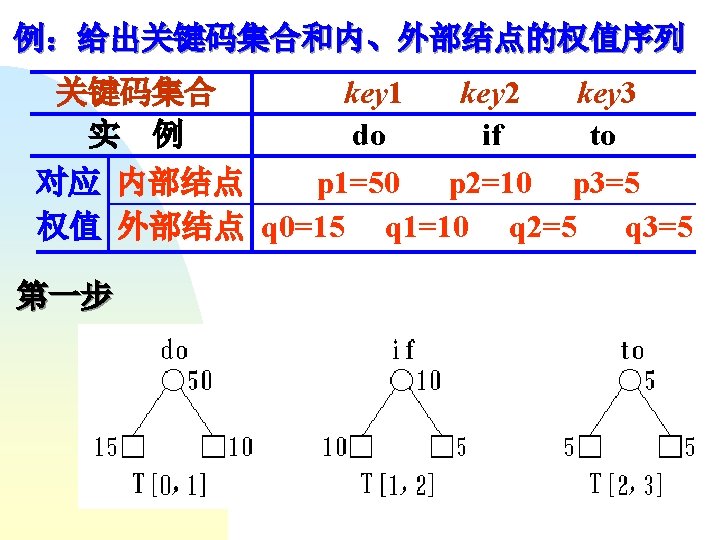
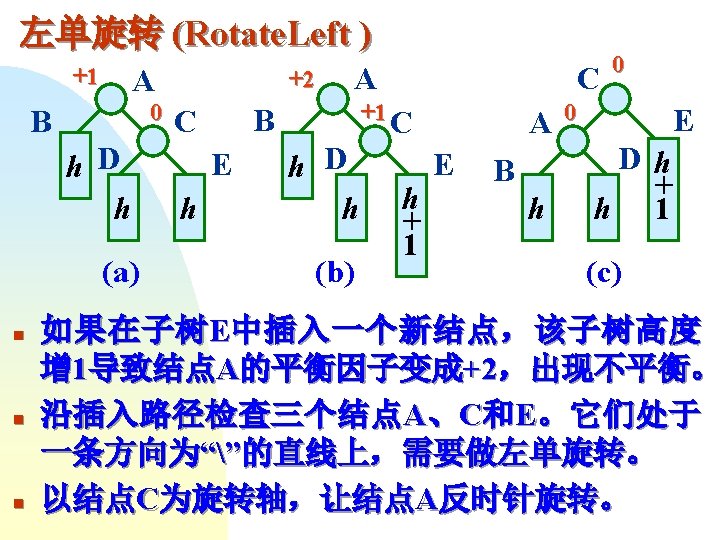
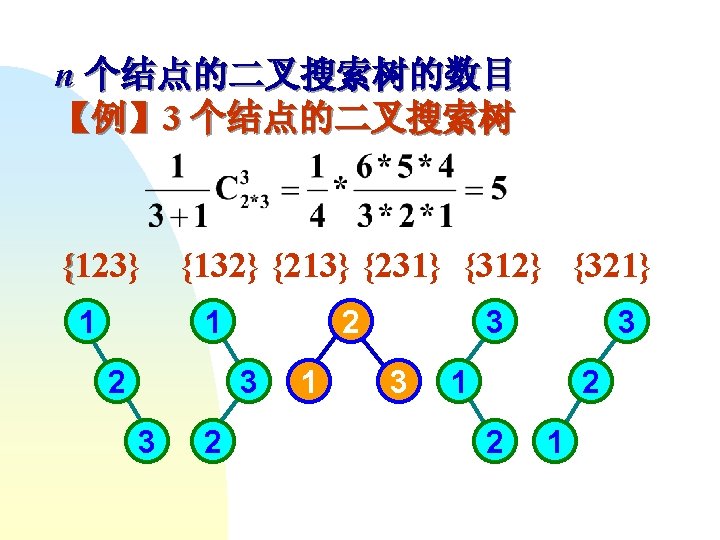
第三步 C W R 左子树 右子树 150 100 1 T[0, 0] T[1, 3] 190 100 2 T[0, 1] T[2, 3] 215 100 3 T[0, 2] T[3, 3]

0 1 2 3 0 15 75 90 100 1 10 25 35 2 5 15 3 5 W[i][j] 0 0 0 1 2 3 1 1 0 R[i][j] 2 1 2 0 3 1 2 3 0 0 75 115 150 1 0 25 50 2 0 15 3 0 C[i][j] 3个关键码 { do, if, to } 的 最优二叉搜索树 p 1=50, p 2=10, p 3=5 q 0=15, q 1=10, q 2= 5, q 3= 5



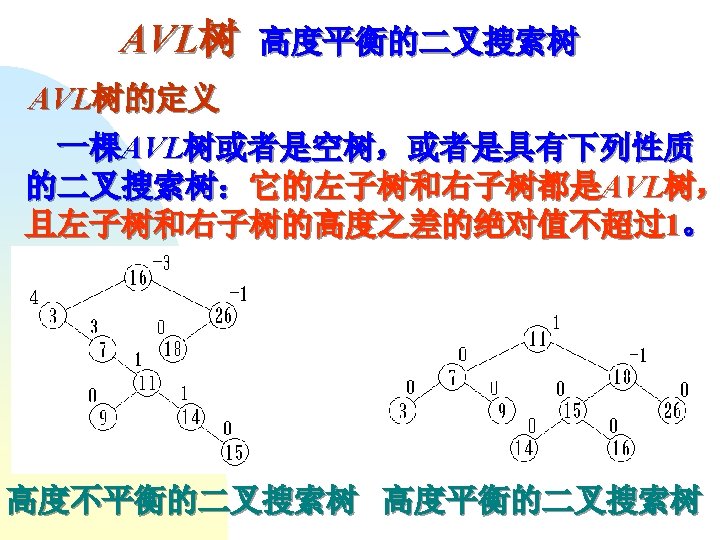
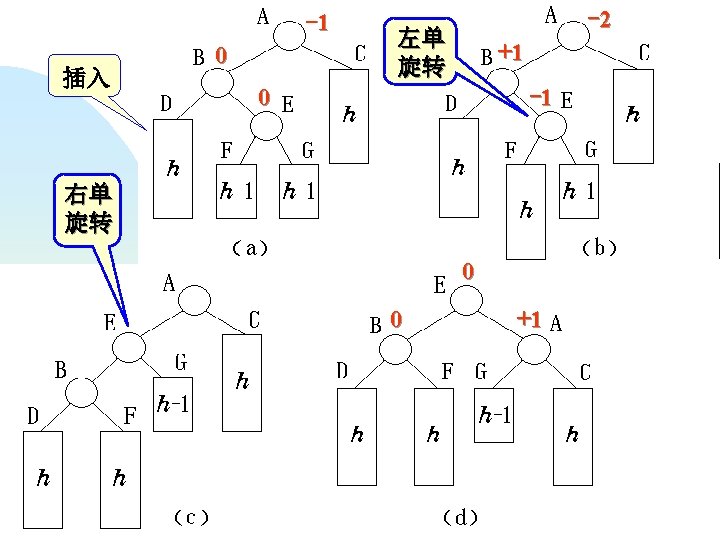
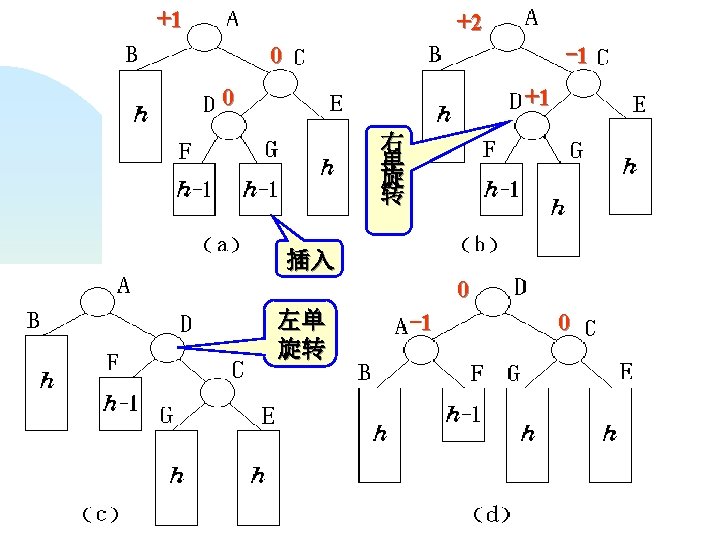
AVL树的类定义 template <class Type> class AVLTree { public: struct AVLNode { Type data; AVLNode *left, *right; int balance; AVLNode ( ) : left (NULL), right (NULL), balance (0) { } AVLNode ( Type d, AVLNode<Type> *l = NULL, AVLNode<Type> *r = NULL ) : data (d), left (l), right (r), balance (0) { } };

protected: Type Ref. Value; AVLNode *root; int Insert ( AVLNode<Type>* &tree, Type x, int &taller ); void Rotate. Left ( AVLNode<Type> *Tree, AVLNode<Type> * &New. Tree ); void Rotate. Right ( AVLNode<Type> *Tree, AVLNode<Type> * &New. Tree ); void Left. Balance ( AVLNode<Type> * &Tree, int &taller ); void Right. Balance ( AVLNode<Type> * &Tree, int &taller );

int Depth ( AVLNode<Type> *t ) const; public: AVLTree ( ) : root (NULL) { } AVLNode ( Type Ref ) : Ref. Value (Ref), root (NULL) { } int Insert ( Type x ) { int taller; return Insert ( root, x, taller ); } friend istream& operator >> ( istream& in, AVLTree<Type>& Tree ); friend ostream& operator << ( ostream& out, const AVLTree<Type>& Tree ); int Depth ( ) const; }




template <class Type> void AVLTree<Type> : : Rotate. Left ( AVLNode<Type> *Tree, AVLNode<Type> * &New. Tree ) { //左单旋转的算法 New. Tree = Tree→right; Tree→right = New. Tree→left; New. Tree→left = Tree; }


template <class Type> void AVLTree<Type>: : Rotate. Right ( AVLNode<Type> *Tree, AVLNode<Type> * &New. Tree) { //右单旋转的算法 New. Tree = Tree→left; Tree→left = New. Tree→right; New. Tree→right = Tree; }



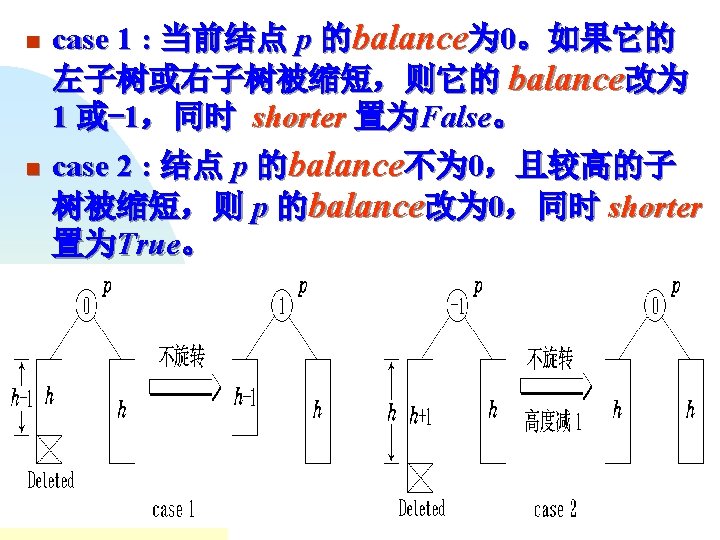
template <class Type> void AVLTree<Type>: : Left. Balance ( AVLNode<Type> * &Tree, int & taller ) { //左平衡化的算法 AVLNode<Type> *leftsub = Tree→left, *rightsub; switch ( leftsub→balance ) { case -1 : Tree→balance = leftsub→balance = 0; Rotate. Right ( Tree, Tree ); taller = 0; break; case 0 : cout << “树已经平衡化. n"; break; 树已经平衡化

case 1 : rightsub = leftsub→right; switch ( rightsub→balance ) { case -1: Tree→balance = 1; leftsub→balance = 0; break; case 0 : Tree→balance = leftsub→balance = 0; break; case 1 : Tree→balance = 0; leftsub→balance = -1; break; }

rightsub→balance = 0; Rotate. Left ( leftsub, Tree→left ); Rotate. Right ( Tree, Tree ); taller = 0; } }



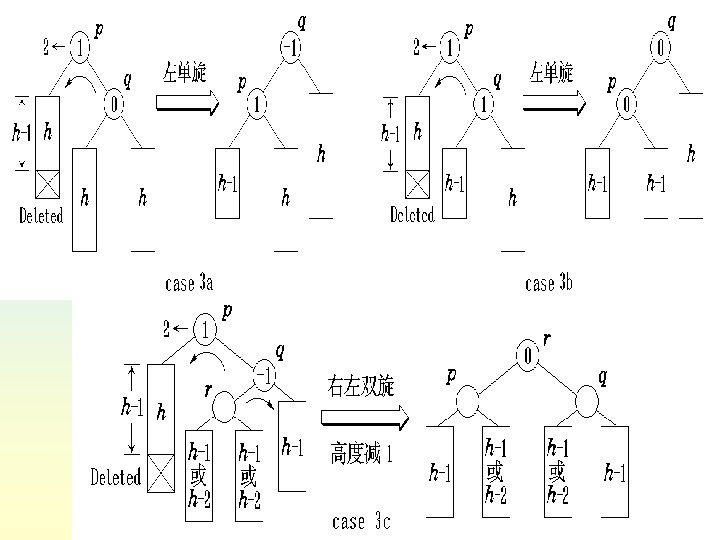
template <class Type> void AVLTree<Type>: : Right. Balance ( AVLNode<Type> * &Tree, int & taller ) { //右平衡化的算法 AVLNode<Type> *rightsub = Tree→right, *leftsub; switch ( rightsub→balance ) { case 1 : Tree→balance = rightsub→balance = 0; Rotate. Left ( Tree, Tree ); taller = 0; break; case 0 : cout << “树已经平衡化. n"; break; 树已经平衡化 case -1 : leftsub = rightsub→left;

switch ( leftsub→balance ) { case 1 : Tree→balance = -1; rightsub→balance = 0; break; case 0 : Tree→balance = rightsub→balance = 0; break; case -1 : Tree→balance = 0; rightsub→balance = 1; break; } leftsub→balance = 0; Rotate. Right ( rightsub, Tree→left ); Rotate. Left ( Tree, Tree ); taller = 0; } }


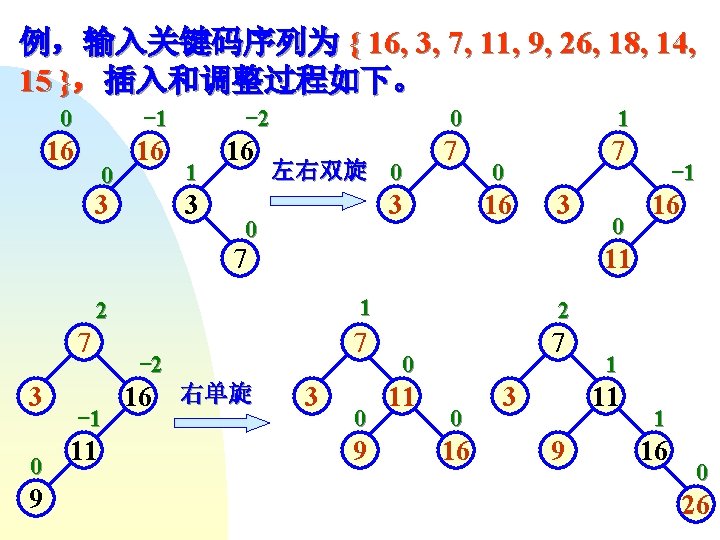
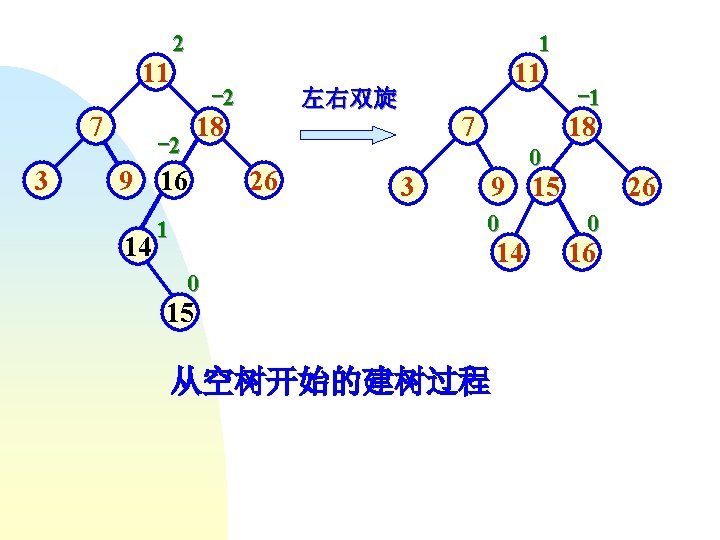
例,输入关键码序列为 { 16, 3, 7, 11, 9, 26, 18, 14, 15 },插入和调整过程如下。 0 -1 16 16 0 3 -2 1 3 16 左右双旋 0 0 1 7 7 3 0 0 16 3 7 3 0 9 -1 11 -2 16 右单旋 16 11 2 7 0 -1 3 1 2 7 7 0 9 0 11 0 16 3 1 11 9 1 16 0 26

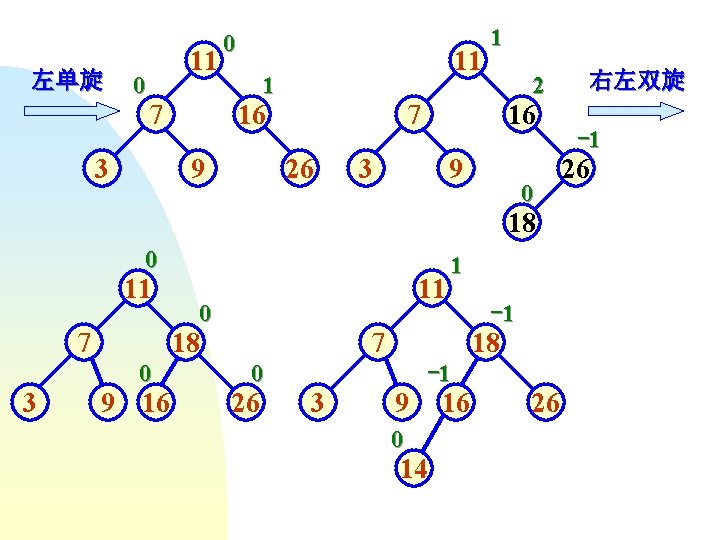
左单旋 11 0 7 3 0 11 1 16 9 1 2 7 26 16 3 9 0 18 0 11 7 0 18 0 3 11 9 16 1 7 18 0 26 -1 -1 3 9 0 14 16 26 右左双旋 -1 26

2 1 11 7 3 -2 左右双旋 18 -2 9 16 14 11 7 26 18 0 3 9 15 0 1 -1 14 0 15 从空树开始的建树过程 26 0 16

} } case -1 : tree→balance = 0; taller = 0; break; case 0 : tree→balance = 1; break; case 1 : Right. Balance ( tree, taller ); break; } return success;















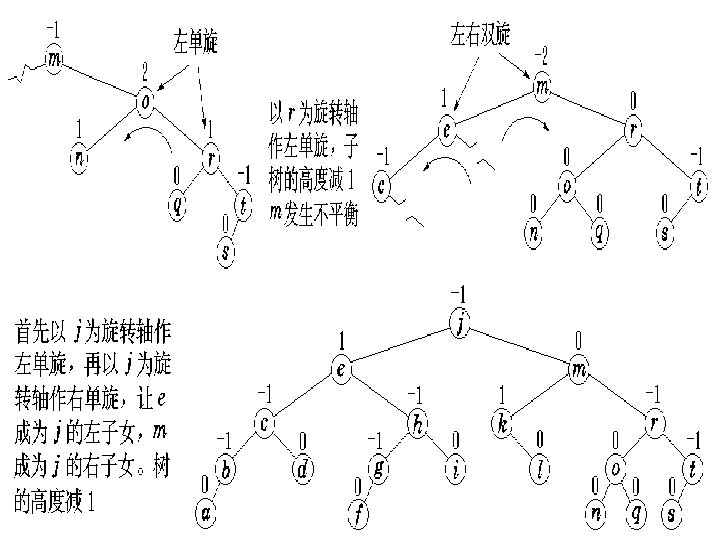
% 并查集操作的算法 n 查找 0 -5 1 0 2 1 3 2 4 3 Find (4) Find (3) =3 Find (2) =2 Find (1) =1 Find (0) = 0 = -5 < 0 结束
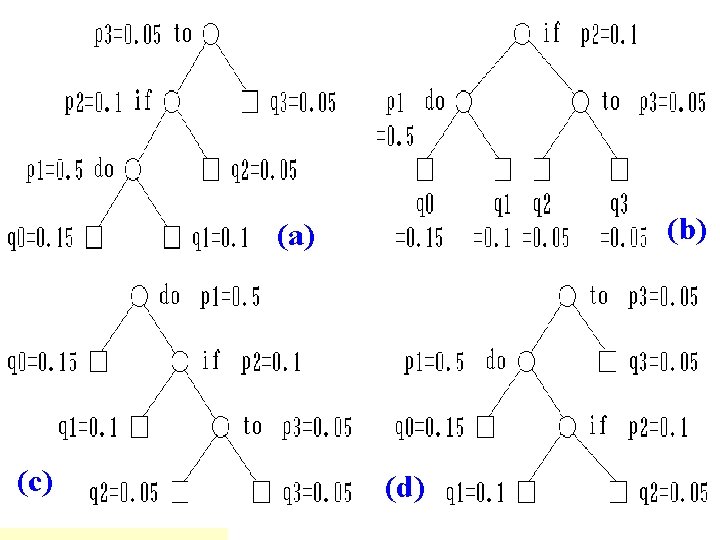
![0 parent 5 1 2 0 3 1 4 2 3 Parent0 Parent4 Parent1 0 parent -5 1 2 0 3 1 4 2 3 Parent[0] Parent[4] Parent[1]](https://slidetodoc.com/presentation_image_h/fccdeb7a854d0a21b7ee6880e1dfb0f0/image-151.jpg)
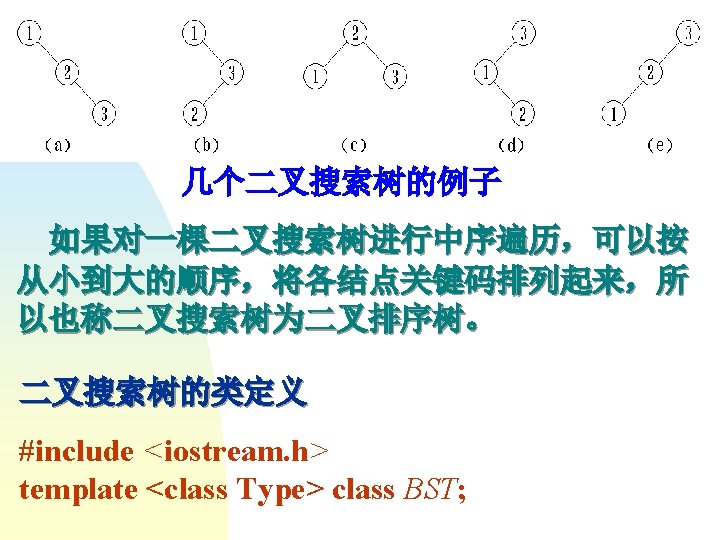
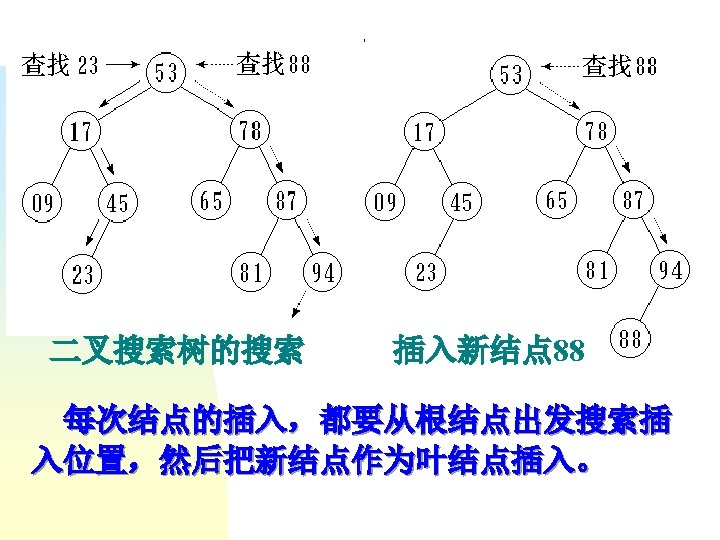
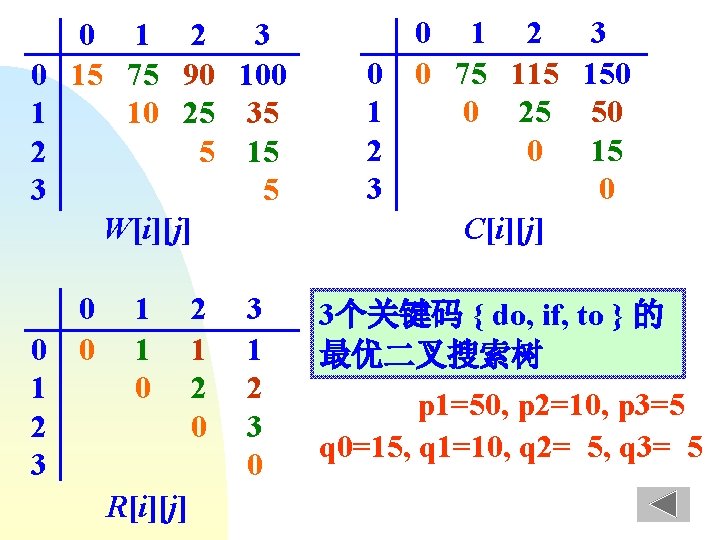
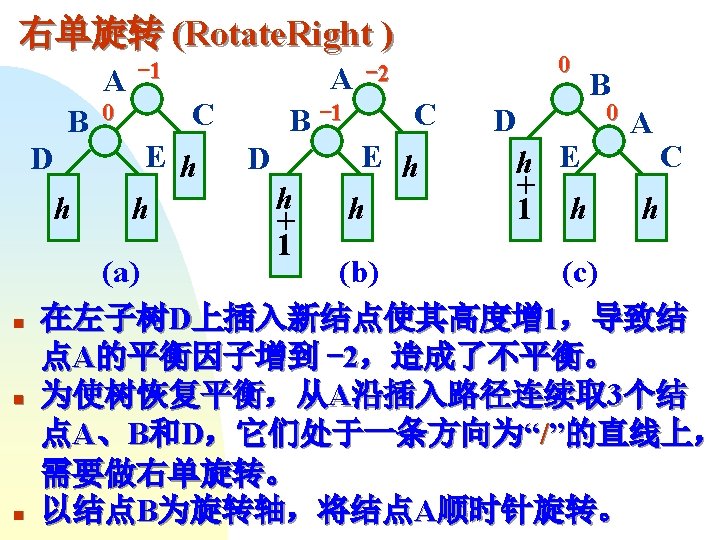
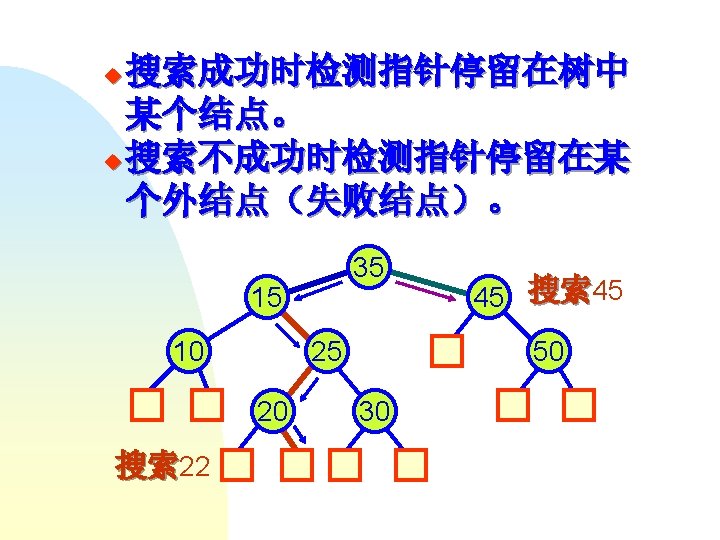
0 parent -5 1 2 0 3 1 4 2 3 Parent[0] Parent[4] Parent[1] Parent[3] =3 =-5 =0 Parent[2] =2 =1 int Find ( int x ) { if ( parent [x] < 0 ) return x; else return Find ( parent [x] ); }

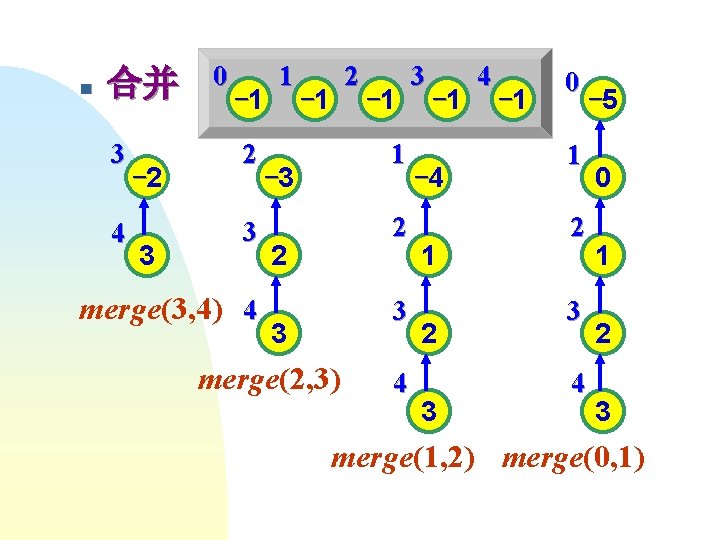
n 合并 3 4 -2 3 0 -1 2 3 merge(3, 4) 4 1 2 -1 -1 1 -3 2 2 3 3 merge(2, 3) 4 3 -1 -4 1 2 3 4 -1 0 1 2 3 4 -5 0 1 2 3 merge(1, 2) merge(0, 1)










