Venn diagrams sets vectors and functions Revision Vectors













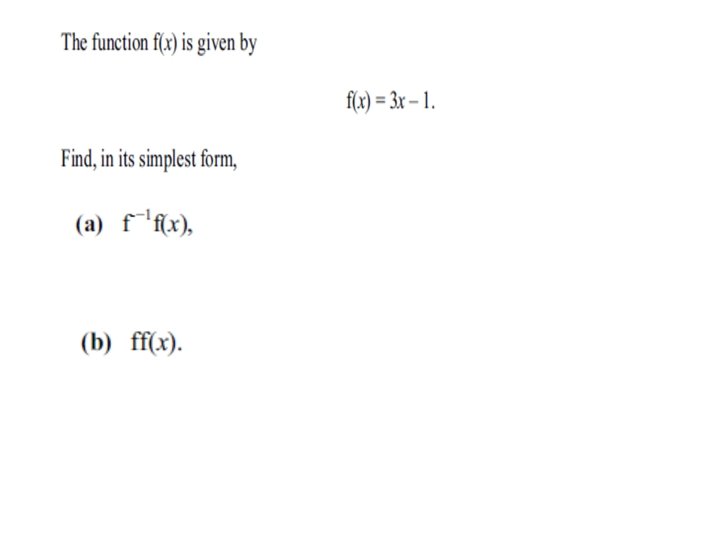
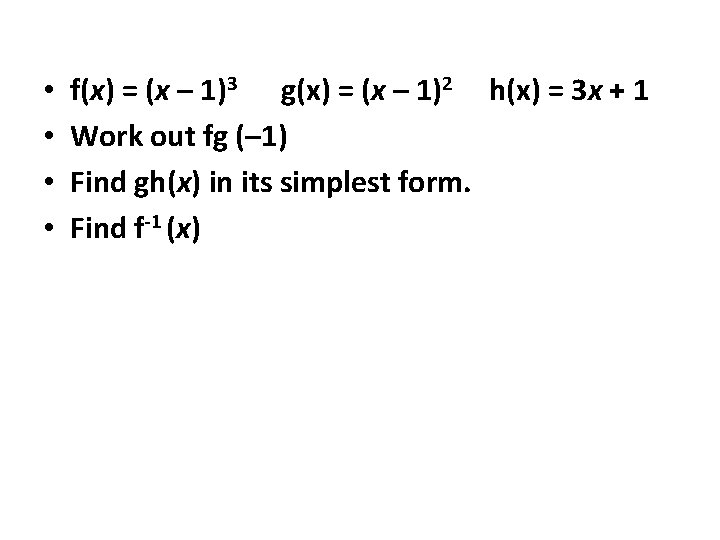
- Slides: 34

Venn diagrams, sets, vectors and functions. Revision

Vectors 1 2 video vid 2 Vid 3 Sets 1 2 Vid 1 Functions 1 Vid 1 vid 2

You should be able to; 1. Use language, notation and Venn diagrams to describe sets and represent relationships between sets 2. Write a vector using correct notation, make calculations with vectors, and find its resultant, modulus and representations in terms of a vector. 3. To learn the vocabulary relating to functions. To learn the different types of functions. To practice defining functions and finding composite functions

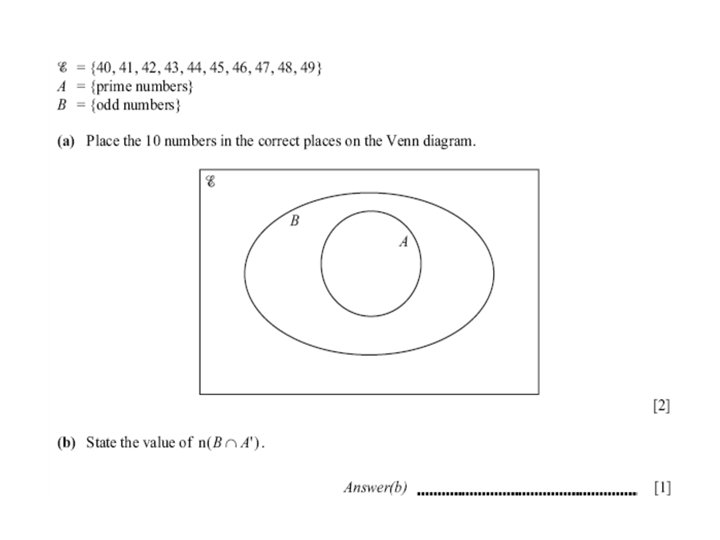
Set Notation • Number of elements in set A • “…is an element of …” • “…is not an element of…” • Complement of set A A' • The empty set ∅ • Universal set ξ • A is a subset of B • A is a proper subset of B • A is not a subset of B A⊄ B • Union of A and B AUB • Intersection of A and B A∩B n(A)

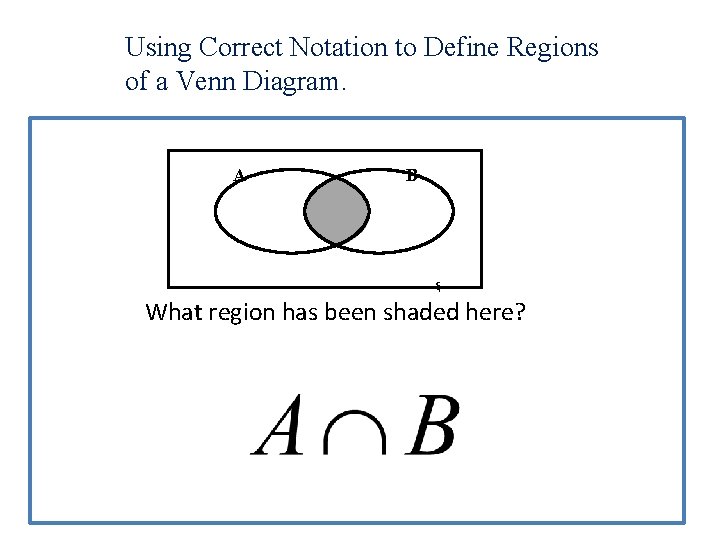
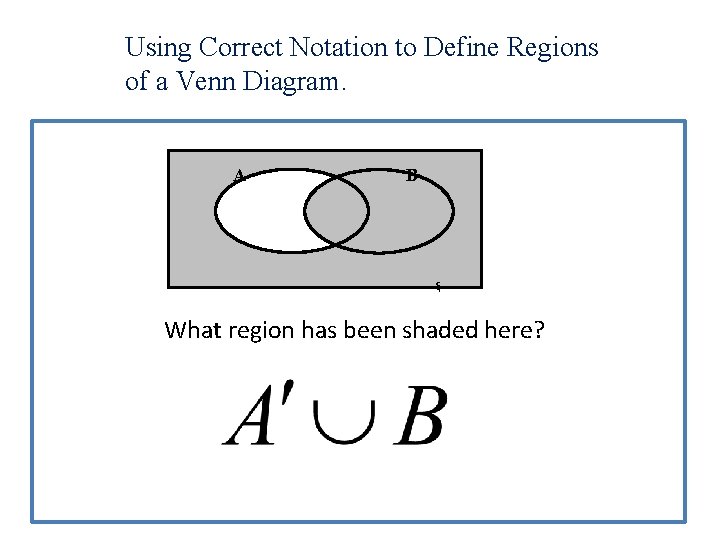
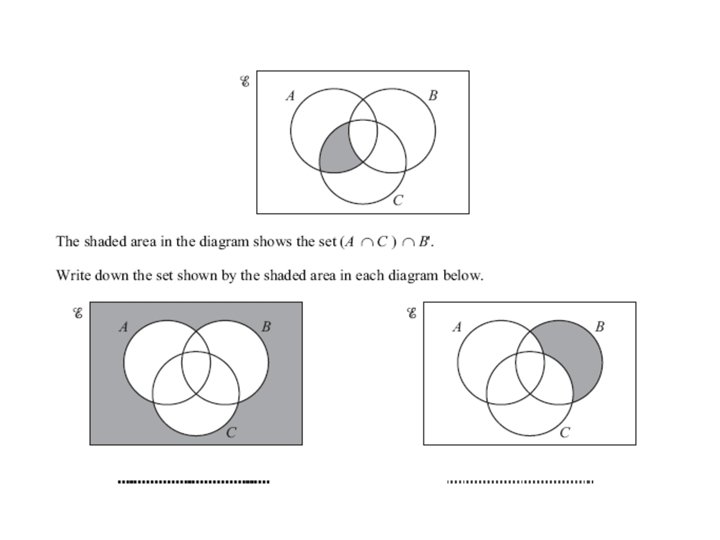
Using Correct Notation to Define Regions of a Venn Diagram. A B ξ What region has been shaded here?

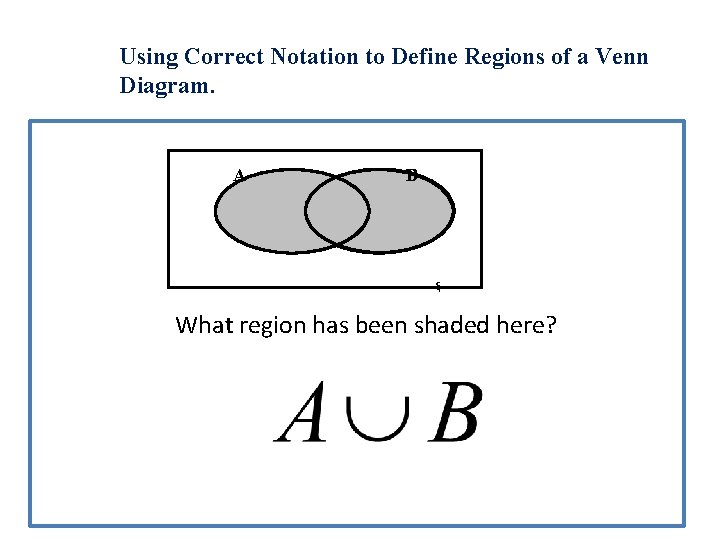
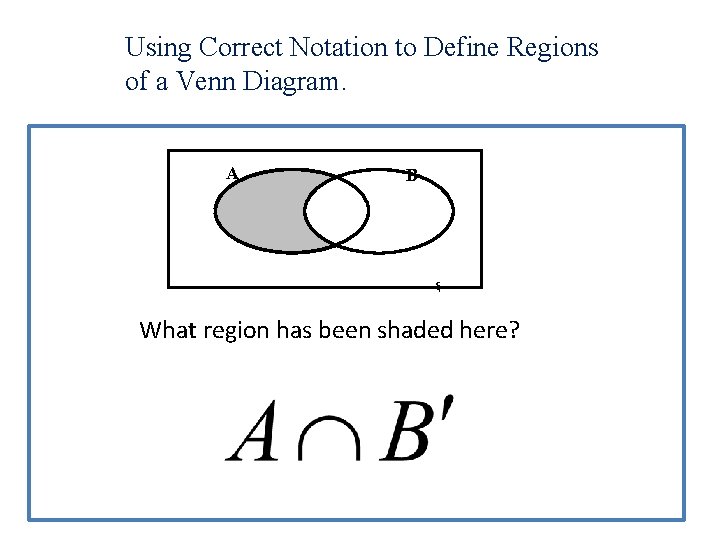
Using Correct Notation to Define Regions of a Venn Diagram. A B ξ What region has been shaded here?

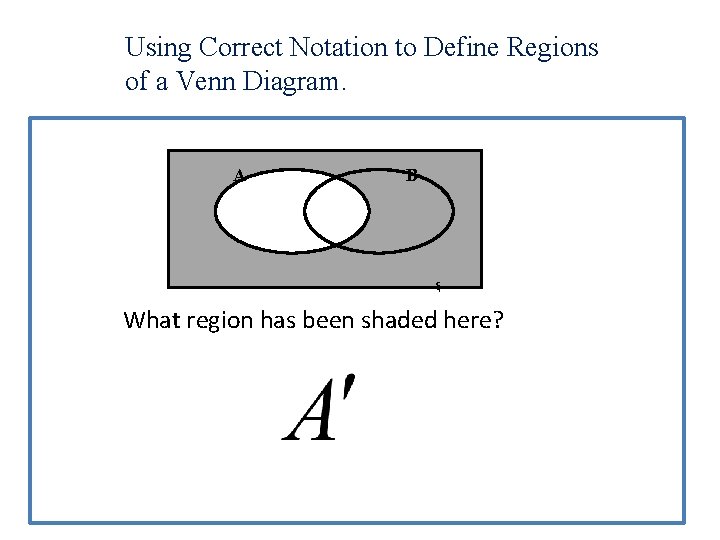
Using Correct Notation to Define Regions of a Venn Diagram. A B ξ What region has been shaded here?

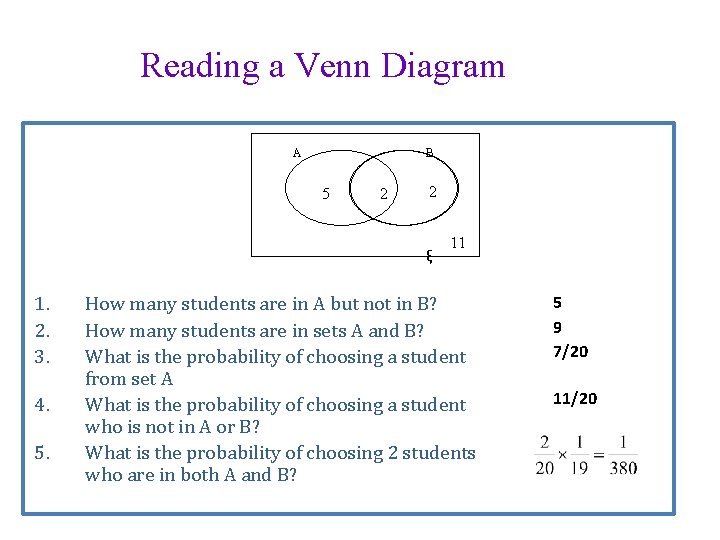
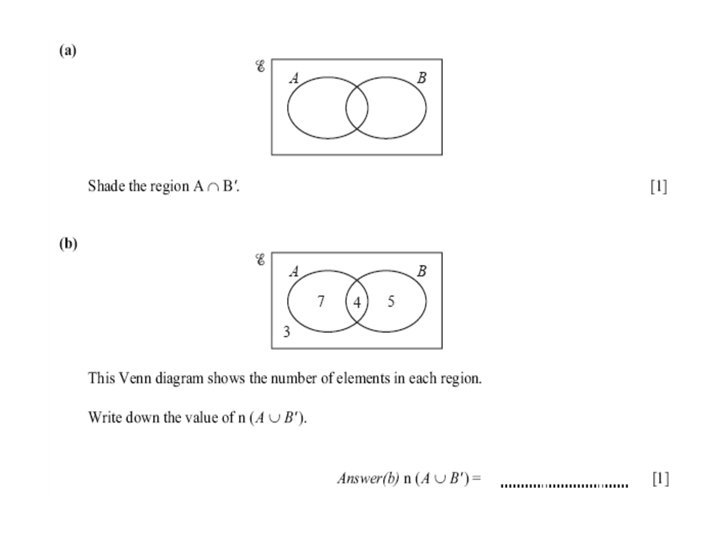
Reading a Venn Diagram A B 5 2 2 ξ 1. 2. 3. 4. 5. 11 How many students are in A but not in B? How many students are in sets A and B? What is the probability of choosing a student from set A What is the probability of choosing a student who is not in A or B? What is the probability of choosing 2 students who are in both A and B? 5 9 7/20 11/20

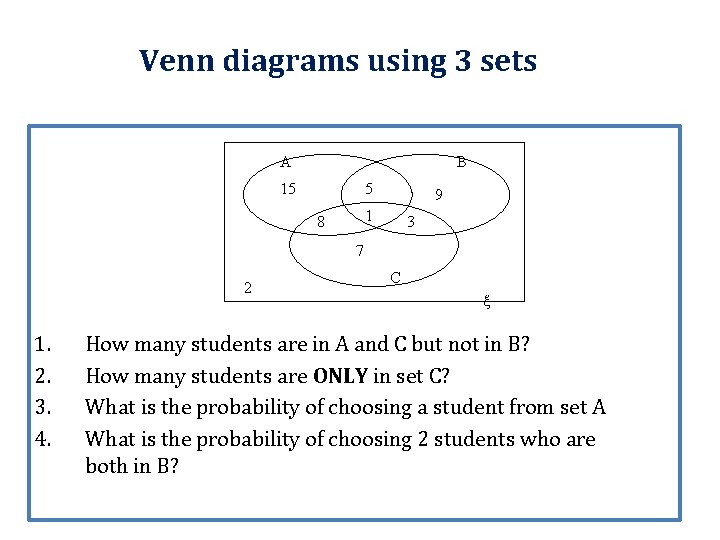
Venn diagrams using 3 sets A B 15 5 9 1 8 3 7 2 1. 2. 3. 4. C ξ How many students are in A and C but not in B? How many students are ONLY in set C? What is the probability of choosing a student from set A What is the probability of choosing 2 students who are both in B?

Using Correct Notation to Define Regions of a Venn Diagram. A B ξ What region has been shaded here?

Using Correct Notation to Define Regions of a Venn Diagram. A B ξ What region has been shaded here?





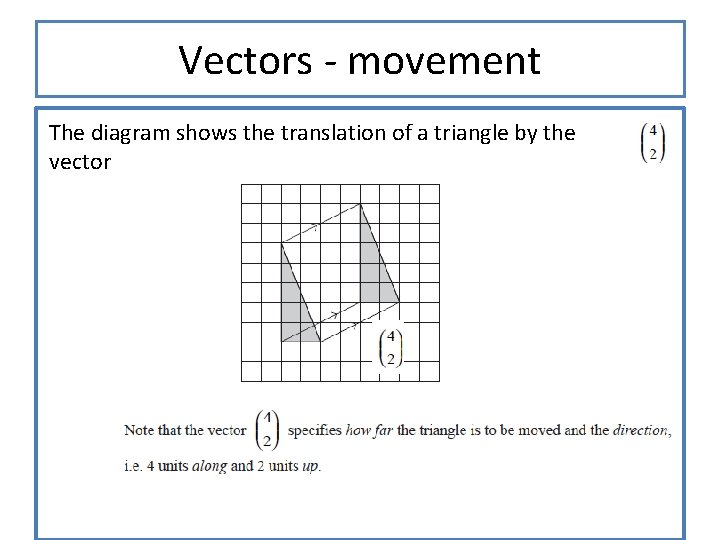
Vectors - movement The diagram shows the translation of a triangle by the vector

Vector displacement

Adding vectors

What do we mean by 6 a? • 6 a means 6 lots of vector a • So if a = then 6 a =

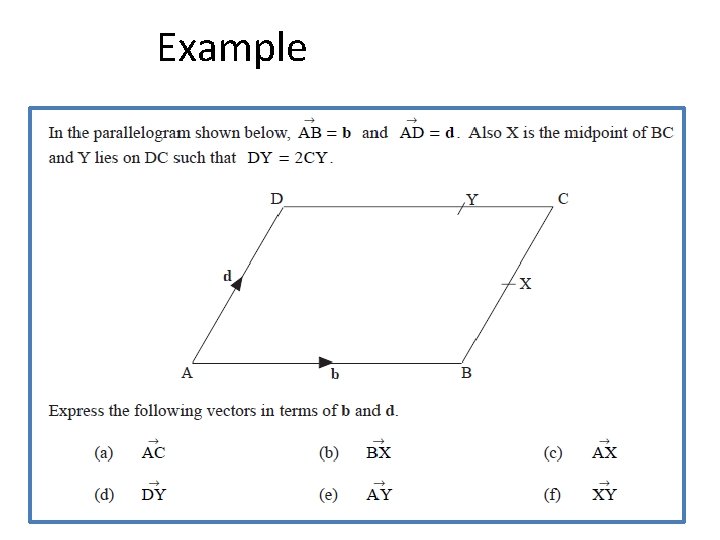
Example

Example

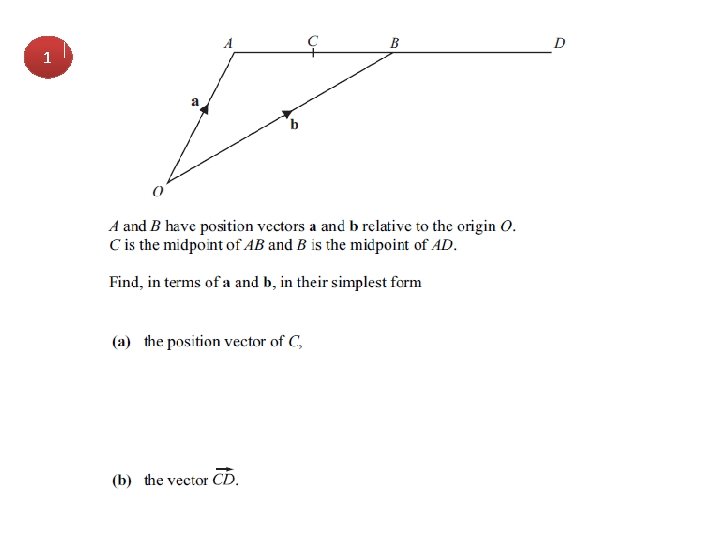
1

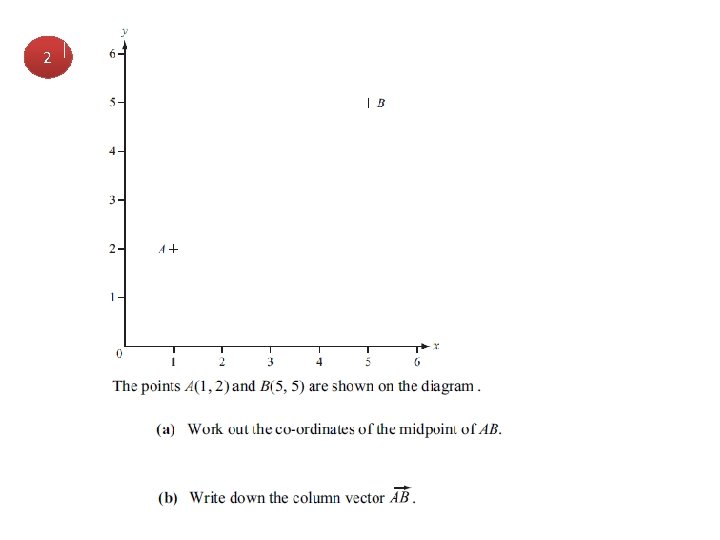
2

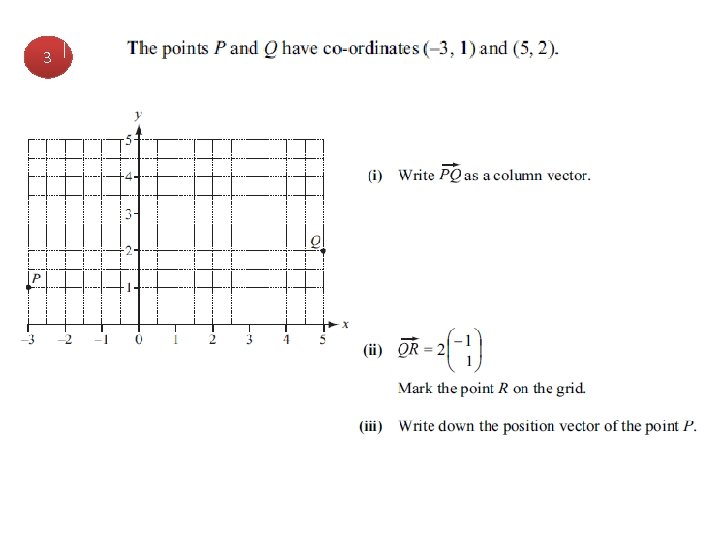
3

4

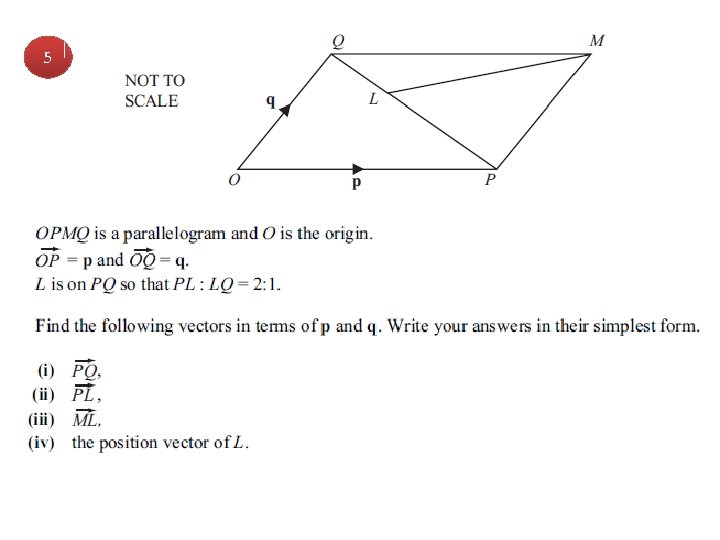
5

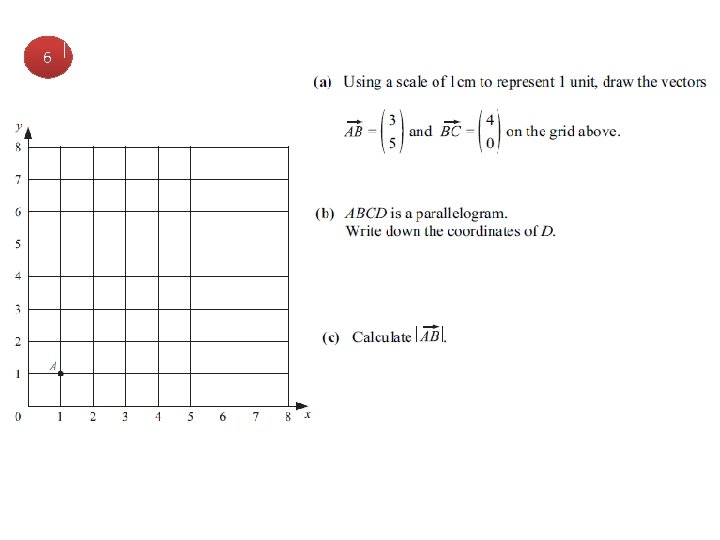
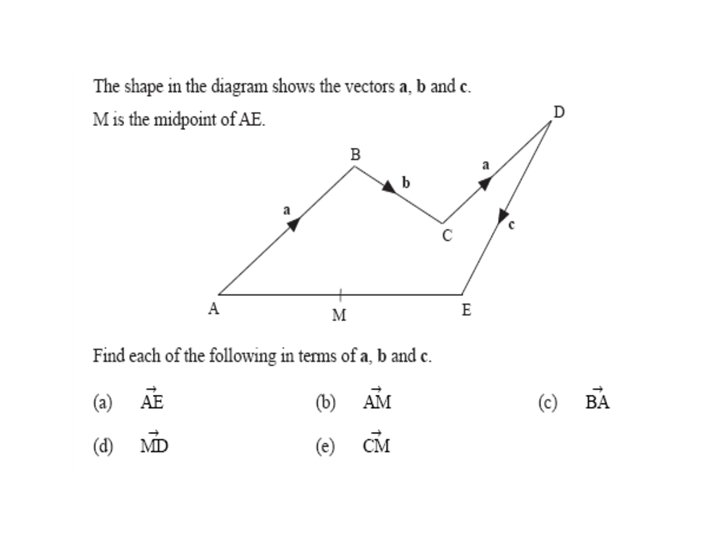
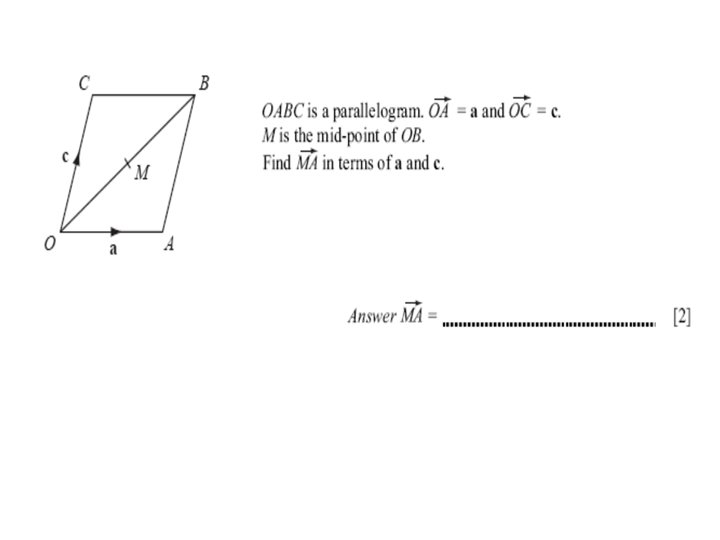
6



Substituting numbers into functions A function can be written as: Try some of these: Substituting is replacing the x so that, a) f(1)= 2 b) f(-2)= 12 a) g(3)= 2 b) g(-1)= 6 a) h(1)= 27 b) h(-5)= 3 Check these mentally: 4 3– 3=9 4 0 – 3 = – 3 4 (– 2) – 3 = – 11

Composite functions A composite function is made up of two or more functions. Try some of these: fg(x) means take g(x) and put it into f(x). Replace each x in f(x) with the complete g(x). 3 x² + 8 9 x² - 6 x + 4 gf(x) means take f(x) and put it into g(x). Replace each x in g(x) with the complete f(x). x+1 √(3 x – 3)

Inverse Functions Another way to do the Inverse Functions is to consider what they do. The INVERSE function finds the input for a given output. So if f(x) = 5 x – 7 y = 5 x – 7 We now need to make x the subject…. So x = (y + 7)/5 The inverse function is written as: f – 1(x) = (x + 7)/5
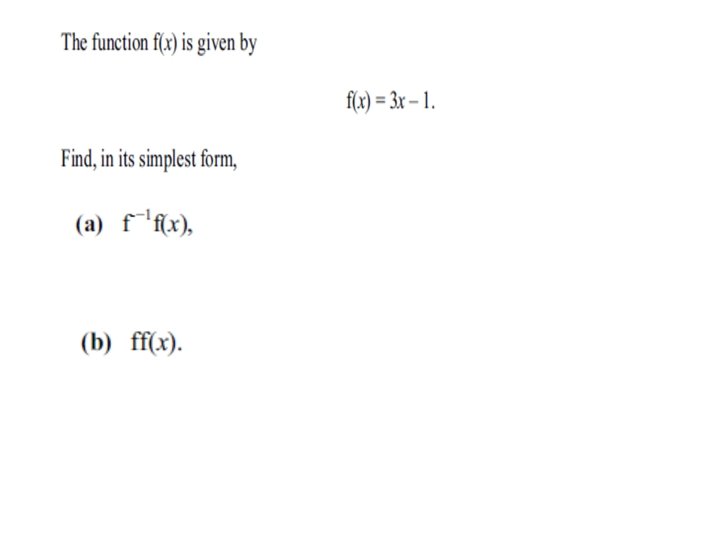
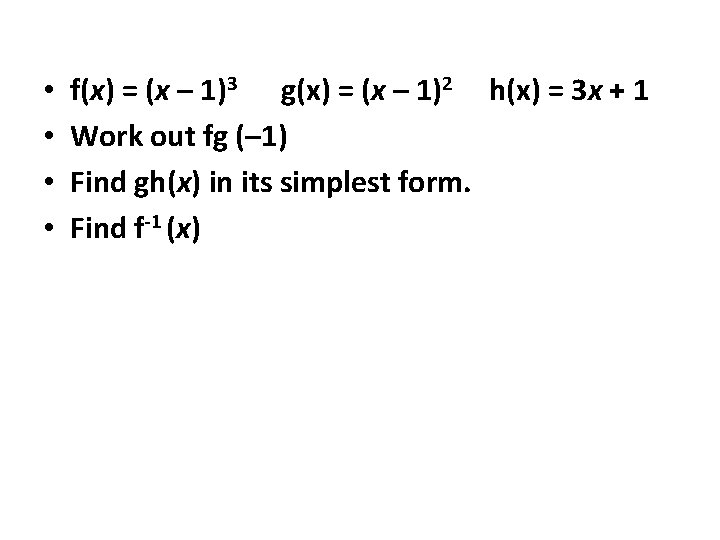
• • f(x) = (x – 1)3 g(x) = (x – 1)2 h(x) = 3 x + 1 Work out fg (– 1) Find gh(x) in its simplest form. Find f-1 (x)