Venn Diagrams Notation Demonstration This resource provides animated

Venn Diagrams – Notation – Demonstration This resource provides animated demonstrations of the mathematical method. Check animations and delete slides not needed for your class.

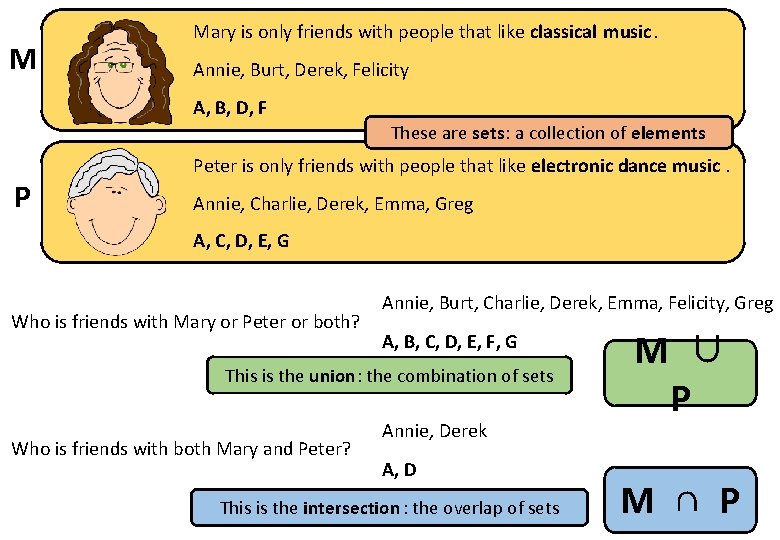
M Mary is only friends with people that like classical music. Annie, Burt, Derek, Felicity A, B, D, F These are sets: a collection of elements P Peter is only friends with people that like electronic dance music. Annie, Charlie, Derek, Emma, Greg A, C, D, E, G Who is friends with Mary or Peter or both? Annie, Burt, Charlie, Derek, Emma, Felicity, Greg A, B, C, D, E, F, G This is the union: the combination of sets Who is friends with both Mary and Peter? Annie, Derek A, D This is the intersection : the overlap of sets M ∪ P M ∩ P

Set Notation Universal Sets of Data ξ = {Numbers 1 to 20 inclusive} Elements A = {Square Numbers} = {1, 4, 9, 16} What is… B = {Multiples of 4} = {4, 8, 12, 16, 20} A ∪ B Union: the combination of A and B. A ∪ B = {1, 4, 8, 9, 12, 16, 20} A ∩ B Intersection : The overlap of A and B. A ∩ B = {4, 16} A’ Complement : Not in A. A’ = {2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20}

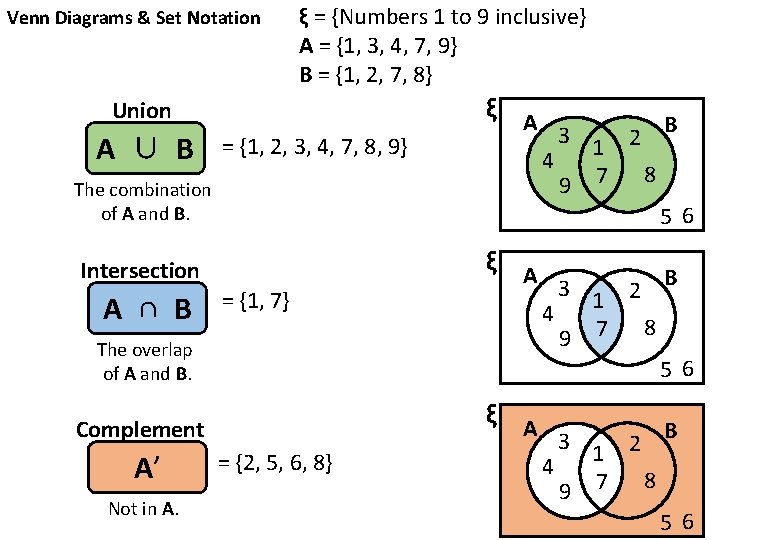
Venn Diagrams & Set Notation ξ = {Numbers 1 to 9 inclusive} A = {1, 3, 4, 7, 9} B = {1, 2, 7, 8} Union A ∪ B = {1, 2, 3, 4, 7, 8, 9} 9 The combination of A and B. = {1, 7} 7 8 5 6 Complement Not in A. 8 ξ A 3 1 2 B 4 9 The overlap of A and B. A’ 7 5 6 Intersection A ∩ B ξ A 3 1 2 B 4 = {2, 5, 6, 8} ξ A 3 1 2 B 4 9 7 8 5 6

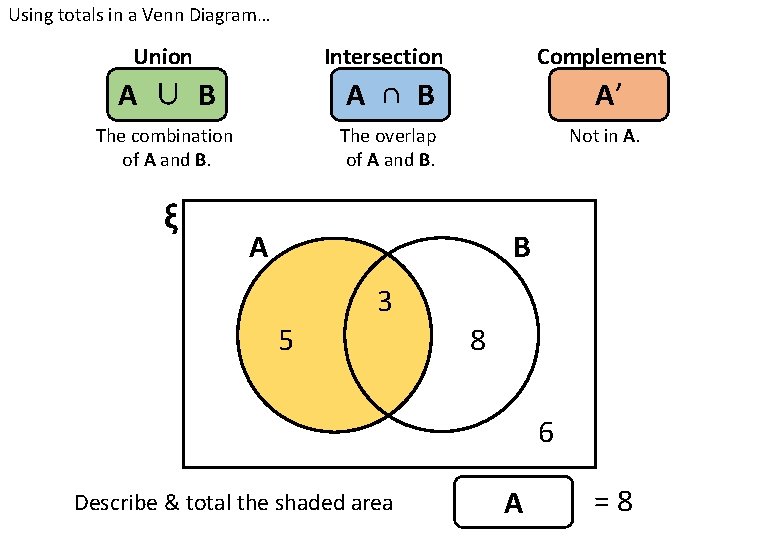
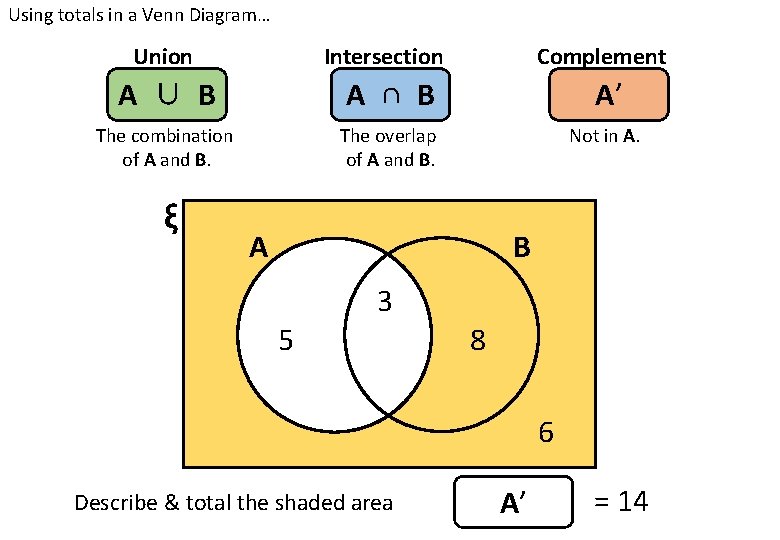
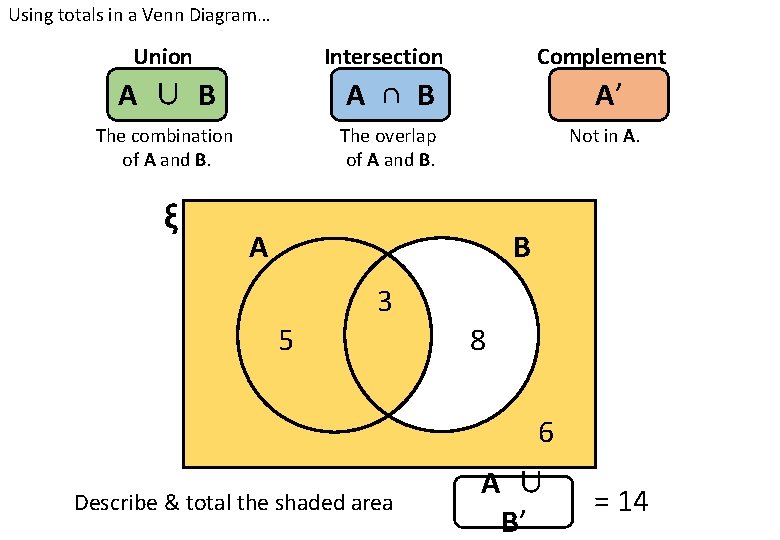
Using totals in a Venn Diagram… Union Intersection Complement A ∪ B A ∩ B A’ The combination of A and B. The overlap of A and B. Not in A. ξ A B 3 5 8 6 Describe & total the shaded area A =8

Using totals in a Venn Diagram… Union Intersection Complement A ∪ B A ∩ B A’ The combination of A and B. The overlap of A and B. Not in A. ξ A B 3 5 8 6 Describe & total the shaded area A’ = 14

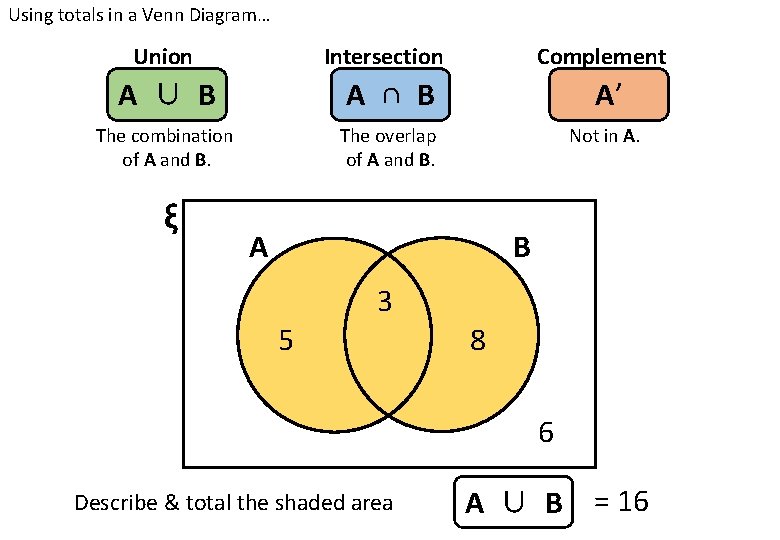
Using totals in a Venn Diagram… Union Intersection Complement A ∪ B A ∩ B A’ The combination of A and B. The overlap of A and B. Not in A. ξ A B 3 5 8 6 Describe & total the shaded area A ∪ B = 16

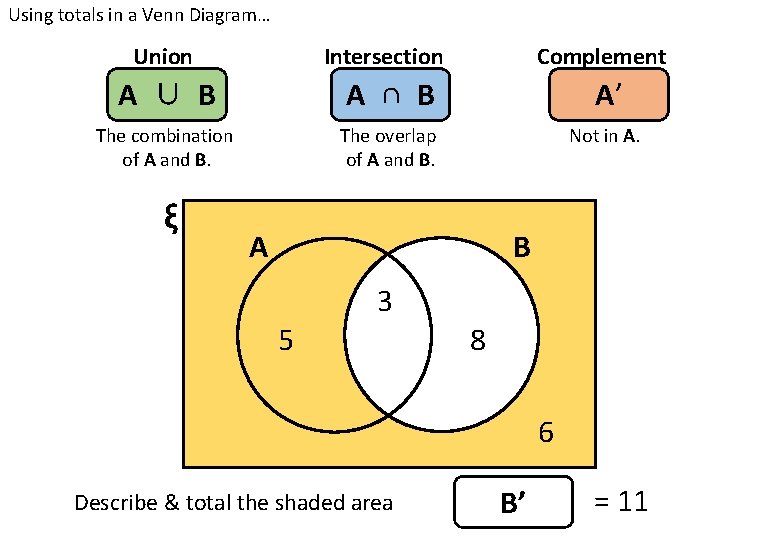
Using totals in a Venn Diagram… Union Intersection Complement A ∪ B A ∩ B A’ The combination of A and B. The overlap of A and B. Not in A. ξ A B 3 5 8 6 Describe & total the shaded area B’ = 11

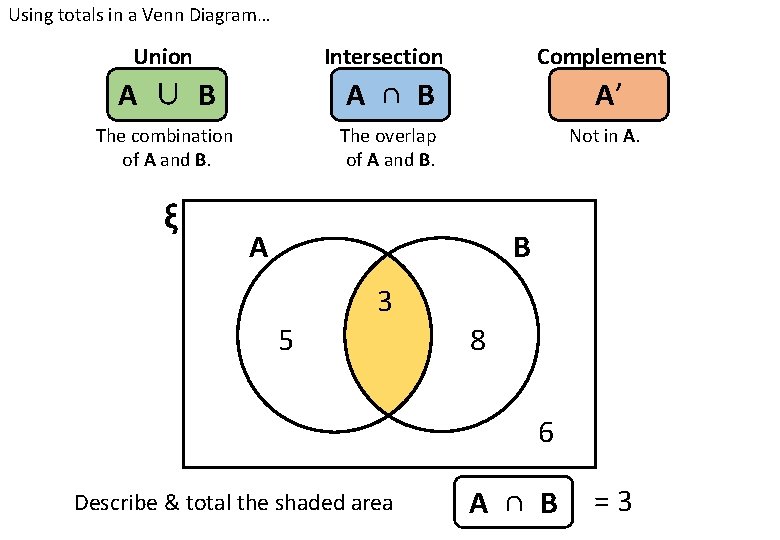
Using totals in a Venn Diagram… Union Intersection Complement A ∪ B A ∩ B A’ The combination of A and B. The overlap of A and B. Not in A. ξ A B 3 5 8 6 Describe & total the shaded area A ∩ B =3

Using totals in a Venn Diagram… Union Intersection Complement A ∪ B A ∩ B A’ The combination of A and B. The overlap of A and B. Not in A. ξ A B 3 5 8 6 Describe & total the shaded area A ∪ B’ = 14

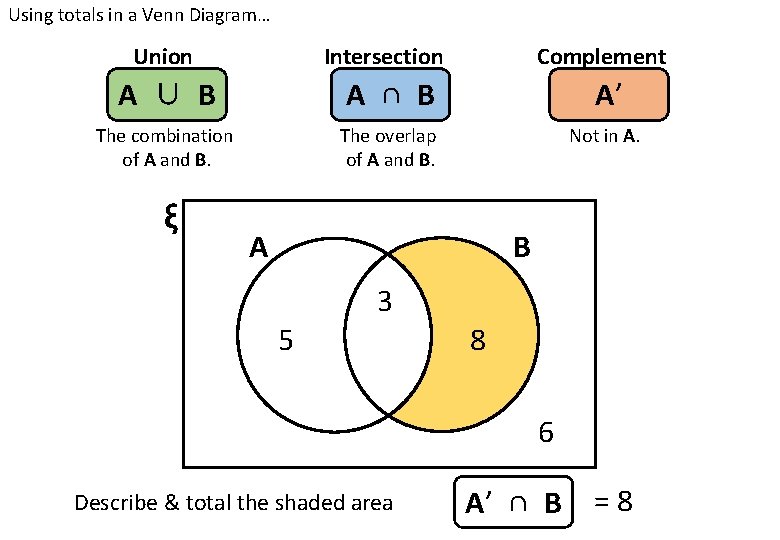
Using totals in a Venn Diagram… Union Intersection Complement A ∪ B A ∩ B A’ The combination of A and B. The overlap of A and B. Not in A. ξ A B 3 5 8 6 Describe & total the shaded area A’ ∩ B =8

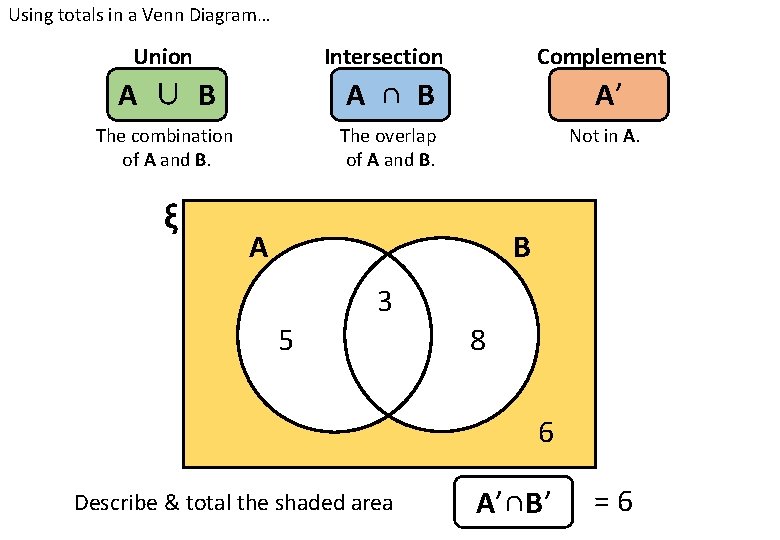
Using totals in a Venn Diagram… Union Intersection Complement A ∪ B A ∩ B A’ The combination of A and B. The overlap of A and B. Not in A. ξ A B 3 5 8 6 Describe & total the shaded area A’∩B’ =6

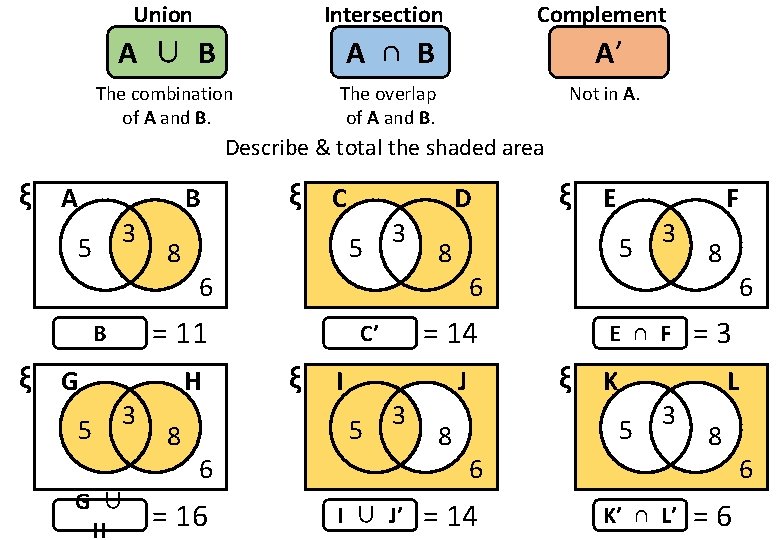
Union Intersection Complement A ∪ B A ∩ B A’ The combination of A and B. The overlap of A and B. Not in A. Describe & total the shaded area ξ A B 3 5 8 ξ G G ∪ H 8 3 6 H 3 D 5 = 11 B 5 ξ C ξ I 5 6 = 16 I ∪ J’ 8 3 6 E ∩ F 8 L 5 3 6 = 14 6 =3 ξ K J 3 F 5 8 = 14 C’ ξ E K’ ∩ L’ 8 =6 6

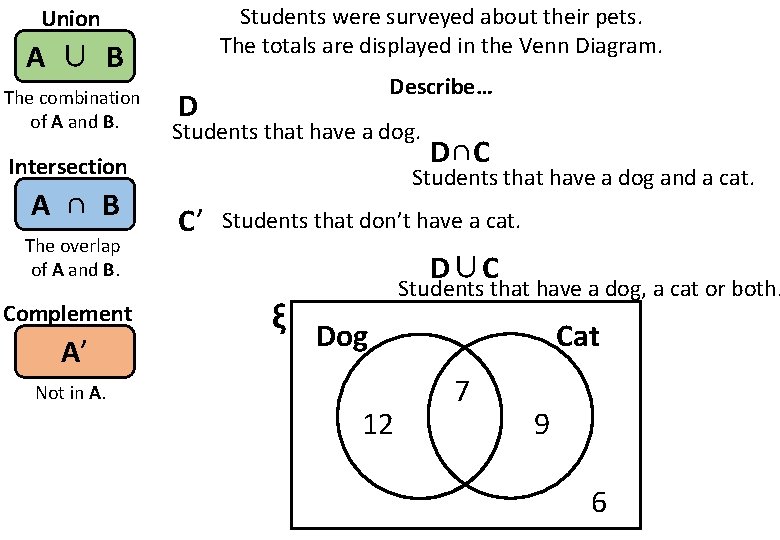
Students were surveyed about their pets. The totals are displayed in the Venn Diagram. Union A ∪ B The combination of A and B. Describe… D Students that have a dog. Intersection A ∩ B The overlap of A and B. Complement A’ Not in A. D∩C Students that have a dog and a cat. C’ Students that don’t have a cat. D∪C ξ Dog 12 Students that have a dog, a cat or both. Cat 7 9 6

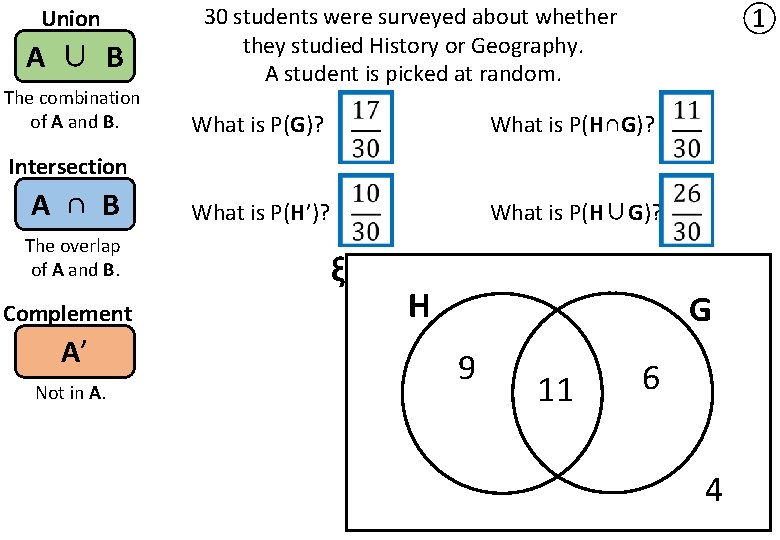
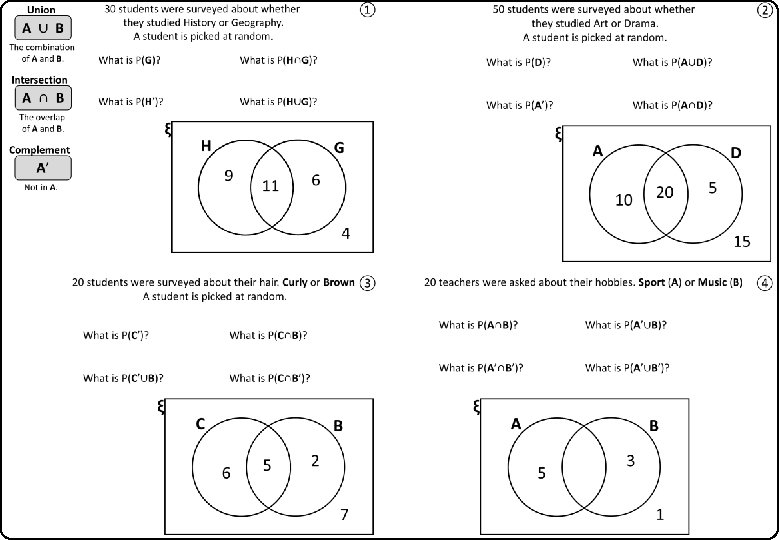
Union A ∪ B The combination of A and B. 30 students were surveyed about whether they studied History or Geography. A student is picked at random. ① What is P(G)? What is P(H∩G)? What is P(H’)? What is P(H∪G)? Intersection A ∩ B The overlap of A and B. Complement A’ Not in A. ξ H G 9 11 6 4

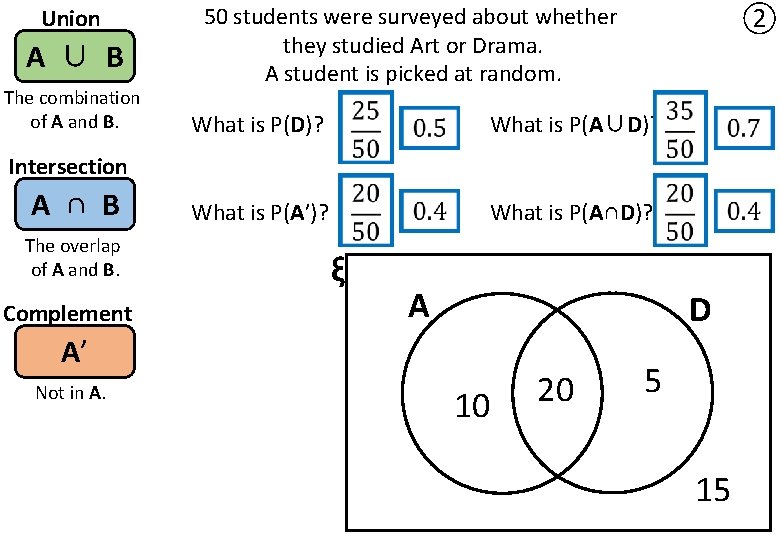
Union A ∪ B The combination of A and B. 50 students were surveyed about whether they studied Art or Drama. A student is picked at random. ② What is P(D)? What is P(A∪D)? What is P(A’)? What is P(A∩D)? Intersection A ∩ B The overlap of A and B. Complement ξ A D A’ Not in A. 10 20 5 15

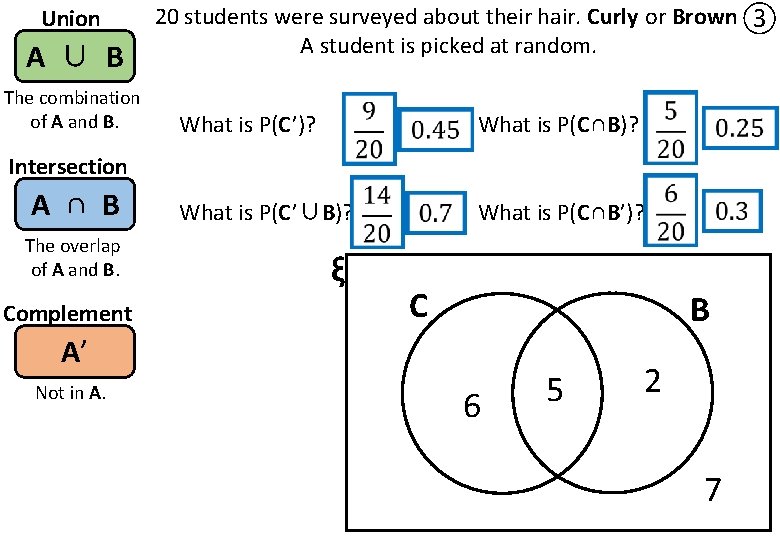
Union A ∪ B The combination of A and B. 20 students were surveyed about their hair. Curly or Brown ③ A student is picked at random. What is P(C’)? What is P(C∩B)? What is P(C’∪B)? What is P(C∩B’)? Intersection A ∩ B The overlap of A and B. Complement ξ C B A’ Not in A. 6 5 2 7

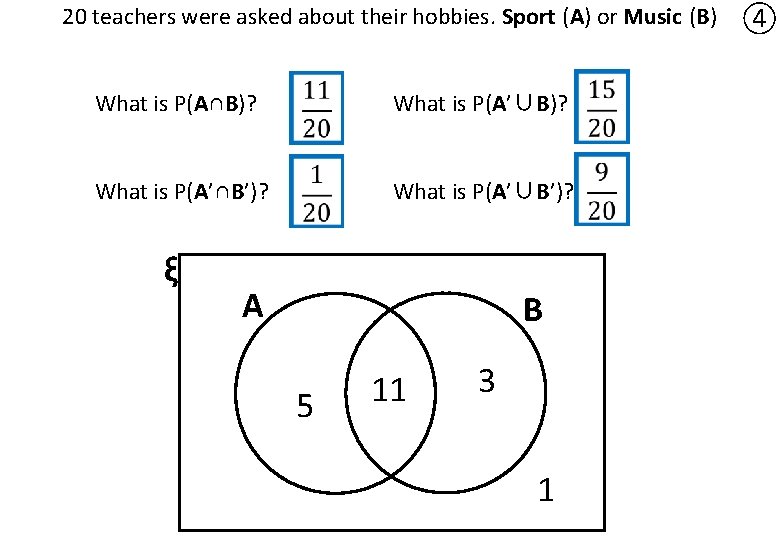
20 teachers were asked about their hobbies. Sport (A) or Music (B) What is P(A∩B)? What is P(A’∪B)? What is P(A’∩B’)? What is P(A’∪B’)? ξ A B 5 11 3 1 ④

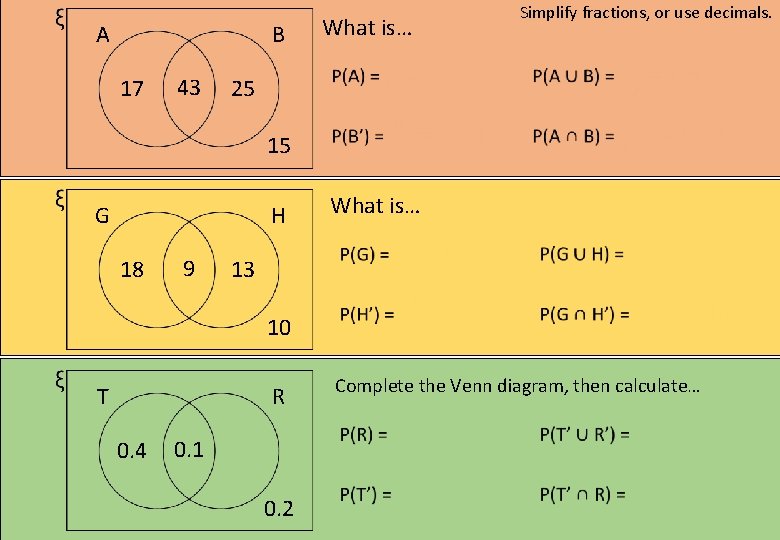
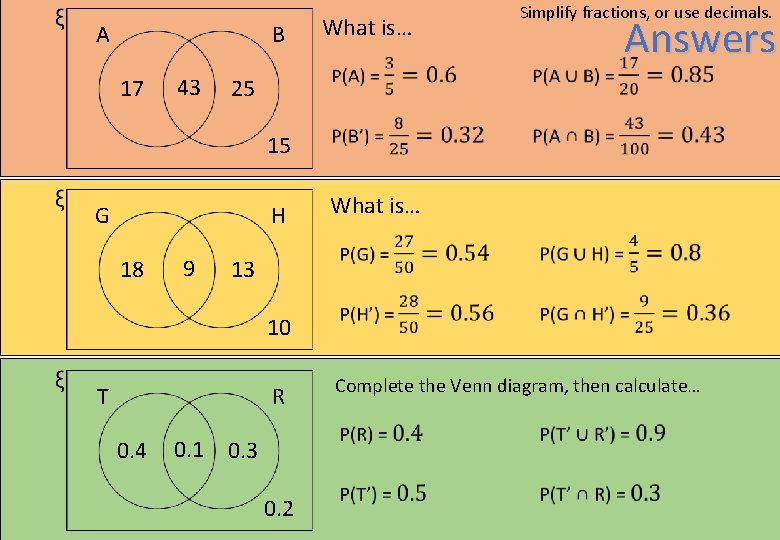
A B 17 43 What is… Simplify fractions, or use decimals. 25 15 G H 18 9 What is… 13 10 T R 0. 4 0. 1 0. 2 Complete the Venn diagram, then calculate…

A B 17 43 What is… Simplify fractions, or use decimals. Answers 25 15 G H 18 9 What is… 13 10 T R 0. 4 0. 1 0. 3 0. 2 Complete the Venn diagram, then calculate…

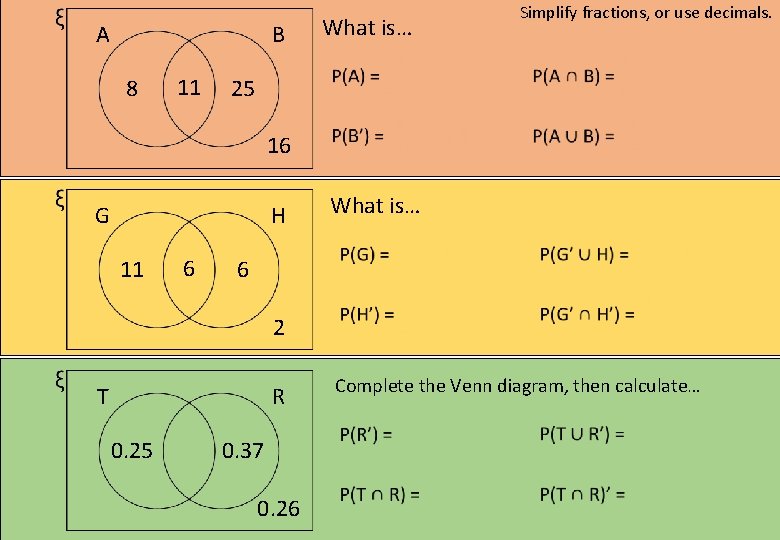
A B 8 11 What is… Simplify fractions, or use decimals. 25 16 G H 11 6 What is… 6 2 T R 0. 25 0. 37 0. 26 Complete the Venn diagram, then calculate…

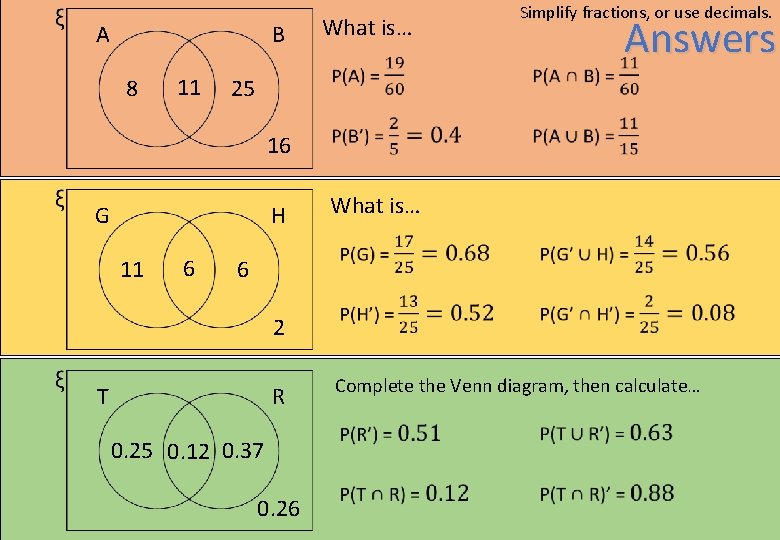
A B 8 11 What is… Simplify fractions, or use decimals. Answers 25 16 G H 11 6 What is… 6 2 T R 0. 25 0. 12 0. 37 0. 26 Complete the Venn diagram, then calculate…

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk