Venn Diagrams In this powerpoint you will learn

Venn Diagrams In this powerpoint, you will learn about Venn diagrams and sets. You will learn about the - universe of your sets unions of sets intersections of sets complements of sets. - Cross products of sets.

Venn Diagrams One way to represent or visualize sets is to use Venn diagrams:

Universe or Universal Set Let U be the set of all students enrolled in classes this semester. U So the universe for any Venn diagram is EVERYTHING, what’s in the circles and everything outside the circles.

U Let M be the set of all students enrolled in Math this semester. Let E be the set of all students enrolled in English this semester. M E

Complement of a set Let C be the set of all students enrolled in classes this semester, but who are not enrolled in Math or English This example shows ~(M U E), or the complement of M union E. It shows all students who took classes, but NOT Math or English. M C U E The complement symbol is either a tilde ( ~ ) or an apostrophe after a letter ( ‘ ), i. e. , ~M ( the complement of M) means we want all students who DID NOT take math. M’ also means the complement of M, so we want ALL students who DID NOT take math.

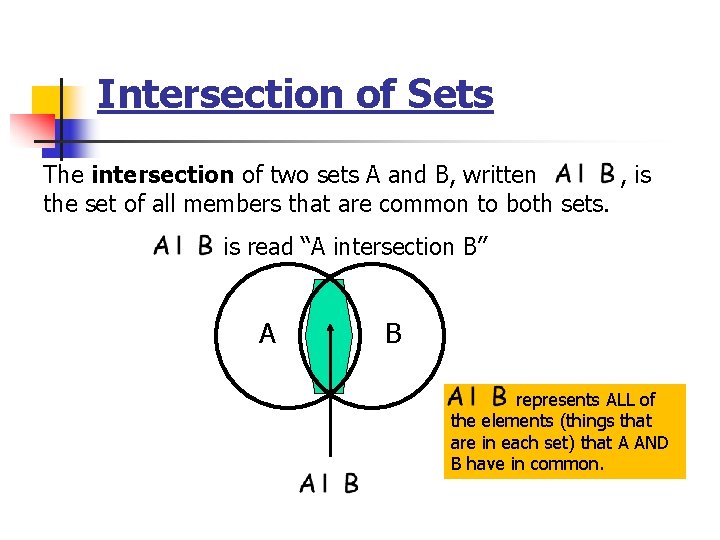
Intersection of Sets The intersection of two sets A and B, written , is the set of all members that are common to both sets. is read “A intersection B” A B represents ALL of the elements (things that are in each set) that A AND B have in common.

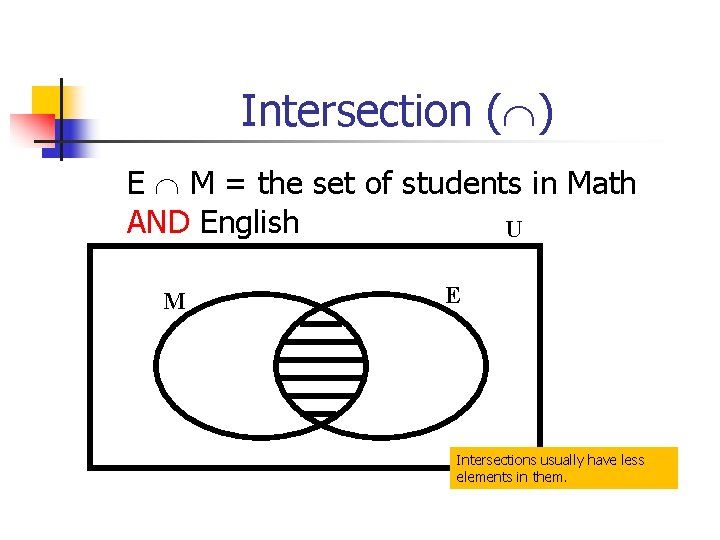
Intersection ( ) E M = the set of students in Math AND English U M E Intersections usually have less elements in them.

Start thinking about complements of sets!! For sets U and V, Ex. #1: ~V = {1, 3} Example Let U = Ex. #2: and V = Find U’ = { 4, 6} . . For intersection, just choose what both sets have in common.

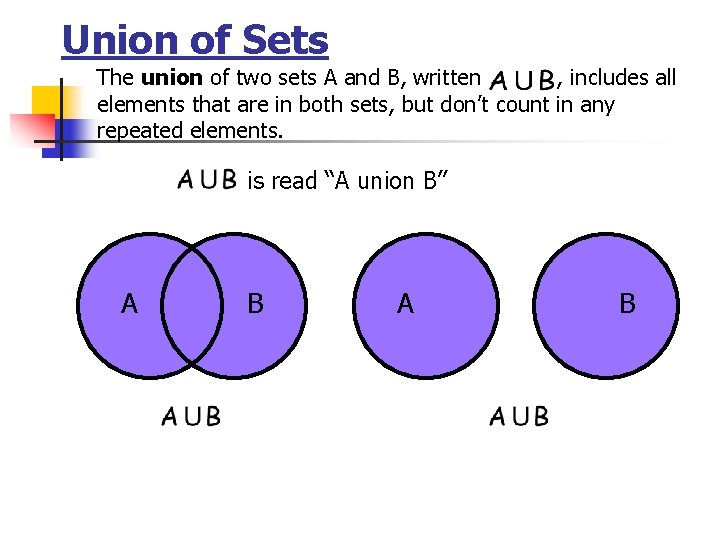
Union of Sets The union of two sets A and B, written , includes all elements that are in both sets, but don’t count in any repeated elements. is read “A union B” A B

TIP!! Unions ( which includes pretty much everything) usually have lots of members, and intersections (what sets have in common) not as many members. Union ( ) E M = the set of students in Math OR English U M E

Example Let C = {0, 1, 2, 3} and D = {1, 3, 5}. Find For union, just choose what both sets have, WITHOUT repeating anything. In this problem, ONLY list the 3 ONCE!

Example Start thinking about complements of sets!! For sets S and T, Ex. #1: S’ = {5, 10} Ex. #2: ~T = { 2, 4} Numbers that are positive AND divide into 4? that would be {1, 2, 4} Let S be the set of positive divisors of 4 and let T = {1, 5, 10}. Find S = {1, 2, 4} We needed a union, so we included all the elements of each set without repeating the 1.

Disjoint Sets Two sets with no elements in common are called disjoint sets. U A set that has no members is often represented by a 0 with a slash through it. Male Students Female Students 0

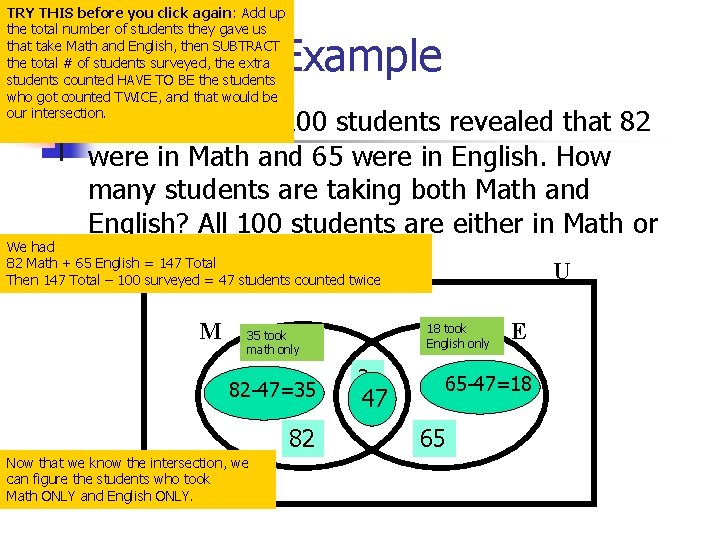
TRY THIS before you click again: Add up the total number of students they gave us that take Math and English, then SUBTRACT the total # of students surveyed, the extra students counted HAVE TO BE the students who got counted TWICE, and that would be our intersection. Example A survey of 100 students revealed that 82 were in Math and 65 were in English. How many students are taking both Math and English? All 100 students are either in Math or We had 82 Math + 65 English = 147 Total U Then 147 Total – 100 surveyed = 47 students counted twice M 18 took English only 35 took math only 82 -47=35 82 Now that we know the intersection, we can figure the students who took Math ONLY and English ONLY. ? 47 E 65 -47=18 65

Try this!! STOP!! 1. 96 Math + 87 English students = 183 Total students Make sure you’ve Since only surveyed, thisintersection, means the # students 2. 120 Nowwere that we know the weofcan 3. Now that we know the intersection, wewho can are counted figure over 120 the intersection, meaning students the are students who took Math ONLY. 96 math answered questions students who tookstudents English ONLY. U 87 taking Math andfigure English. 183 – 120 surveyed = 63 students, thenthe take away the math English students, takeis away the English twice, therefore the 63. of math counted in intersection then intersection and B 4 checkingcounted ALREADY students ALREADY counted in the intersection of english. So, 96 – 63 = 33 math only students. and English. So, 87 – 63 = 24 English only Answers!! M 33 tookmath 24 took E students. English only math only 96 -63=33 96 ? 63 87 -63= 24 87

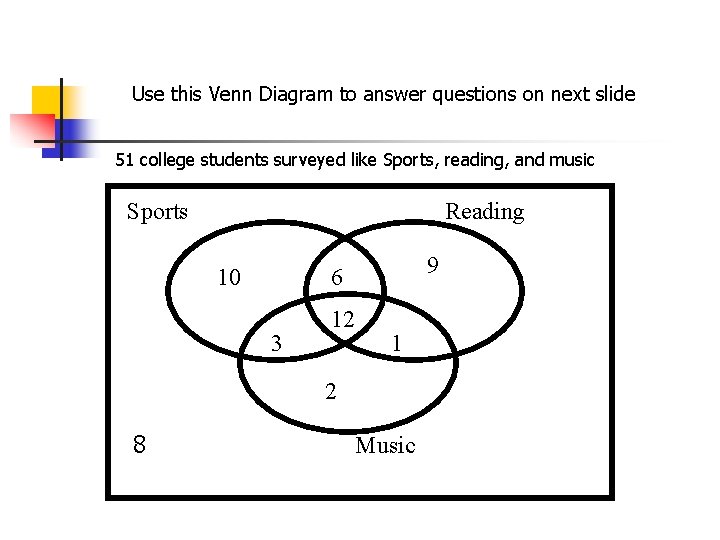
Use this Venn Diagram to answer questions on next slide 51 college students surveyed like Sports, reading, and music Sports Reading 10 9 6 3 12 1 2 8 Music

Venn diagram/Set Questions I n n n A good first step is to identify the elements of each set. On your own paper, name all elements of S= { } R= { } M= { } AND then advance the slide S = { 3, 6, 10, 12} R = { 1, 6, 9, 12} M = { 1, 2, 3, 12}

Venn diagram/Set Questions I Remember, the complement symbol is either a tilde ( ~ ) or an apostrophe after a letter ( ‘ ), i. e. , ~S ( the complement of S) means we want all elements NOT in set S. S’ also means the complement of S, ALL elements NOT in set S. n Find the elements in the following sets using your Venn diagram and the list of sets you just made. Complete as many as possible on your paper BEFORE you advance the slide. You will have to do similar problems on your quiz. 1. S R= 2. ~S = n 3. S U R U M = 4. M’ = n 5. S U R 5. n ~M S

Venn diagram/Set Questions I n n n Find the elements in the following sets using your Venn diagram. A good first step is to identify the elements of each set. Name all elements S = { 3, 6, 10, 12} R = { 1, 6, 9, 12} M = { 1, 2, 3, 12} 1. S R = {6, 12} 2. ~S = {1, 2, 9} S = {3, 6, 10, 12} and R = { 1, 6, 9, 12}, so their intersection contains the set { 6, 12} n 3. S U R U M = We’re looking for all elements NOT in set S, that would be {1, 2, 9} { 1, 2, 3, 6, 9, 10, 12} This would be the union of all sets, so we want everything, but don’t count anything twice. n 5. S U R = { 1, 3, 6, 9, 10, 12} 4. M’ = {6, 9, 10} We’re looking for all elements NOT in set M 5. ~M S = {6, 10} For this problem, list ~M, and list S, and THEN see what the intersection is. ~M={6, 9, 10} S={3, 6, 10, 12} So the intersection of these two sets is {6, 10}

More Challenging Set Questions Solving Strategy n When you work through more challenging set questions, it’s important to work with each part of the problem and build each of those sets first, then work the entire problem. n n Example: (S U R ) M’ We need to make a set for each part of the equation before we make the FINAL set. (S U R ) = = { 1, 3, 6, 9, 10, 12} AND M’ = {6, 9, 10} Now that we’ve built the individual sets, we can look at their intersection. It’s easy to see the intersection. (S U R ) M’ = {6, 9, 10}

Venn diagram Questions II. n Find the elements in the following sets using your Venn diagram. Do on your own paper before you check answers. Our sets are S = { 3, 6, 10, 12} R = { 1, 6, 9, 12} M = { 1, 2, 3, 12} We will add a set T. T = { 1, 5, 7, 8, 9, 10} 1. ~M U (S T) 2. (R U S)’ M n 3. R’ (SUT) 4. ~T U ~( R U S) n 5. ( R T) 6. S U ( R U T)’ n n ( S U T)’

Venn diagram Questions II. n n Find the elements in the following sets using your Venn diagram. Our sets are S = { 3, 6, 10, 12} R = { 1, 6, 9, 12} M = { 1, 2, 3, 12} We will add a set T. T = { 1, 5, 7, 8, 9, 12} 1. ~M U (S T)= {5, 6, 7, 8, 9, 10} 2. (R U S )’ U M= {1, 2, 3, 5, 7, 8, 12} ~M = {5, 6, 7, 8, 9, 10} and S intersect T = {10}, so their union contains the set { 5, 6, 7, 8, 9, 10} n 3. R’ ( S U T ) = {3, 5, 7, 8, 10} R’ = {2, 3, 5, 7, 8, 10} and S U T= {1, 3, 5, 6, 7, 8, 9, 10, 12}, so their intersection contains the set { 3, 5, 7, 8, 10} n 5. ( R T) ( S U T)’ = 0 R intersect T = {1, 9, 12} and (S U T)’= {2}, so their intersection contains nothing , the empty set notation, which is a 0 with a line through it. (R U S )’ = {2, 5, 7, 8} M={ 1, 2, 3, 12} The union of these 2 sets would be { 1, 2, 3, 5, 7, 8, 12} 4. ~T U ~( R U S)= {2, 3, 5, 6, 7, 8, 10} ~T = {2, 3, 6, 10} and ~(R U S) = {2, 5, 7, 8}, so their union contains the set { 2, 3, 5, 6, 7, 8, 10} 6. S U ( R U T)’ = {2, 3, 6, 10, 12} S = {3, 6, 10, 12} and (R U T)’ = {2, 3, 10}, so their union contains the set { 2, 3, 6, 10, 12}

Venn diagram Questions III. n n n n Use your Venn diagram to answer the following questions. 1. How many students like more than 1 activity? 2. How many students did not participate in any of these activities? 3. How many students liked exactly one activity? 4. How many students like more then 2 activities? 5. How many students like 1 or more activities? 6. How many students liked exactly 2 activities? 7. How many students liked ONLY reading?

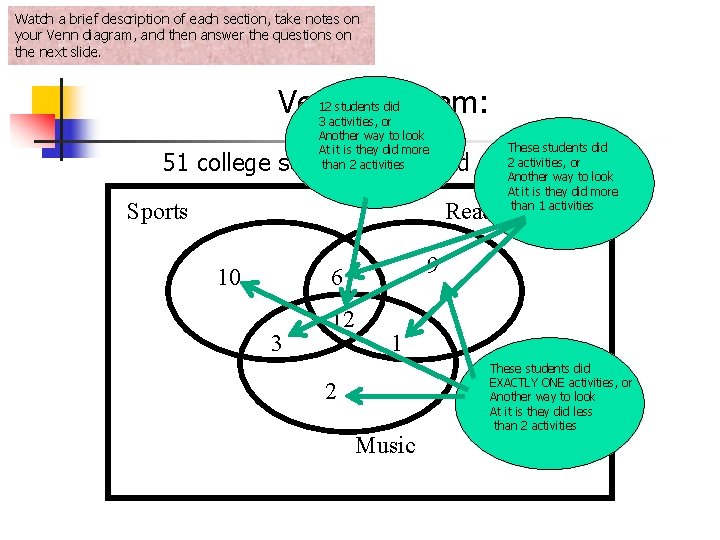
Watch a brief description of each section, take notes on your Venn diagram, and then answer the questions on the next slide. Venn Diagram: 12 students did 3 activities, or Another way to look At it is they did more than 2 activities 51 college students surveyed Sports These students did 2 activities, or Another way to look At it is they did more than 1 activities Reading 10 9 6 3 12 1 2 Music These students did EXACTLY ONE activities, or Another way to look At it is they did less than 2 activities

Venn diagram Questions III. Use your Venn diagram to answer the following questions. n 1. How many students like more than 1 activity? n n 2. How many students did not participate in any of these activities? n n n 1 or more means 1, 2, or 3, so this would be everyone in the Venn diagram, or 43 students 6. How many students liked exactly 2 activities? n n More than 2 means 3 or more, which is JUST the middle or 12 students. 5. How many students like 1 or more activities? n n This would be just the very outside 10+9+2 = 21 students 4. How many students like more than 2 activities? n n Add up the numbers of students in your Venn diagram that like these activities. (43) Take your total surveyed ( 51) – 43 = 8 students who did not like sports, reading, or music. 3. How many students liked exactly one activity? n n More than 1 means 2 or more, so 1+3+6+12 = 22 students. 1+6+3 = 10 students 7. How many students liked ONLY reading? n ONLY reading means they read, but weren’t in the Music or Sports, this would be 9 students.

Cross Products of Sets You get the cross product of a set ( or cartesian product) when you multiply two sets together ( Set A x Set B)resulting in a new set, where each member of set 1 is now paired with a member of set 2. Sounds complicated, but it’s really easy!! Look at this example. n For example, let A = {1, 2} and B = {x, y, z} Then A×B = {1, 2} x {x, y, z} = {(1, x), (1, y), (1, z), (2, x), (2, y), (2, z)}. Wasn’t that easy, try one on next slide!

Try these cross products on your own paper. Let A = {1, 2}; B = {3, 4} 1. A × B = {1, 2} × {3, 4} = {( , ), ( , )} {(1, 3), (1, 4), (2, 3), (2, 4)} 2. B ×A = {3, 4} × {x, z} = {( , ), ( , )} {(3, x), (3, z), (4, x), (4, z)} Quiz directions are on slide AFTER practice slides.

Practice Websites Sets Practice Questions Venn Diagram Practice Quiz

That quiz Instructions n n n Go to www. portal. com , mrjalg Choose That Quiz section Choose your class Choose your name Your PW is your initials in CAPS followed by the number associated with your first name initial n Examples: n n Adam Jordan = AJ 1 Spencer Johnson = SJ 19 Zelda Sparkles = ZS 26 Belinda Bonkers = BB 2