Venkatesan Guruswami CMU Yury Makarychev TTIC Prasad Raghavendra

Venkatesan Guruswami (CMU) Yury Makarychev (TTI-C) Prasad Raghavendra (Georgia Tech) David Steurer (MSR) Yuan Zhou (CMU)

Bipartite graph recognition • Depth-first search/breadth-first search • With some noise? – Given a bipartite graph with 1% noisy edges, can we remove a small fraction of edges (10% say) to get a bipartite graph, i. e. can we divide the vertices into two parts, so that 90% of the edges go accross the two parts?

Max. Cut • cut(A, B) = edges(A, B) / |E| where B = V - A • exact one of i, j in A : edge (i, j) "on the cut" • Max. Cut: find A, B such that cut(A, B) is maximized G=(V, E) A B=V-A cut(A, B) = 4/5 subject to – Bipartite graph recognition: Max. Cut = 1 ? – Robust bipartite graph recognition: given Max. Cut ≥ 0. 99, to find cut(A, B) ≥ 0. 9

c vs. s approximation for Max. Cut • Given a graph with Max. Cut value at least c, can we find a cut of value at least s ? • Robust bipartite graph recognition: given Max. Cut ≥ 0. 99, to find cut(A, B) ≥ 0. 9 – 0. 99 vs 0. 9 approximation – "approximating almost perfect Max. Cut"

Robust bipartite graph recognition • Task: given Max. Cut ≥ 0. 99, find cut(A, B) ≥ 0. 9 • We can always find cut(A, B) ≥ 1/2. – Assign each vertex -1, 1 randomly – For any edge (i, j), E[(1 - xixj)/2] = 1/2 vi vj

Robust bipartite graph recognition (cont'd) • Task: given Max. Cut ≥ 0. 99, find cut(A, B) ≥ 0. 9 • We can always find cut(A, B) ≥ 1/2. • Better than 1/2? – DFS/BFS/greedy? No combinatorial algorithm known until very recent [KS 11] – Linear Programming? Natural LPs have big Integrality Gaps [VK 07, STT 07, CMM 09]

Robust bipartite graph recognition (cont'd) • Task: given Max. Cut ≥ 0. 99, find cut(A, B) ≥ 0. 9 • We can always find cut(A, B) ≥ 1/2. • Better than 1/2? • The GW Semidefinite Programming relaxation [GW 95] subject to – 0. 878 -approximation – Given Max. Cut , can find a cut • vs approximation, tight under Unique Games Conjecture [Kho 02, KKMO 07, MOO 10]

Robust satisfiability algorithms • Given an instance which can be satisfied by removing ε fraction of constraints, to make the instance satisfiable by removing g(ε) fraction of constraints – g(ε) -> 0 as ε -> 0 • Examples • vs. [Zwick 98] algorithm for Max. Cut [GW 95] algorithm for Max 2 SAT [Zwick 98] algorithm for Max. Horn 3 SAT

Max. Bisection G = (V, E) A Objective: B subject to

Max. Bisection (cont'd) G = (V, E) A Objective: B • Approximating Max. Bisection? – No easier than Max. Cut • Reduction: take two copies of the Max. Cut instance

Max. Bisection (cont'd) G = (V, E) A Objective: B • Approximating Max. Bisection? – No easier than Max. Cut – Strictly harder than Max. Cut? – Approximation ratio: 0. 6514 [FJ 97], 0. 699 [Ye 01], 0. 7016 [HZ 02], 0. 7027 [FL 06] – Approximating almost perfect solutions? Not known

Finding almost-perfect Max. Bisection • Question – Is there a vs for Max. Bisection, where approximation algorithm ? • Answer. Yes. • Our result. – Theorem. There is a vs approximation algorithm for Max. Bisection. – Theorem. Given a satisfiable Max. Bisection instance, it is easy to find a (. 49, . 51)-balanced cut of value.

Extension to Min. Bisection • Min. Bisection – minimize edges(A, B)/|V|, s. t. B = V - A, |B| = |A| • Our result – Theorem. There is a vs approximation algorithm for Max. Bisection. – Theorem. Given a Min. Bisection instance of value , it is easy to find a (. 49, . 51)-balanced cut of value.

The rest of this talk. . . • Previous algorithms for Max. Bisection. • Theorem. There is a vs approximation algorithm for Max. Bisection.

Previous algorithms for Max. Bisection

The GW algorithm for (almost perfect) Max. Cut [GW 95] • Max. Cut objective subject to Max. Cut = 2/3 -1 • SDP relaxation 0 1 subject to SDP ≥ Max. Cut In this example: SDP = 3/4 > Max. Cut

The "rounding" algorithm subject to • Lemma. We can (in poly time) get a cut of value when • Algorithm. Choose a random hyperplane, the hyperplane divides the vertices into two parts. • Analysis.

The "rounding" algorithm (cont'd) subject to • Lemma. We can (in poly time) get a cut of value when • Algorithm. Choose a random hyperplane, the hyperplane divides the vertices into two parts. • Analysis. – implies for most edges (i, j), their SDP contribution is large – Claim. If , then – Therefore, the random hyperplane cuts many edges (in expectation)

The "rounding" algorithm (cont'd) – Claim. If – Proof. vi , then vi, vj seperated by the hyperplane vj vi, vj not seperated by the hyperplane

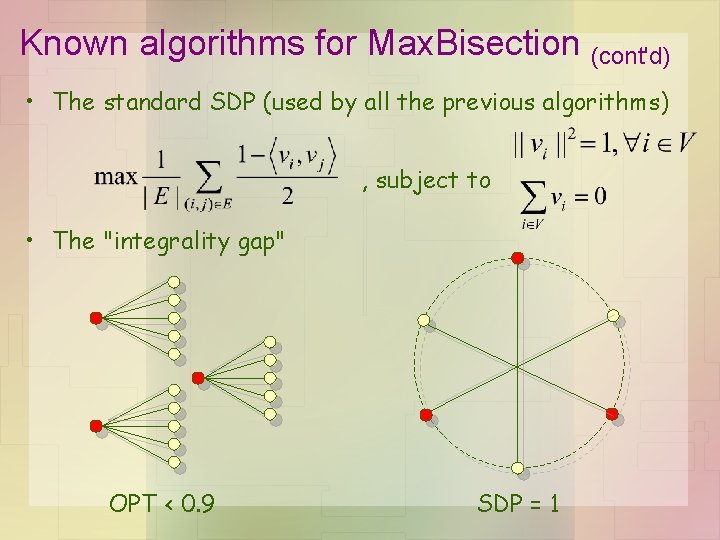
Known algorithms for Max. Bisection • The standard SDP (used by all the previous algorithms) , subject to Bisection condition • Gives non-trivial approximation gaurantee • But does not help find almost perfect Max. Bisection

Known algorithms for Max. Bisection (cont'd) • The standard SDP (used by all the previous algorithms) , subject to • The "integrality gap" OPT < 0. 9 SDP = 1

Known algorithms for Max. Bisection (cont'd) • The standard SDP (used by all the previous algorithms) , subject to • The "integrality gap" : instances that OPT < 0. 9, SDP = 1 • Why is this a bad news for SDP? – Instances that OPT > 1 - ε, SDP > 1 - ε – Instances that OPT < 0. 9, SDP > 1 - ε – SDP cannot tell whether an instance is almost satisfiable (OPT > 1 - ε) or not.

Our approach

• Theorem. There is a vs approximation algorithm for Max. Bisection.

A simple fact • Fact. of value . -balanced cut of value bisection • Proof. Get the bisection by moving fraction of random vertices from the large side to the small side. – fraction of cut edges affected : at most in expectation • Only need to find almost bisections.

Almost perfect Max. Cuts on expanders • λ-expander: for each we have , such that , where G=(V, E) S ,

Almost perfect Max. Cuts on expanders (cont'd) • λ-expander: for each we have , such that , where , • Key Observation. The (volume of) difference between two cuts on a λ-expander is at most. • Proof. C X A B Y D

Almost perfect Max. Cuts on expanders (cont'd) • λ-expander: for each we have , such that , where , • Key Observation. The (volume of) difference between two cuts on a λ-expander is at most. • Approximating almost perfect Max. Bisection on expanders is easy. – Just run the GW alg. to find the Max. Cut.

The algorithm (sketch) • Decompose the graph into expanders – Discard all the inter-expander edges • Approximate OPT's behavior on each expander by finding Max. Cut (GW) – Discard all the uncut edges • Combine the cuts on the expanders – Take one side from each cut to get an almost bisection. (subset sum) 2: 1: Step 3: find decompose Max. Cut into combine pieces G=(V, E) expanders

Expander decomposition • Cheeger's inequality. Can (efficiently) find a cut of sparsity if the graph is not a -expander. • Corollary. A graph can be (efficiently) decomposed into -expanders by removing edges (in fraction). • Proof. – If the graph is not an expander, divide it into small parts by sparsest cut (cheeger's inequality). – Process the small parts recursively. G=(V, E) λ-expander

The algorithm • Decompose the graph into – Lose edges. -expanders. • Apply GW algorithm on each expander to approximate OPT. – OPT(Max. Bisection) = – GW finds cuts on these expanders • different from behavior of OPT – Lose edges. • Combine the cuts on the expanders (subset sum). • • -balanced cut of value a bisection of value

• Proved: • Theorem. There is a vs approximation algorithm for Max. Bisection. • Will prove: • Theorem. There is a vs approximation algorithm for Max. Bisection. short story

Eliminating the factor • Recall. Only need to find almost bisections ( a bisection) -close to • Observation. Subset sum is "flexible with small items" – Making small items (101, 304) more biased does not (397, 201) change the solution (8, (3, 0) 5) too much. (8, (6, 0) 2) sum (6, (5, 0) 1) (5, (3, 0) 2) (515, 515)

Eliminating the factor • Recall. Only need to find almost bisections ( a bisection) -close to • Observation. Subset sum is "flexible with small items" – Making small items (101, 304) more biased does not (397, 201) change the solution (8, 0) too much. (8, 0) sum (6, 0) (5, 0) (498, 505)

Eliminating the factor • Recall. Only need to find almost bisections ( a bisection) -close to • Observation. Subset sum is "flexible with small items" – Making small items (101, 304) more biased does not (397, 201) change the solution (8, 0) too much. (8, 0) sum (6, 0) (506, 505)

Eliminating the factor • Recall. Only need to find almost bisections ( a bisection) -close to • Observation. Subset sum is "flexible with small items" – Making small items (101, 304) more biased does not (397, 201) change the solution (8, 0) too much. (0, 8) sum (6, 0) (506, 513)

Eliminating the factor • Recall. Only need to find almost bisections ( a bisection) -close to • Observation. Subset sum is "flexible with small items" – Making small items (101, 304) more biased does not (397, 201) change the solution (8, 0) too much. (0, 8) sum (6, 0) (512, 513)

Eliminating the factor • Recall. Only need to find almost bisections ( a bisection) -close to • Observation. Subset sum is "flexible with small items" – Making small items (101, 304) more biased does not (397, 201) change the solution (8, 0) too much. (0, 8) sum (6, 0) (517, 513)

Eliminating the factor • Recall. Only need to find almost bisections ( a bisection) -close to • Observation. Subset sum is "flexible with small items" – Making small items (200, 0) more biased does not (0, 2) change the solution (0, 2) too much. 100 – However, making small items copies more balanced might be a bad idea. (0, 2) sum (200, 200)

Eliminating the factor • Recall. Only need to find almost bisections ( a bisection) -close to • Observation. Subset sum is "flexible with small items" – Making small items (200, 0) more biased does not (1, 1) change the solution (1, 1) too much. 100 – However, making small items copies more balanced might be a bad idea. (1, 1) sum (300, 100)

Eliminating the factor (cont'd) • Idea. Terminate early in the decomposition process. Decompose the graph into – -expanders (large items), or – subgraphs of vertices (small items). • Corollary. Only need to discard edges. • Lemma. We can find an almost bisection if the Max. Cuts we get for small sets are more biased than those in OPT.

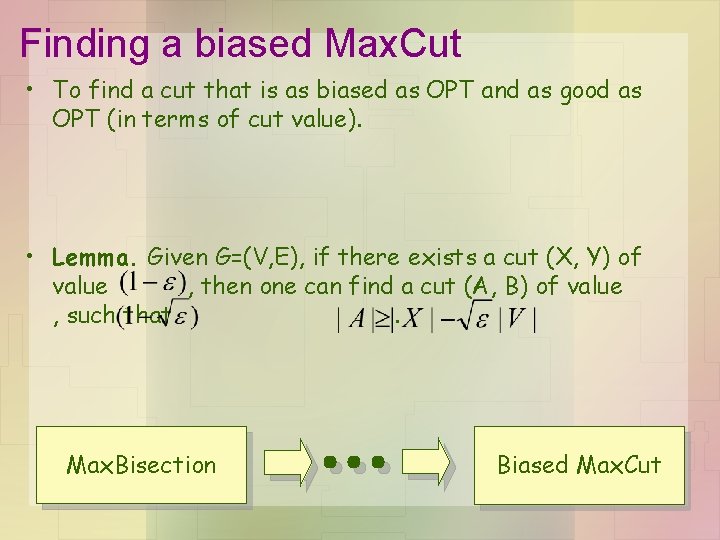
Finding a biased Max. Cut • To find a cut that is as biased as OPT and as good as OPT (in terms of cut value). • Lemma. Given G=(V, E), if there exists a cut (X, Y) of value , then one can find a cut (A, B) of value , such that. Max. Bisection Biased Max. Cut

The algorithm • Decompose the graph into – Lose edges. -expanders or small parts. • Apply GW algorithm on each expander to approximate OPT. – Lose edges, different from OPT • Find biased Max. Cuts in small parts. – Lose edges, at most less biased than OPT • Combine the cuts on the expanders and small parts (subset sum). • • -balanced cut of value a bisection of value

Finding a biased Max. Cut -- A simpler task • Lemma. Given G=(V, E), if there exists a cut (X, Y) of value , then one can find a cut (A, B) of value , such that. • SDP. maximize --- Bias subject to --- Cut value • Claim. SDP ≥ |X|/|V|

Rounding algorithm (sketch) • Goal: given SDP solution, to find a cut (A, B) such that – – • For most ( fraction) edges (i, j), we have • vi, vj are almost opposite to each other: vi ≈ - vj, • Indeed,

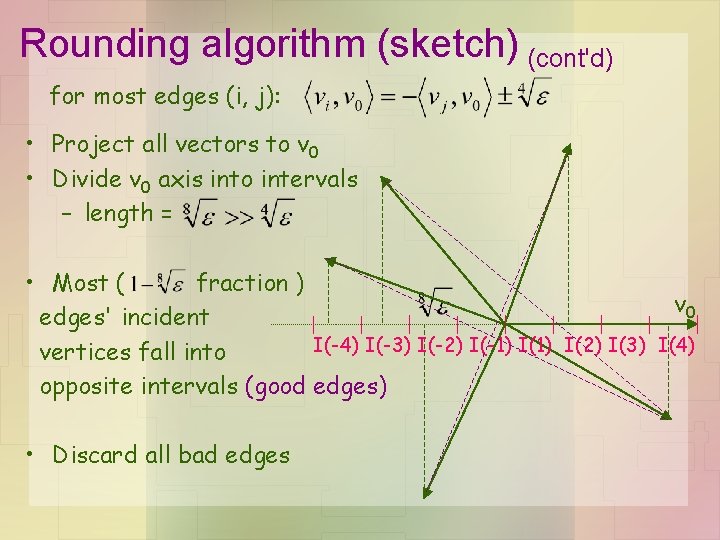
Rounding algorithm (sketch) (cont'd) for most edges (i, j): • Project all vectors to v 0 • Divide v 0 axis into intervals – length = • Most ( fraction ) v 0 edges' incident I(-4) I(-3) I(-2) I(-1) I(2) I(3) I(4) vertices fall into opposite intervals (good edges) • Discard all bad edges

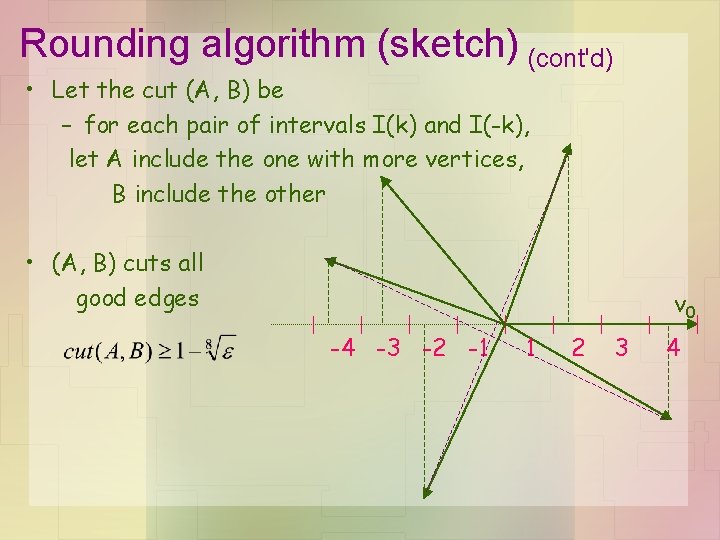
Rounding algorithm (sketch) (cont'd) • Let the cut (A, B) be – for each pair of intervals I(k) and I(-k), let A include the one with more vertices, B include the other • (A, B) cuts all good edges v 0 -4 -3 -2 -1 1 2 3 4

Rounding algorithm (sketch) (cont'd) • Let the cut (A, B) be – for each pair of intervals I(k) and I(-k), let A include the one with more vertices, B include the other • For each i in I(k) For each i in I(-k)

Finding a biased Max. Cut • Lemma. Given G=(V, E), if there exists a cut (X, Y) of value , then one can find a cut (A, B) of value , such that. • SDP. maximize --- Bias subject to --- Cut value -triangle inequality

Future directions • vs approximation? • "Global conditions" for other CSPs. – Balanced Unique Games?

The End. Any questions?

Eliminating the factor • Another key step. • Idea. Terminate early in the decomposition process. Decompose the graph into -expanders or subgraphs of vertices. • Corollary. Only need to discard edges. • Lemma. We can find an almost bisection if the Max. Cuts for small sets are more biased than those in OPT. Max. Bisection Biased Max. Cut

Finding a biased Max. Cut • Lemma. Given G=(V, E), if there exists a cut (X, Y) of value , then one can find a cut (A, B) of value , such that. • SDP. maximize subject to -triangle inequality • Rounding. A hybrid of hyperplane and threshold rounding.

Future directions • vs approximation? • "Global conditions" for other CSPs. – Balanced Unique Games?

The End. Any questions?