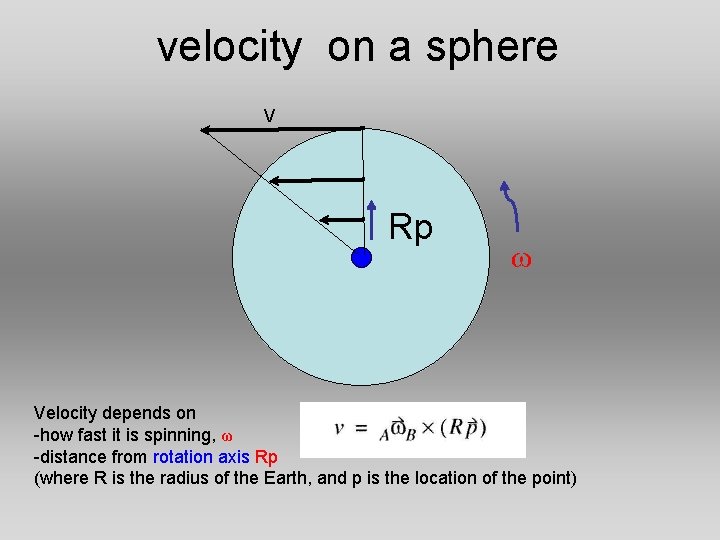
velocity on a sphere V Rp Velocity depends









- Slides: 12

velocity on a sphere V Rp ω Velocity depends on -how fast it is spinning, ω -distance from rotation axis Rp (where R is the radius of the Earth, and p is the location of the point)

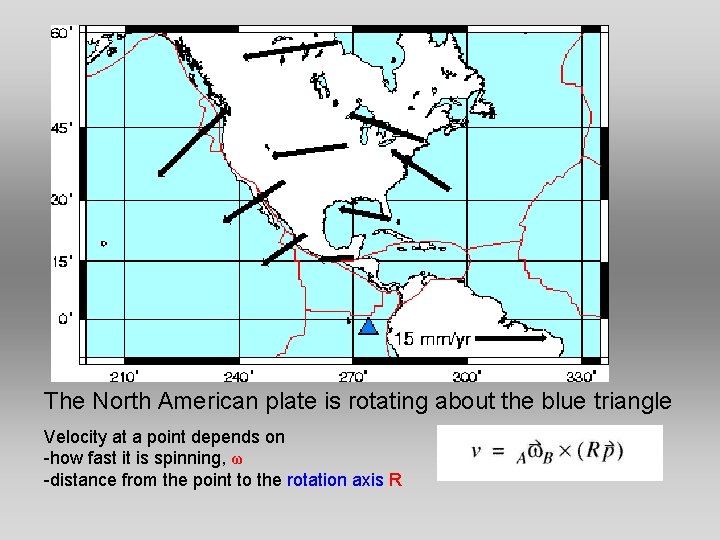
The North American plate is rotating about the blue triangle Velocity at a point depends on -how fast it is spinning, ω -distance from the point to the rotation axis R

We’ll be finding relative velocities of a point on one plate with respect to another plate Ex: What is the velocity of Mauritania relative to the NA plate? Mauritania

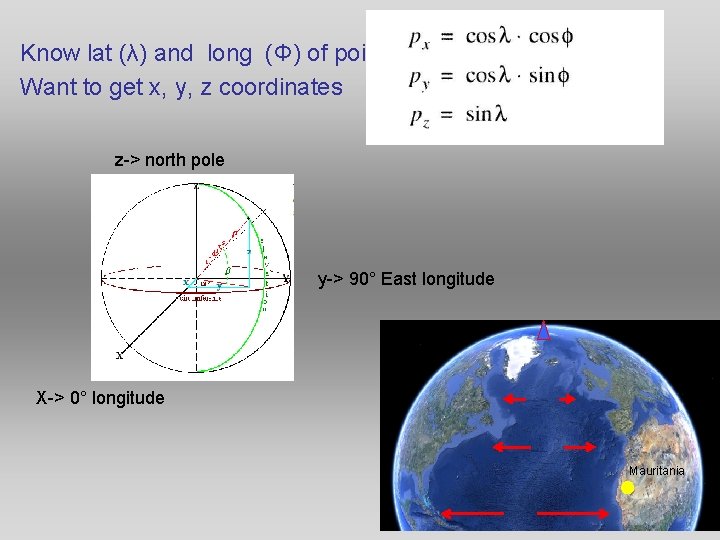
What is the velocity of Mauritania relative to the NA plate? Table 1 gives us the plate rotation vectors (the angular velocity and the lat long of the Euler pole) We want velocities in terms of N-S, E-W, up-down: Ex: Avpb=0. 5 cm/yr north + 2. 0 cm/yr east need to do some conversions: Know lat (λ) and long (Φ) of point Want to get x, y, z coord. Mauritania

Know lat (λ) and long (Φ) of point Want to get x, y, z coordinates z-> north pole y-> 90° East longitude X-> 0° longitude Mauritania

Now we have the coordinates of p Can get velocity Which gives us velocity in x, y, z space But, want local geographic coord. Mauritania

But, want local geographic coord. (N-S, E-W, up-down) Mauritania

Now have velocity in terms of North, East, and up-down Ex: Avpb=0. 5 cm/yr north + 2. 0 cm/yr east Can also determine magnitude and direction of relative velocity Ex. 45 mm/yr 102° SE Mauritania

Today’s lab • Functions vs scripts • Today you’ll be making functions- a function is slightly fancier than a script. • A function can be run from the command line, with input and output variables • Today you will be writing a function to compute the relative velocity of a point on one plate with respect to another plate

Today’s lab • plate_vel. m will be a function • The first line of your code will declare that plate_vel is a function • Function vl=plate_vel(lat, lon, latp, lonp, omega) – v 1 will be the output (the velocity of the point) – (lat, lon, latp, lonp, omega) will be the input (the location of the point, location of the euler pole, and the rotational velocity • So, once you have written and saved the function, you can go to the command line and get the velocity of a point relative to another plate

Today’s lab • To find the velocity of a point on the Pacific plate (at lat=37° and long=-123°) relative to North America by look up the rotation vector in table 1 (48. 7, -78. 2, 0. 78) and type • Vl=plate_vel(37, -123, 48. 7, -78. 2, 0. 78) – Matlab will return Which are the N-S E-W up-down Components of the velocity

Note error in table: • Nazca-Pacific… longitude of Euler pole is 90. 1 E