Vektor kalkulus Deloperator Definisjon og anvendelse Deloperator Gradient

Vektor kalkulus

Del-operator Definisjon og anvendelse Del-operator Gradient Divergens Curl Retningsderivert Fluks Sirkulasjon / Rotasjon

Curl Sammenheng mellom curl og rotasjon Posisjon Hastighet

Konservativt vektorfelt Vei-uavhengighet F definert i et åpent område D i rommet. La være uavhengig av alle veier mellom A og B for alle A, B D. B A Vi sier da at integralet er vei-uavhengig. Vi sier videre at F er konservativ og at vektorfeltet er konservativt.

Potensial-funksjon F definert i et åpent område D i rommet. Hvis det finnes en skalar-funksjon f som er slik at F= f så kalles f for en potensial-funksjon til F og vektorfeltet kalles for et gradientfelt. F er gradienten til f

Gradientfelt og vei-uavhengighet F definert i et åpent område D i rommet. Bevis del 1: Anta at det finnes en f slik at F = f. Det finnes en f slik at F = f vei-uavhengig dvs, integralet er vei-uavhengig, kun avhengig av endepunktene.

Vei-uavhengighet og null-integral for lukkede kurver F definert i et åpent område D i rommet. F er konservativ på D (dvs vei-uavhengig) C 2 B A C 1 Bevis:

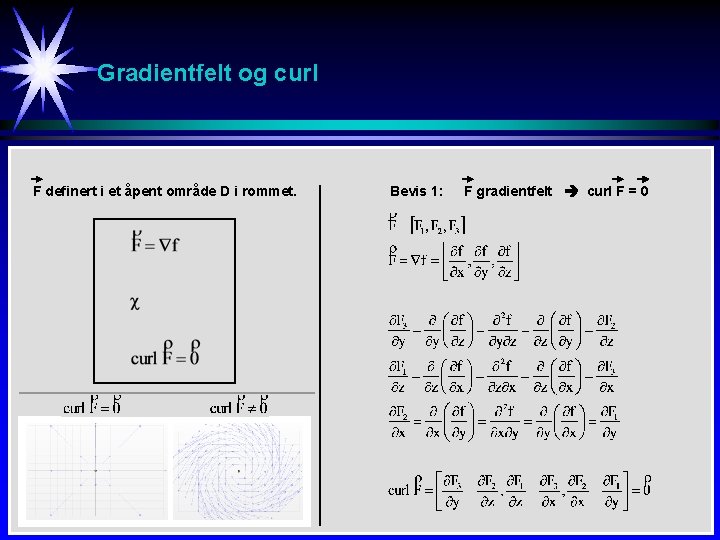
Gradientfelt og curl F definert i et åpent område D i rommet. Bevis 1: F gradientfelt curl F = 0

Gradientfelt og eksakt differentialform F = [ F 1, F 2, F 3] definert i et åpent område D i rommet. Uttrykket F 1 dx + F 2 dy + F 3 dz er en differential form. Differentialformen kalles eksakt hvis det finnes en skalar funksjon f slik at

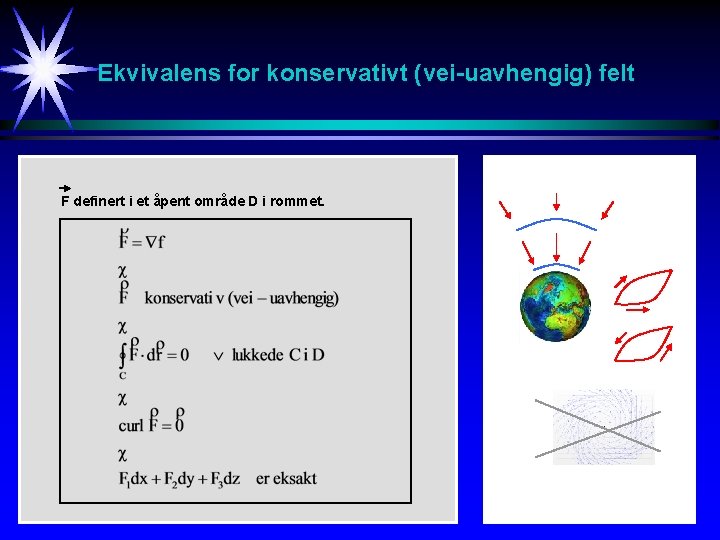
Ekvivalens for konservativt (vei-uavhengig) felt F definert i et åpent område D i rommet.

Konservativt vektorfelt Eks 1 - Oppgave F = [ excosy + yz, xz – exsiny, xy + z ] 1. Vis at F er konservativ (vei-uavhengig) 2. Bestem en potensialfunksjon til F 3. Bestem vei-integralet til F langs den rette linjen fra A = (1, 2, 3) til B = (7, 9, -1)

Konservativt vektorfelt Eks 1 - Løsning [1/3] F = [ excosy + yz, xz – exsiny, xy + z ] 1. Tilstrekkelig å vise at curl F = 0

Konservativt vektorfelt Eks 1 - Løsning [2/3] F = [ excosy + yz, xz – exsiny, xy + z ] 2. Bestem en potensialfunksjon til F

Konservativt vektorfelt Eks 1 - Løsning [3/3] F = [ excosy + yz, xz – exsiny, xy + z ] 3. Bestem vei-integralet av F langs den rette linjen fra A = (1, 2, 3) til B = (7, 9, -1)

Konservativt vektorfelt Eks 2 - Oppgave 1. Vis at ydx + xdy + 4 z er eksakt 2. Bestem følgende integral langs den rette linjen mellom de gitte punktene: A (1, 1, 1) B (2, 3, -1)

Konservativt vektorfelt Eks 2 - Løsning [1/4] 1. Tilstrekkelig å vise at curl F = 0 Herav: ydx + xdy + 4 dz er eksakt

Konservativt vektorfelt Eks 2 - Løsning [2/4] 2. Bestemmelse av potensialfunksjon f

Konservativt vektorfelt Eks 2 - Løsning [3/4] F = [ y, x, 4] 2. Bestem vei-integralet av F langs den rette linjen fra A = (1, 1, 1) til B = (2, 3, -1) A (1, 1, 1) F B (2, 3, -1)

Konservativt vektorfelt Eks 2 - Løsning [4/4] 2. Integralet kan også løses direkte A (1, 1, 1) A F B (2, 3, -1) B

Divergens Curl (Flukstetthet) (Sirkulasjonstetthet) Fluks k C Strømning T n F Divergens d. A d. C C k A T n F Curl

Divergens (Flukstetthet) Def - 2 D [1/3]

Divergens (Flukstetthet) Def - 2 D [2/3]

Divergens (Flukstetthet) Def - 2 D [3/3] D C A B

Divergens (Flukstetthet) Eks 1 - Fortegn - 2 D Ekspanderende gass i punktet (x 0, y 0) Komprimerende gass i punktet (x 0, y 0)

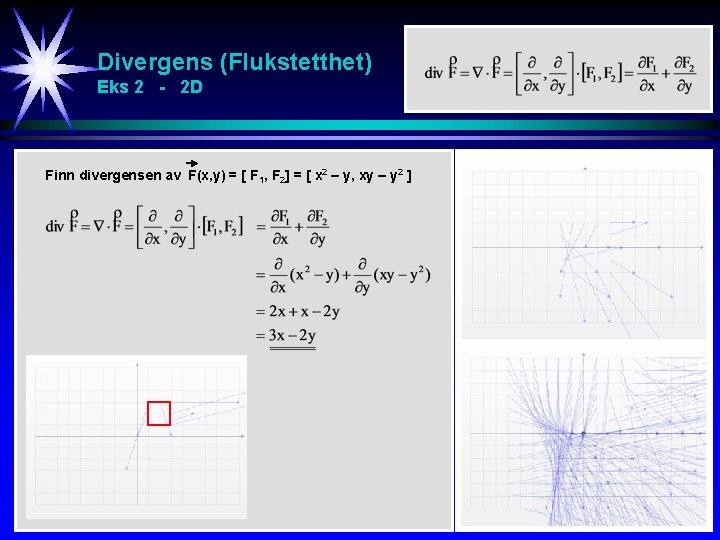
Divergens (Flukstetthet) Eks 2 - 2 D Finn divergensen av F(x, y) = [ F 1, F 2] = [ x 2 – y, xy – y 2 ]

Curl (Sirkulasjonstetthet) Def - 2 D [1/3]

Curl (Sirkulasjonstetthet) Def - 2 D [2/3]

Curl (Sirkulasjonstetthet) Def - 2 D [3/3] D C A B

Curl (Sirkulalsjonstetthet) Eks 1 - Fortegn - 2 D Rotasjon mot klokka i punktet (x 0, y 0) Rotasjon med klokka i punktet (x 0, y 0)

Divergens Curl (Flukstetthet (Sirkulasjonstetthet) C A Divergens n F Curl C A T F

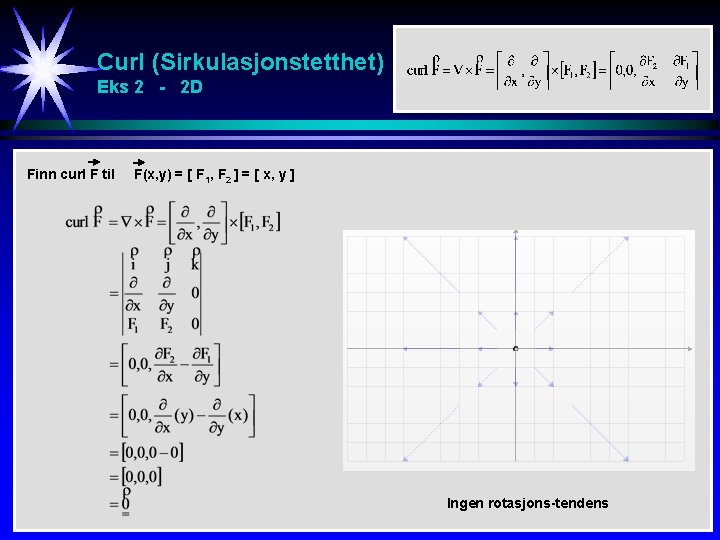
Curl (Sirkulasjonstetthet) Eks 2 - 2 D Finn curl F til F(x, y) = [ F 1, F 2 ] = [ x, y ] Ingen rotasjons-tendens

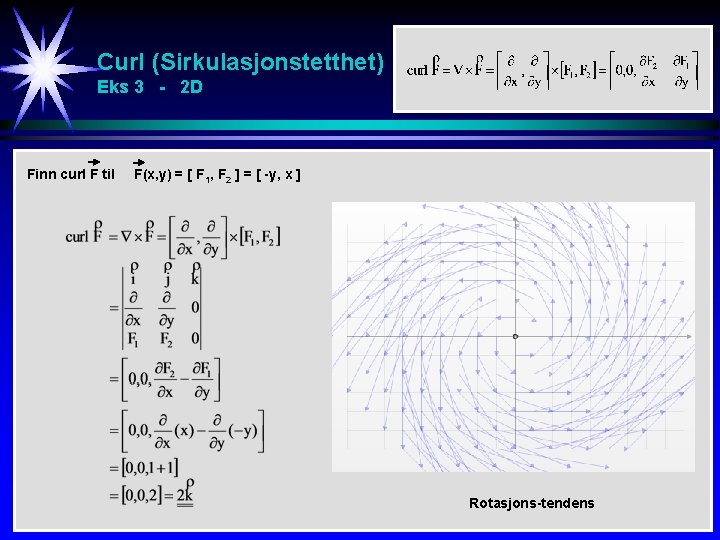
Curl (Sirkulasjonstetthet) Eks 3 - 2 D Finn curl F til F(x, y) = [ F 1, F 2 ] = [ -y, x ] Finn k-komponenten av curl til F(x, y) = [ M, N] = [ x 2 – y, xy – y 2 ] Rotasjons-tendens

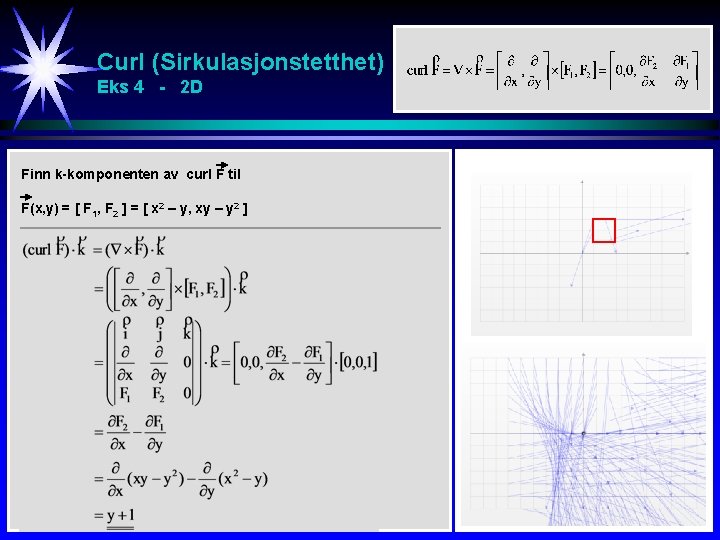
Curl (Sirkulasjonstetthet) Eks 4 - 2 D Finn k-komponenten av curl F til F(x, y) = [ F 1, F 2 ] = [ x 2 – y, xy – y 2 ]

Curl (Sirkulasjonstetthet) Fysisk tolkning av curl - 2 D R C k T F curl F er arbeid pr enhetsareal der F er bidraget til en rotasjon rundt randen til R. curl F peker rett opp når arbeidet er positivt, rett ned når arbeidet er negavivt. curl F sier noe om kraftfeltets tendens til å gi rotasjon (styrke og retning) i et gitt punkt.

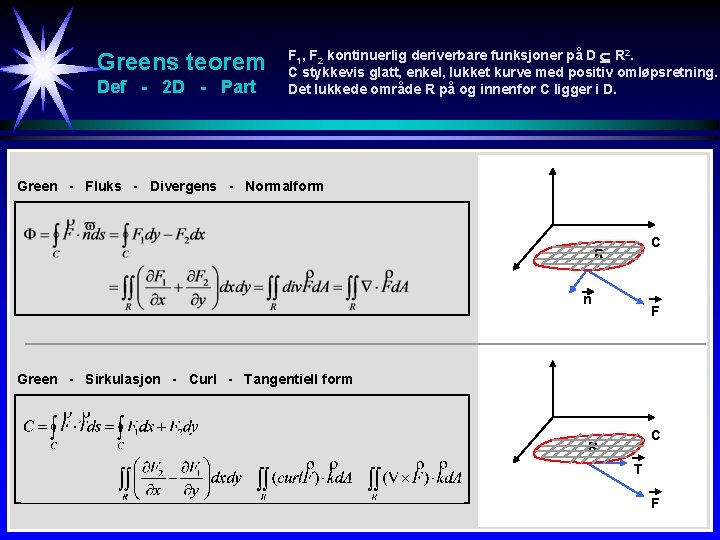
Greens teorem Def - 2 D Fluks - Divergens - Normalform Sirkulasjon - Curl - Tangentiell form F 1, F 2 kontinuerlig deriverbare funksjoner på D R 2. C stykkevis glatt, enkel, lukket kurve med positiv omløpsretning. Det lukkede område R på og innenfor C ligger i D.

Greens teorem Def - 2 D - Fig F 1, F 2 kontinuerlig deriverbare funksjoner på D R 2. C stykkevis glatt, enkel, lukket kurve med positiv omløpsretning. Det lukkede område R på og innenfor C ligger i D. Green - Fluks - Divergens - Normalform C R n F Green - Sirkulasjon - Curl - Tangentiell form C R T F

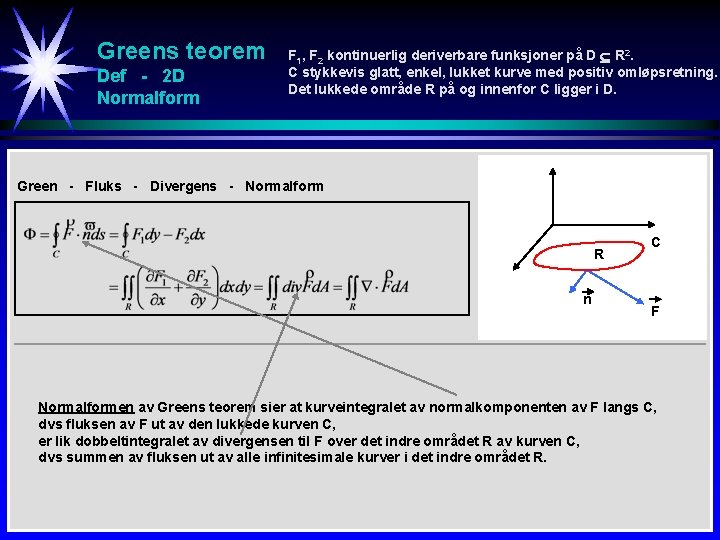
Greens teorem Def - 2 D Normalform F 1, F 2 kontinuerlig deriverbare funksjoner på D R 2. C stykkevis glatt, enkel, lukket kurve med positiv omløpsretning. Det lukkede område R på og innenfor C ligger i D. Green - Fluks - Divergens - Normalform R n C F Normalformen av Greens teorem sier at kurveintegralet av normalkomponenten av F langs C, dvs fluksen av F ut av den lukkede kurven C, er lik dobbeltintegralet av divergensen til F over det indre området R av kurven C, dvs summen av fluksen ut av alle infinitesimale kurver i det indre området R.

Greens teorem Def - 2 D Tangentiellform F 1, F 2 kontinuerlig deriverbare funksjoner på D R 2. C stykkevis glatt, enkel, lukket kurve med positiv omløpsretning. Det lukkede område R på og innenfor C ligger i D. Green - Sirkulasjon - Curl - Tangentiell form C R T F Tangentiellformen av Greens teorem sier at kurveintegralet av tangentiellkomponenten av F langs C, dvs sirkulasjonen av F langs den lukkede kurven C, er lik dobbeltintegralet av k-komponenten til curlen til F over det indre området R av kurven C, dvs summen av sirkulasjonen langs alle infinitesimale kurver i det indre området R.

Greens teorem Def - 2 D - Part F 1, F 2 kontinuerlig deriverbare funksjoner på D R 2. C stykkevis glatt, enkel, lukket kurve med positiv omløpsretning. Det lukkede område R på og innenfor C ligger i D. Green - Fluks - Divergens - Normalform C R n F Green - Sirkulasjon - Curl - Tangentiell form C R T F

Greens teorem Bevis-skisse - Curl / Div - 2 D y C Ci, j+1 III Ci+1, j+1 IV RP Ci, j x Ri, j Ci+1, j Ri, j I II

Greens teorem Bevis-skisse - Curl - 2 D y C x III IV Ri, j I II

Greens teorem Bevis-skisse - Div - 2 D y C x III IV Ri, j I II

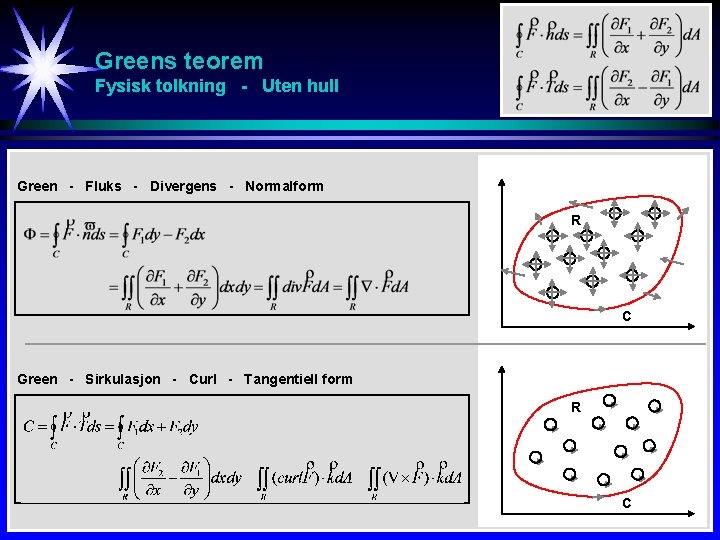
Greens teorem n hull Fysisk tolkning - Uten hull Green - Fluks - Divergens - Normalform R C Green - Sirkulasjon - Curl - Tangentiell form R C

Positiv og negativ fluks Def - 2 D - Fig Green - Fluks - Divergens - Normalform Flom Positiv fluks Uttapping av vann Negativ fluks Elektrisk felt Positiv fluks / Negativ fluks Elektrisk felt Null fluks E

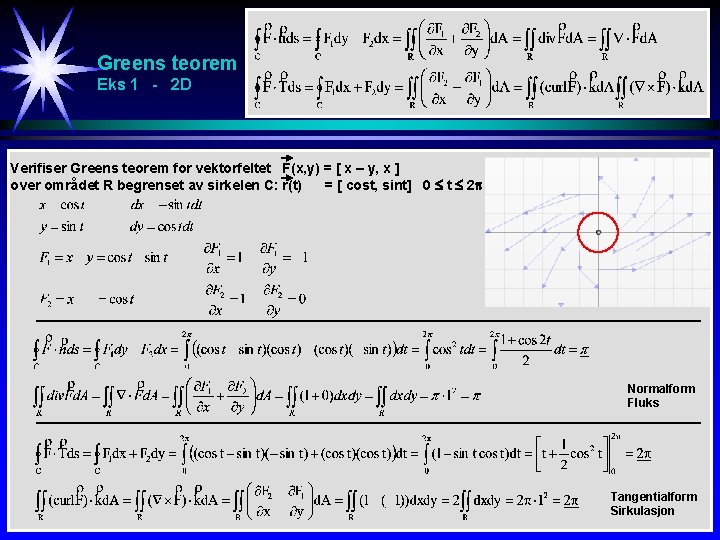
Greens teorem Eks 1 - 2 D Verifiser Greens teorem for vektorfeltet F(x, y) = [ x – y, x ] over området R begrenset av sirkelen C: r(t) = [ cost, sint] 0 t 2 Normalform Fluks Tangentialform Sirkulasjon

Greens teorem Områder med hull - 2 D [1/2] C 1 y R x C 1 y R 1 C 2 A J 2 R 2 C 22 J 1 C 12 x C 11 B

Greens teorem Områder med hull - 2 D [2/2] y C 1 R 1 C 21 J 2 R 2 C 11 C 2 J 1 C 22 1 hull C 12 x y C R C 1 C 3 C 2 x n hull

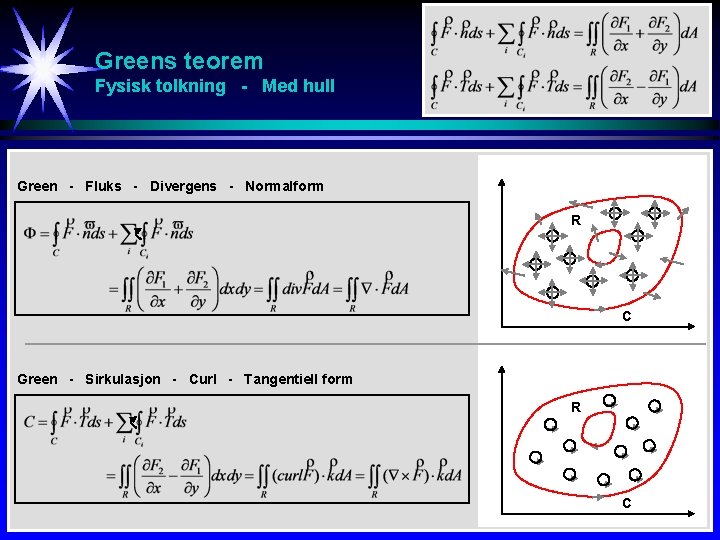
Greens teorem n hull Fysisk tolkning - Med hull Green - Fluks - Divergens - Normalform R C Green - Sirkulasjon - Curl - Tangentiell form R C

Greens teorem Områder med hull - Eks - 2 D [1/3] y C Ca x

Greens teorem Områder med hull - Eks - 2 D [2/3] y C Ca x

Greens teorem Områder med hull - Eks - 2 D [3/3] y C Ca x

Greens teorem Eks - 2 D [1/4] Uten Greens teorem y 1 III C II IV I 1 x

Greens teorem Eks - 2 D [2/4] Med Greens teorem (normal/tangential) y 1 III I tillegg til direkte beregning, kan integralet beregnes vha Greens teorem, enten vha fluks- eller sirkulasjons-betraktninger. C II IV I 1 x Fluks F = [ xy, y 2 ] Sirkulasjon F = [ -y 2, xy ]

Greens teorem Eks - 2 D [3/4] Normalform y 1 III C II IV I 1 x

Greens teorem Eks - 2 D [4/4] Tangentiellform y 1 III C II IV I 1 x

Greens teorem Eks - Kurve C [1/4] Tangentiellform Bestem hvilken lukket kurve C orientert i positiv retning (mot klokka) i planet som gir minimumsverdi av følgende integral: C 2 C 1 C 3

Greens teorem Eks - Kurve C [2/4] Tangentialform R 2 C 1 R 3 C 3

Greens teorem Eks - Kurve C [3/4] Tangentialform Siden integranden i dobbeltintegralet over R er null på ellipsen C, positiv utenfor ellipsen C og negativ innenfor ellipsen C, så vil dobbeltintegralet (summeringen) gi en minimum verdi når området R er området innenfor den gitte ellipsen C. R 2 Ellipsen C C 2 C 1 C R 1 R 3 C 3 R

Greens teorem Eks - Kurve C [4/4] Tangentialform Ellipsen C C C

Greens teorem Areal som sirkel-integral - Innledning Arealet av et område R i planet er gitt ved: y R C Vi skal se hvordan vi vha Greens teorem kan finne en formel for areal som enkelt sirkel-integral langs konturen av området. Det finnes uendelig mange slike formler. Dette betyr at det er mulig å bestemme arealet av et område ved å bevege seg rundt området når vi til enhver tid kjenner til hvor langt vi beveger oss og i hvilken retning vi beveger oss. x

Greens teorem Areal som sirkel-integral - Tangentiell form - Def 1 Greens teorem (tangentiell form): y Arealet av området R: Greens teorem (tangentiell form) beregner arealet av R hvis: Mulig løsning: R C x

Greens teorem Areal som sirkel-integral - Tangentiell form - Def 2 Greens teorem (tangentiell form): y Arealet av området R: Greens teorem (tangentiell form) beregner arealet av R hvis: Mulig løsning: R C x

Greens teorem Areal som sirkel-integral - Tangentiell form - Def 3 Greens teorem (tangentiell form): y Arealet av området R: Greens teorem (tangentiell form) beregner arealet av R hvis: Mulig løsning: R C x

Greens teorem Areal som sirkel-integral - Tangentiell form - Eks 1 Beregn arealet av et rektangel med sider a og b y b III C II IV I a x

Greens teorem Areal som sirkel-integral - Tangentiell form - Eks 2 Beregn arealet av en sirkel med radius a y C a x

Flate-integral Areal - Def f S beskrevet av nivåflaten f(x, y, z) = c z Planområdet R er projeksjonen av S (på figuren projeksjonen ned i xy-planet) S p enhetsnormalvektor på planområdet R p R x y Arealet av S er gitt ved:

Flate-integral Areal - Bevis [1/2] S P R Q p P’ S’ A Q’ R’ PQRS parallellogram p enhetsnormalvektor på flaten A

Flate-integral Areal - Bevis [2/2] f p p S Ak R Pk Ak

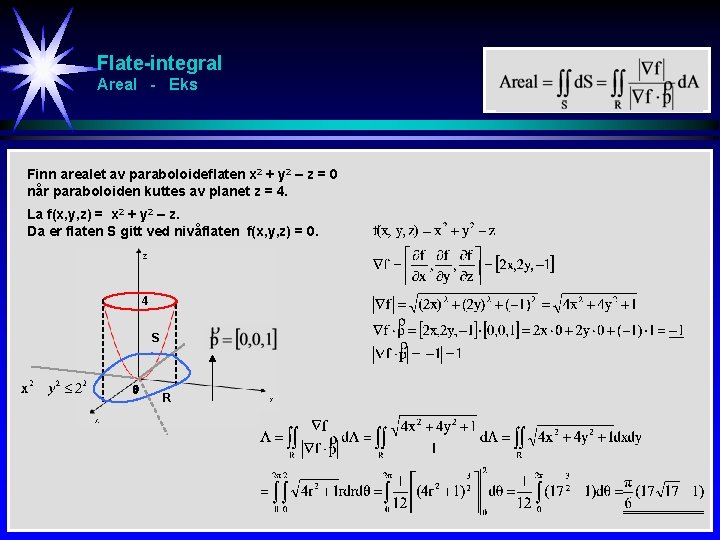
Flate-integral Areal - Eks Finn arealet av paraboloideflaten x 2 + y 2 – z = 0 når paraboloiden kuttes av planet z = 4. La f(x, y, z) = x 2 + y 2 – z. Da er flaten S gitt ved nivåflaten f(x, y, z) = 0. 4 S R

Flate-integral Areal - Spesialtilfeller Flate z = f(x, y) La F(x, y, z) = z – f(x, y) S er da gitt ved nivåflate F(x, y, z) = 0 4 S R

Flate-integral Def f d. S S p d. A R S g R p Flate gitt ved f(x, y, z) = c Kontinuerlig funksjon på S Projeksjonen av S Enhetsnormal på R

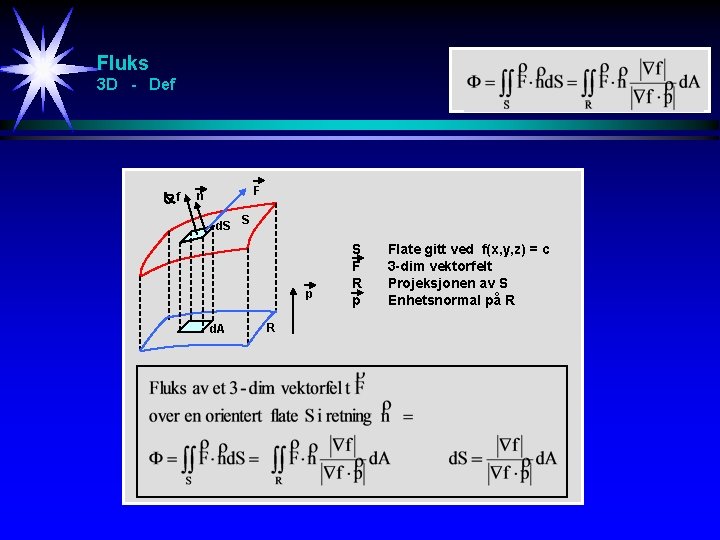
Fluks 3 D - Def f F n d. S S p d. A R S F R p Flate gitt ved f(x, y, z) = c 3 -dim vektorfelt Projeksjonen av S Enhetsnormal på R

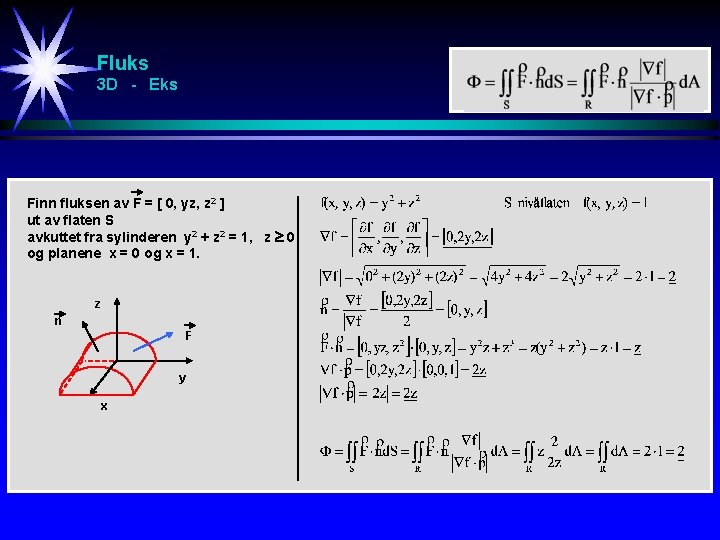
Fluks 3 D - Eks Finn fluksen av F = [ 0, yz, z 2 ] ut av flaten S avkuttet fra sylinderen y 2 + z 2 = 1, z 0 og planene x = 0 og x = 1. z n F y x

Masse, moment og massesenter til tynne skall Def Masse Moment Massesenter Treghetsmoment Gyrasjonsradius

Massesenter til tynne skall Eks Finn massesenteret til et tynt halvkuleskall med radius a og konstant massetetthet . z S R x y

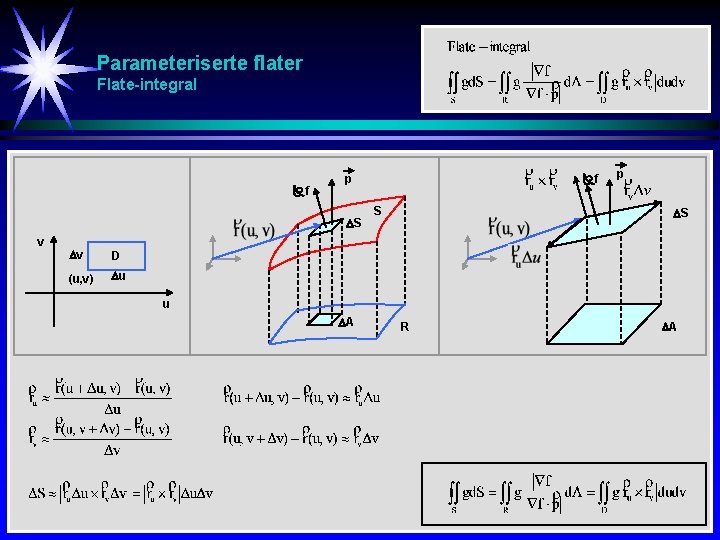
Parameteriserte flater Kurve Def Flate z a [ b C r(t) y ] t x z v S r(u, v) u y x

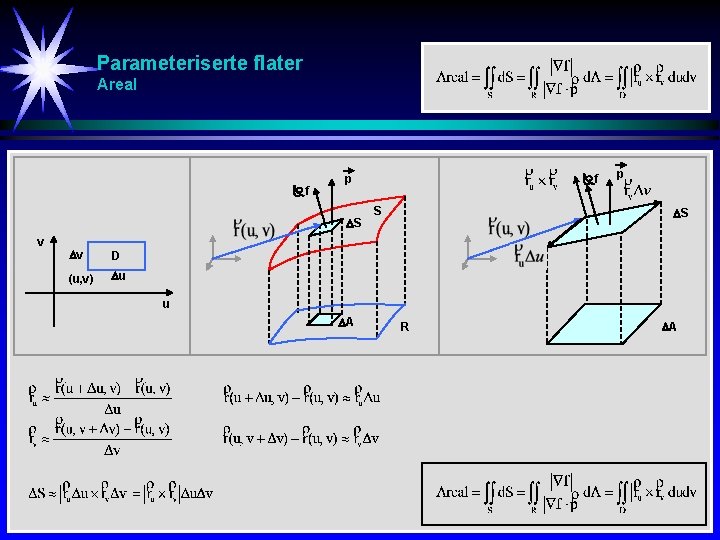
Parameteriserte flater Areal f S v v D (u, v) u f p S u A R A

Parameteriserte flater Flate-integral f S v v D (u, v) u f p S u A R A

Parameteriserte flater Flate-integral - Spesialtilfeller - Def Kartesiske koordinater Sylinder-koordinater Kule-koordinater

Parameteriserte flater Eks 1 - Kjegle z 1 r(t) S y x

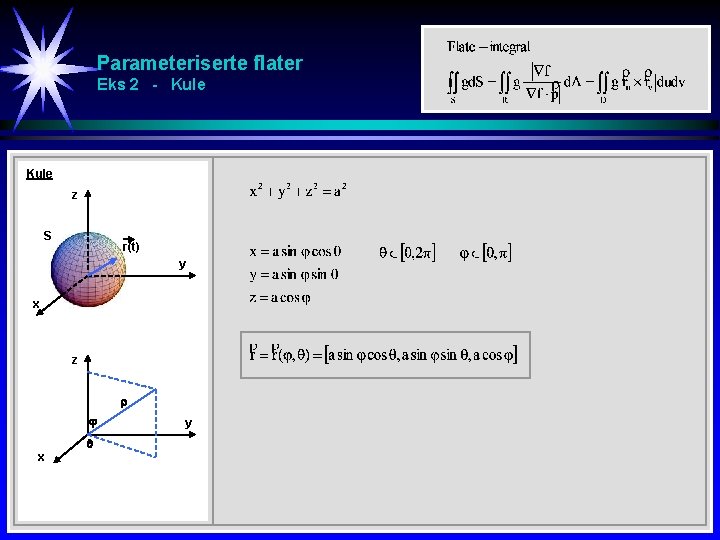
Parameteriserte flater Eks 2 - Kule z S r(t) y x z x y

Parameteriserte flater Eks 3 - Sylinder z S r(t) y x z S r(t) x 3 y

Parameteriserte flater Eks 4 Areal av kjegleflate [1/4] Kjegle Beregn arealet av kjegleflaten 1 Nivåflate z 2 Spesialtilfelle 1 r(t) S y x 3 Parameterisering

Parameteriserte flater Eks 4 Areal av kjegleflate [2/4] Kjegle 1 Nivåflate z 1 r(t) S y x

Parameteriserte flater Eks 4 Areal av kjegleflate [3/4] Kjegle 2 Spesialtilfelle z 1 r(t) S y x

Parameteriserte flater Eks 4 Areal av kjegleflate [4/4] Kjegle 3 Parameterisering z 1 r(t) S y x

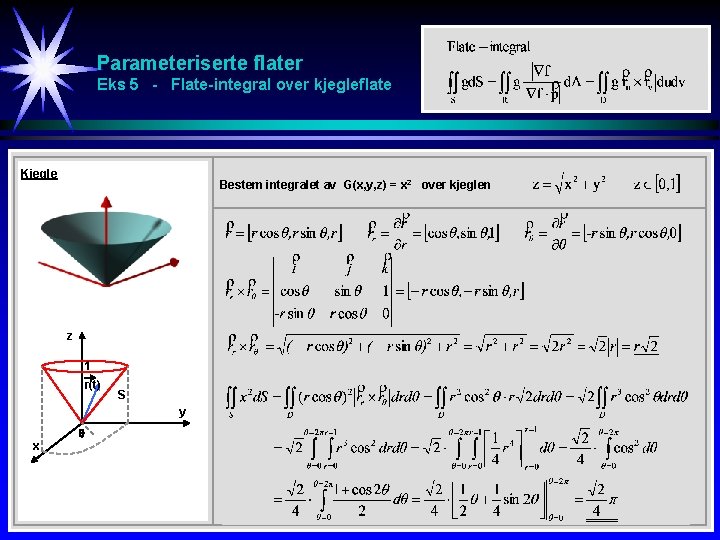
Parameteriserte flater Eks 5 - Flate-integral over kjegleflate Kjegle Bestem integralet av G(x, y, z) = x 2 over kjeglen z 1 r(t) S y x

Green - Div Greens teorem Def - 2 D Green - Curl Green - Fluks - Divergens - Normalform C R n F Green - Sirkulasjon - Curl - Tangentiell form C R T F

Gauss / Stokes teorem Def - 3 D - Div Stokes - Curl Gauss - Divergens z S n D F y x Stokes - Curl n z S C T F x y

Gauss / Stokes teorem Bevis-skisse Gauss - 3 D - Div Stokes - Curl z S n D F y x St Sb

Gauss / Stokes teorem Bevis-skisse Stokes - 3 D - Div Stokes - Curl n z S C T F y x E A D B C

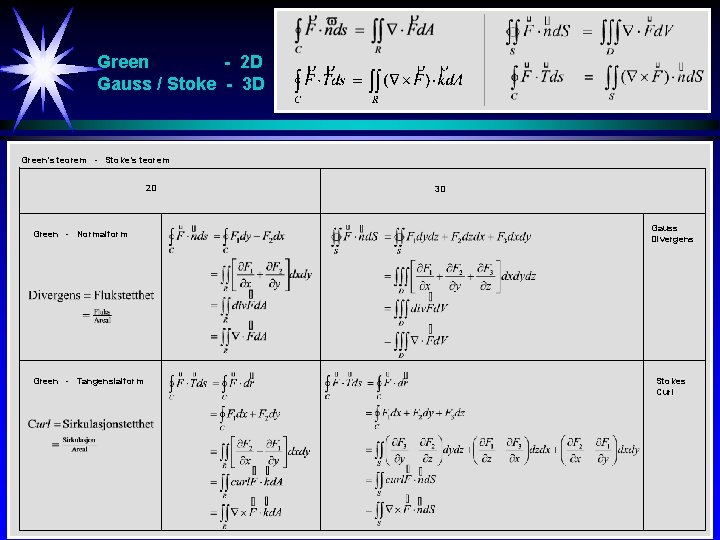
Green - 2 D Gauss / Stoke - 3 D Green’s teorem - Stoke’s teorem 2 D 3 D Gauss Divergens Green - Normalform Stoke Green - Tangensialform Stokes Curl

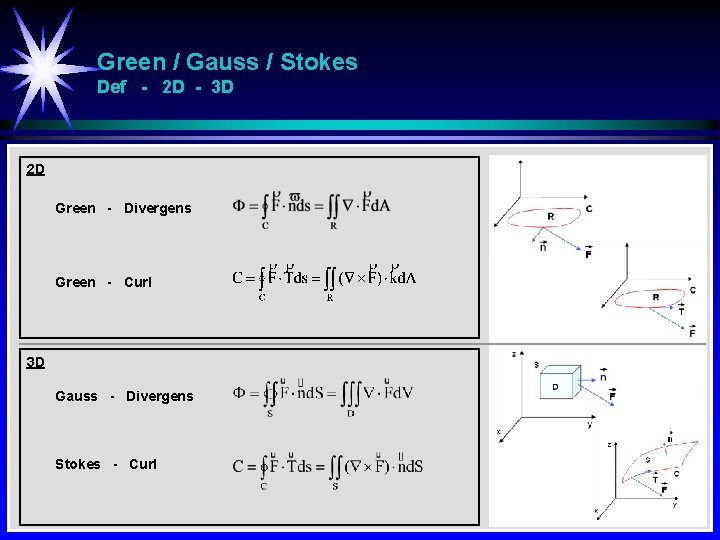
Green / Gauss / Stokes Def - 2 D - 3 D 2 D Green - Divergens Green - Curl 3 D Gauss - Divergens Stokes - Curl

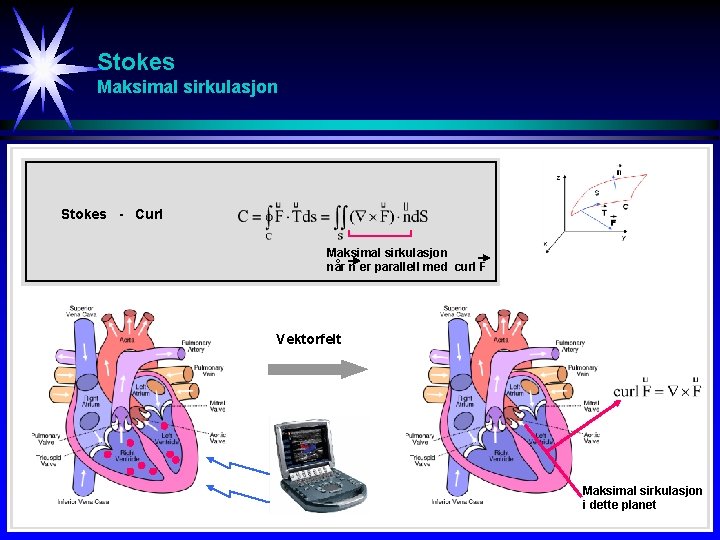
Stokes Maksimal sirkulasjon Stokes - Curl Maksimal sirkulasjon når n er parallell med curl F Vektorfelt Maksimal sirkulasjon i dette planet

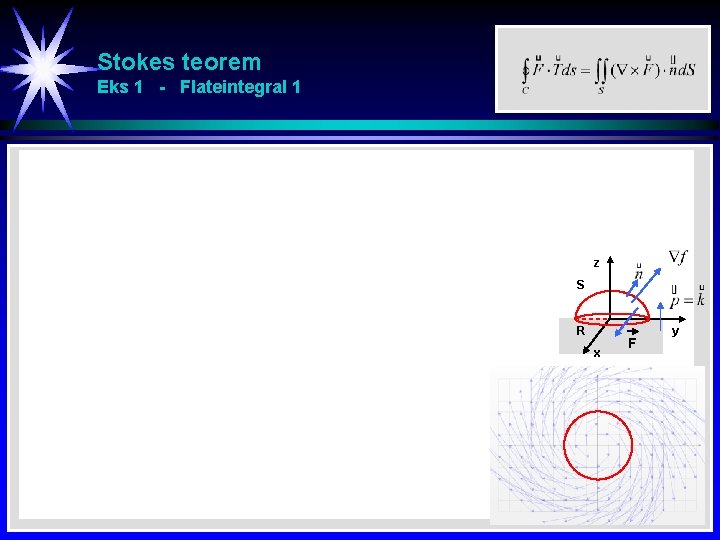
Stokes teorem Eks 1 - Verifisering Verifiser (kontroller) Stokes teorem for en halvkule med følgende data: Vektorfelt : F = [ y, -x, 0 ] Kuleflate : S : x 2 + y 2 + z 2 = 9 z 0 2 2 Rand : C: x +y =9 z S C R x F y

Stokes teorem Eks 1 - Sirkulasjon Verifiser (kontroller) Stokes teorem for en halvkule med følgende data: Vektorfelt : F = [ y, -x, 0 ] Kuleflate : S : x 2 + y 2 + z 2 = 9 z 0 2 2 Rand : C: x +y =9 z S C R x F y

Stokes teorem Eks 1 - Flateintegral 1 z S C R x F y

Stokes teorem Eks 1 - Flateintegral 2 Velger S 2: x 2 + y 2 9 som ny flate. Også denne flaten har C som rand. z S C R S 2 x F y

Stokes teorem Eks 2 - Sirkulasjon Finn både direkte og vha Stokes teorem sirkulasjonen av F = [ x 2 -y, 4 z, x 2 ] langs (mot klokka) kurven C fremkommet ved skjæring av planet z = 2 med kjeglen z = x 2 + y 2 z C F 2 y x

Stokes teorem Eks 2 - Flateintegral 1 - S: Kjeglesideflate z 2 n S F y x

Stokes teorem Eks 2 - Flateintegral 2 - S: Kjegletoppflate n = [0, 0, 1] z S 2 F y x

Stokes teorem Eks 3 - Oppgave Bruk Stokes teorem til å beregne z (0, 0, 2) F C for F = [ xz, xy, 3 xz ] hvor C er randen av den delen av planet 2 x + y + z = 2 som befinner seg i første oktant og C gjennomløpes i retning mot klokka sett ovenfra. (0, 2, 0) (1, 0, 0) x y

Stokes teorem Eks 3 - Løsning z (0, 0, 2) F C (1, 0, 0) x n (0, 2, 0) y

Gauss teorem Eks 1 z Kontroller Gauss teorem (divergens-teoremet) for F = [ x, y, z ] over kula x 2 + y 2 + z 2 = a 2. F S a n y x

Gauss teorem Eks 2 z Finn fluksen av F = [ xy, yz, xz ] ut av kubus-flaten i første oktant begrenset av planene x = 1, y = 1 og z = 1. S F D x n y

Gauss teorem Eks 2 - Alternativ: Symmetri z Finn fluksen av F = [ xy, yz, xz ] ut av kubus-flaten i første oktant begrenset av planene x = 1, y = 1 og z = 1. S F D x Symmetriegenskaper n y

END