VEDIC MATHEMATICS Digital RootsSums T K Prasad http

VEDIC MATHEMATICS : Digital Roots/Sums T. K. Prasad http: //www. cs. wright. edu/~tkprasad Prasad Digital Roots 1

Definition • Digital root of a number is the single digit obtained by repeatedly summing all the digits of a number. • Example: • Digital root of 2357 = 8 because (2 + 3 + 5 + 7 = 17) and (1 + 7 = 8) • Digital root of 89149 = 4 because (8 + 9 + 1 + 4 + 9 = 31) and (3 + 1 = 4) Prasad Digital Roots 2

Some facts we already know • A number is divisible by 3 if its digital root is divisible by 3 (that is, it is 0, 3, 6, or 9). • 1236 is divisible by 3 because 3 is divisible by 3. • Note (1+2+3+6 = 12) and (1+2 = 3). • Recall: 1 x(999+1) + 2 x(99+1) + 3 x(9+1) + 6 • A number is divisible by 9 if its digital root is divisible by 9 (that is, it is 0 or 9). Prasad Digital Roots 3

(cont’d) • The digital root of a number is the remainder obtained by dividing it by 9. • 1236 divided by 9 = … R 3 • Recall: 1 x(999+1) + 2 x(99+1) + 3 x(9+1) + 6 • Note that 9 is treated similar to 0. • 36 divided by 9 = … R 0 Prasad Digital Roots 4

(cont’d) • Digital roots can be calculated quickly by casting out 9 s. • 12173645 => (1+2+1+7+3+6+4+5) = (2+9) = (1+1) = 2 • 12173645 => (1+1)=2 Prasad Digital Roots 5

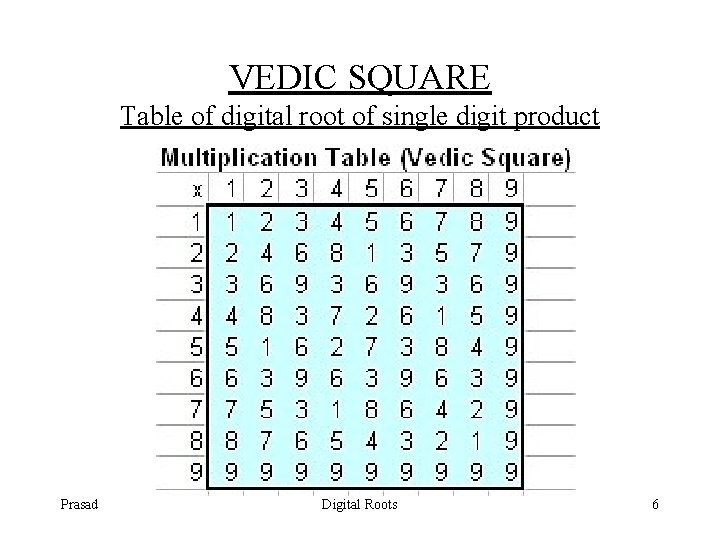
VEDIC SQUARE Table of digital root of single digit product Prasad Digital Roots 6

9 point circle Prasad Digital Roots 7

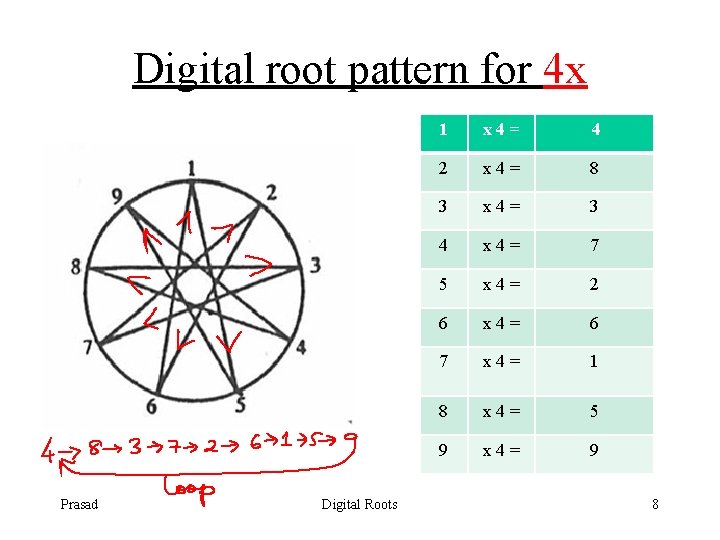
Digital root pattern for 4 x Prasad Digital Roots 1 x 4= 4 2 x 4= 8 3 x 4= 3 4 x 4= 7 5 x 4= 2 6 x 4= 6 7 x 4= 1 8 x 4= 5 9 x 4= 9 8

Properties of digital roots • Digital root of a square is 1, 4, 7, or 9 • Digital root of a perfect cube is 1, 8 or 9 • Digital root of a prime number (except 3) is 1, 2, 4, 5, 7, or 8 • Digital root of a power of 2 is 1, 2, 4, 5, 7, or 8 Prasad Digital Roots 9

Justification for digital roots of a prime number • Recall that digital root of 3, 6, or 9 implies it is divisible by 3. • The digital root of 1, 2, 4, 5, 7, and 8 are realizable by the prime numbers 19, 2 (11), 13, 5 (23), 7 (43), and 8 (17), respectively. – This is a necessary (but not sufficient) condition for a number to be prime. Prasad Digital Roots 10

Additive Persistence of a Number • Additive persistence of a number is the number of steps required to reach the digital root. • Additive persistence of 52 = One, because (5 + 2) =One=> (7) • Additive persistence of 5243 = Two, because (5 + 2 + 4 + 3) =One=> (14) =Two=> (5) Prasad Digital Roots 11

(cont’d) • The smallest number for additive persistence 0 through 4 are: 0 step => 0 1 step => 10 2 steps => 19 3 steps => 199 4 steps => 19999999999999999999999 Prasad Digital Roots 12

(cont’d) 0 step => 0 1 step => 10 2 steps => 19 (quotient 19 -1 divide 9 = 2 ) 3 steps => 199 (2 9’s + 1) (quotient 199 -1 divide 9 = 22) 4 steps => 199999999999 (22 9’s + 1) Hint: It is the number of 9’s we add to get (the previous number in the sequence – 1)? Prasad Digital Roots 13

(cont’d) 4 steps => 199999999999 (22 9’s + 1) 5 steps => 1 followed by (quotient 1999999999998 divide 9) 9’s => 1 followed by 22222222222 9’s Prasad Digital Roots 14

How big is the last number? • Larger than the number of stars in the universe? • 10^21 (10 followed by 21 zeros) • YES. • Larger than the number of atoms in the universe? • 10^80 • YES. • Larger than googol 10^100? • YES. • Larger than googolplex 10 followed by 10^100 0’s? • NO, we have at last found a match! Prasad Digital Roots 15

Application: Parity and Checksum (Digression of sorts) • Bit (Binary Digit) : 0, 1 • Numbers in binary: 000, 001, 010, 011, 100, … • Numbers in decimal: 0, 1, 2, 3, 4, … Prasad Digital Roots 16

Parity • Parity bit is added to ensure that the number of 1 bits in a given set or sequence of bits is always even or odd. • Odd parity: 000 1, 001 0, 011 1, 100 0, etc • Even parity: 000 0, 001 1, 011 0, 100 1, etc • Parity is used to detect single bit errors in transmission. Prasad Digital Roots 17

Check digit (Checksum) • Check digit is single digit computed from the digits of a number (usually representing a short message or identifying an object). • Check digit (or more generally checksum) is used to detect errors (in message transmission or storage). Prasad Digital Roots 18

(cont’d) • E. g. , The final digit in UPC code (barcode) for products, ISBN number for books, etc are a form of check digit. • E. g. , Credit card numbers use check digits. • E. g. , Message/Data encoding techniques (for storing information on devices such as hard disk, CD, DVD, etc or transmitting information over the wire or by wireless means) use sophisticated checksums. Prasad Digital Roots 19

Appendix : Dr. Scheme Code Prasad Digital Roots 20

; ; (accumulate + 0 (1 2 13 4)) = 0 + 1 + 2 + 13 + 4 = 20 (define (accumulate f id lis) (if (null? lis) id (f (car lis) (accumulate f id (cdr lis))) ) ) (accumulate + 0 '(1 2 3 8 9 0)) "should be" Prasad Digital Roots 23 21

; ; DEFINITION: Digital sum/root of a number is obtained by ; ; repeatedly summming its digits or of the sum so obtained ; ; till it reduces to a single digit. ; ; digital. Root takes a number n >= 0 and returns its digital sum/root ; ; DEFINITION: Additive persistance of a number is the number of ; ; steps it takes to reduce the number to its digital sum/root. ; ; add-persist takes a number n >= 0 and returns its additive persistence. Prasad Digital Roots 22

(define (digital. Root n) (if (<= 0 n 9) n (digital. Root (accumulate + 0 (map (lambda (d) (- d 48)) (map char->integer (string->list (number->string n))) )) (digital. Root 10) "should be" 1 (digital. Root 1237890) "should be" 3 Prasad Digital Roots 23

(define (add-persist n) (if (<= 0 n 9) 0 (+ 1 (add-persist (digital. Root n)) ) (add-persist 9) "should be" 0 (add-persist 10) "should be" 1 (add-persist 1237890) "should be" 3 Prasad Digital Roots 24

; ; nines takes an number n > 0 and returns a number with n 9 s (define (nines n) (if (eq? n 1) 9 (+ 9 (* (nines (- n 1)) 10)) ) ) (nines 1) "should be" 9 (nines 10) "should be" 99999 Prasad Digital Roots 25

; ; Recall, additive persistance of a number is the number of steps ; ; it takes to reduce the number to its digital sum/root. ; ; min-add-persist takes an number n >= 0 and ; ; returns the smallest number with additive persistence of n ; ; LOGIC: To get min-add-persist of n, take the largest number with ; ; additive persistance of (n-1) and generate a string of 9 s that ; ; add upto it, and then prepend it with 1, to get the smallest number ; ; that overflows addtive persistance of n. Prasad Digital Roots 26

(define (min-add-persist n) (cond ((eq? n 0) 0) ((eq? n 1) 10) (else (let ((max-prev (quotient (- (min-add-persist (- n 1)) 1) 9))) (+ (expt 10 max-prev) (nines max-prev))) ) (map min-add-persist '(0 1 2 3 4)) “should be” (0 10 19 1999999999999) (add-persist (min-add-persist 4)) "should be" 4 (add-persist (- (min-add-persist 4) 1)) "should be" 3 Prasad Digital Roots 27

Interesting Case! (min-add-persist 5) ; Number of 9 s in this number is ; (quotient 1999999999998 9) ; which is 22 2’s, that is, 22222 22 ; Total number of atoms in the universe is ; only 80 digits long! ; Googol = 10^100 ; Googolplex = 10^(10^100) Prasad Digital Roots 28