VectorValued Functions Section 10 3 a Standard Unit







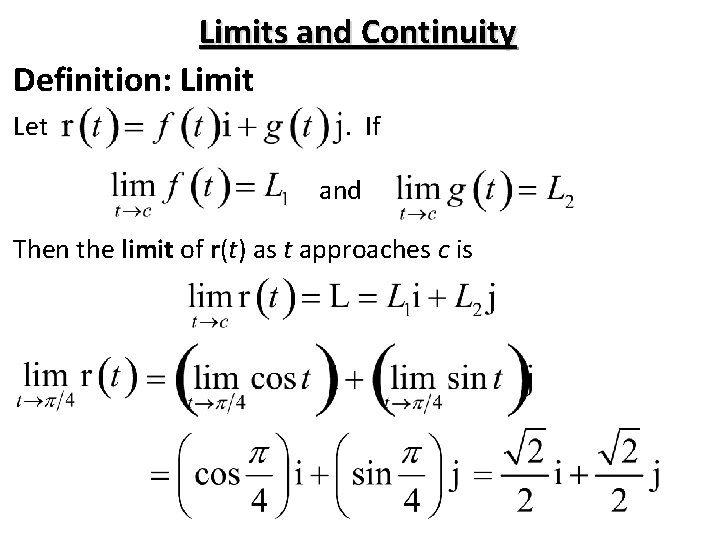













- Slides: 22

Vector-Valued Functions Section 10. 3 a

Standard Unit Vectors Any vector in the plane can be written as a linear combination of the two standard unit vectors: as follows: The vector v is a linear combination of the vectors i and j; the scalar a is the horizontal component of v and the scalar b is the vertical component of v: bj v ai

Standard Unit Vectors Any vector in the plane can be written as a linear combination of the two standard unit vectors: as follows: Quick Practice: Given P(– 1, 5) and Q(3, 2), write the following vector as a linear combination of i and j: Component form: As a linear combination…

Planar Curves When a particle moves through the plane during a time interval I, we think of the particle’s coordinates as functions defined on I: The points , make up the curve in the plane that is the particle’s path. The equations and interval in the equation above parametrize the curve. The vector from the origin to the particle’s position at time t is the particle’s position vector. The functions f and g are the component functions (components) of the position vector. we think of the particle’s path as the curve traced by r during the time interval I.

Planar Curves In the next example, r is defined as a vector function of the real variable t on the interval I. More generally, a vector function or vector-valued function on a domain D is a rule that assigns a vector in the plane to each element in D. The curve traced by a vector function is its graph. We refer to real-valued functions as scalar functions to distinguish them from vector functions. The components of r are scalar functions of t. When we define a vector-valued function by giving its component functions, we assume the vector function’s domain to be the common domain of the components.

Planar Curves Graph the vector function We can graph parametrically using Window settings: Tmin = 0, Tmax = 50, Tstep = 0. 1, Xmin = – 30, Xmax = 30, Xscl = 1, Ymin = – 20, Ymax = 20, Yscl = 1 As the curve graphs, imagine how this curve is being defined as traced by a changing vector…

Limits and Continuity Definition: Limit Let . If and Then the limit of r(t) as t approaches c is Another quick example: If , then
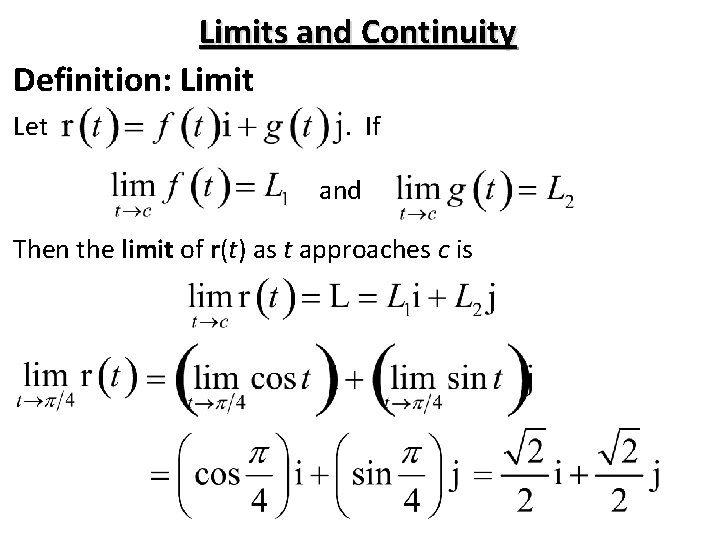
Limits and Continuity Definition: Limit Let . If and Then the limit of r(t) as t approaches c is

Limits and Continuity Definition: Continuity at a Point A vector function r(t) is continuous at a point t = c in its domain if A vector function r(t) is continuous if it is continuous at every point in its domain. Component Test for Continuity at a Point The vector function is continuous at t = c if and only if f and g are continuous at t = c.

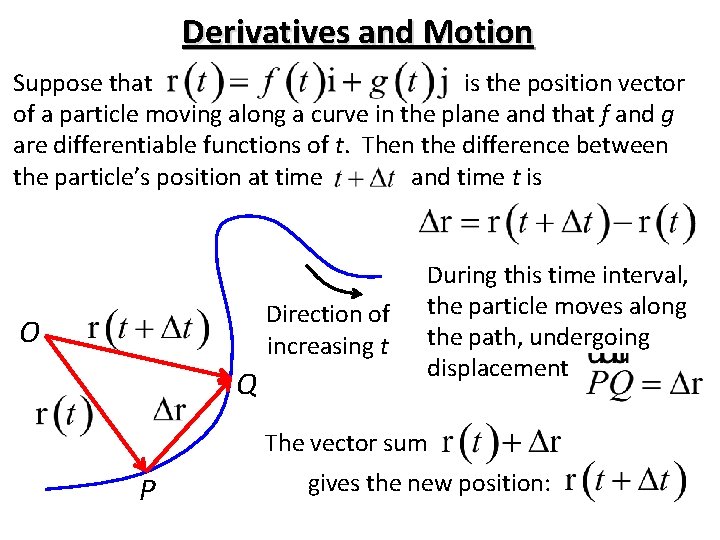
Derivatives and Motion Suppose that is the position vector of a particle moving along a curve in the plane and that f and g are differentiable functions of t. Then the difference between the particle’s position at time and time t is Direction of increasing t O Q During this time interval, the particle moves along the path, undergoing displacement The vector sum P gives the new position:

Derivatives and Motion Suppose that is the position vector of a particle moving along a curve in the plane and that f and g are differentiable functions of t. Then the difference between the particle’s position at time and time t is Written in terms of components… Now, what happens as approaches zero? ? ?

Derivatives and Motion Now, what happens as approaches zero? ? ? 1. Q approaches P along the curve. Direction of increasing t O Q P 3. The quotient following limit: 2. The secant line PQ seems to approach a limiting position tangent to the curve at P. approaches the

Derivatives and Motion Now, what happens as 3. The quotient approaches zero? ? ? approaches the following limit: Do these limits look familiar? ? ?

Derivatives and Motion Definition: Derivative at a Point The vector function has a derivative (is differentiable) at t if f and g have derivatives at t. The derivative is the vector A vector function r is differentiable if it is differentiable at every point of its domain. The curve traced by r is smooth if dr/dt is continuous and never 0, that is, if f and g have continuous first derivatives that are not simultaneously zero. On a smooth curve there are no sharp corners or cusps.

Derivatives and Motion Definitions: Velocity, Speed, Acceleration, Direction of Motion If r is the position vector of a particle moving along a smooth curve in the plane, then at any time t, 1. is the particle’s velocity vector and is tangent to the curve. 2. , the magnitude of velocity, is the particle’s speed.

Derivatives and Motion Definitions: Velocity, Speed, Acceleration, Direction of Motion If r is the position vector of a particle moving along a smooth curve in the plane, then at any time t, 3. , the derivative of velocity and the second derivative of position, is the particle’s acceleration vector. 4. , a unit vector, is the direction of motion. Velocity = = (speed)(direction)

Studying Motion The vector of a moving particle at time t. Find (a) the velocity and acceleration vectors. gives the position

Studying Motion The vector of a moving particle at time t. Find gives the position (b) the velocity, acceleration, speed, and direction of motion at Velocity: Acceleration:

Studying Motion The vector of a moving particle at time t. Find gives the position (b) the velocity, acceleration, speed, and direction of motion at Speed: Direction:

Studying Motion The vector of a moving particle at time t. Find (c) gives the position . Interpret this result graphically. If the dot product is zero, then the vectors are orthogonal (graphically, they are perpendicular). Let’s interpret all of these results with a graph on the calculator…

Studying Motion The vector gives the position of a moving particle at time t. (a) Write an equation for the line tangent to the path of the particle at the point where t = – 1. At the time in question: The line passes through (– 5, 11) and has slope – 9/12 = – 3/4:

Studying Motion The vector gives the position of a moving particle at time t. (b) Find the coordinates of each point on the path where the horizontal component of the velocity is 0. The horizontal component of velocity: Which equals zero when t = 0 and t = 1. Coordinates at t = 0: Coordinates at t = 1: Again, support these results graphically…