VectorValued Functions 11 1 11 2 11 3

Vector-Valued Functions 11. 1 11. 2 11. 3 11. 4 11. 5 11. 6 CHAPTER 11 VECTOR-VALUED FUNCTIONS THE CALCULUS OF VECTOR-VALUED FUNCTIONS MOTION IN SPACE CURVATURE TANGENT AND NORMAL VECTORS PARAMETRIC SURFACES © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 2

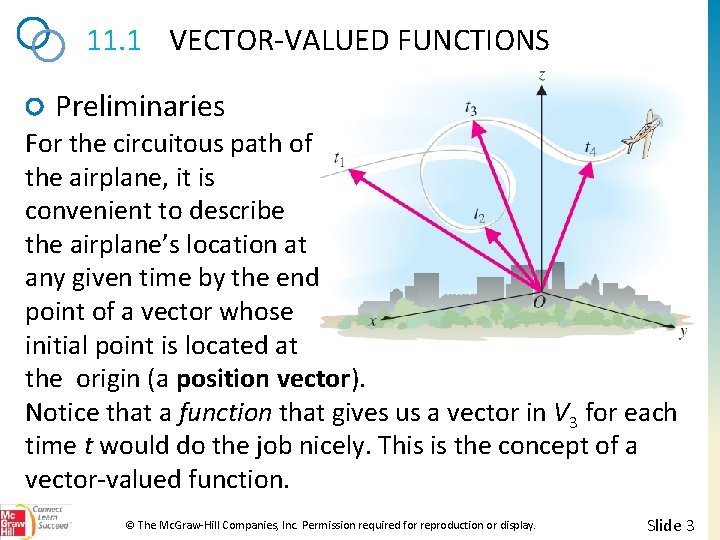
11. 1 VECTOR-VALUED FUNCTIONS Preliminaries For the circuitous path of the airplane, it is convenient to describe the airplane’s location at any given time by the end point of a vector whose initial point is located at the origin (a position vector). Notice that a function that gives us a vector in V 3 for each time t would do the job nicely. This is the concept of a vector-valued function. © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 3

11. 1 VECTOR-VALUED FUNCTIONS DEFINITION 1. 1 A vector-valued function r(t) is a mapping from its domain D ⊂ to its range R ⊂ V 3, so that for each t in D, r(t) = v for exactly one vector v ∈ R. We can always write a vector-valued function as r(t) = f (t)i + g(t)j + h(t)k, (1. 1) for some scalar functions f, g and h (called the component functions of r). We can likewise define a vector-valued function r(t) in V 2 by r(t) = f (t)i + g(t)j, for some scalar functions f and g. © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 4

11. 1 VECTOR-VALUED FUNCTIONS Preliminaries For each t, we regard r(t) as a position vector. The endpoint of r(t) then can be viewed as tracing out a curve. Observe that for r(t) as defined in (1. 1), this curve is the same as that described by the parametric equations x = f (t), y = g(t) and z = h(t). In three dimensions, such a curve is referred to as a space curve. © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 5

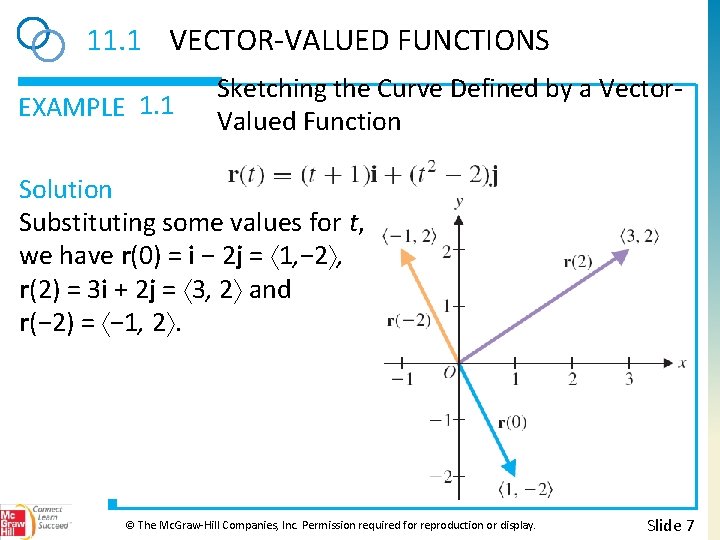
11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 1 Sketching the Curve Defined by a Vector. Valued Function Sketch a graph of the curve traced out by the endpoint of the two-dimensional vector-valued function r(t) = (t + 1)i + (t 2 − 2)j. © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 6

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 1 Sketching the Curve Defined by a Vector. Valued Function Solution Substituting some values for t, we have r(0) = i − 2 j = 1, − 2 , r(2) = 3 i + 2 j = 3, 2 and r(− 2) = − 1, 2. © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 7

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 1 Sketching the Curve Defined by a Vector. Valued Function Solution The endpoints of all position vectors r(t) lie on the curve C, described parametrically by Eliminate the parameter: © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 8

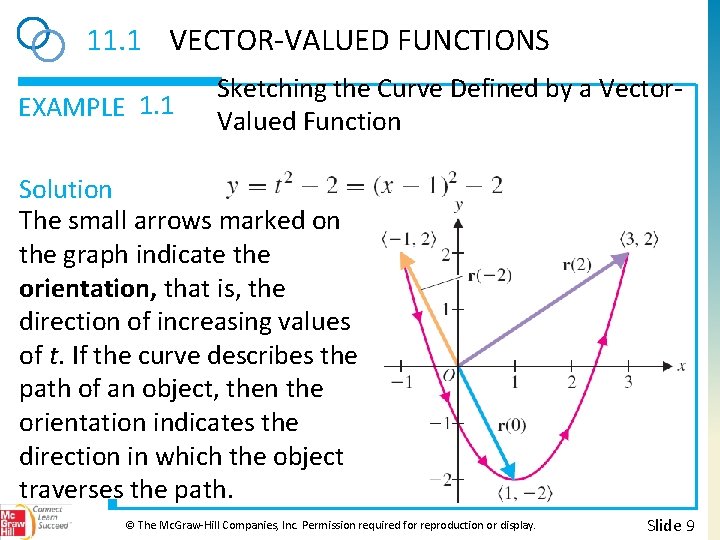
11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 1 Sketching the Curve Defined by a Vector. Valued Function Solution The small arrows marked on the graph indicate the orientation, that is, the direction of increasing values of t. If the curve describes the path of an object, then the orientation indicates the direction in which the object traverses the path. © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 9

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 2 A Vector-Valued Function Defining an Ellipse Sketch a graph of the curve traced out by the endpoint of the vector-valued function © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 10

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 2 A Vector-Valued Function Defining an Ellipse Solution © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 11

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 3 A Vector-Valued Function Defining an Elliptical Helix Plot the curve traced out by the vector-valued function r(t) = sin ti − 3 cos tj + 2 tk, t ≥ 0. © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 12

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 3 A Vector-Valued Function Defining an Elliptical Helix Solution © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 13

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 4 A Vector-Valued Function Defining a Line Plot the curve traced out by the vector-valued function © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 14

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 4 A Vector-Valued Function Defining a Line Solution Recognize these equations as parametric equations for the straight line parallel to the vector 2, − 3, − 4 and passing through the point (3, 5, 2). © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 15

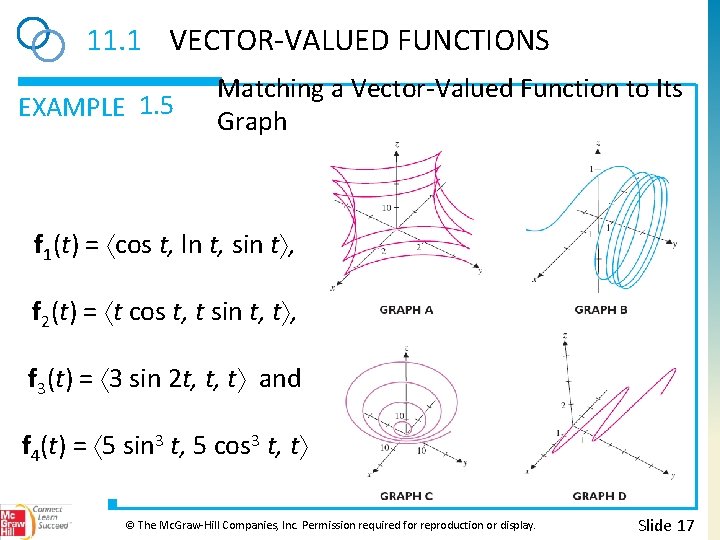
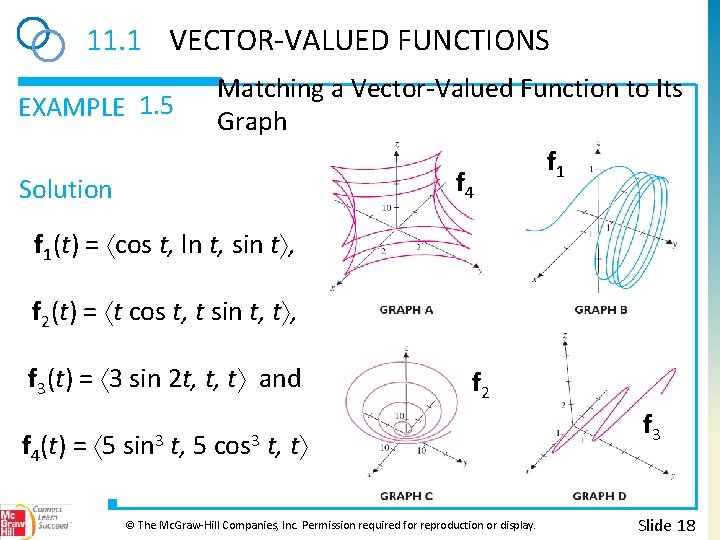
11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 5 Matching a Vector-Valued Function to Its Graph Match each of the vector-valued functions f 1(t) = cos t, ln t, sin t , f 2(t) = t cos t, t sin t, t , f 3(t) = 3 sin 2 t, t, t and f 4(t) = 5 sin 3 t, 5 cos 3 t, t with the corresponding computer-generated graph (on the following slide). © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 16

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 5 Matching a Vector-Valued Function to Its Graph f 1(t) = cos t, ln t, sin t , f 2(t) = t cos t, t sin t, t , f 3(t) = 3 sin 2 t, t, t and f 4(t) = 5 sin 3 t, 5 cos 3 t, t © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 17

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 5 Solution Matching a Vector-Valued Function to Its Graph f 1 f 4 f 1(t) = cos t, ln t, sin t , f 2(t) = t cos t, t sin t, t , f 3(t) = 3 sin 2 t, t, t and f 4(t) = 5 sin 3 t, 5 cos 3 f 2 t, t © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. f 3 Slide 18

11. 1 VECTOR-VALUED FUNCTIONS Arc Length in A natural question to ask about a curve is, “How long is it? ” Note that the plane curve traced out exactly once by the endpoint of the vector-valued function r(t) = f (t), g(t) , for t ∈ [a, b] is the same as the curve defined parametrically by x = f (t), y = g(t). Recall from section 10. 3 that if f, f' , g and g' are all continuous for t ∈ [a, b], the arc length is given by © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 19

11. 1 VECTOR-VALUED FUNCTIONS Arc Length in Consider a space curve traced out by the endpoint of the vector-valued function r(t) = f (t), g(t), h(t) , where f, f' , g, g', h and h' are all continuous for t ∈ [a, b] and where the curve is traversed exactly once as t increases from a to b. The arc length of the space curve is given by: (See the text for the derivation of this result. ) © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 20

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 6 Computing Arc Length in Find the arc length of the curve traced out by the endpoint of the vector-valued function r(t) = 2 t, ln t, t 2 , for 1 ≤ t ≤ e. © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 21

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 6 Computing Arc Length in Solution First, notice that for x(t) = 2 t, y(t) = ln t and z(t) = t 2, we have x'(t) = 2, y'(t) = 1/t and z'(t) = 2 t, and the curve is traversed exactly once for 1 ≤ t ≤ e. © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 22

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 6 Computing Arc Length in Solution © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 23

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 7 Approximating Arc Length in Find the arc length of the curve traced out by the endpoint of the vector-valued function r(t) = e 2 t , sin t, t , for 0 ≤ t ≤ 2. © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 24

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 7 Approximating Arc Length in Solution First, note that for x(t) = e 2 t , y(t) = sin t and z(t) = t, we have x'(t) = 2 e 2 t , y'(t) = cos t and z'(t) = 1, and that the curve is traversed exactly once for 0 ≤ t ≤ 2 Approximate the integral using Simpson’s Rule or the numerical integration routine built into your calculator: s ≈ 53. 8. © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 25

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 8 Finding Parametric Equations for an Intersection of Surfaces Find the arc length of the portion of the curve determined by the intersection of the cone and the plane y + z = 2 in the first octant. © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 26

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 8 Finding Parametric Equations for an Intersection of Surfaces Solution © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 27

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 8 Finding Parametric Equations for an Intersection of Surfaces Solution The portion of the parabola in the first octant must have x ≥ 0 (so t ≥ 0), y ≥ 0 (so t 2 ≤ 4) and z ≥ 0 (always true). This occurs if 0 ≤ t ≤ 2. © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 28

11. 1 VECTOR-VALUED FUNCTIONS EXAMPLE 1. 8 Finding Parametric Equations for an Intersection of Surfaces Solution © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. Slide 29