Vectors Vector A quantity that represents both magnitude

Vectors

Vector: A quantity that represents both magnitude and direction. Give an example of a vector quantity for the following: Displacement: 5 meters East Velocity 50. m/s South Acceleration 4. 7 m/s 2 West

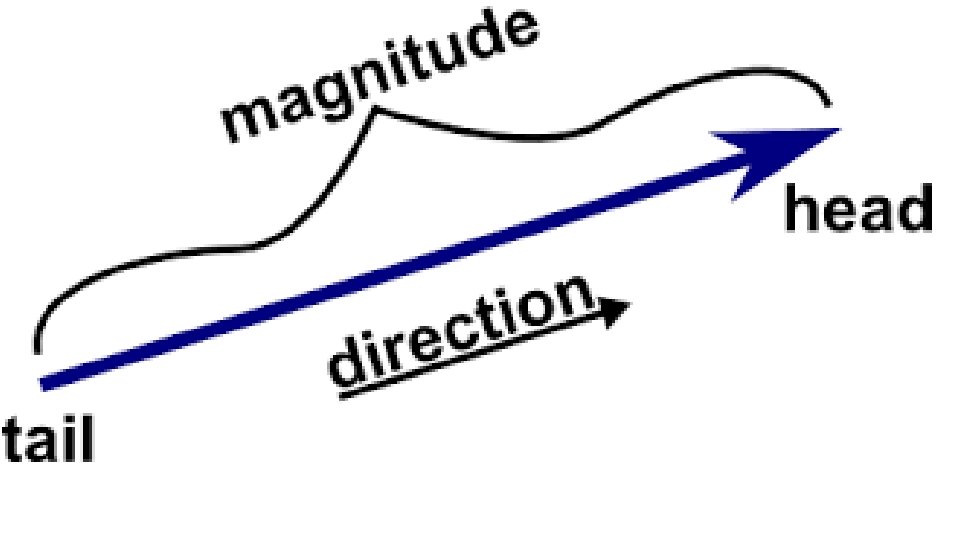
Graphic Representation of a Vector. Elements of a Vector 1. Length represents magnitude 2. Arrow represents direction

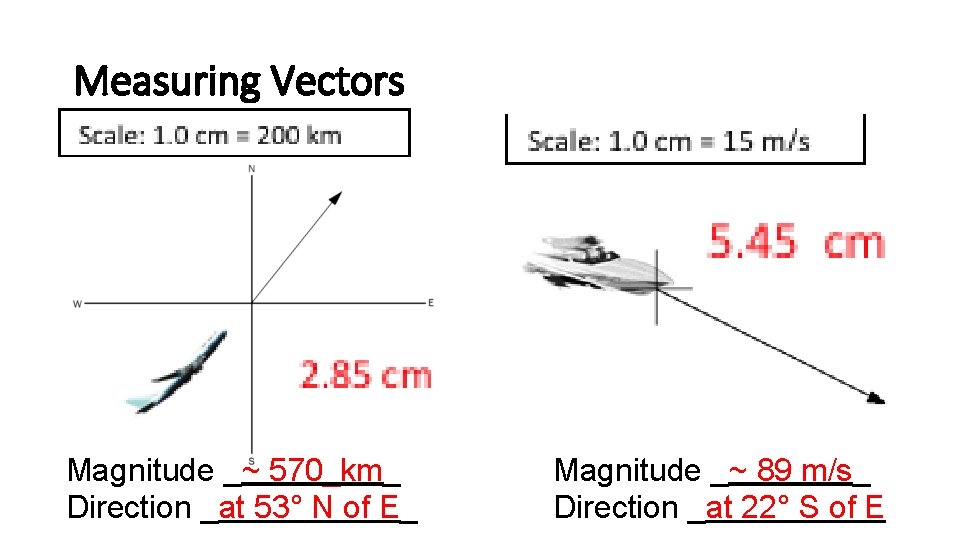
Measuring Vectors Magnitude _~ 570_km_ Direction _at 53° N of E_ Magnitude _~ 89 m/s_ Direction _at 22° S of E

Steps to Drawing a Vector 1. Determine scale. 2. Determine direction or angle. 3. Draw vector with appropriate magnitude (length).

A dog walks east for 20. meters. Scale:

An airplanes flies with a velocity of 2400 km/hr, 15 north of west. Scale

A box is dragged to the right with a force of 30. Newtons at an angle of 20 above the horizon. Scale

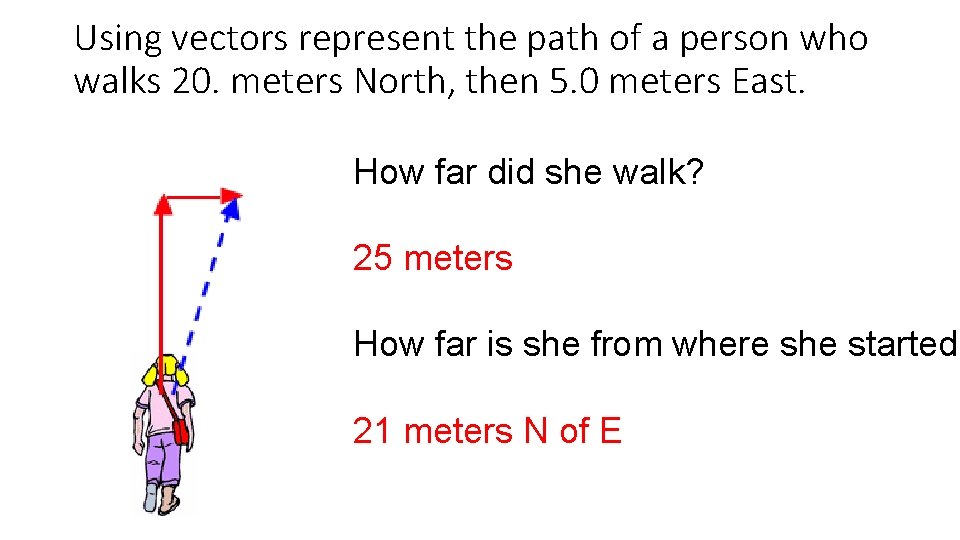
Using vectors represent the path of a person who walks 20. meters North, then 5. 0 meters East. How far did she walk? 25 meters How far is she from where she started? 21 meters N of E

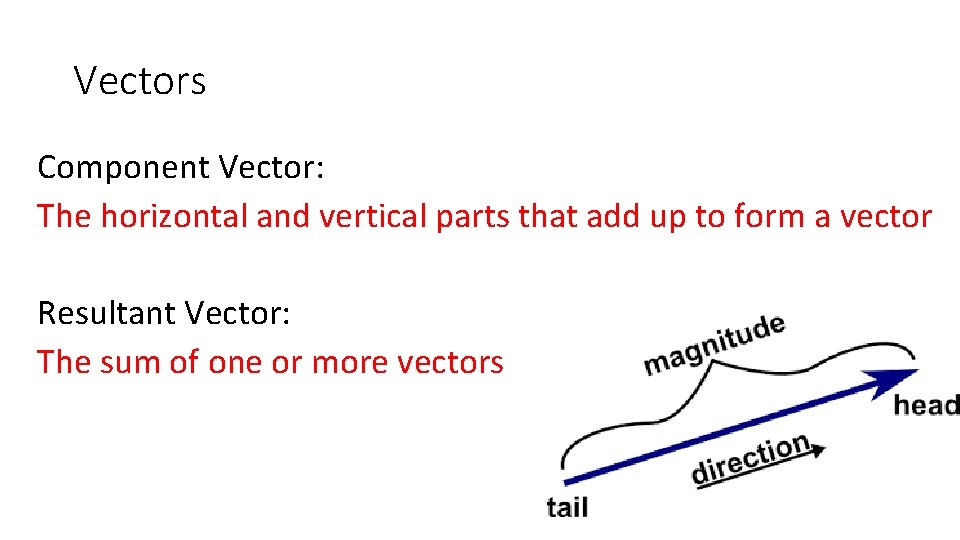
Vectors Component Vector: The horizontal and vertical parts that add up to form a vector Resultant Vector: The sum of one or more vectors

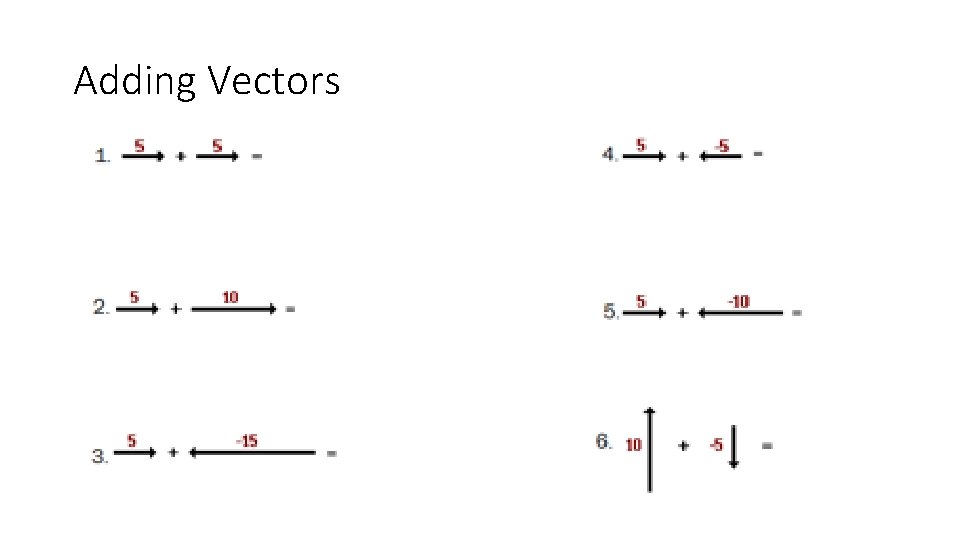
Adding Vectors

A tiger walks from its den 300. meters East, and then walks another 400. meters South. What is the displacement of the tiger from its den? Scale Method Math Method

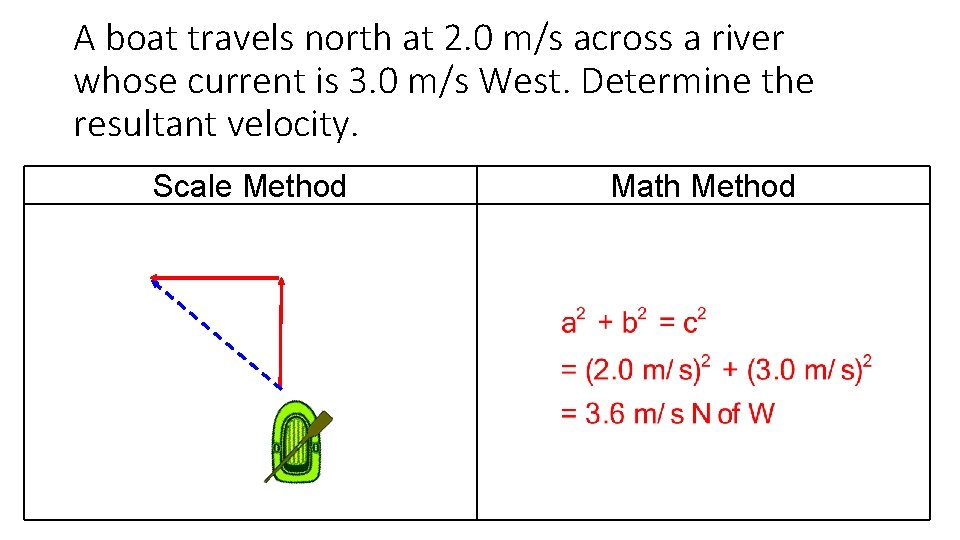
A boat travels north at 2. 0 m/s across a river whose current is 3. 0 m/s West. Determine the resultant velocity. Scale Method Math Method

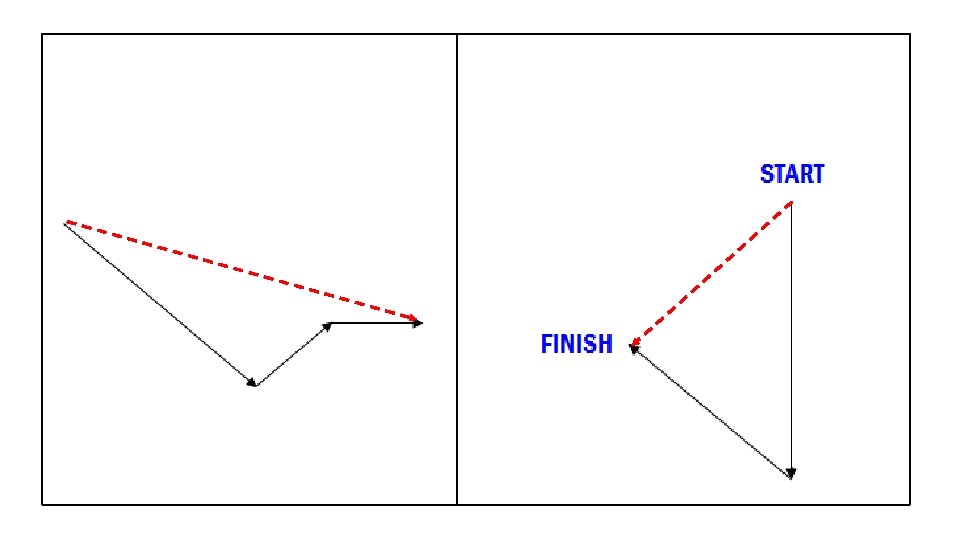
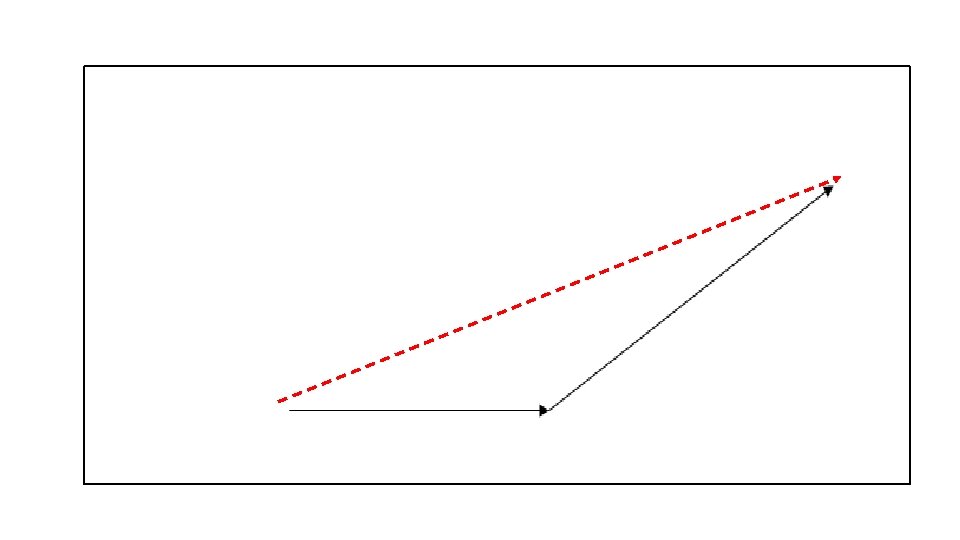
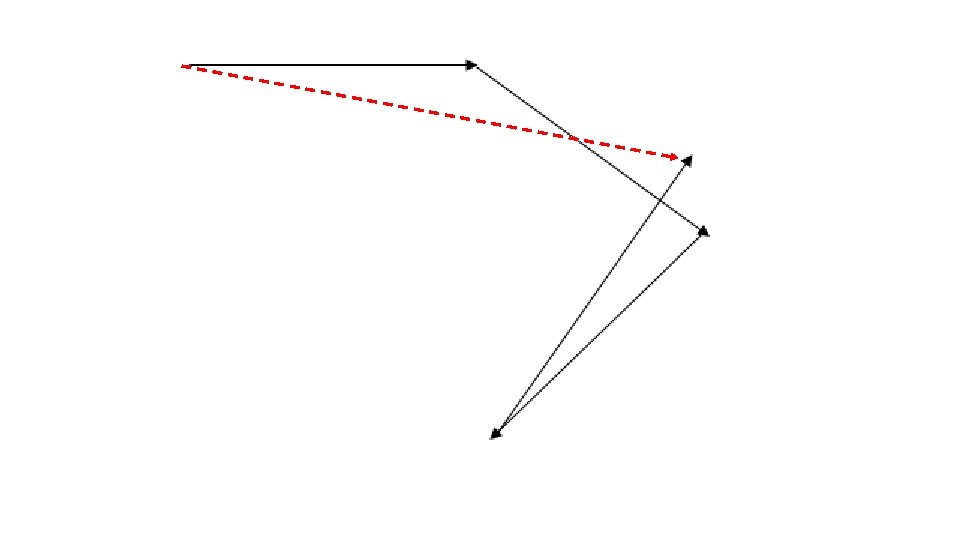
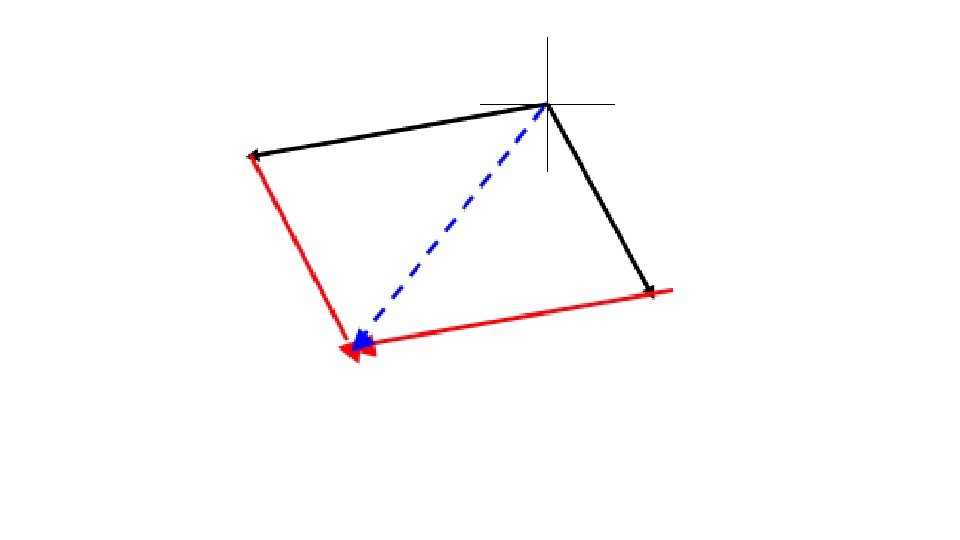
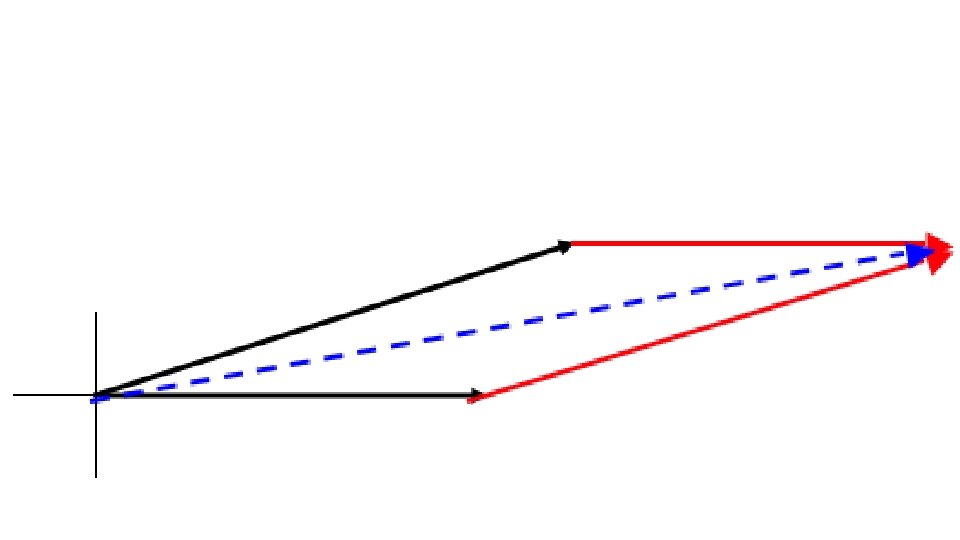
Adding Non-Perpendicular Vectors Draw resultant from ____START____ to ____FINISH____.

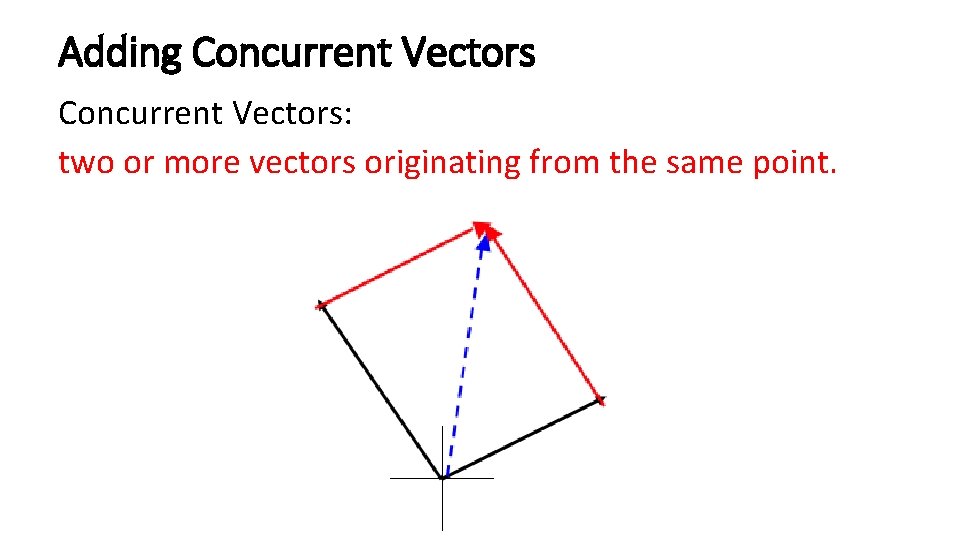
Adding Concurrent Vectors: two or more vectors originating from the same point.

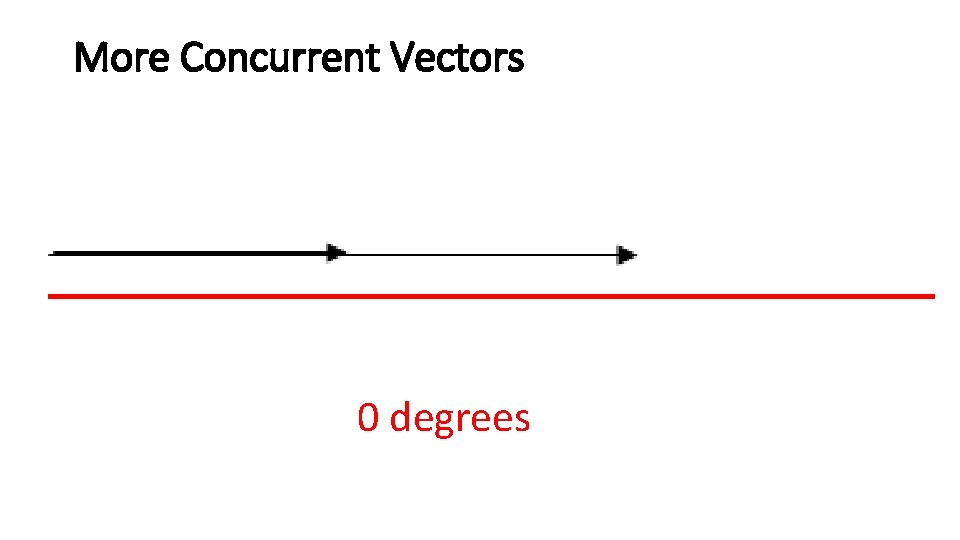
More Concurrent Vectors 0 degrees

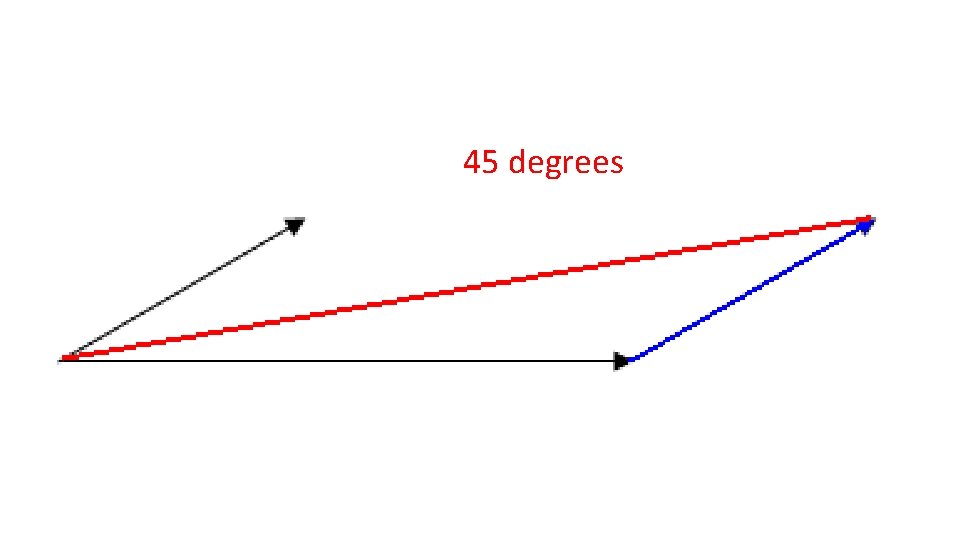
45 degrees

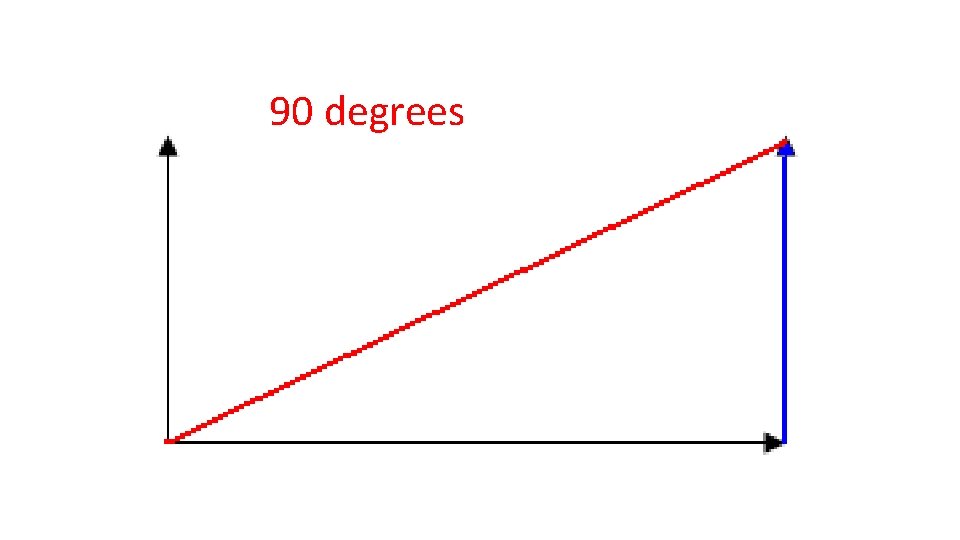
90 degrees

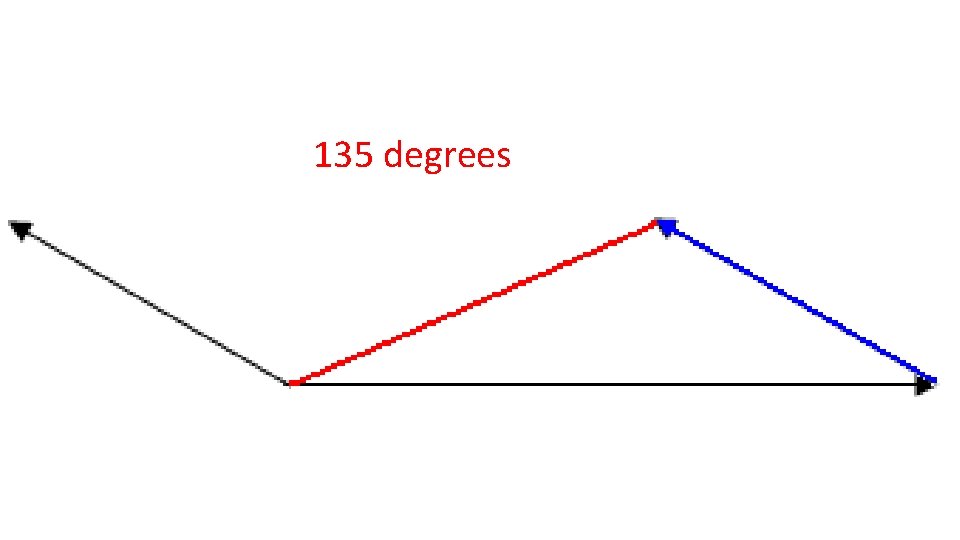
135 degrees

180 degrees

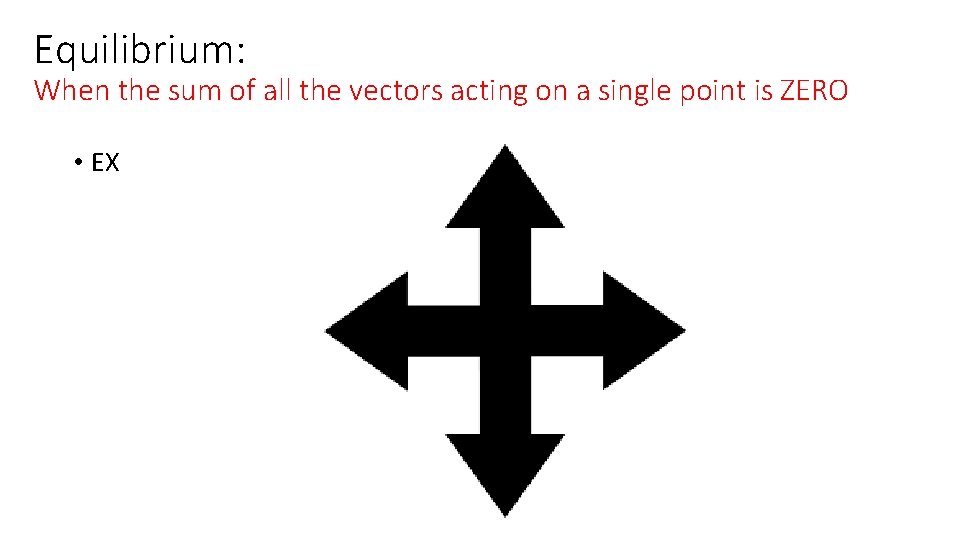
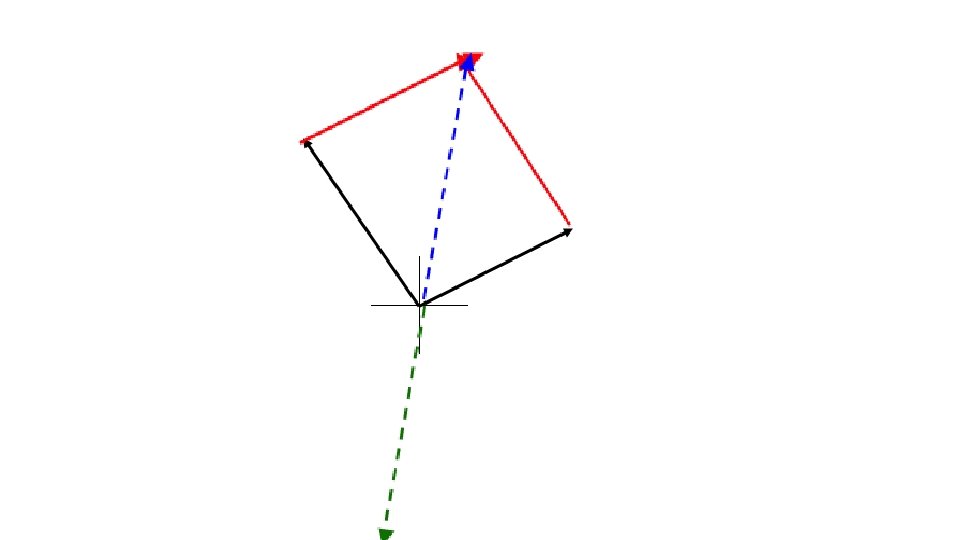
Equilibrium: When the sum of all the vectors acting on a single point is ZERO • EX

Equillibrant: A single vector that is exerted on an object to produce equilibrium, which is the same magnitude as the resultant force but opposite in direction.

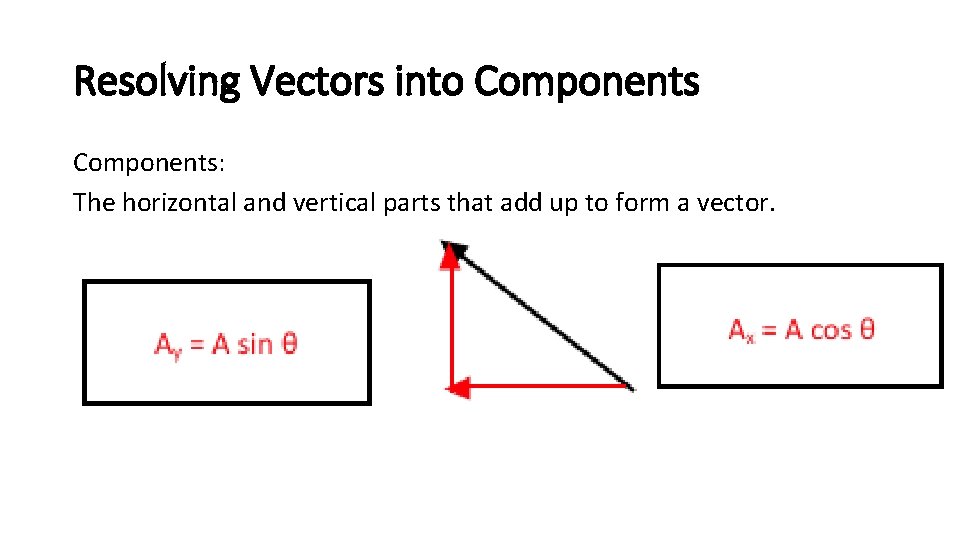
Resolving Vectors into Components: The horizontal and vertical parts that add up to form a vector.

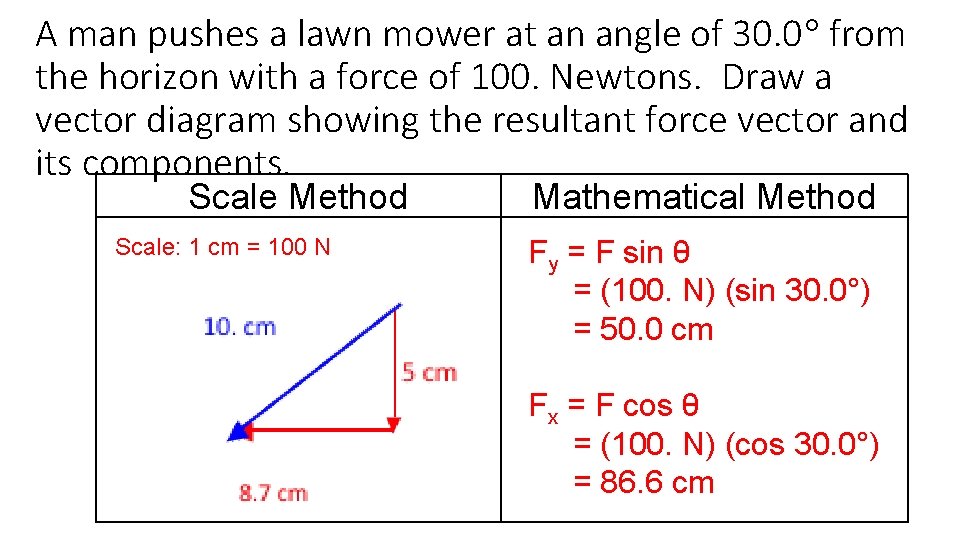
A man pushes a lawn mower at an angle of 30. 0 from the horizon with a force of 100. Newtons. Draw a vector diagram showing the resultant force vector and its components. Scale Method Scale: 1 cm = 100 N Mathematical Method Fy = F sin θ = (100. N) (sin 30. 0°) = 50. 0 cm Fx = F cos θ = (100. N) (cos 30. 0°) = 86. 6 cm

The man pushing the mower begins to push it at a larger angle than in the problem before. What happens to the vertical and horizontal components of the force as the angle increases? As the angle increases, the vertical component increases and the horizontal component decreases.

A horizontal force of 30. Newtons acts on a body concurrently with a 10. Newtons force acting vertically (as shown below). Determine the resultant force.

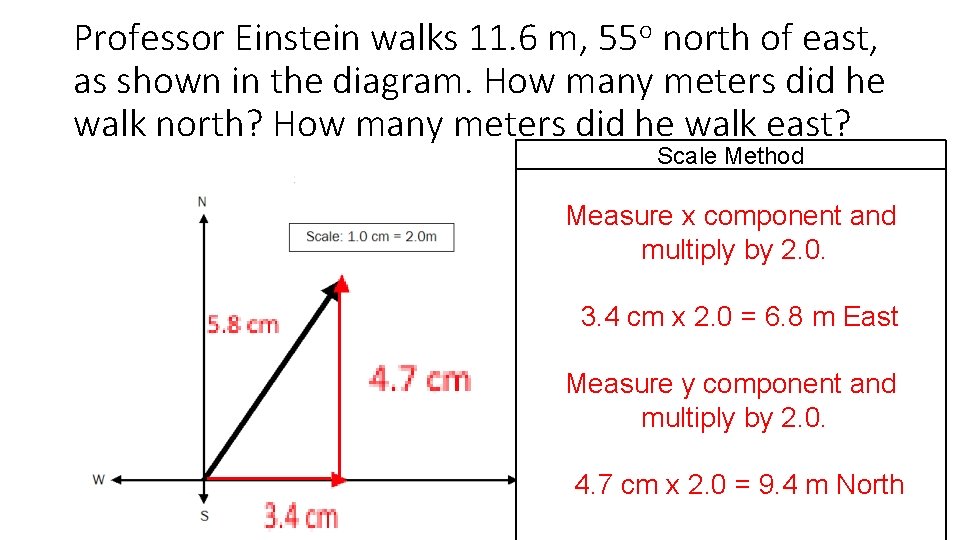
Professor Einstein walks 11. 6 m, 55 o north of east, as shown in the diagram. How many meters did he walk north? How many meters did he walk east? Scale Method Measure x component and multiply by 2. 0. 3. 4 cm x 2. 0 = 6. 8 m East Measure y component and multiply by 2. 0. 4. 7 cm x 2. 0 = 9. 4 m North

Scale Method Measure x component and multiply by 2. 0. Mathematical Method dy = d sin θ = (11. 6 m) (sin 55°) = 9. 5 m North 3. 4 cm x 2. 0 = 6. 8 m East Measure y component and multiply by 2. 0. 4. 7 cm x 2. 0 = 9. 4 m North dx = d cos θ = (11. 6 m) (cos 55°) = 6. 7 m East

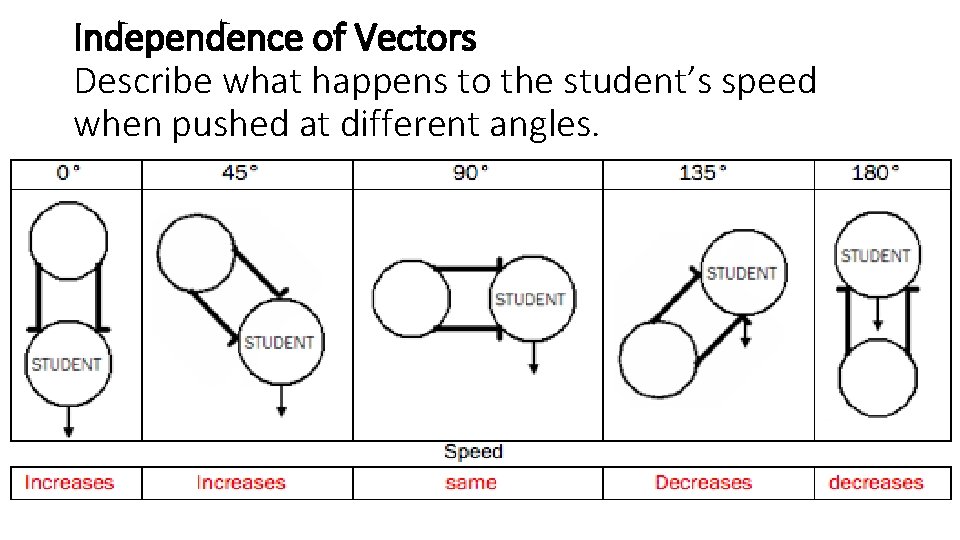
Independence of Vectors Describe what happens to the student’s speed when pushed at different angles.

At which angle was the student’s speed influenced the least? At 90° the student’s speed is least influenced.

A motorboat travels at 8. 5 m/s, north straight across a river that has a current of 3. 8 m/s east.

Construct a statement regarding the independence of vectors. Vectors perpendicular to one another are independent of each other.