Vectors Vector a physical quantity Magnitude Direction Velocity

Vectors • Vector: a physical quantity – Magnitude – Direction – Velocity, force, displacement • Scalar: a physical quantity – Just magnitude – Age, temperature, speed, distance • Neither: not a quantity, a quality – Color, shape

Force • • • Force = a push or pull British Units: pounds SI Units: Newtons 1 N = 1 kg*m/s² Can be measured with a spring scale

Vectors: Diagrams • Vectors = arrows • Length of arrow = magnitude of vector • Direction of arrow = direction of vector • Example: pushing on a shopping cart (depending on how tall you are) you don’t push straight ahead, you push on the handle downward and forward…

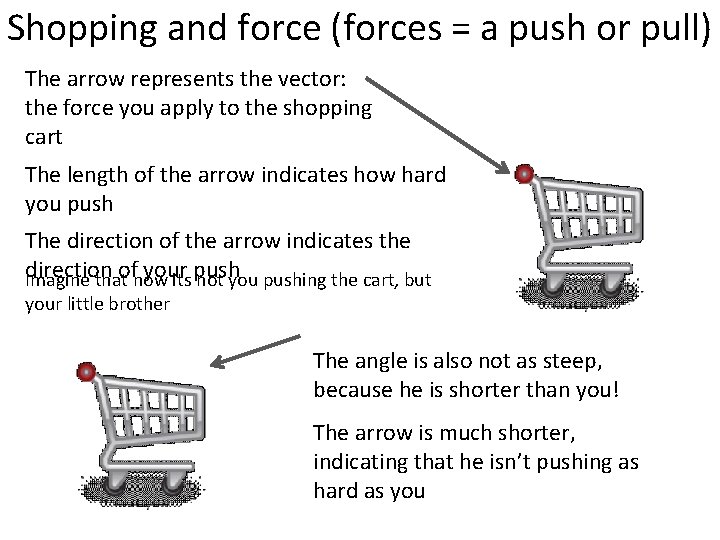
Shopping and force (forces = a push or pull) The arrow represents the vector: the force you apply to the shopping cart The length of the arrow indicates how hard you push The direction of the arrow indicates the direction ofnow your Imagine that its push not you pushing the cart, but your little brother The angle is also not as steep, because he is shorter than you! The arrow is much shorter, indicating that he isn’t pushing as hard as you

Adding Vectors • Whenever 2 (or more!) vectors are combined, the new vector formed is called the resultant • If 2 vectors point in the same direction – Add them • If 2 vectors point in opposite directions – Subtract them – Sign indicates direction • If 2 vectors point in any other directions – Parallelogram rule

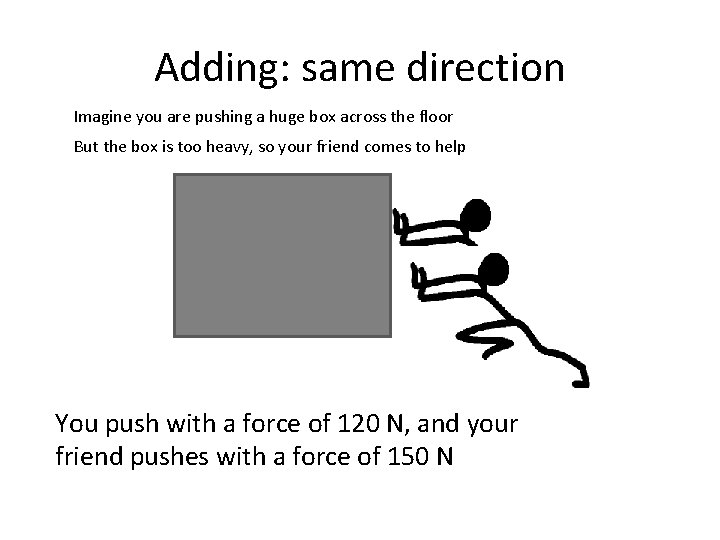
Adding: same direction Imagine you are pushing a huge box across the floor But the box is too heavy, so your friend comes to help You push with a force of 120 N, and your friend pushes with a force of 150 N

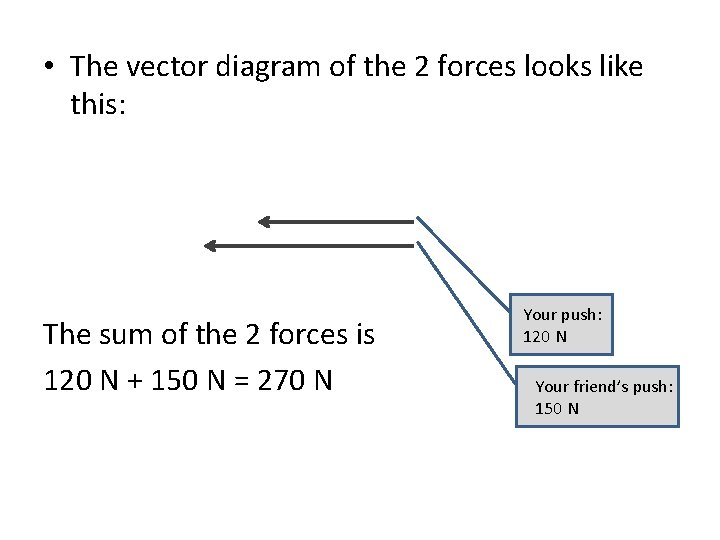
• The vector diagram of the 2 forces looks like this: The sum of the 2 forces is 120 N + 150 N = 270 N Your push: 120 N Your friend’s push: 150 N

Practice with displacement • Displacement is a vector! – The vector from where you start to where you end • Displacement 1: walk 20 yards north • Displacement 2: walk 5 yards north • What is the resultant displacement? • 25 yards north!

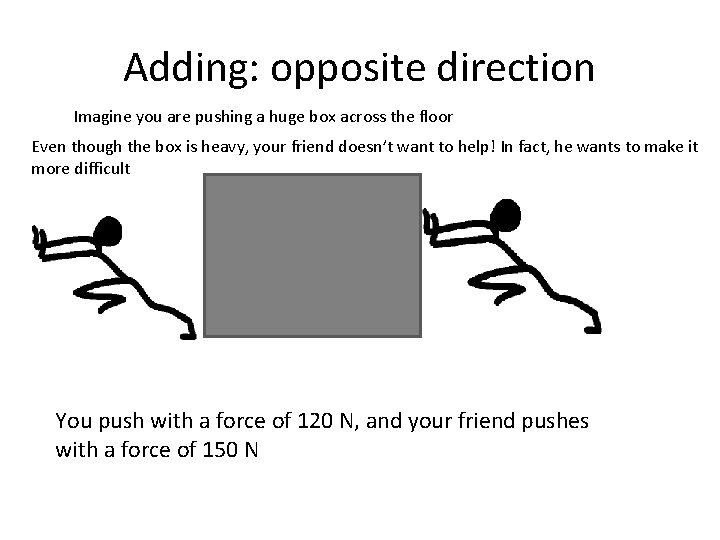
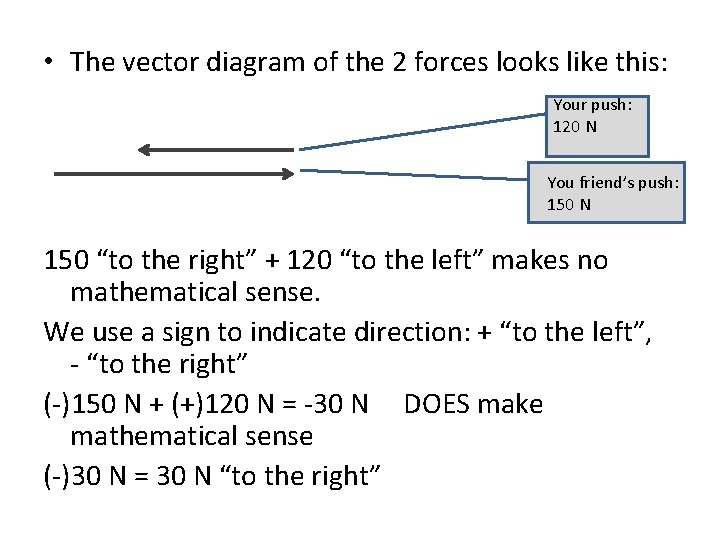
Adding: opposite direction Imagine you are pushing a huge box across the floor Even though the box is heavy, your friend doesn’t want to help! In fact, he wants to make it more difficult You push with a force of 120 N, and your friend pushes with a force of 150 N

• The vector diagram of the 2 forces looks like this: Your push: 120 N You friend’s push: 150 N 150 “to the right” + 120 “to the left” makes no mathematical sense. We use a sign to indicate direction: + “to the left”, - “to the right” (-)150 N + (+)120 N = -30 N DOES make mathematical sense (-)30 N = 30 N “to the right”

Practice with displacement • Displacement is a vector! – The vector from where you start to where you end • Displacement 1: walk 20 yards north • Displacement 2: walk 5 yards south • what is the resultant displacement? • 15 yards north!

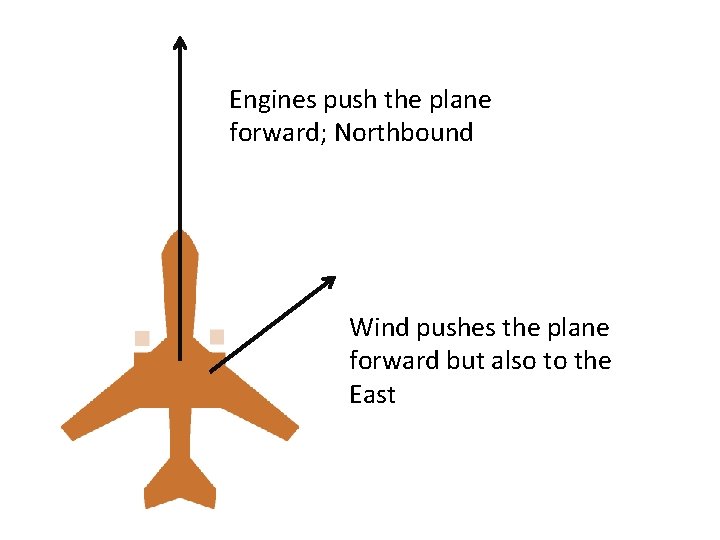
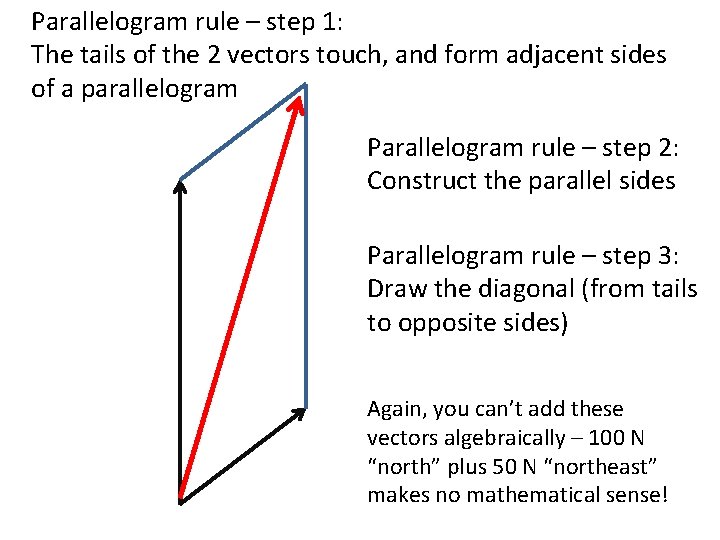
Parallelogram Rule • Tails of the 2 vectors touch • The 2 vectors form adjacent sides of a parallelogram • The diagonal (from tails to tip) is the resultant • Example: You are in an airplane flying northbound, but the wind is blowing northeast

Engines push the plane forward; Northbound Wind pushes the plane forward but also to the East

Parallelogram rule – step 1: The tails of the 2 vectors touch, and form adjacent sides of a parallelogram Parallelogram rule – step 2: Construct the parallel sides Parallelogram rule – step 3: Draw the diagonal (from tails to opposite sides) Again, you can’t add these vectors algebraically – 100 N “north” plus 50 N “northeast” makes no mathematical sense!

Practice with displacement • Displacement 1 = 20 yards north • Displacement 2 = 5 yards northwest • What is the resultant displacement? Resultant! Draw/construct parallel sides 20 yds N The 2 vectors to be combined are drawn tail-totail 5 yds NW

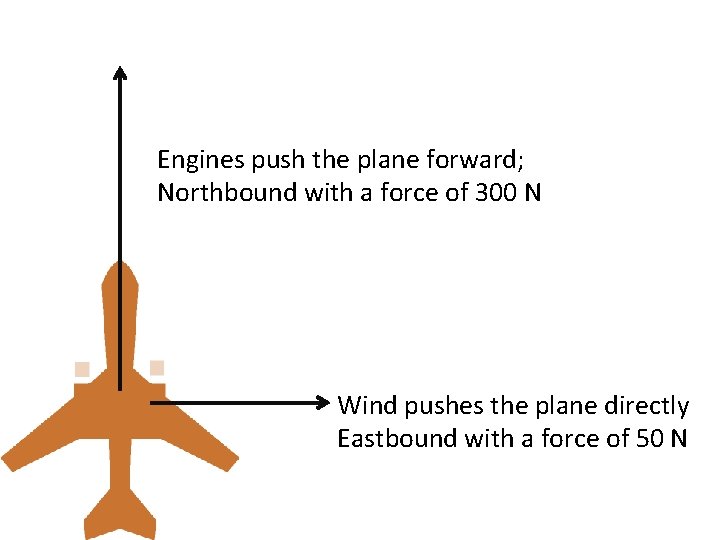
Parallelogram Rule: Special Case • If the 2 vectors are at 90° to each other • The parallelogram they form is a rectangle (or square) • The diagonal can be found numerically using the Pythagorean theorem • Example: you are in a plane flying northbound and the wind is directly east

Engines push the plane forward; Northbound with a force of 300 N Wind pushes the plane directly Eastbound with a force of 50 N

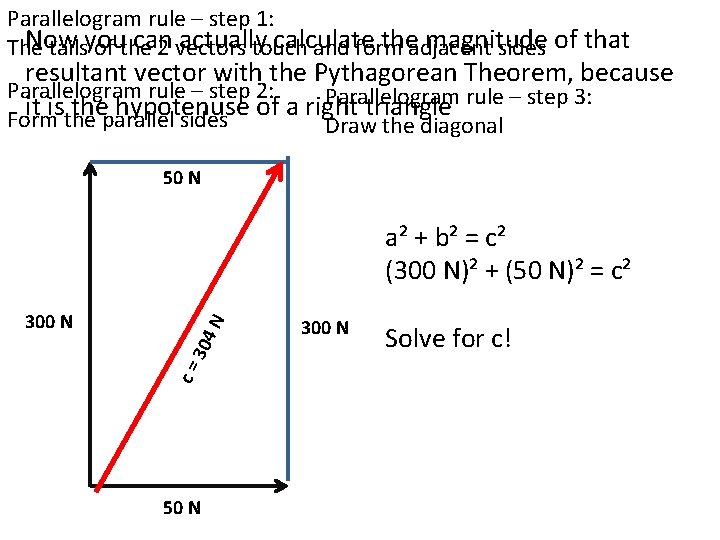
Parallelogram rule – step 1: Now can actually calculate theadjacent magnitude The tailsyou of the 2 vectors touch and form sides of that resultant vector with the Pythagorean Theorem, because Parallelogram rule – step 2: Parallelogram rule – step 3: it is the hypotenuse of a right triangle Form the parallel sides Draw the diagonal 50 N 304 c= 300 N N a² + b² = c² (300 N)² + (50 N)² = c² 50 N 300 N Solve for c!

Practice with displacement • Displacement 1 = 20 yards north • Displacement 2 = 5 yards west • What is the resultant displacement? Finally, use the Pythagorean Theorem to find the length of the hypotenuse (resultant)! First, diagram the vectors, apply the parallelogram rule 20 yds N Next, identify the right triangle 5 yds W

Balanced and Unbalanced Forces • Balanced Forces: – Tug of war, stalemate – Driving at constant speed on the freeway Frictionon People pull the carleft pull to the left backward All are in Equilibrium: no net force Engine torque People(via on the right on axle) pushes pull to the rightcar forward

Unbalanced Forces: • Accelerating onto the freeway Air resistance • Sky diving (friction) pushes up Engine pushes car forward Friction pulls car backward Weight (the pull of gravity) pulls down Object speeds up or slows down in the direction of net force (the details of this = Newton’s 2 nd Law)

Newton’s 1 st Law • All objects remain at rest OR continue in a straight line path at constant speed UNLESS acted on by a net force • The law of inertia • “inertia” = an object’s tendency to keep doing what it was already doing

Lab Activity: Treasure Hunt • Groups of less than 6 students each • All groups begin at the same starting point: Middle of plaza • Groups create a “treasure map, ” but with notecards: each card gives a single displacement • 10 displacement vector • directions – Must range from small (2 ft) to large (20 ft) • – Must not go in parking lot – Must include all 4 directions • (N, S, E, W) – No intermediate directions (NW, SE, etc) – Use lines on plaza patio for direction reference – Do not number direction cards (they will be mixed up) – Color code cards and “treasure marker” (“X” on a white paper) Your direction cards will be shuffled and given to another team Team who finds the “X” of another team wins the “treasure chest” BEFORE YOU GO discuss: what effect will shuffling the cards have on the success of the treasure hunt?

HOMEWORK/classwork? ? ? 8 th edition • Pg 52 – Review q 6 -8 • pg 53 – Exercises 3 -4 • Pg 55 – Problems 1 -2 10 th edition • Pg 87 – “one step calculations” 1, 2, 4 • Pg. 89 – Exercises 31 -32 • Pg. 90 – Problems 5 -6