Vectors OCR Stage 10 A VECTOR Describes the

Vectors OCR Stage 10

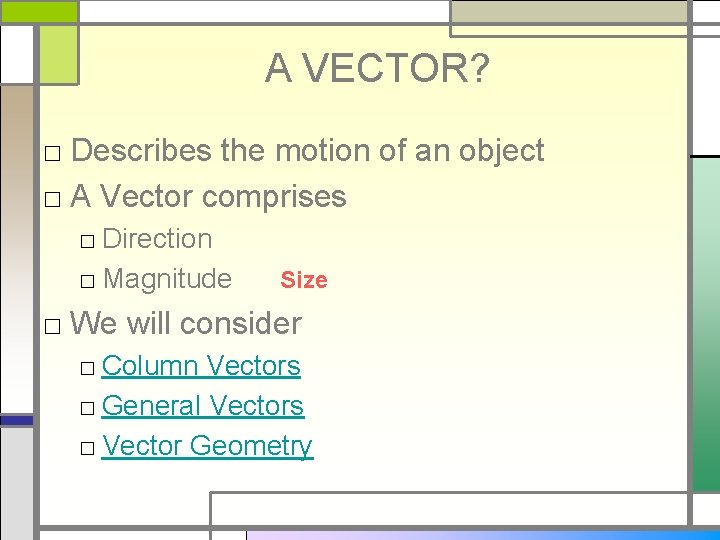
A VECTOR? □ Describes the motion of an object □ A Vector comprises □ Direction □ Magnitude Size □ We will consider □ Column Vectors □ General Vectors □ Vector Geometry

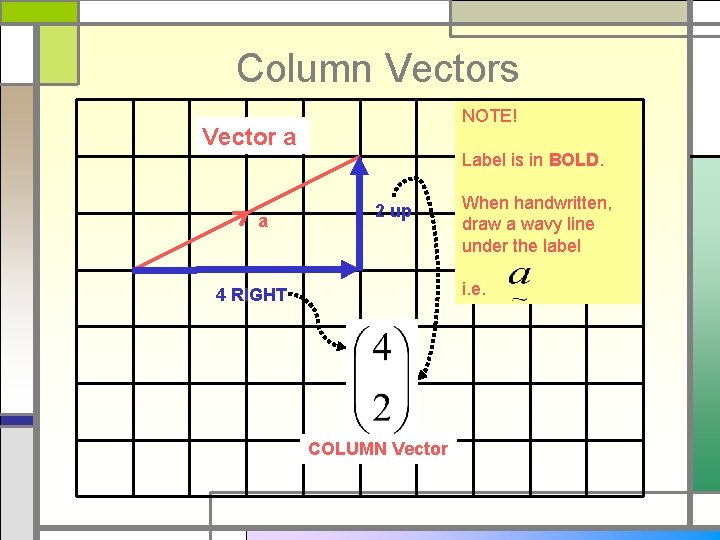
Column Vectors NOTE! Vector a a Label is in BOLD. 2 up When handwritten, draw a wavy line under the label i. e. 4 RIGHT COLUMN Vector

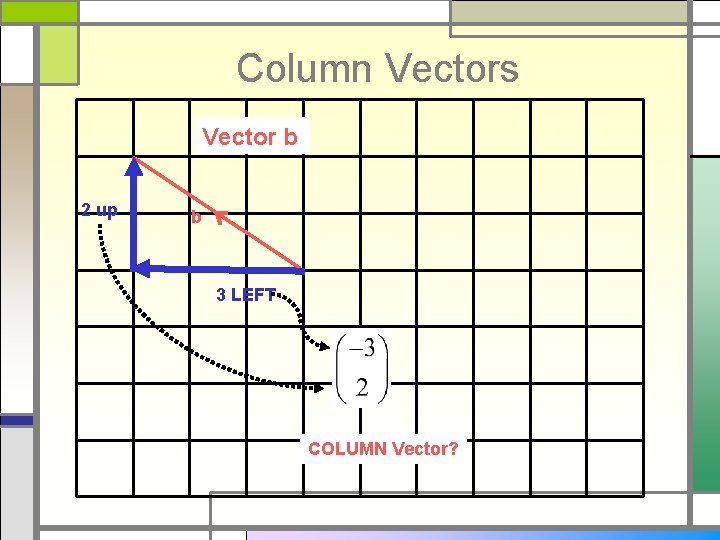
Column Vectors Vector b 2 up b 3 LEFT COLUMN Vector?

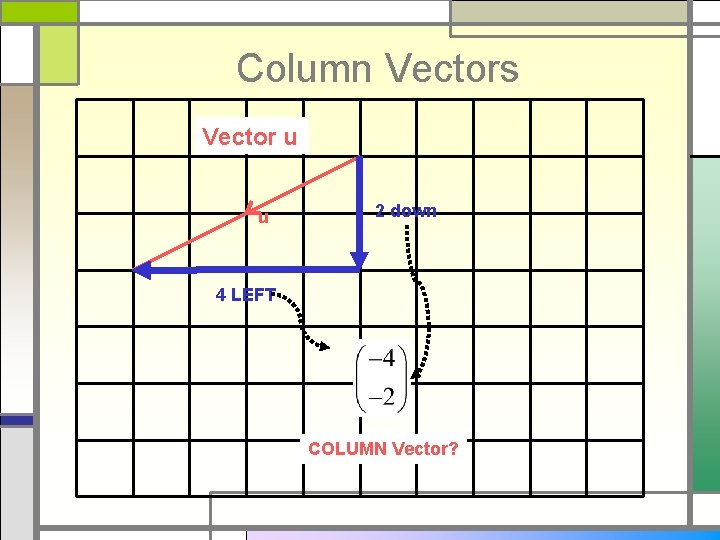
Column Vectors Vector u 2 down n 4 LEFT COLUMN Vector?

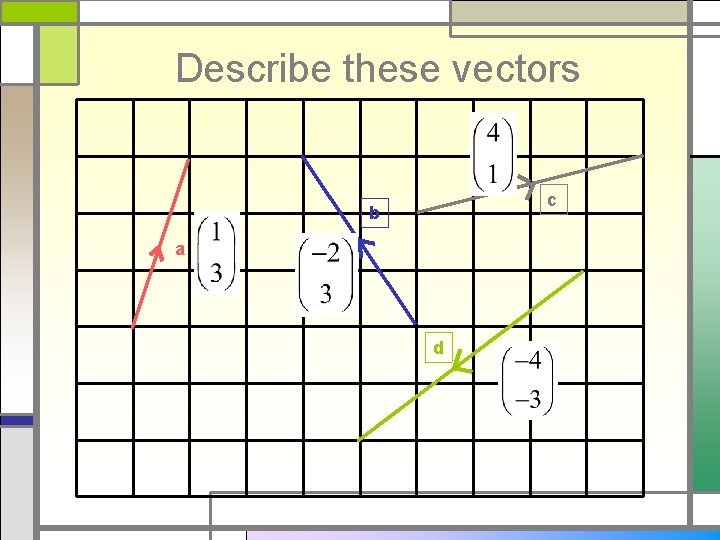
Describe these vectors c b a d

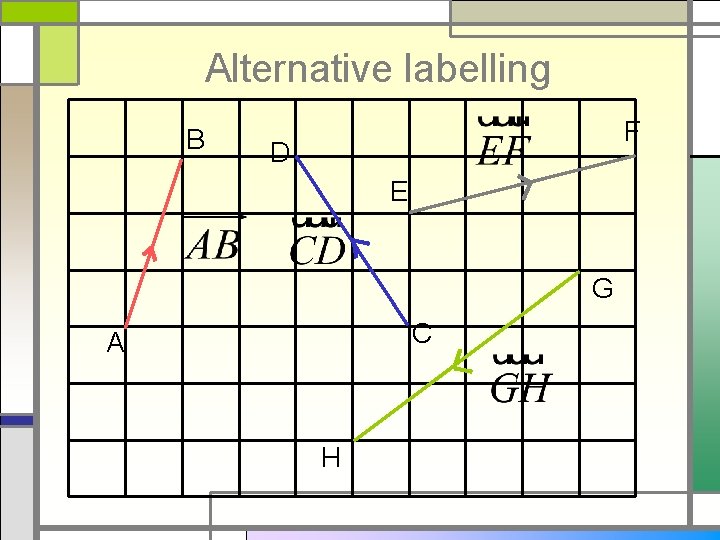
Alternative labelling B F D E G C A H

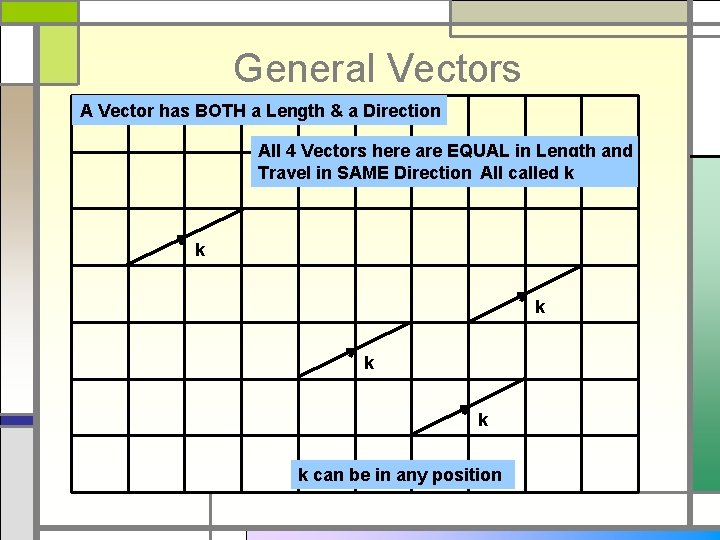
General Vectors A Vector has BOTH a Length & a Direction All 4 Vectors here are EQUAL in Length and Travel in SAME Direction. All called k k k can be in any position

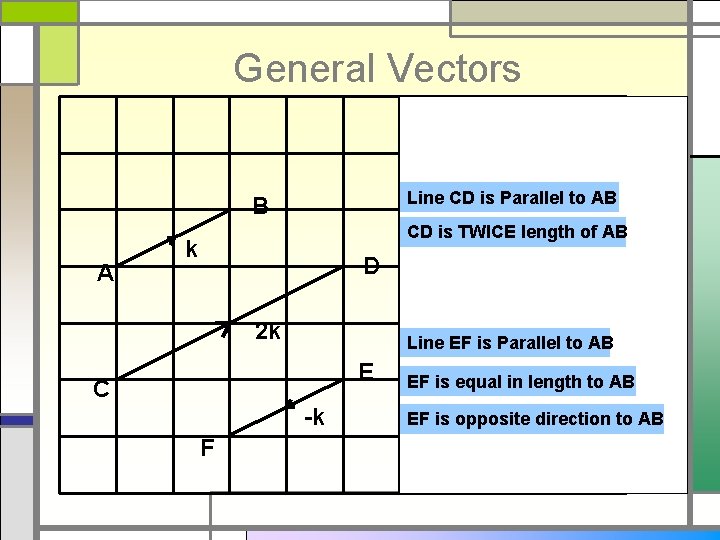
General Vectors Line CD is Parallel to AB B A CD is TWICE length of AB k D 2 k Line EF is Parallel to AB E C -k F EF is equal in length to AB EF is opposite direction to AB

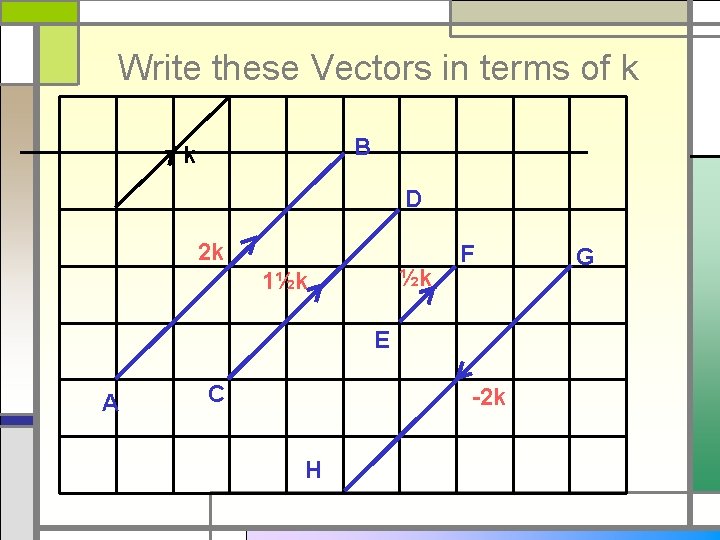
Write these Vectors in terms of k B k D 2 k ½k 1½k F E A C -2 k H G

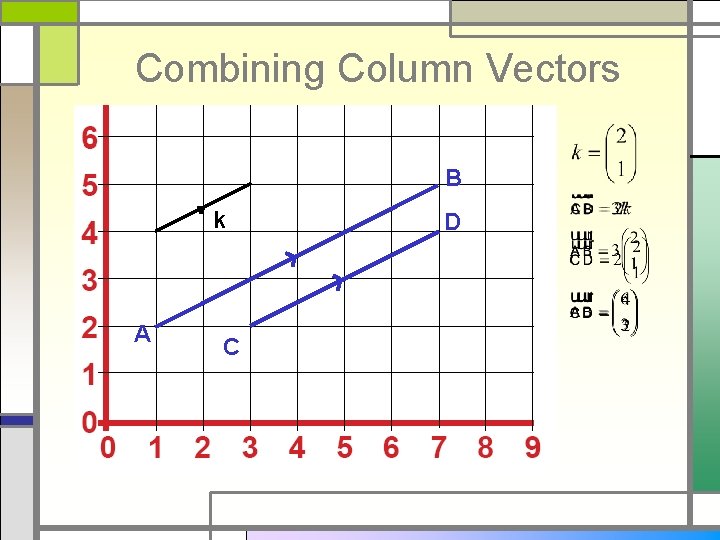
Combining Column Vectors B k A C D

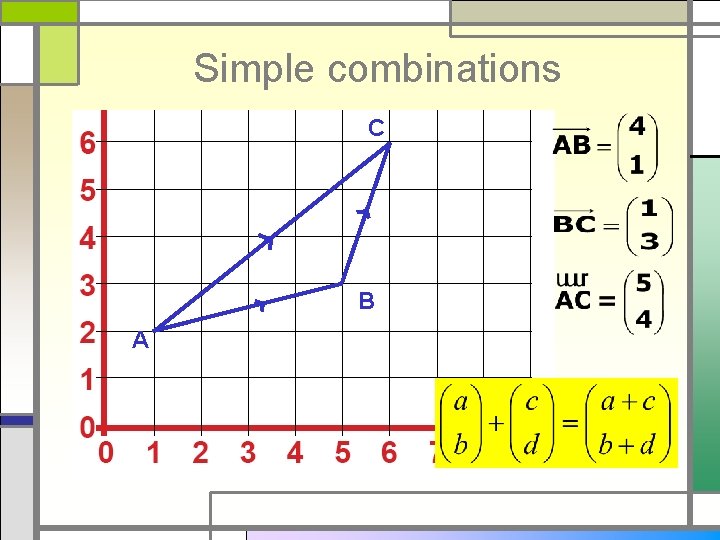
Simple combinations C B A

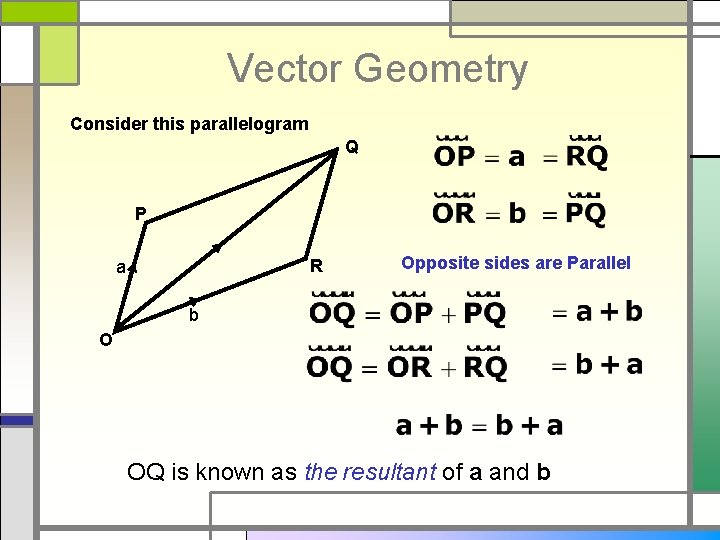
Vector Geometry Consider this parallelogram Q P R a Opposite sides are Parallel b O OQ is known as the resultant of a and b

Resultant of Two Vectors □ Is the same, no matter which route is followed □ Use this to find vectors in geometrical figures

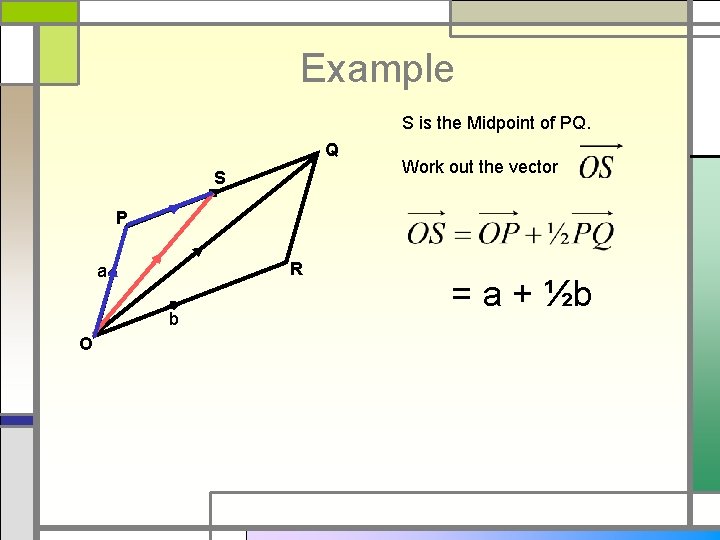
Example S is the Midpoint of PQ. Q . S P R a b O Work out the vector = a + ½b

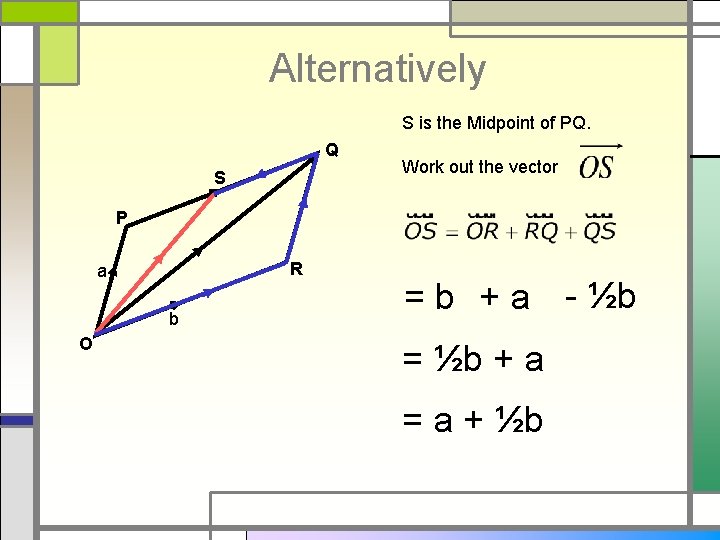
Alternatively S is the Midpoint of PQ. Q . S P R a b O Work out the vector = b + a - ½b = ½b + a = a + ½b

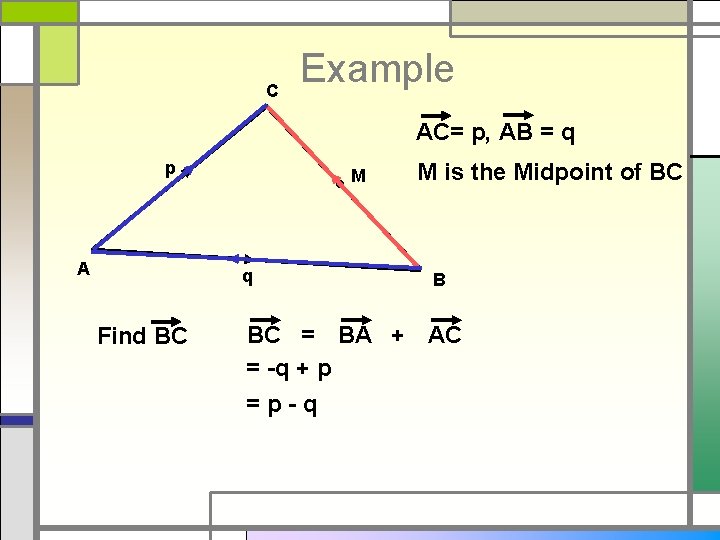
C Example AC= p, AB = q p A M q Find BC M is the Midpoint of BC B BC = BA + AC = -q + p =p-q

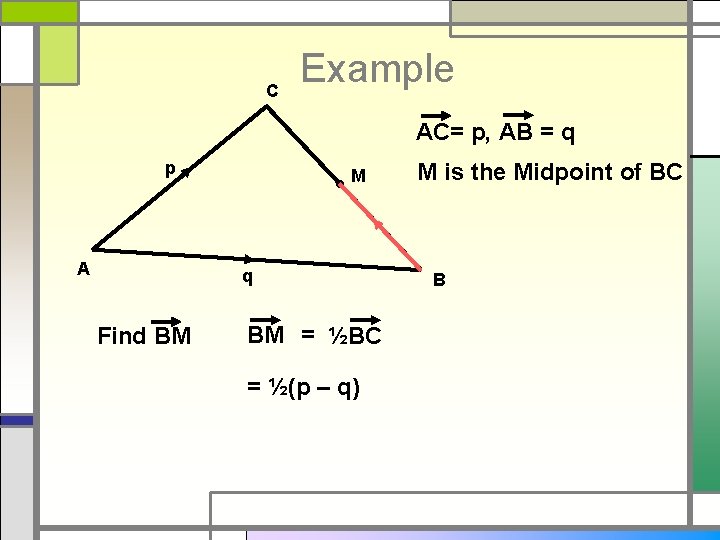
C Example AC= p, AB = q p A M q Find BM BM = ½BC = ½(p – q) M is the Midpoint of BC B

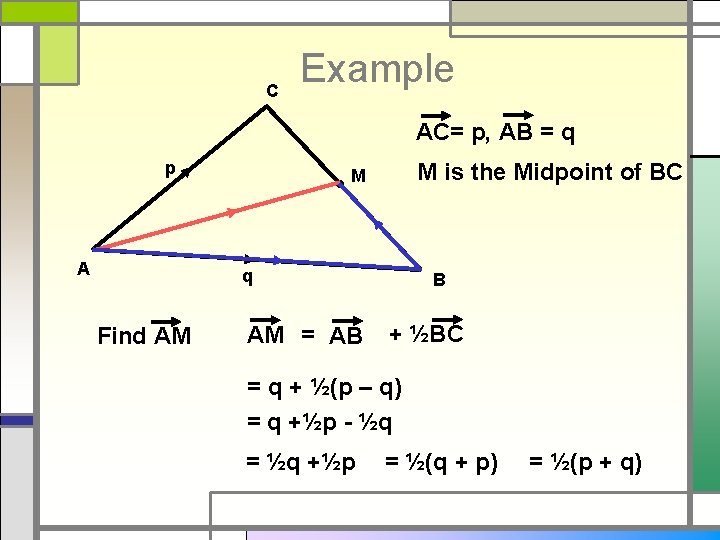
C Example AC= p, AB = q p A M is the Midpoint of BC M q Find AM AM = AB B + ½BC = q + ½(p – q) = q +½p - ½q = ½q +½p = ½(q + p) = ½(p + q)

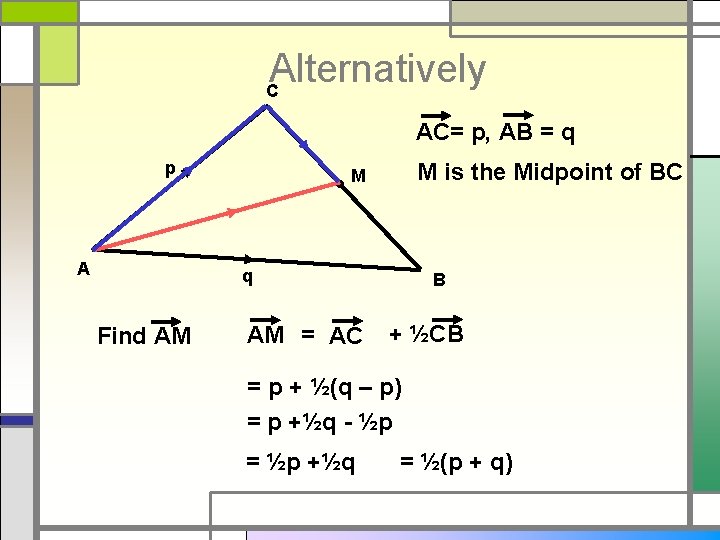
Alternatively C AC= p, AB = q p A M is the Midpoint of BC M q Find AM AM = AC B + ½CB = p + ½(q – p) = p +½q - ½p = ½p +½q = ½(p + q)