Vectors Magnitude Direction Form Vectors are quantities that

Vectors Magnitude - Direction Form Vectors are quantities that have both magnitude (size) and direction. (5, 30˚) We will now be looking at a new way of describing vectors, called Magnitude-Direction Form, or Polar Form. The general form of a vector written in this way is (r, θ), where r is its magnitude and θ is the angle the vector makes with the positive x-axis (positive i direction) 5 30˚ +

Vectors Magnitude - Direction Form Example: Write the vector a = 4 i +2 j in magnitude - direction form. The magnitude of a is given by the length of the vector arrow. a θ 2 4 Using Pythagoras’ Theorem, a = The direction is given by the angle θ = 0. 5 θ = tan -1 (0. 5) = 26. 6˚ to 3 s. f. So the vector a = (4. 47, 26. 6˚) = 4. 47 to 3 s. f.

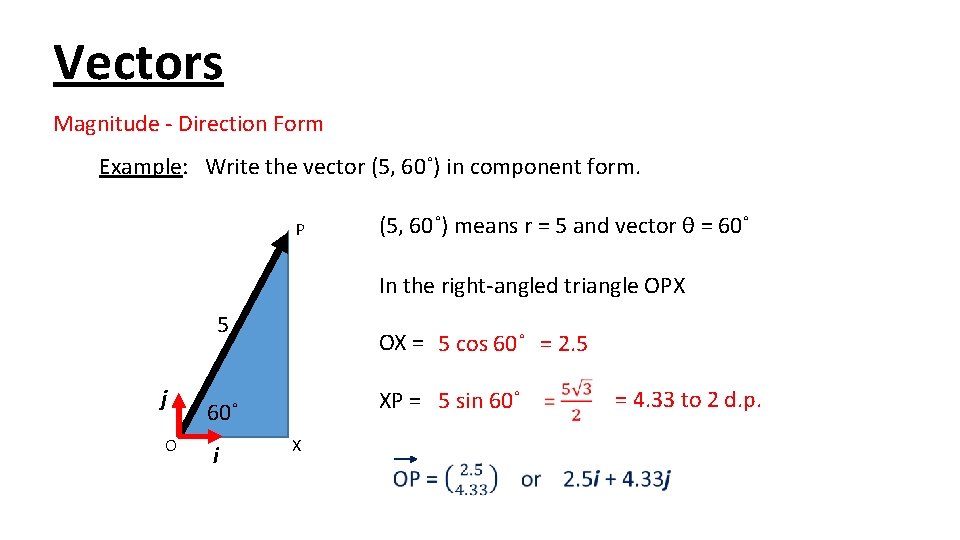
Vectors Magnitude - Direction Form Example: Write the vector (5, 60˚) in component form. P (5, 60˚) means r = 5 and vector θ = 60˚ In the right-angled triangle OPX 5 j O OX = 5 cos 60˚ = 2. 5 XP = 5 sin 60˚ i X = 4. 33 to 2 d. p.

Vectors Magnitude - Direction Form Example: Write the vector (5, 300˚) in component form. 300˚ O (5, 300˚) means r = 5 and vector θ = 300˚ 60˚ In the right-angled triangle OPY 5 Y 60˚ YP = 5 cos 60˚ = 2. 5 OY = 5 sin 60˚ P = 4. 33 to 2 d. p. Notice the j component is negative.

Vectors Unit Vectors A Unit Vector is a vector with a magnitude of 1, like i or j. To find a unit vector in the same direction as a given vector, divide that vector by its magnitude. So the vector a = 3 i + 5 j has magnitude 3 i + 5 j a Note the

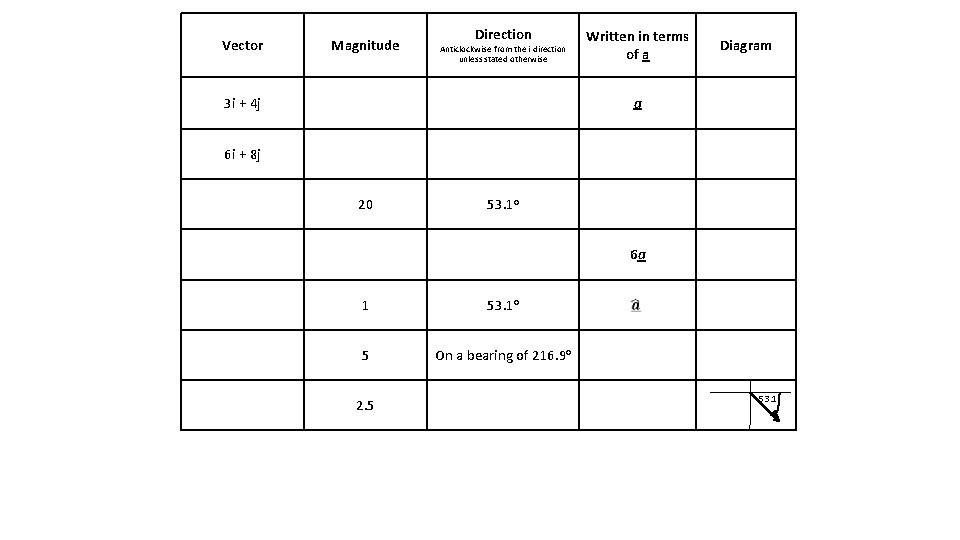
Vector Magnitude Direction Anticlockwise from the i direction unless stated otherwise 3 i + 4 j Written in terms of a Diagram a 6 i + 8 j 20 53. 1 o 6 a 1 53. 1 o 5 On a bearing of 216. 9 o 2. 5 53. 1

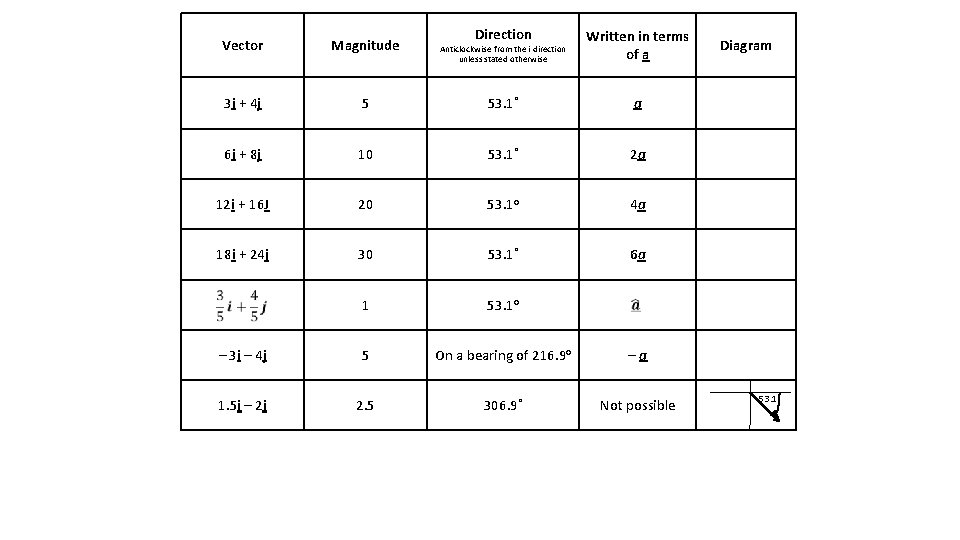
Anticlockwise from the i direction unless stated otherwise Direction Written in terms of a 5 53. 1˚ a 6 i + 8 j 10 53. 1˚ 2 a 12 i + 16 J 20 53. 1 o 4 a 18 i + 24 j 30 53. 1˚ 6 a 1 53. 1 o – 3 i – 4 j 5 On a bearing of 216. 9 o –a 1. 5 i – 2 j 2. 5 306. 9˚ Not possible Vector Magnitude 3 i + 4 j Diagram 53. 1

Convert the following vectors into Magnitude-Direction form: a) 5 i + 6 j b) 4 i + j c) 3 i – 7 j d) – 2 i + 4 j e) – 6 i – 4 j Convert the following vectors into Component form: a) (10, 30˚) b) (5, 245˚) c) (6, 121˚) d) (5, – 80˚) e) (9, 197˚) For each set of questions, it will help to sketch them on a set of axes to decide which angle you need to be referring to.

Convert the following vectors into Magnitude-Direction form: a) 5 i + 6 j = ( 7. 81 , 50. 19˚ ) b) 4 i + j = ( 4. 12 , 14. 04˚ ) c) 3 i – 7 j = ( 7. 62 , – 66. 80˚ ) d) – 2 i + 4 j = ( 4. 47 , 116. 57˚ ) e) – 6 i – 4 j = ( 7. 21 , – 146. 31˚ ) Convert the following vectors into Component form: a) (10, 30˚) = 8. 66 i + 5 j b) (5, 245˚) = 2. 11 i – 4. 53 j c) (6, 121˚) = – 3. 09 i + 5. 14 j d) (5, – 80˚) = 0. 87 i – 4. 92 j e) (9, 197˚) = – 8. 61 i – 2. 63 j For each set of questions, it will help to sketch them on a set of axes to decide which angle you need to be referring to.