VECTORS Do you remember the difference between a

VECTORS

Do you remember the difference between a scalar and a vector? Scalars are quantities which are fully described by a magnitude alone. Vectors are quantities which are fully described by both a magnitude and a direction.

Intro to Vectors Warm-up A bear walks one mile south, then one mile west, and finally walks one mile north. After his brisk walk, the bear ends back where he started. What color is the bear? ? ?

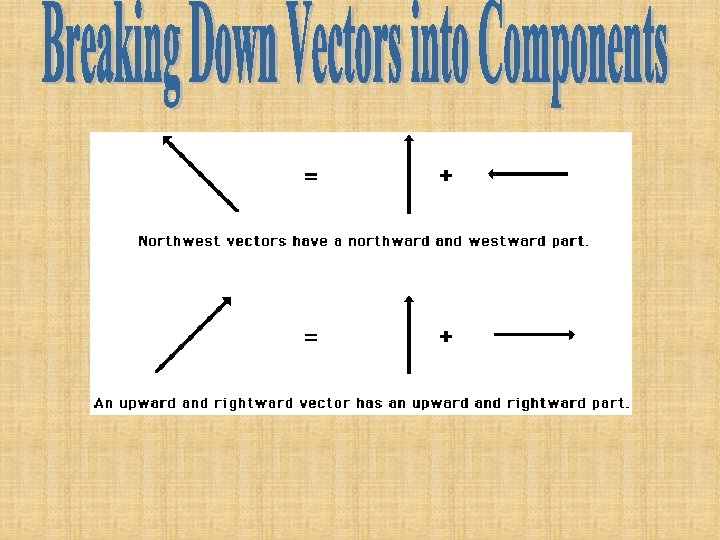
1. The length of the line represents the magnitude and the arrow indicates the direction. 2. The magnitude and direction of the vector is clearly labeled.

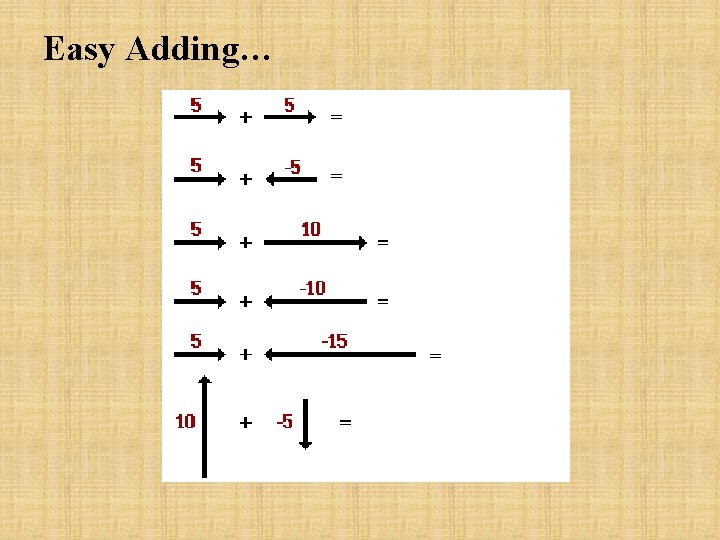
Easy Adding…

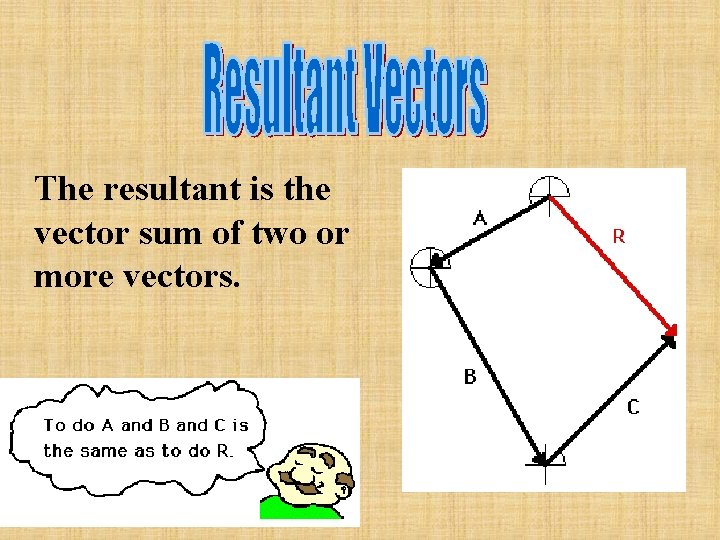
The resultant is the vector sum of two or more vectors.

1. Select an appropriate scale (e. g. , 1 cm = 5 km) 2. Draw and label 1 st vector to scale. *The tail of each consecutive vector begins at the head of the most recent vector* 3. Draw and label 2 nd vector to scale starting at the head of the 1 st vector. 4. Draw the resultant vector (the summative result of the addition of the given vectors) by connecting the tail of the 1 st vector to the head of the 2 nd vector. (initial to final pt. ) 5. Determine the magnitude and direction of the resultant vector by using a protractor, ruler, and the indicated scale; then label the resultant vector.

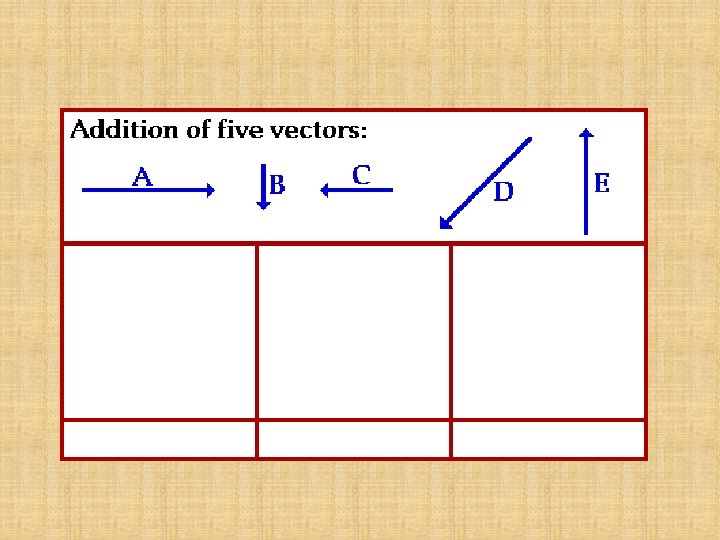
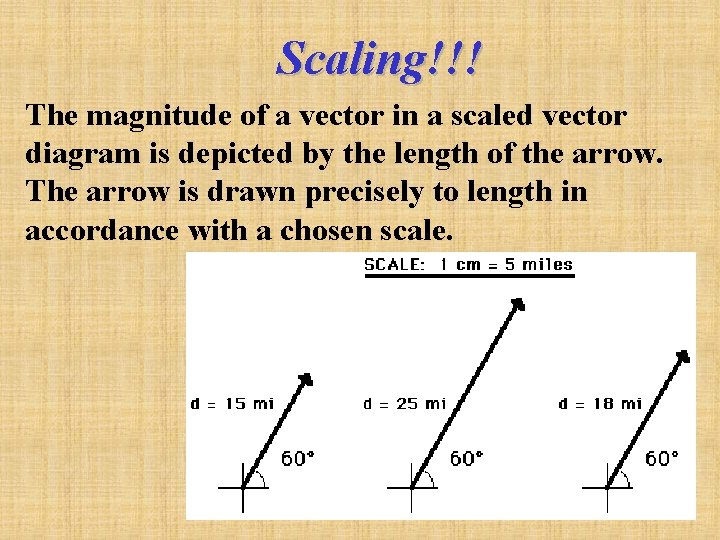
Scaling!!! The magnitude of a vector in a scaled vector diagram is depicted by the length of the arrow. The arrow is drawn precisely to length in accordance with a chosen scale.

Compass Coordinate System Use the same scale for all vector magnitudes • • Δx = 30 m @ 20º E of N V = 20 m/s @ 30º W of N a = 10 m/s 2@ 40º W of S F = 50 N @ 10º S of E W N E To Draw direction: Ex. 20º E of N: Start w/ North and go 20° East S

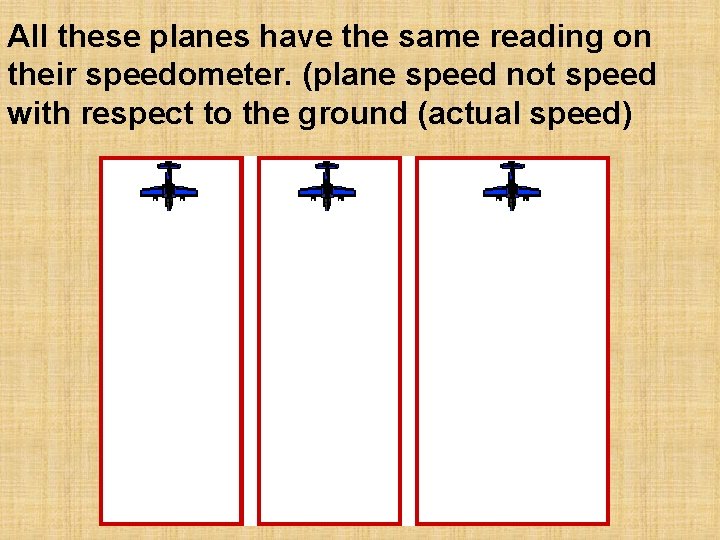
All these planes have the same reading on their speedometer. (plane speed not speed with respect to the ground (actual speed)

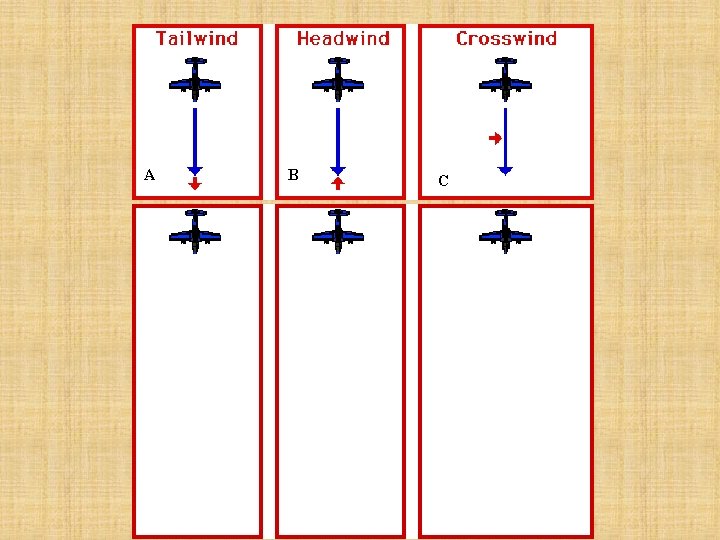
A B C

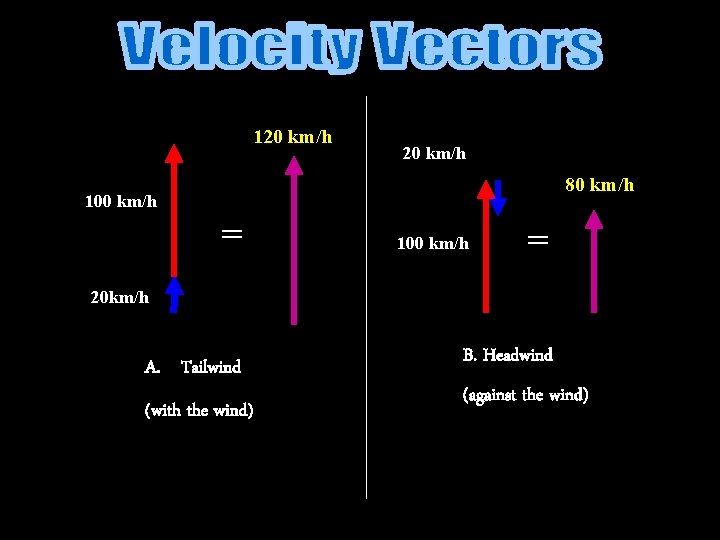
120 km/h 80 km/h 100 km/h = 20 km/h A. Tailwind (with the wind) B. Headwind (against the wind)

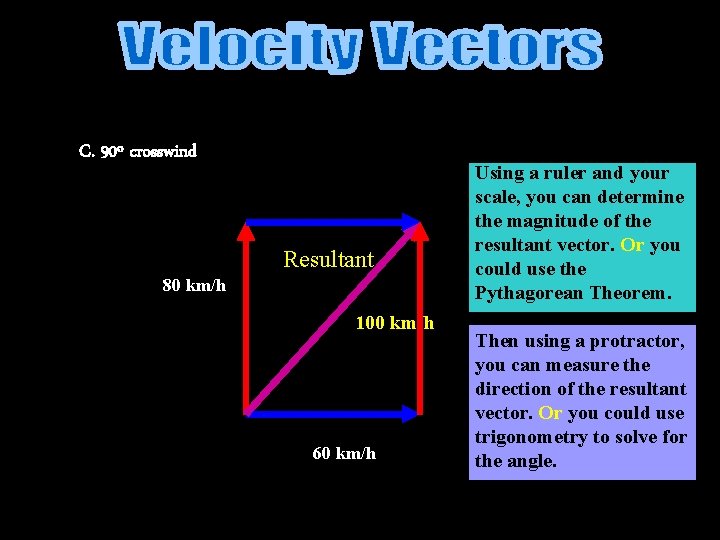
C. 90º crosswind Resultant 80 km/h 100 km/h 60 km/h Using a ruler and your scale, you can determine the magnitude of the resultant vector. Or you could use the Pythagorean Theorem. Then using a protractor, you can measure the direction of the resultant vector. Or you could use trigonometry to solve for the angle.

1. Find the resultant force vector of the two forces below. 25 N due East, 45 N due South 25 N, East Decide on a scale!!! 31º 51 E Nof S 51 N 59º S of E 45 N, South

o An airplane is flying 200 mph at 50 N of E. Wind velocity is 50 mph due S. What is the. N velocity of the plane? 180 o 0 o 270 o Scale: 50 mph = 1 inch

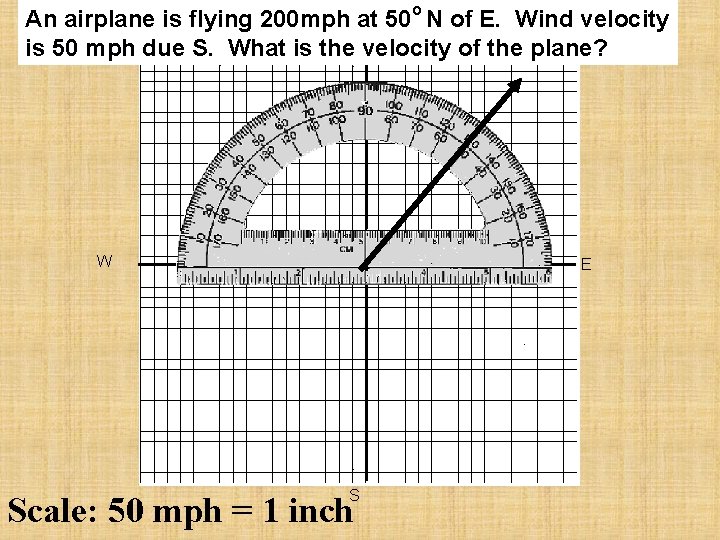
o An airplane is flying 200 mph at 50 N of E. Wind velocity is 50 mph due S. What is the. Nvelocity of the plane? W E S Scale: 50 mph = 1 inch

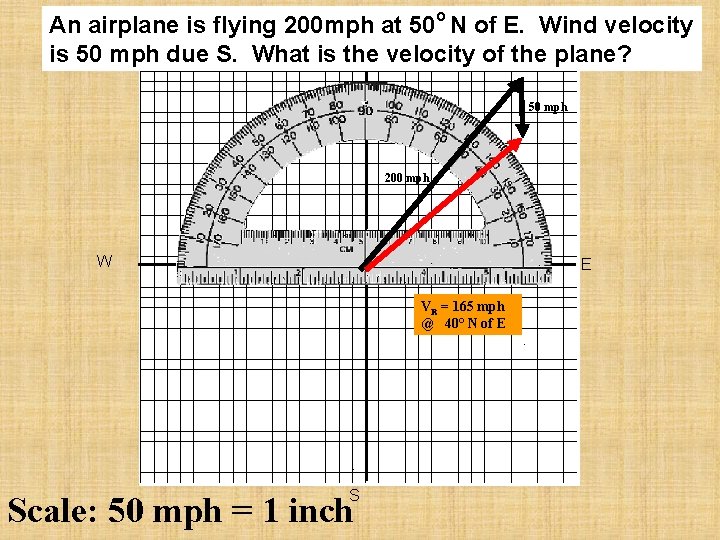
An airplane is flying 200 mph at 50 o N of E. Wind velocity N is 50 mph due S. What is the velocity of the plane? 50 mph 200 mph W E VR = 165 mph @ 40° N of E S Scale: 50 mph = 1 inch

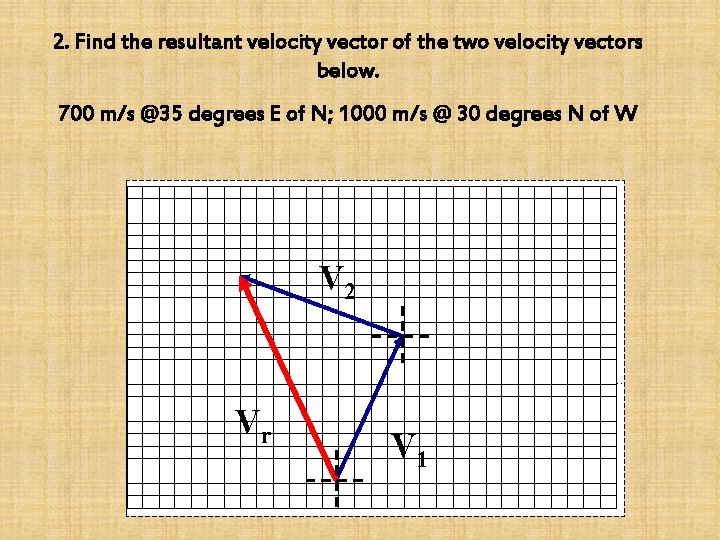
2. Find the resultant velocity vector of the two velocity vectors below. 700 m/s @35 degrees E of N; 1000 m/s @ 30 degrees N of W V 2 Vr V 1

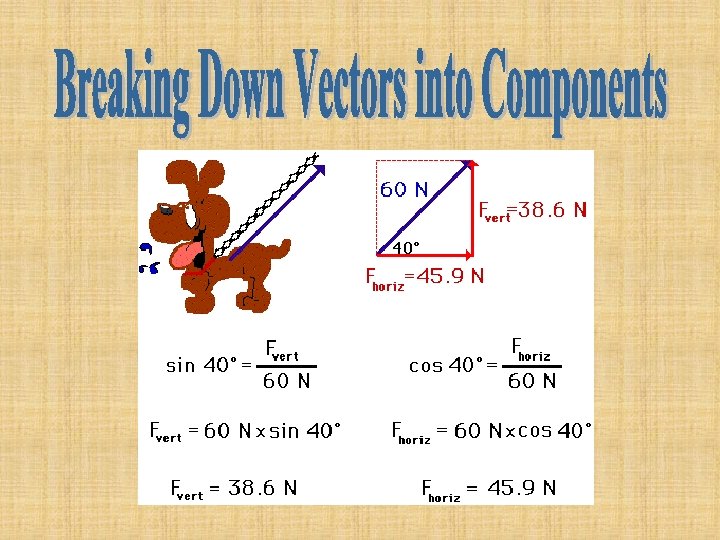
In what direction is the leash pulling on the dog?

What would happen to the upward and rightward Forces if the Force on the chain were smaller?

1) Find the resultant Magnitude: _____ 24. 99 N 34. 90º N of W of the two vectors. Direction: ______ Vector #1 = 20. 5 N West Vector #2 = 14. 3 N North Vector Diagram V 2 VR=? V 1

2) Find the component of the resultant = 255 m 27º South of East 115. 8 m Direction_____ South (-) Vector # 1 _______ East (+) 227. 2 m Direction_____ Vector # 2____ Vector Diagram: Conventions: V 2 Vr + V 1 - + -

Skip Practice: Find FR = Fnet =? 200 N due South, 100 N at 40º N of W 1. Draw vector diagram. (Draw axis) 2. Resolve vectors into components using trig: Vadj = V cos θ Vopp = V sin θ 3. Sum x and y components: ΣVxi ΣVyi 4. Redraw!! Determine resultant vector using Pythagorean’s Theorem and trig: Magnitude= √(Σ Vxi)² + (Σ Vyi)² Direction Action: θ = tan-1(opp/adj) Answer: Fnet = N @ ˚ W of S

An airplane flies at an engine speed of 100 m/s at 50º W of S into a wind of 30 m/s at 200 E of N. What is the airplane’s resultant velocity? Solve using the components method!! How far has the plane traveled after 1 hr? ? Answer: 75. 52 m/s @ 28. 54˚ S of W 168. 89 miles per 1 hour

You Try!!! A motor boat traveling 4. 0 m/s, East encounters a current traveling 3. 0 m/s, North. a. What is the resultant velocity of the motor boat? b. If the width of the river is 80 meters wide, then how much time does it take the boat to travel shore to shore? c. What distance downstream does the boat reach the opposite shore?

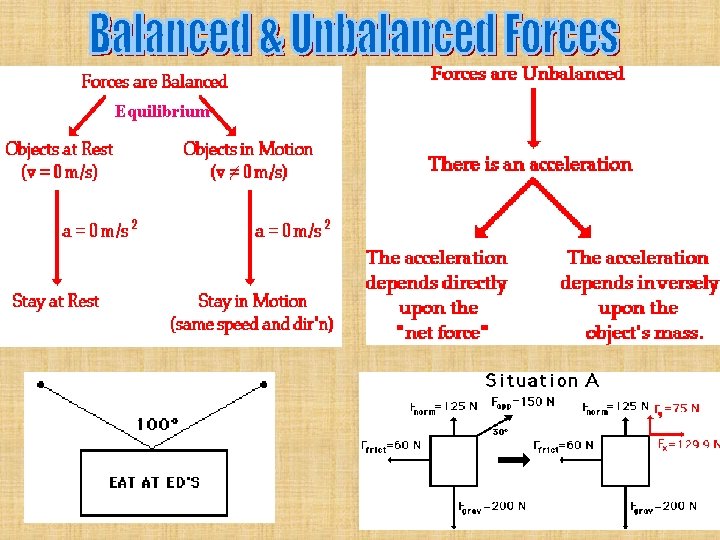
Equilibrium

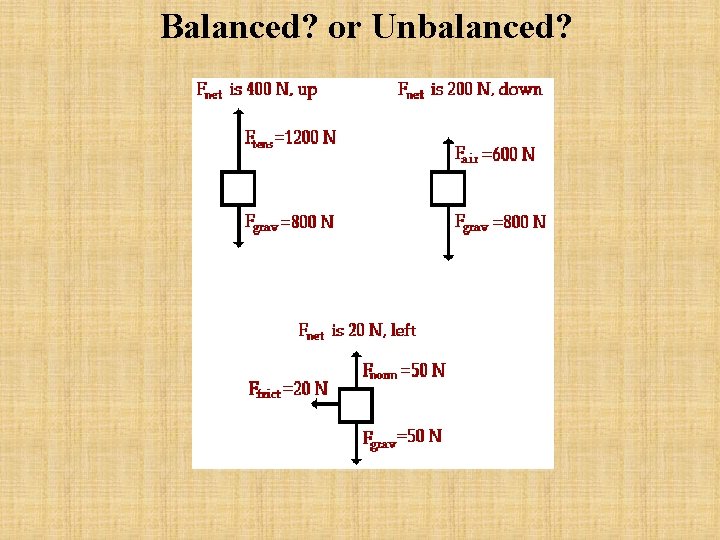
Balanced? or Unbalanced?

Forces are in Equilibrium

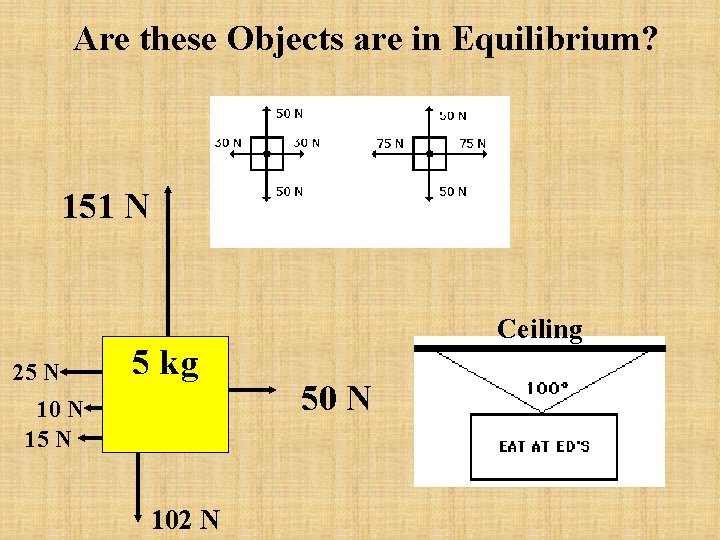
Are these Objects are in Equilibrium? 151 N 25 N 5 kg 10 N 15 N 102 N Ceiling 50 N

The First Condition of Equilibrium: The upward forces must balance the downward forces, and the leftward forces must balance the rightward forces. SFx = 0 SFy = 0 at equilibrium Solution of Problems in Static's: 1) Isolate a body. What point or object are you going to talk about? 2) Draw the forces acting on the body you have isolated, and label them. (If their value is not know, give them a symbol such as F 1, FP, T 1, etc. ) Remember…this is a free-body diag.

Cont. 3) Split each of the forces into its x and y components, and label the components in terms of the symbols given in rule 2 and the proper sines and cosines. 4) Write down your summation equations for the first condition of equilibrium. 5) Solve the equations for the unknowns.

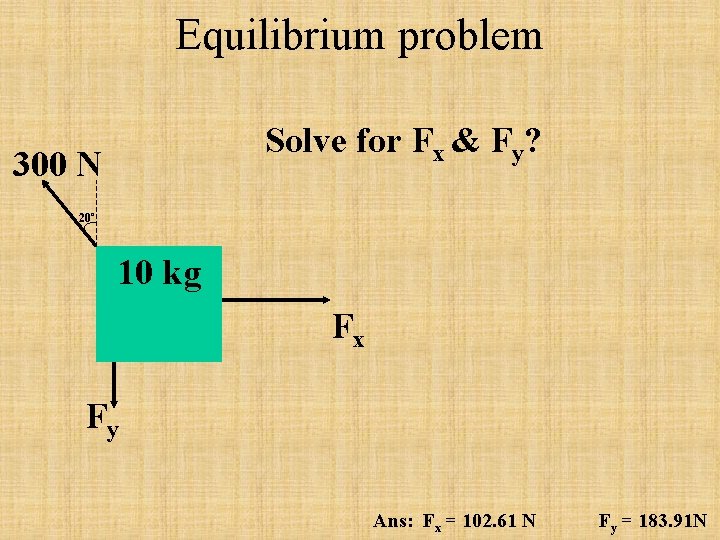
Equilibrium problem Solve for Fx & Fy? 300 N 20º 10 kg Fx Fy Ans: Fx = 102. 61 N Fy = 183. 91 N

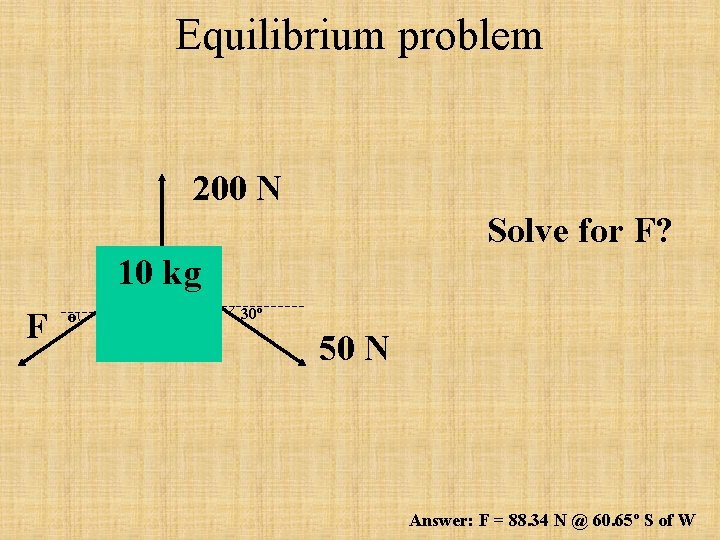
Equilibrium problem 200 N Solve for F? 10 kg F ө 30º 50 N Answer: F = 88. 34 N @ 60. 65º S of W

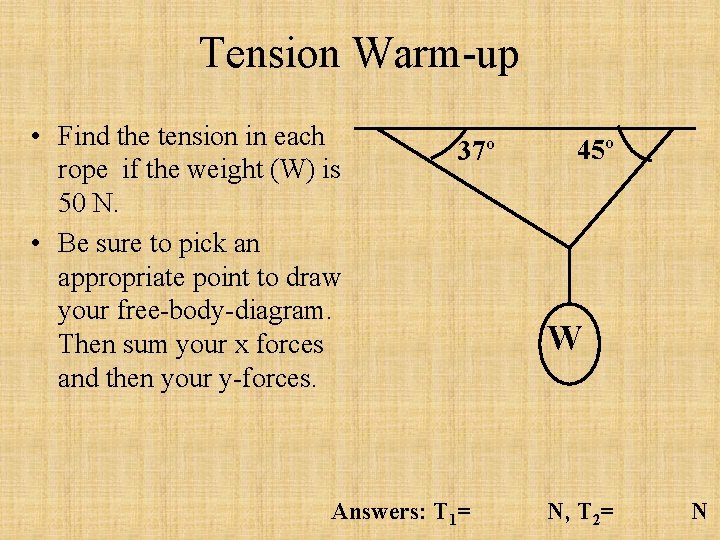
Tension Warm-up • Find the tension in each rope if the weight (W) is 50 N. • Be sure to pick an appropriate point to draw your free-body-diagram. Then sum your x forces and then your y-forces. 37º Answers: T 1= 45º W N, T 2= N

When the strongman suspends the 10 N telephone book with the rope held vertically the tension in each strand of rope is 5 N. If the strongman could suspend the book from the strands pulled horizontally as shown, the tension in each strand would be: a) About 5 N b) About 10 N c) About 20 N d) More than a million Newtons. . . basically impossible.

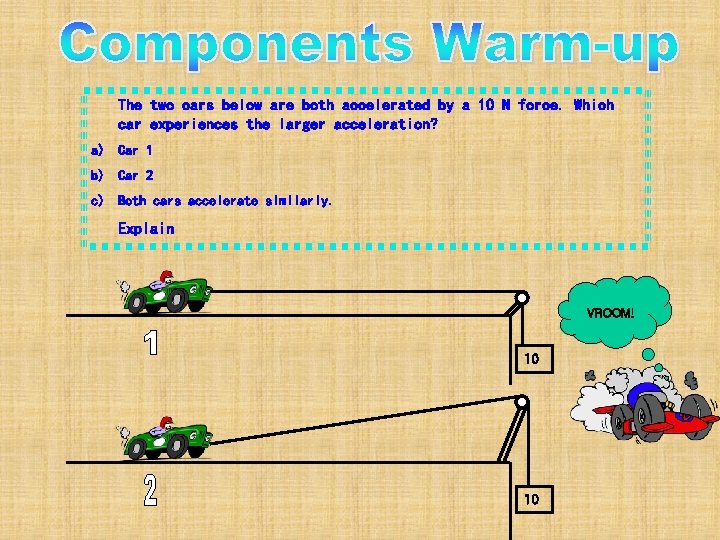
The two cars below are both accelerated by a 10 N force. Which car experiences the larger acceleration? a) Car 1 b) Car 2 c) Both cars accelerate similarly. Explain VROOM! 10 10