Vectors and Scalars Vector Addition Scalar A SCALAR

Vectors and Scalars Vector Addition

Scalar A SCALAR is ANY quantity in physics that has MAGNITUDE, but NOT a direction associated with it. Magnitude – A numerical value with units. Scalar Example Magnitude Speed 20 m/s Distance 10 m Age 15 years

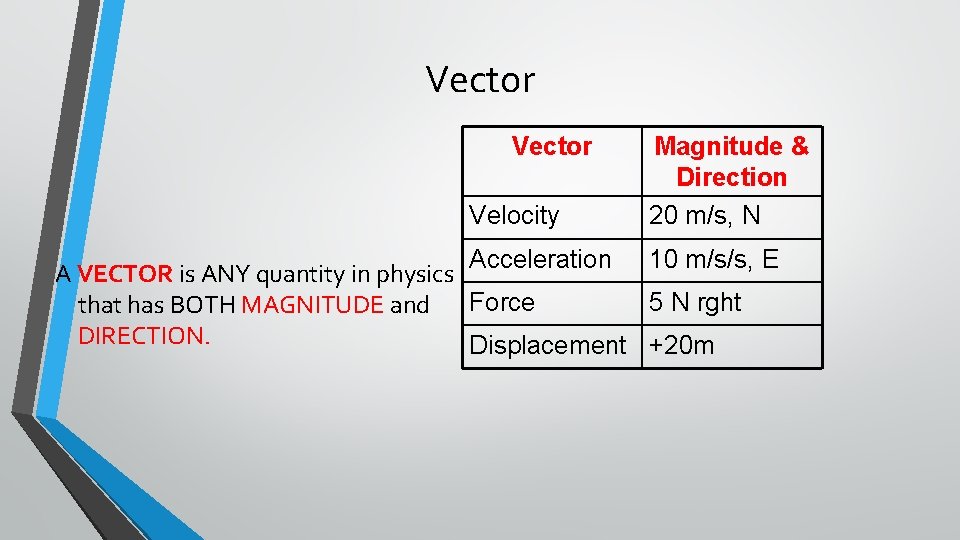
Vector Velocity Magnitude & Direction 20 m/s, N Acceleration 10 m/s/s, E A VECTOR is ANY quantity in physics Force 5 N rght that has BOTH MAGNITUDE and DIRECTION. Displacement +20 m

Applications of Vectors Example #1: A man walks 50 m east, then another 30 m east. Calculate his displacement relative to where he started? REPRESENTING VECTORS – ARROW tail head VECTOR ADDITION – Use the head to tail method Make a Vector Diagram (a picture that shows the given vectors in aproblem) and solve using Equations. 1) draw one vector 2) connect the tail of the 2 nd vector to the head of 1 st vector 3) Draw a 3 rd vector (resultant – final vector) from the tail of the 1 st vector to head of the 2 nd vector ∆d 1 = 50 m, E ∆d 2 = 30 m, E ∆dt = ∆d 1 + ∆d 2 = (+50 m) + (+30 m) ∆dt = +80 m or 80 m E Notice that the SIZE of the arrow conveys MAGNITUDE and the way it was drawn conveys DIRECTION.

Applications of Vectors • Example #2: A man walks 50 m east, then 30 m west. Calculate his displacement relative to where he started? 50 m, E 20, E 30 m, W ∆dt = ∆d 1 + ∆d 2 = (+50 m) + (-30 m) = +20 m or 20 m E

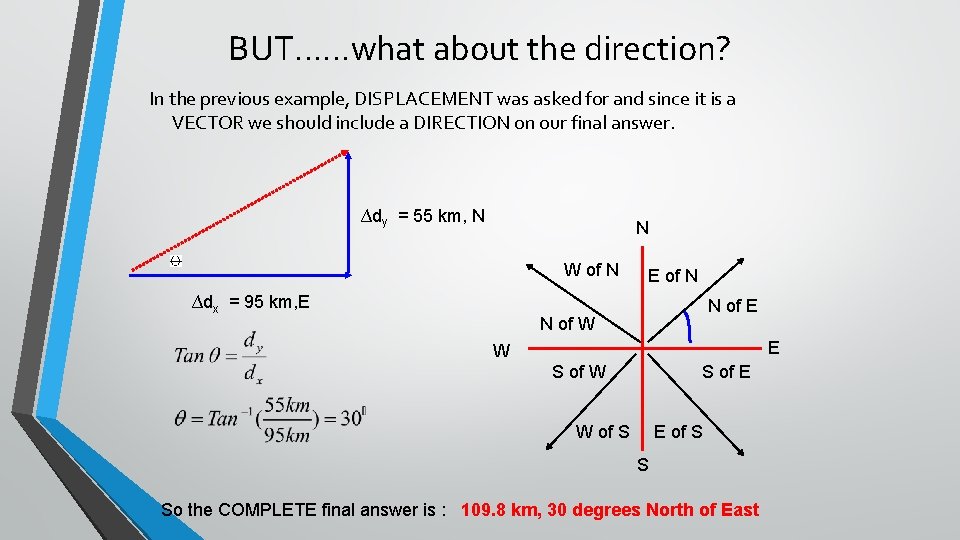
Perpendicular Vectors When 2 vectors are perpendicular, you must use the Pythagorean theorem. Example #3: A man walks 95 km, East then 55 km, north. Calculate his RESULTANT DISPLACEMENT. T. N A LT U S E ∆d t =R Horizontal Component Finish ∆dy = 55 km, N Vertical Component ∆dx = 95 km, E Start The LEGS of the triangle are called the COMPONENTS

BUT……what about the direction? In the previous example, DISPLACEMENT was asked for and since it is a VECTOR we should include a DIRECTION on our final answer. ∆dy = 55 km, N N W of N ∆dx = 95 km, E E of N N of E N of W E W S of E W of S E of S S So the COMPLETE final answer is : 109. 8 km, 30 degrees North of East

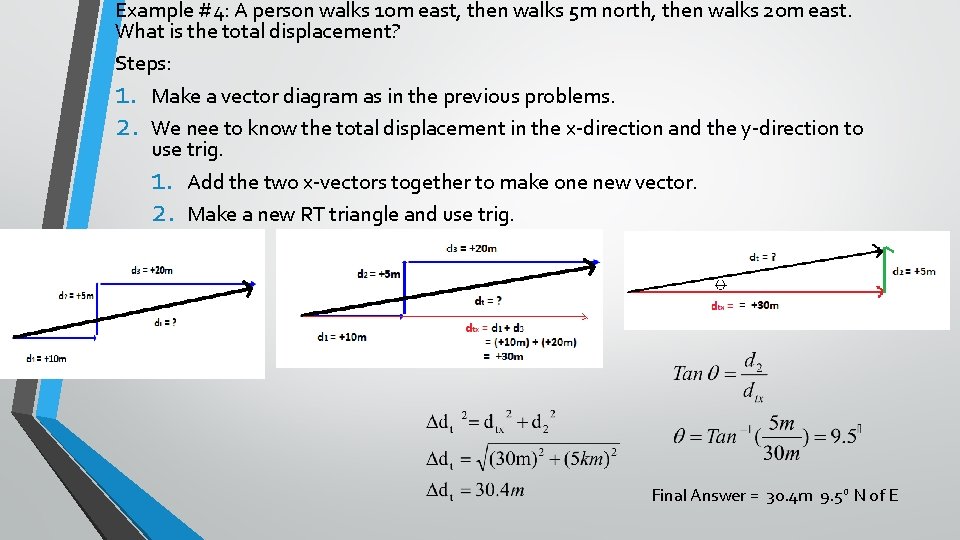
Example #4: A person walks 10 m east, then walks 5 m north, then walks 20 m east. What is the total displacement? Steps: 1. Make a vector diagram as in the previous problems. 2. We nee to know the total displacement in the x-direction and the y-direction to use trig. 1. Add the two x-vectors together to make one new vector. 2. Make a new RT triangle and use trig. Final Answer = 30. 4 m 9. 5 o N of E