Vectors and Scalars Distance how far an object

Vectors and Scalars Distance – how far an object moves - expressed as a magnitude (size) Ex – I drove 10 miles. Displacement – distance traveled in a particular direction - also expresses location relative to a starting point - expressed as a magnitude and direction Ex – I drove 10 miles south.

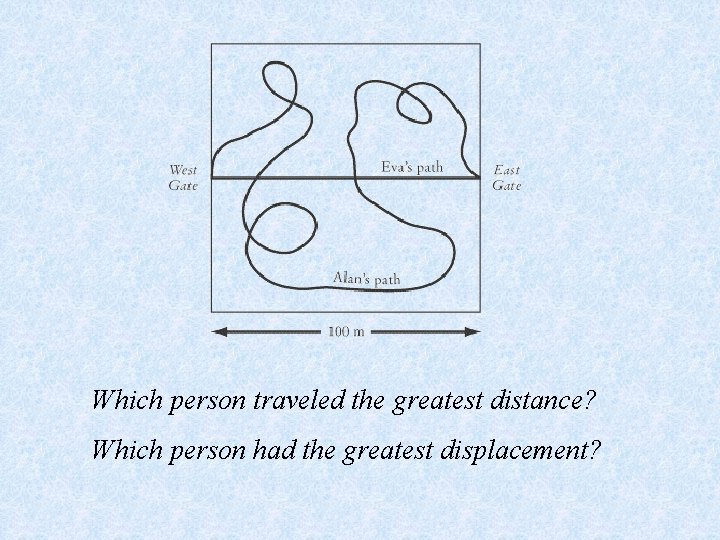
Which person traveled the greatest distance? Which person had the greatest displacement?

All physics quantities fall into one of two categories: Scalar – a quantity that can be described with a single number (size, magnitude). Ex. Distance, time, temp Vector – a quantity that includes a number and a direction. Ex. Displacement, force, velocity

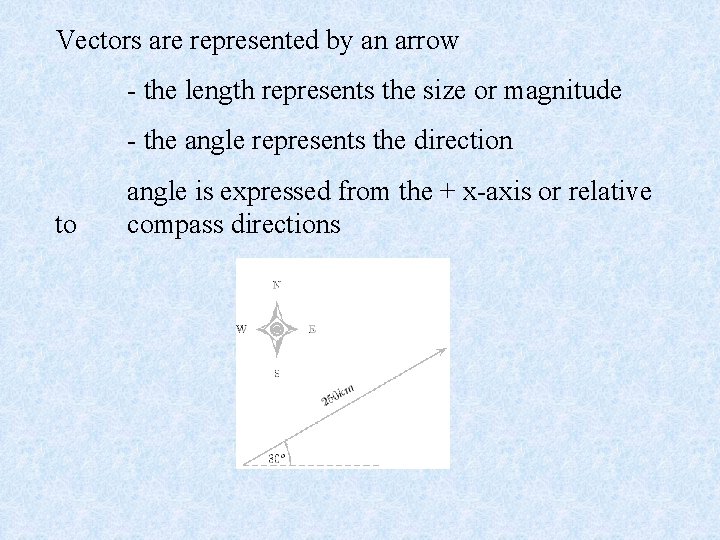
Vectors are represented by an arrow - the length represents the size or magnitude - the angle represents the direction to angle is expressed from the + x-axis or relative compass directions

Polar form: expressed in magnitude and direction A = (10 mi, 53 o) Cartesian form: expressed in x and y components Ax = 6 mi, Ay = 8 mi A = 6 i + 8 j

Convert the following to their opposite form: A=-4 i– 6 j B x = 8, B y = -10 C = (20, 210 o) D = 10, 30 o west of south

Vector Addition: Resultant: the term given for the final sum vector when adding 2 or more vectors together Question: 4 cm + 5 cm = ? WRONG!!! 4 cm north + 5 cm north = ? 9 cm north 4 cm north + 5 cm south = ? 1 cm south Adding vectors that are in the same or opposite directions is easy.

Adding vectors that are coplanar but are not in the same or opposite directions requires scaled diagrams. A man runs 8 mi east and 6 miles south. What is his displacement?

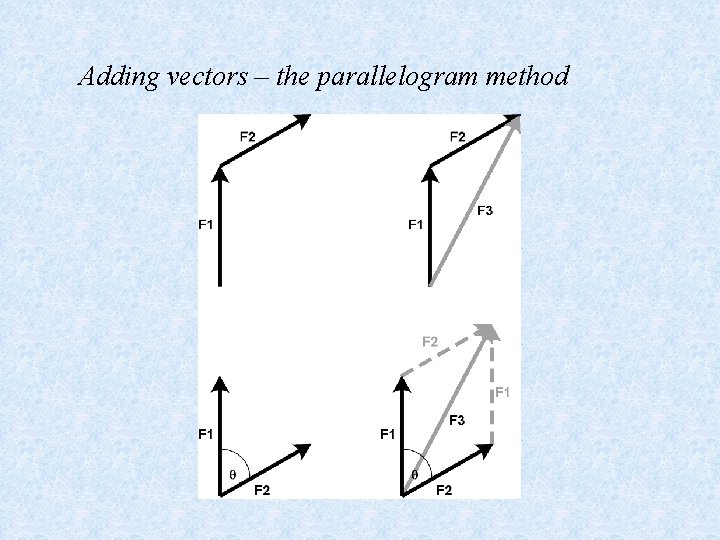
Adding vectors – the parallelogram method

A = (10 m, 45 o) B = (5 m, 210 o) A+B=? A–B=? 2 A = ?

A postal employee drives a truck 1 mi north, then 2 mi east, then 5 mi northwest. Determine the magnitude and direction of the resultant displacement.

A spelunker follows a passage 100 m east, then 50 m in a direction 30 o west of north, then 150 m southwest. After a fourth unmeasured displacement he finds himself back where he started. Determine the magnitude and direction of the fourth displacement.

A boat sails 3 km east, 10 km southwest and an unidentified displacement. Find the unknown displacement (magnitude and direction) if the boat ends up 6 km northwest of its starting point. 11. 31 km, 91 o

3 D Vectors A=3 i+4 j+5 k How else can we express this vector? Can we add it to another vector? B = -2 i -3 j + 4 k What is the resultant of A + B? What is its magnitude?

A flying rabbit undergoes two displacements. A=2 i– 3 j– 6 k B=-4 i+6 j+2 k a)How far is the rabbit from where it started? b)What total distance did it fly?

2 -1) A = 8. 7 i + 5 j B=3 i+4 j C = 6 i – 10. 4 j D = -16 i + 12 j E = -6. 9 i -4 j

2 -1) a) A + B = 11. 7 i + 9 j = (14. 8, 38 o) b)B + C = 9 i – 6. 4 j = (11, -35 o) c) D + E = -22. 9 i + 8 j = (24, 161 o) d)A – B = 5. 7 i + 1 j (5. 79, 9. 95 o) e) D – E = -9. 1 i + 16 j = (18. 4, 119. 6 o) f) A + 2 E = -5. 1 i – 3 j = (5. 9, 210 o)

2 -2) A = 0 i + 40 j B = - 20 i + 0 j C = 42. 4 i + 42. 4 j D = 0 i + 50 j A+B+C+D = 22. 4 i + 132. 4 j

2 -3) A+B+C+D = 22. 4 i E= xi + R= - 50 i + + 132. 4 j yj 0 j E = R – (A+B+C+D) = - 72. 4 i – 132. 4 j

2 -13) d 1 = 3 i - 4 j – 2 k d 2 = 1 i – 7 j + 4 k d 3 = -7 i + 4 j + 1 k a) R = - 3 i – 7 j + 3 k b) |R| = 8. 2

2 -13) c) |d 1| = 5. 4 |d 2| = 8. 1 |d 3| = 8. 1 Distance = 22 cm

The radius and mass of the sun 8 are approximately 7 x 10 m and 2 x 1030 kg respectively. What is the mass density of the sun in slugs per cubic inch?