Vectors and Scalars Copyright John OConnor St Farnans

Scalars A scalar quantity is a quantity that has magnitude only and has no

Vectors A vector quantity is a quantity that has both magnitude and a direction

Vector Diagrams Vector diagrams are shown using an arrow The length of the arrow

Resultant of Two Vectors The resultant is the sum or the combined effect of

The Parallelogram Law When two vectors are joined tail to tail Complete the parallelogram

Problem: Resultant of 2 Vectors 2004 HL Section B Q 5 (a) Two forces

Problem: Resultant of 3 Vectors Find the magnitude (correct to two decimal places) and

Recap What is a scalar quantity? Give 2 examples What is a vector quantity?

Resolving a Vector Into Perpendicular Components Here a vector v is resolved into an

Practical Applications Here we see a table being pulled by a force of 50

Calculating the Magnitude of the Perpendicular Components If a vector of magnitude v and

Problem: Calculating the magnitude of perpendicular components 2002 HL Sample Paper Section B Q

2003 HL Section B Q 6 A person in a wheelchair is moving up

Summary If a vector of magnitude v has two perpendicular components x and y,

Slides: 15

Download presentation

Vectors and Scalars Copyright © John O’Connor St. Farnan’s PPS Prosperous For non-commercial purposes only…. . Enjoy! Comments/suggestions please to the SLSS physics website forum @ http: //physics. slss. ie/forum

Scalars A scalar quantity is a quantity that has magnitude only and has no direction in space Examples of Scalar Quantities: Length Area Volume Time Mass

Vectors A vector quantity is a quantity that has both magnitude and a direction in space Examples of Vector Quantities: Displacement Velocity Acceleration Force

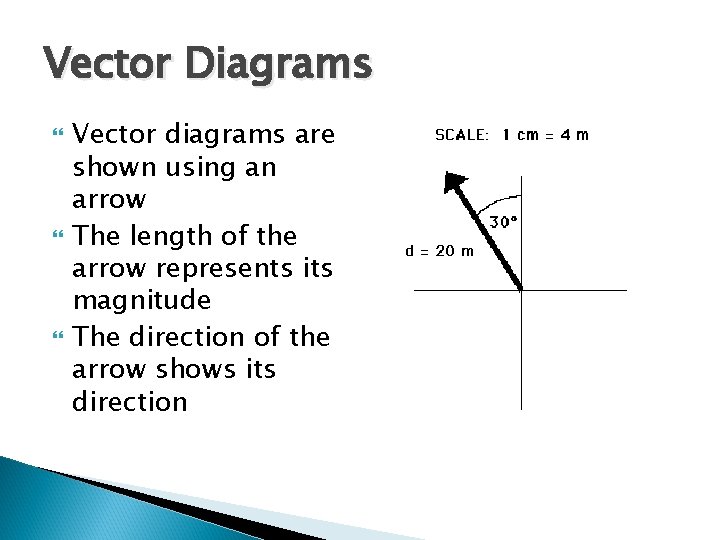
Vector Diagrams Vector diagrams are shown using an arrow The length of the arrow represents its magnitude The direction of the arrow shows its direction

Resultant of Two Vectors The resultant is the sum or the combined effect of two vector quantities Vectors in the same direction: 6 N 6 m 4 m 4 N = 10 m Vectors in opposite directions: 6 m s-1 10 m s-1 = 4 m s-1 6 N 10 N = 4 N

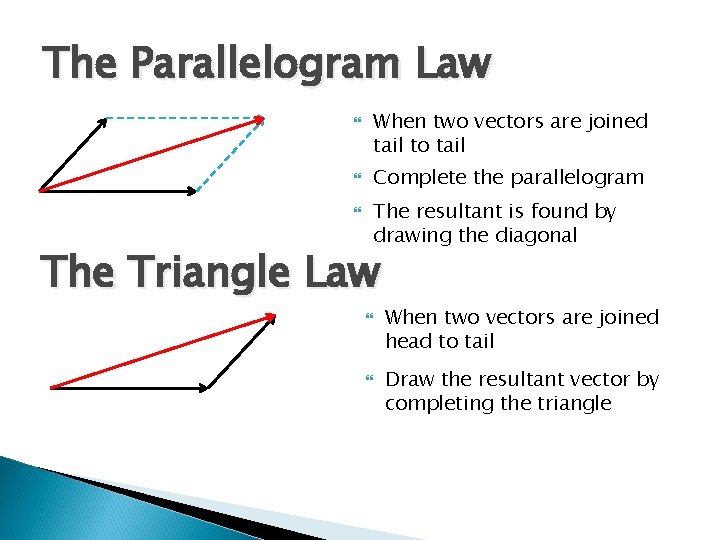
The Parallelogram Law When two vectors are joined tail to tail Complete the parallelogram The resultant is found by drawing the diagonal The Triangle Law When two vectors are joined head to tail Draw the resultant vector by completing the triangle

Problem: Resultant of 2 Vectors 2004 HL Section B Q 5 (a) Two forces are applied to a body, as shown. What is the magnitude and direction of the resultant force acting on the body? Solution: Complete the parallelogram (rectangle) The diagonal of the parallelogram ac represents the resultant force The magnitude of the resultant is found using Pythagoras’ Theorem on the triangle abc a 5 N b θ 12 N 13 12 d N 5 c Resultant displacement is 13 N 67º with the 5 N force

Problem: Resultant of 3 Vectors Find the magnitude (correct to two decimal places) and direction of the resultant of the three forces shown below. Solution: Find the resultant of the two 5 N forces first (do right angles first) 5 So, Resultant = 10 N – 7. 07 N = 2. 93 N in the direction of the 10 N force 7. 07 5 N a N 93 N 2. Now find the resultant of the 10 N and 7. 07 N forces The 2 forces are in a straight line (45º + 135º = 180º) and in opposite directions 10 N d 90º θ 45º 135º 5 N c 5 b

Recap What is a scalar quantity? Give 2 examples What is a vector quantity? Give 2 examples How are vectors represented? What is the resultant of 2 vector quantities? What is the triangle law? What is the parallelogram law?

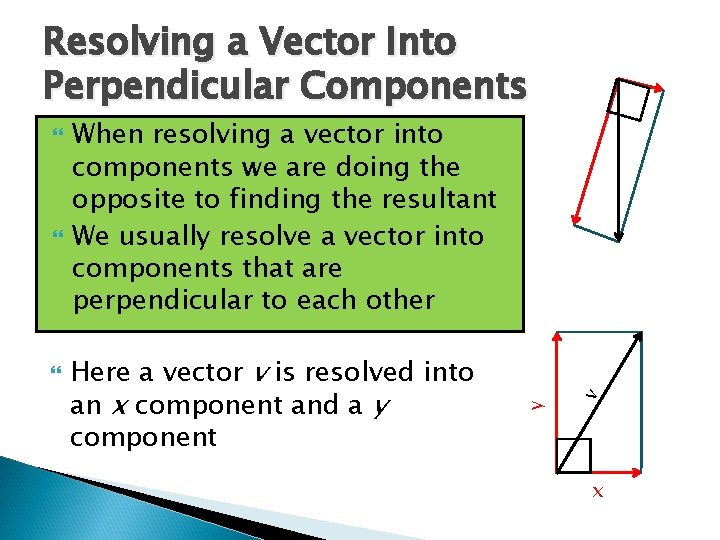
Resolving a Vector Into Perpendicular Components Here a vector v is resolved into an x component and a y component v When resolving a vector into components we are doing the opposite to finding the resultant We usually resolve a vector into components that are perpendicular to each other y x

Practical Applications Here we see a table being pulled by a force of 50 N at a 30º angle to the horizontal When resolved we see that this is the same as pulling the table up with a force of 25 N and pulling it horizontally with a force of 43. 3 N y=25 N 50 N 30º x=43. 3 N We can see that it would be more efficient to pull the table with a horizontal force of 50 N

Calculating the Magnitude of the Perpendicular Components If a vector of magnitude v and makes an angle θ with the horizontal then the magnitude of the components are: v y=v Sin θ x = v Cos θ y = v Sin θ Proof: x=vx Cos θ

Problem: Calculating the magnitude of perpendicular components 2002 HL Sample Paper Section B Q 5 (a) A force of 15 N acts on a box as shown. What is the horizontal component of the force? 15 N Vertical 12. 99 N Component Solution: 60º Horizontal 7. 5 N Component

2003 HL Section B Q 6 A person in a wheelchair is moving up a ramp at constant speed. Their total weight is 900 N. The ramp makes an angle of 10º with the horizontal. Calculate the force required to keep the wheelchair moving at constant speed up the ramp. (You may ignore the effects of friction). Solution: If the wheelchair is moving at constant speed (no acceleration), then the force that moves it up the ramp must be the same as the component of it’s weight parallel to the ramp. Complete the parallelogram. Component of weight 28 N. 6 5 1 10º parallel to ramp: 80º Component of weight perpendicular to ramp: 10º 900 N 886. 33 N

Summary If a vector of magnitude v has two perpendicular components x and y, and v makes and angle θ with the x component then the magnitude of the components are: x= v Cos θ y= v Sin θ v y=v Sin θ θ x=v Cosθ y