Vectors and Matrices Class 17 1 E Ch

Vectors and Matrices Class 17. 1 E: Ch. 5

Objectives Know what a Cartesian coordinate system is. Know the difference between a scalar and a vector. Review/learn how to interpret, add, subtract, and find the magnitude of vectors n Know how to use the right hand rule.

Objectives Be able to calculate the determinant of a matrix. Be able to calculate the dot and cross products of vectors Be able to represent a system of linear equations as matrices and vectors. Be able to solve systems of linear equations using matrices.

Cartesian Coordinates The Cartesian coordinate system is a system of orthogonal axes which is the basis for describing body and force systems in mechanics. n z n The coordinate system is always right handed (obeys the right hand rule. We will focus on 2 D systems. y x 4

Scalars and Vectors A scalar is a physical quantity having magnitude but not direction n Length, mass, time A vector is a physical quantity having both magnitude and direction n Force, velocity, acceleration 5

Vectors have components along axes of the Cartesian system n x, y, and z axes are denoted by unit vectors w carat often used to imply unit vector w Unit vectors have a magnitude (length) of one. z b a c x y 6

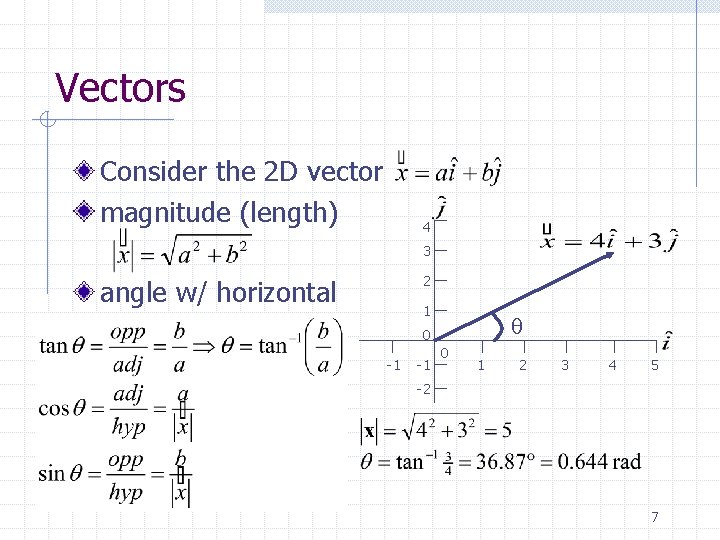
Vectors Consider the 2 D vector magnitude (length) 4 3 2 angle w/ horizontal 1 q 0 -1 -1 0 1 2 3 4 5 -2 7

Dot Product Dot product is a vector operation. n Dot product of matrices does not exist. The result is a scalar. Using tools: n n TI-83, 86: dot TI-89: dotp Maple: dotprod Matlab: dot

Dot Product: Consider the 2 D case: Plot these vectors.

Vector Addition & Subtraction When adding, treat each direction separately 4 To add, place vectors head to tail The negative of a vector is simply pointing in the opposite direction The sum of vectors is called the resultant. 3 2 1 q 0 -1 -1 0 1 2 3 4 5 -2 10

Matrix and Vector A matrix is an n x m array of numbers n n rows, m columns n The ij-th element, aij, is the element in row i and column j A vector is a matrix that has only one row or only one column 11

Basic Functions The transpose is obtained by swapping columns and rows n In Matlab: apostrophe The addition operation requires dimensional agreement. n i. e. to add a m x n matrix and a q x r matrix, must have m = q and n = r Matrix addition is done by corresponding element 12

Matrix Multiplication Matrix multiplication requires innerdimensional agreement n i. e. to multiply a m x n matrix and a q x r matrix, must have n = q Matrix multiplication is done by summing elementwise multiplication of row i in the first matrix with column j of the second matrix to get the ij-th element of the product. 13

Matrix Multiplication 14

Determinant The determinant operation applies to a square matrix (# rows = # columns) n n Denoted with bars 2 x 2 case:

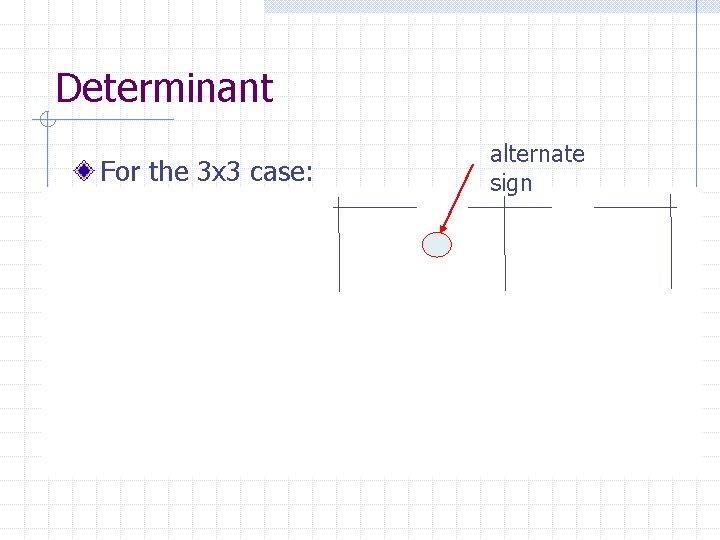
Determinant For the 3 x 3 case: alternate sign

Determinant For higher order cases uses tools. n n TI-86, 89: det Maple: > with(linalg); > det([[1, 5, 7], [2, 4, 8], [3, 6, 9]]); n Matlab: det

Cross Product The cross product is a vector operation n yields a vector according to the right-hand-rule n Also have:

Cross Product Example: Using your tools. n n TI-89: crossp([1, 5, 7], [2, 4, 8]) Maple: > with(linalg); > crossprod([[1, 5, 7], [2, 4, 8]); n Matlab: cross([1 5 7], [2 4 8])

Inverse A matrix times its inverse equals the identity matrix n Identity: All elements on the main diagonal are 1, all others are 0; matrix version of the scalar 1. n Matrix division is undefined Using TI-89: ([[1, 5, 7][2, 4, 8][3, 6, 9]])^-1 Matlab: inv([1, 5, 7; 2, 4, 8; 3, 6, 9]); Using Maple: inverse([[1, 5, 7], [2, 4, 8], [3, 6, 9]]); A-1 =

Linear Equations A linear equation is of the form: where the ai’s are constants (coefficients) In order to solve for n unknowns (xn), n independent equations are needed.

2 Equations, 2 Unknowns Consider the system of equations: 3 things can happen: n n n Exactly one solution (lines intersect) independent No solution (lines are parallel) Infinite number of solutions (same line)

Solving Systems of Equations Consider a system of 3 eqns, 3 unknowns: This can be written as: x= Using inverses can only be used if there is a single, unique solution; If multiple or no solutions exist, the inverse does not exist

Solving Systems of Equations Using your tools: Using Maple: multiply(inverse([[2, 4, 4], [1, 2, 1], [3, 4, 2]]), [[12], [4], [1]]); Using TI-89 (([[1, 5, 7], [2, 4, 8], [3, 6, 9]])^-1)*([12; 4; 1]) Or use ‘solve’ Using Matlab: inv ([2, 4, 4; 1, 2, 1; 3, 4, -2])*[12; 4; 1]);

Homework Web. Assign Your documentation of your homework is 20% of your webassignment grade. Homework documentation is due at the beginning of class when the webassign homework is due. If webassign is not due at the beginning of a class, your documentation is due at the beginning of the immediate next class or lab. If you need a refresher on problem presentation, read Ch. 2 in Eide