Vectors Addition Subtraction Graphical Analytical What is a

Vectors Addition & Subtraction Graphical & Analytical

What is a Vector? • A quantity that requires magnitude and direction to completely describe it is a vector. • An arrow is used to represent a vector. The length of the arrow represents the magnitude. • Some examples of vectors are: displacement, velocity, acceleration, force, momentum • Some examples of non-vectors (scalars) are: distance, speed, work, energy

Vector Addition • When two or more vectors are added the directions must be considered. • Vectors may be added Graphically or Analytically. • Graphical Addition requires the use of rulers and protractors to make scale drawings of vectors tip-to-tail. (Less accurate) • Analytical Addition is a strictly mathematical method using trigonometric functions (sin, cos, tan) to add the vectors together.

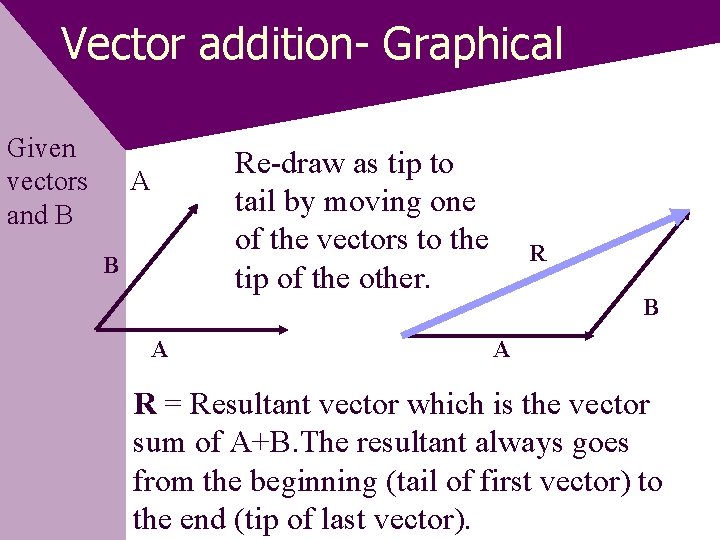
Vector addition- Graphical Given vectors and B Re-draw as tip to tail by moving one of the vectors to the tip of the other. A B A R = Resultant vector which is the vector sum of A+B. The resultant always goes from the beginning (tail of first vector) to the end (tip of last vector).

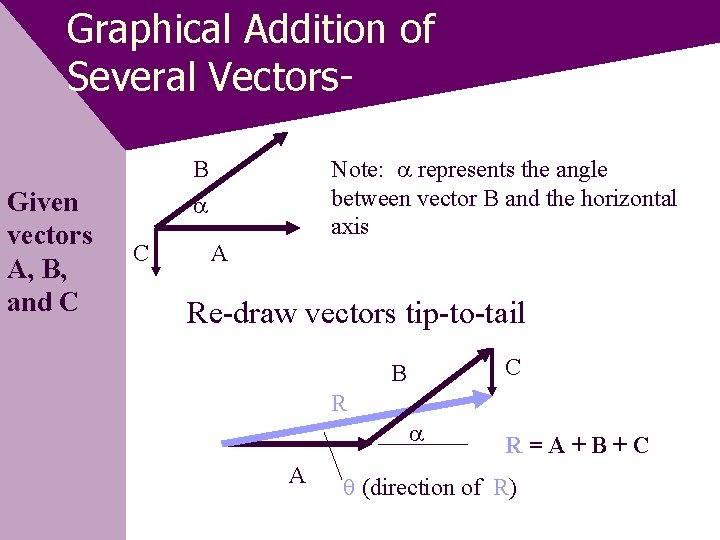
Graphical Addition of Several Vectors. Note: represents the angle between vector B and the horizontal axis B Given vectors A, B, and C C A Re-draw vectors tip-to-tail C B R A R=A+B+C (direction of R)

Vector Subtraction • To subtract vectors, add a negative vector. • A negative vector has the same magnitude and the opposite direction. Example: A -A Note: A + (-A) = 0

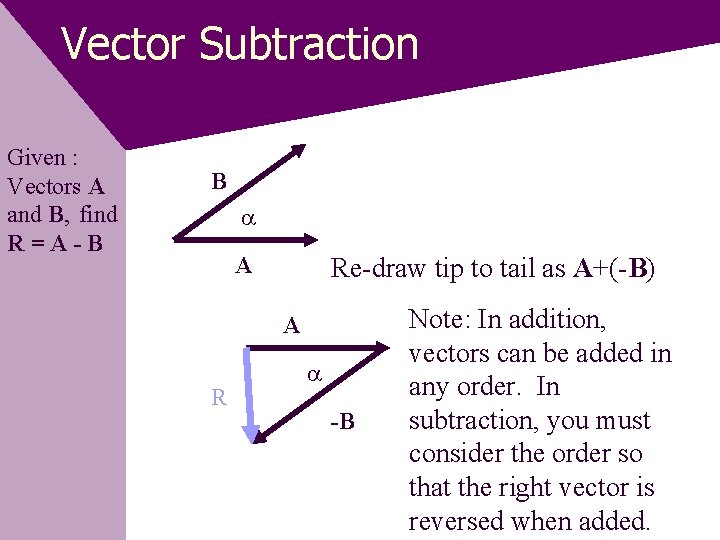
Vector Subtraction Given : Vectors A and B, find R=A-B B A Re-draw tip to tail as A+(-B) A R -B Note: In addition, vectors can be added in any order. In subtraction, you must consider the order so that the right vector is reversed when added.

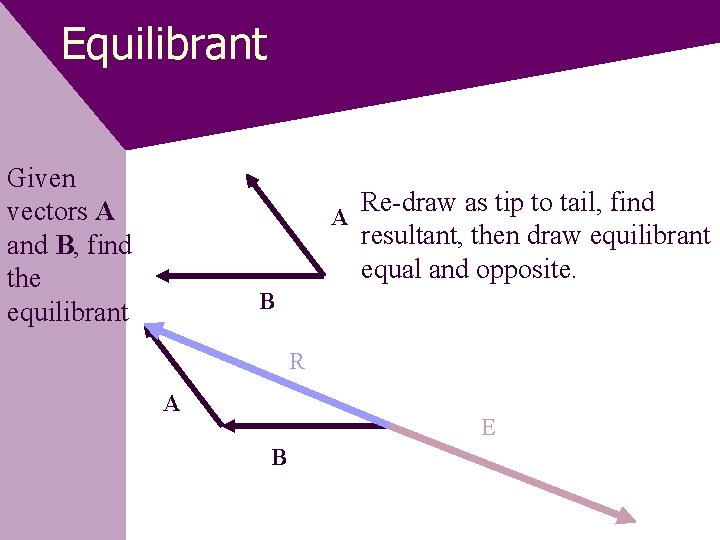
Equilibrant Given vectors A and B, find the equilibrant Re-draw as tip to tail, find A resultant, then draw equilibrant equal and opposite. B R A E B

Equilibrant • The equilibrant vector is the vector that will balance the combination of vectors given. • It is always equal in magnitude and opposite in direction to the resultant vector.

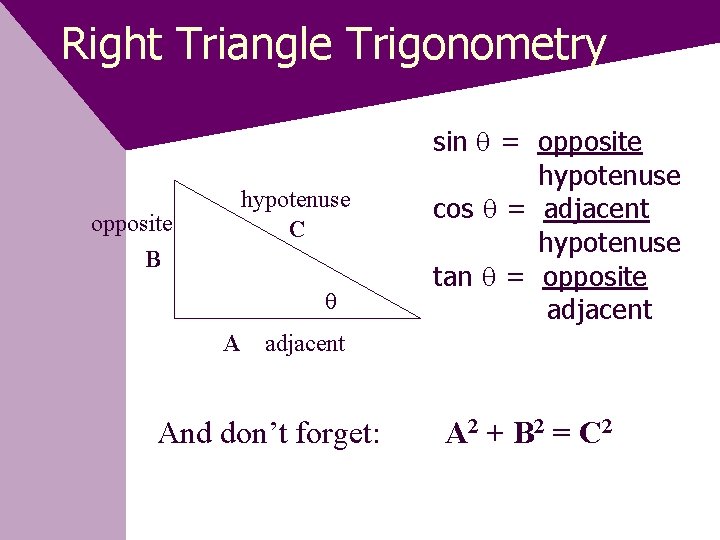
Right Triangle Trigonometry hypotenuse C opposite B A sin = opposite hypotenuse cos = adjacent hypotenuse tan = opposite adjacent And don’t forget: A 2 + B 2 = C 2

Vector Resolution Given: vector A at angle from horizontal. Resolve A into its components. (Ax and Ay) y A Ay x Ax Evaluate the triangle using sin and cos =Ax/A so… Ax = A cos sin = Ay/A so… Ay = A sin Hint: Be sure your calculator is in degrees!

Vector Addition-Analytical To add vectors mathematically: – resolve the vectors to be added into their x- and ycomponents. – Add the x- components together to get a resultant vector in the x direction – Add the y- components together to get a resultant vector in the y direction – Use the pythagorean theorem to add the resultant vectors in the x- and y-components together. – Use the tan function of your resultant triangle to find the direction of the resultant.

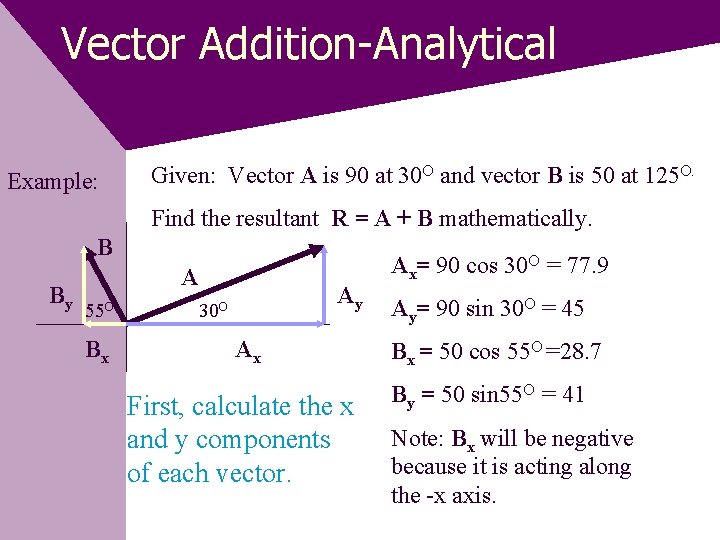
Vector Addition-Analytical Example: Given: Vector A is 90 at 30 O and vector B is 50 at 125 O. Find the resultant R = A + B mathematically. B By A 55 O Bx Ay 30 O Ax First, calculate the x and y components of each vector. Ax= 90 cos 30 O = 77. 9 Ay= 90 sin 30 O = 45 Bx = 50 cos 55 O =28. 7 By = 50 sin 55 O = 41 Note: Bx will be negative because it is acting along the -x axis.

Vector Addition-Analytical (continued) Find Rx and Ry: Rx = A x + B x R Ry Rx Ry = A y + B y Rx = 77. 9 - 28. 7 = 49. 2 Ry = 41 + 45 = 86 Then find R: R 2 = Rx 2 + Ry 2 R 2 = (49. 2)2+(86)2 , so… R = 99. 1 To find direction of R: = tan-1 ( Ry / Rx ) = tan-1 ( 86 / 49. 2 ) = 60. 2 O

Stating the final answer * ccw = counterclockwise cw = clockwise • All vectors must be stated with a magnitude and direction. • Angles must be specified according to compass directions( i. e. N of E) or adjusted to be measured from the +x-axis(0°). • The calculator will always give the angle measured from the closest horizontal axis. • CCW angles are +, CW are - *