Vector Space Text Classification Adapted from Lectures by

Vector Space Text Classification Adapted from Lectures by Raymond Mooney and Barbara Rosario Prasad L 14 Vector. Classify 1

Text Classification n Today: n Introduction to Text Classification n n K Nearest Neighbors Decision boundaries Vector space classification using centroids Decision Trees (briefly) Later n More text classification n n Prasad Support Vector Machines Text-specific issues in classification L 14 Vector. Classify 2

Recap: Naïve Bayes classifiers n Classify based on prior weight of class and conditional parameter for what each word says: n Training is done by counting and dividing: n Don’t forget to smooth 3

Recall: Vector Space Representation n Each document is a vector, one component for each term (= word). Normally normalize vector to unit length. High-dimensional vector space: n n Terms are axes 10, 000+ dimensions, or even 100, 000+ Docs are vectors in this space How can we do classification in this space? Prasad L 14 Vector. Classify 4 14. 1

Classification Using Vector Spaces n As before, the training set is a set of documents, each labeled with its class (e. g. , topic) In vector space classification, this set corresponds to a labeled set of points (or, equivalently, vectors) in the vector space Premise 1: Documents in the same class form a contiguous region of space Premise 2: Documents from different classes don’t overlap (much) n n We define surfaces to delineate classes in the space Prasad L 14 Vector. Classify 5

Documents / Classes in a Vector Space Government Science Arts Prasad L 14 Vector. Classify 6
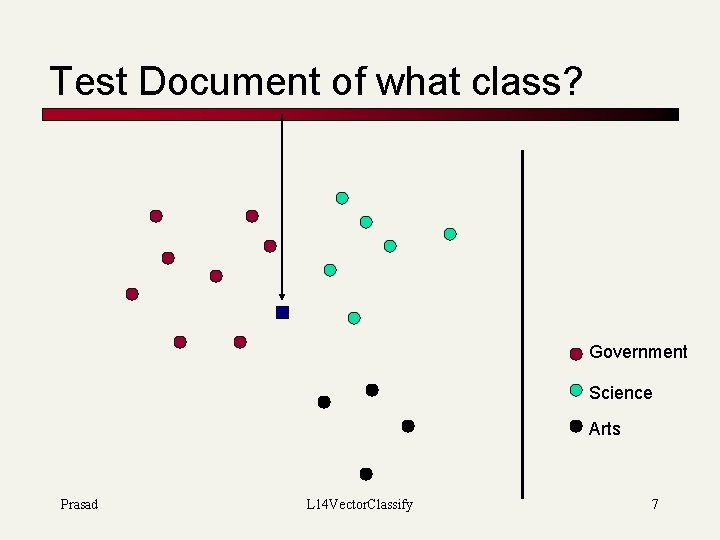
Test Document of what class? Government Science Arts Prasad L 14 Vector. Classify 7

Test Document = Government Is this similarity hypothesis true in general? Government Science Arts Our main topic today is how to find good separators 8

k Nearest Neighbor Classification Prasad L 14 Vector. Classify 9
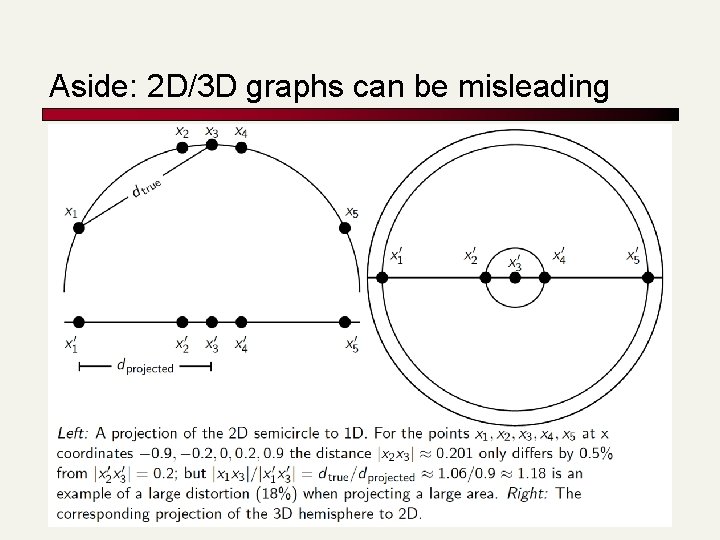
Aside: 2 D/3 D graphs can be misleading 10

k Nearest Neighbor Classification n k. NN = k Nearest Neighbor To classify document d into class c: n n Define k-neighborhood N as k nearest neighbors of d Count number of documents ic in N that belong to c Estimate P(c|d) as ic/k Choose as class arg maxc P(c|d) [ = majority class] Prasad L 14 Vector. Classify 11 14. 3
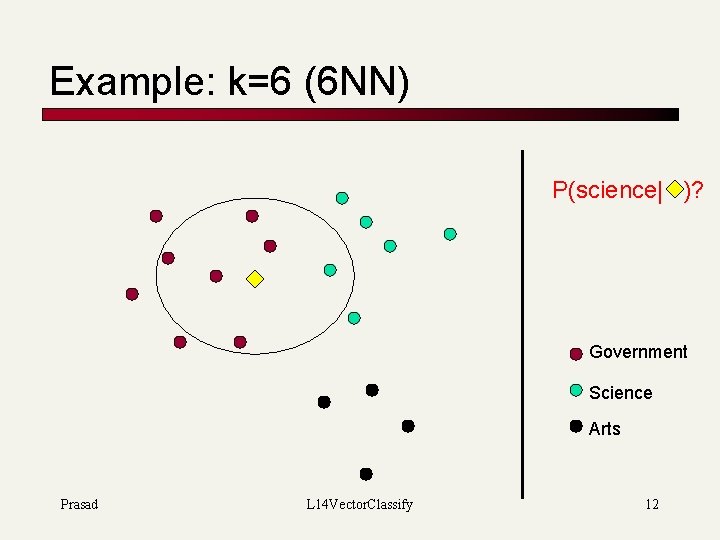
Example: k=6 (6 NN) P(science| )? Government Science Arts Prasad L 14 Vector. Classify 12

Nearest-Neighbor Learning Algorithm n Learning is just storing the representations of the training examples in D. n n Testing instance x: n n n Compute similarity between x and all examples in D. Assign x the category of the most similar example in D. Also called: n n Does not explicitly compute a generalization, category prototypes, or class boundaries. Case-based learning, Memory-based learning, Lazy learning Rationale of k. NN: contiguity hypothesis Prasad L 14 Vector. Classify 13

k. NN: Value of k n Using only the closest example (k=1) to determine the category is subject to errors due to: n n A single atypical example. Noise in the category label of a single training example. More robust alternative is to find the k (> 1) mostsimilar examples and return the majority category of these k examples. Value of k is typically odd to avoid ties; 3 and 5 are most common. Prasad L 14 Vector. Classify 14

Probabilistic k. NN 1 NN, 3 NN classification decision for star? 15

Exercise How is star classified by: (i) 1 -NN (ii) 3 -NN (iii) 9 -NN (iv) 15 -NN (v) Rocchio? 16

k. NN decision boundaries Boundaries are, in principle, arbitrary surfaces – but usually polyhedra Government Science Arts k. NN gives locally defined decision boundaries between classes – far away points do not influence each classification Prasad L 14 Vector. Classify decision (unlike in Naïve Bayes, Rocchio, etc. ) 17

k. NN is not a linear classifier § Classification decision based on majority of k nearest neighbors. §The decision boundaries between classes are piecewise linear. . . §. . . but they are in general not linear classifiers that can be described as 18

Similarity Metrics n Nearest neighbor method depends on a similarity (or distance) metric. n Simplest for continuous m-dimensional instance space is Euclidean distance. n Simplest for m-dimensional binary instance space is Hamming distance (number of feature values that differ). n For text, cosine similarity of tf. idf weighted vectors is typically most effective. Prasad L 14 Vector. Classify 19
Illustration of 3 Nearest Neighbor for Text Vector Space Prasad L 14 Vector. Classify 20

Nearest Neighbor with Inverted Index n n Naively finding nearest neighbors requires a linear search through |D| documents in collection But determining k nearest neighbors is the same as determining the k best retrievals using the test document as a query to a database of training documents. Heuristics: Use standard vector space inverted index methods to find the k nearest neighbors. Testing Time: O(B|Vt|) where B is the average number of training documents in which a testdocument word appears. n Typically B << |D| Prasad L 14 Vector. Classify 21

k. NN: Discussion n n No feature selection necessary Scales well with large number of classes n n No training necessary n n n Actually: some data editing may be necessary. Classes can influence each other n n Don’t need to train n classifiers for n classes Small changes to one class can have ripple effect Scores can be hard to convert to probabilities May be more expensive at test time Prasad L 14 Vector. Classify 22
![k. NN vs. Naive Bayes : Bias/Variance tradeoff [Bias : Variance] : : Lack k. NN vs. Naive Bayes : Bias/Variance tradeoff [Bias : Variance] : : Lack](http://slidetodoc.com/presentation_image_h2/064c1444e4c88c2760f97d89ccd84252/image-23.jpg)
k. NN vs. Naive Bayes : Bias/Variance tradeoff [Bias : Variance] : : Lack of [expressiveness : robustness] n k. NN has high variance and low bias. n n NB has low variance and high bias. n n Infinite memory Decision surface has to be linear (hyperplane – see later) Consider asking a botanist: Is an object a tree? n Too much capacity/variance, low bias n n n Not enough capacity/variance, high bias n n n Botanist who memorizes Will always say “no” to new object (e. g. , different # of leaves) Lazy botanist Says “yes” if the object is green You want the middle ground (Example due to C. Burges) 23
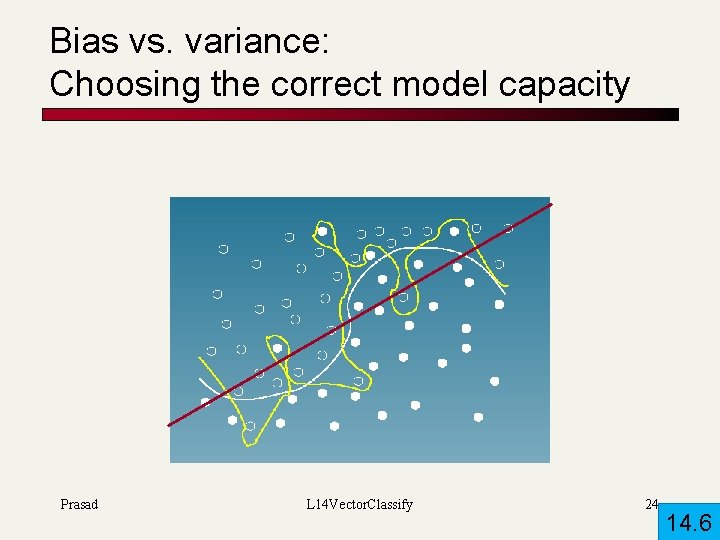
Bias vs. variance: Choosing the correct model capacity Prasad L 14 Vector. Classify 24 14. 6

Decision Boundaries Classification Prasad L 14 Vector. Classify 25

Binary Classification : Linear Classifier n Consider 2 class problems n n n Deciding between two classes, perhaps, government and non-government [one-versus-rest classification] How do we define (and find) the separating surface? How do we test which region a test doc is in? Prasad L 14 Vector. Classify 26

Separation by Hyperplanes n n A strong high-bias assumption is linear separability: n in 2 dimensions, can separate classes by a line n in higher dimensions, need hyperplanes Can find separating hyperplane by linear programming (or can iteratively fit solution via perceptron): n Prasad separator can be expressed as ax + by = c 27
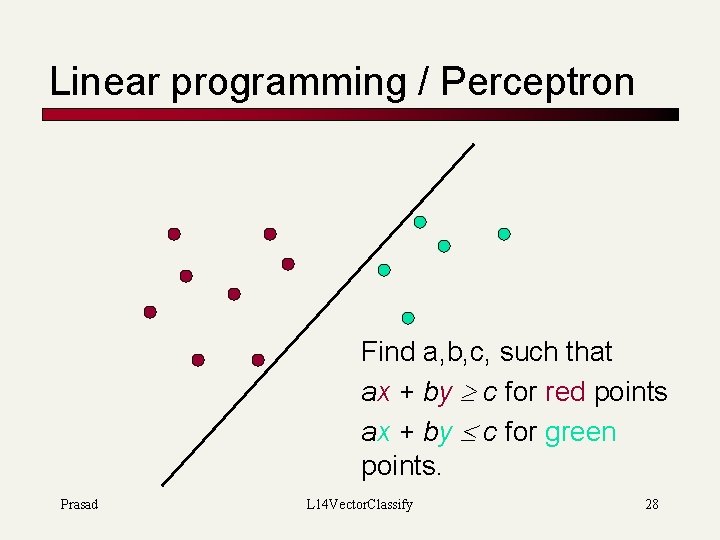
Linear programming / Perceptron Find a, b, c, such that ax + by c for red points ax + by c for green points. Prasad L 14 Vector. Classify 28
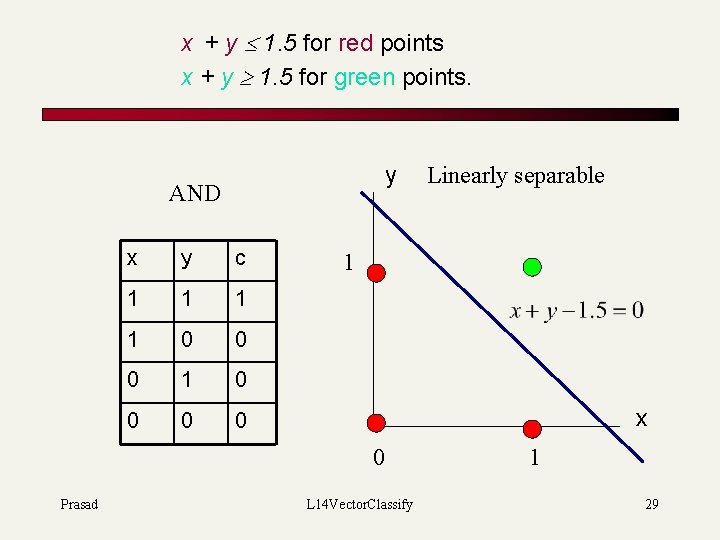
x + y 1. 5 for red points x + y 1. 5 for green points. y AND x y c 1 1 0 0 0 1 x 0 Prasad Linearly separable L 14 Vector. Classify 1 29
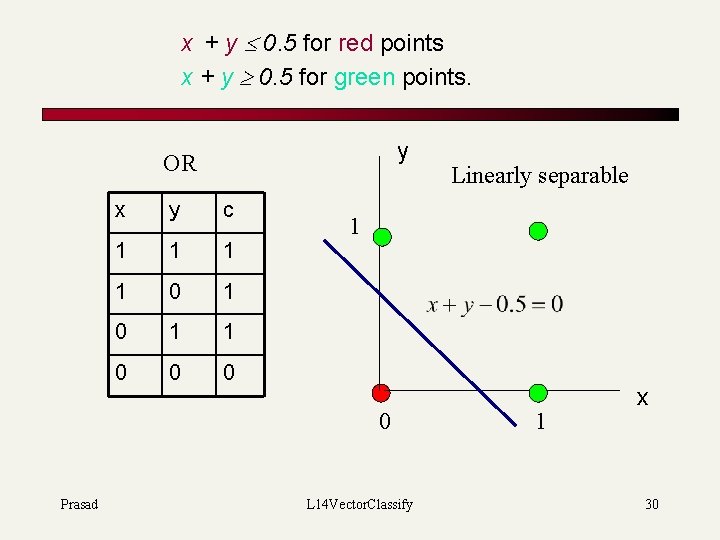
x + y 0. 5 for red points x + y 0. 5 for green points. y OR x y c 1 1 0 0 0 1 0 Prasad Linearly separable L 14 Vector. Classify 1 x 30
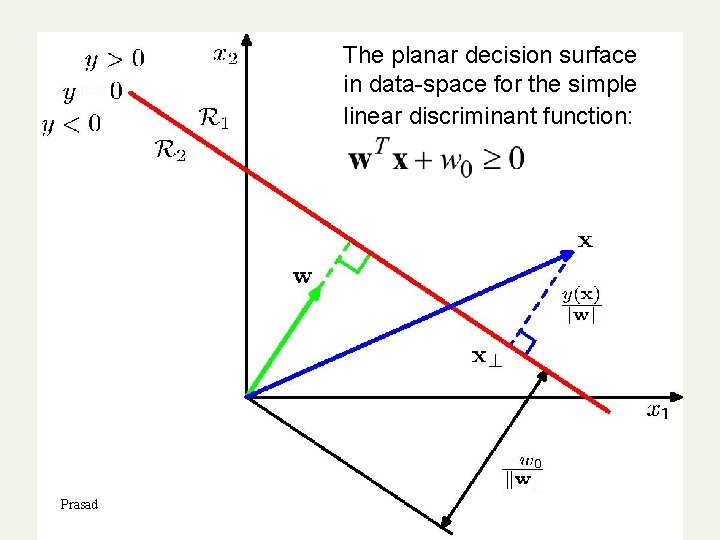
The planar decision surface in data-space for the simple linear discriminant function: Prasad 31
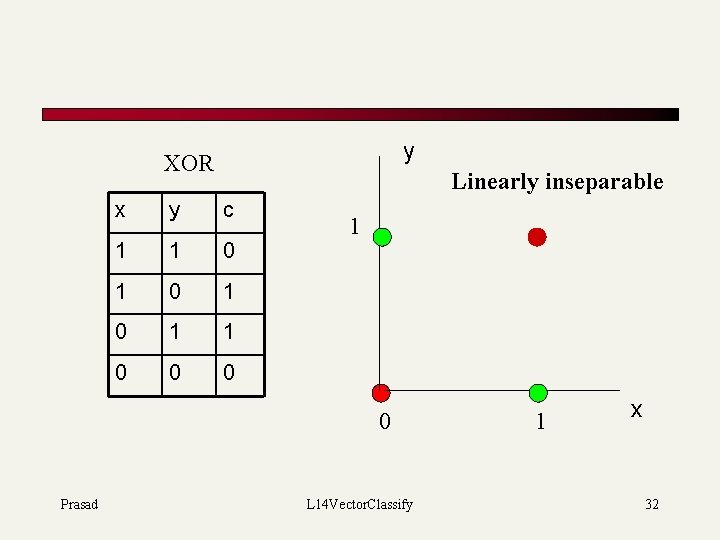
y XOR Linearly inseparable x y c 1 1 0 1 0 1 1 0 0 0 1 0 Prasad L 14 Vector. Classify 1 x 32
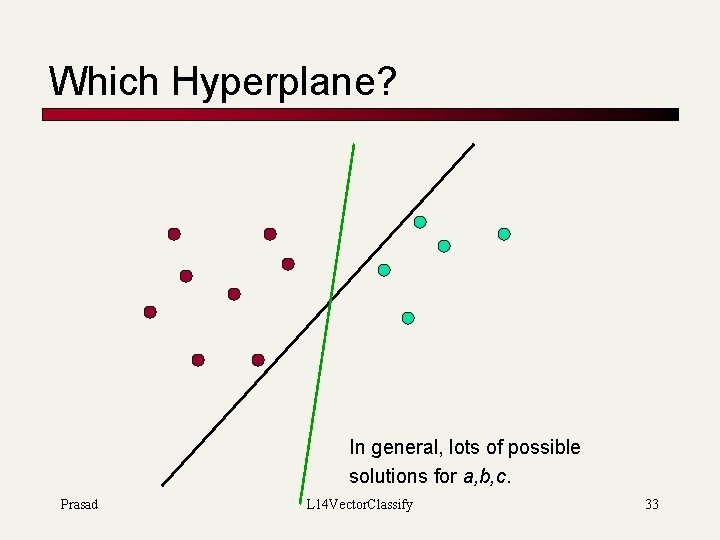
Which Hyperplane? In general, lots of possible solutions for a, b, c. Prasad L 14 Vector. Classify 33

Which Hyperplane? n n Lots of possible solutions for a, b, c. Some methods find a separating hyperplane, but not the optimal one [according to some criterion of expected goodness] n n E. g. , perceptron Which points should influence optimality? n n All points n Linear regression, Naïve Bayes Only “difficult points” close to decision boundary n Support vector machines 34

Linear Classifiers n Many common text classifiers are linear classifiers n Naïve Bayes n Perceptron n Rocchio n Logistic regression n Support vector machines (with linear kernel) n Linear regression n (Simple) perceptron neural networks Prasad L 14 Vector. Classify 35

Linear Classifiers n Despite this similarity, noticeable performance differences n n For separable problems, there are infinite number of separating hyperplanes. Which one do you choose? What to do for non-separable problems? Different training methods pick different hyperplanes Classifiers more powerful than linear often don’t perform better. Why? Prasad L 14 Vector. Classify 36

Naive Bayes is a linear classifier n n n Two-class Naive Bayes. We compute: Decide class C if the odds is greater than 1, i. e. , if the log odds is greater than 0. So decision boundary is hyperplane: 37
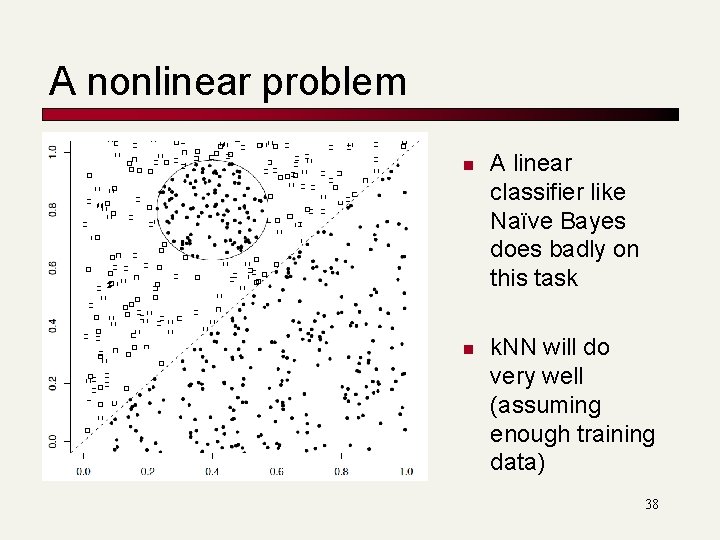
A nonlinear problem n n A linear classifier like Naïve Bayes does badly on this task k. NN will do very well (assuming enough training data) 38

High Dimensional Data n Pictures like the on the right are absolutely misleading! n n Documents are zero along almost all axes Most document pairs are very far apart (i. e. , not strictly orthogonal, but only share very common words and a few scattered others) In classification terms: virtually all document sets are separable, for most classification This is partly why linear classifiers are quite successful in this domain Prasad L 14 Vector. Classify 39

More Than Two Classes n Any-of or multivalue classification n n Classes are independent of each other. A document can belong to 0, 1, or >1 classes. Decompose into n binary problems Quite common for documents One-of or multinomial or polytomous classification n Prasad Classes are mutually exclusive. Each document belongs to exactly one class E. g. , digit recognition is polytomous classification n Digits are mutually exclusive 40 14. 5

Set of Binary Classifiers: Any of n n Build a separator between each class and its complementary set (docs from all other classes). Given test doc, evaluate it for membership in each class. Apply decision criterion of classifiers independently Done n Prasad Sometimes you could do better by considering dependencies between categories L 14 Vector. Classify 41

Set of Binary Classifiers: One of n n n Build a separator between each class and its complementary set (docs from all other classes). Given test doc, evaluate it for membership in each class. Assign document to class with: n n maximum score maximum confidence maximum probability Why different from multiclass/ any of classification? Prasad L 14 Vector. Classify ? ? ? 42

Classification using Centroids Prasad L 14 Vector. Classify 43

Relevance feedback: Basic idea §The user issues a (short, simple) query. §The search engine returns a set of documents. §User marks some docs as relevant, some as nonrelevant. §Search engine computes a new representation of the information need – should be better than the initial query. §Search engine runs new query and returns new results. §New results have (hopefully) better recall. 44
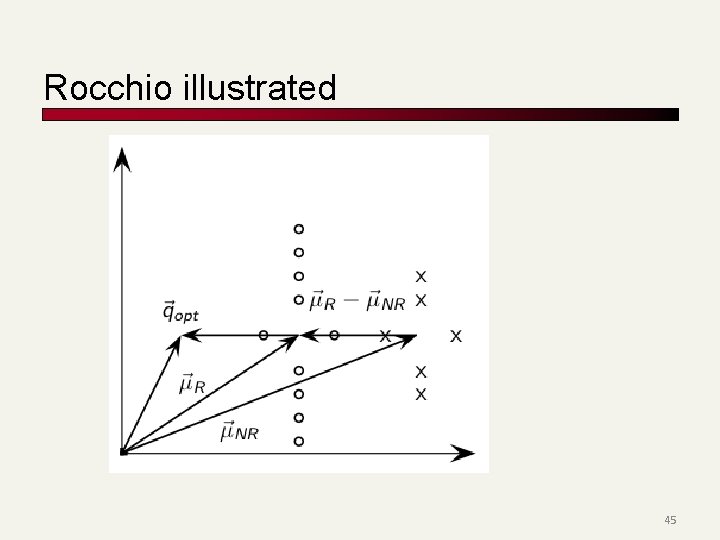
Rocchio illustrated 45

Using Rocchio for text classification n Relevance feedback methods can be adapted for text categorization n n 2 -classification (Relevant vs. nonrelevant documents) Use standard TF/IDF weighted vectors to represent text documents For each category, compute a prototype vector by summing the vectors of the training documents in the category. n Prototype = centroid of members of class Assign test documents to the category with the closest prototype vector based on cosine similarity. Prasad L 14 Vector. Classify 46 14. 2
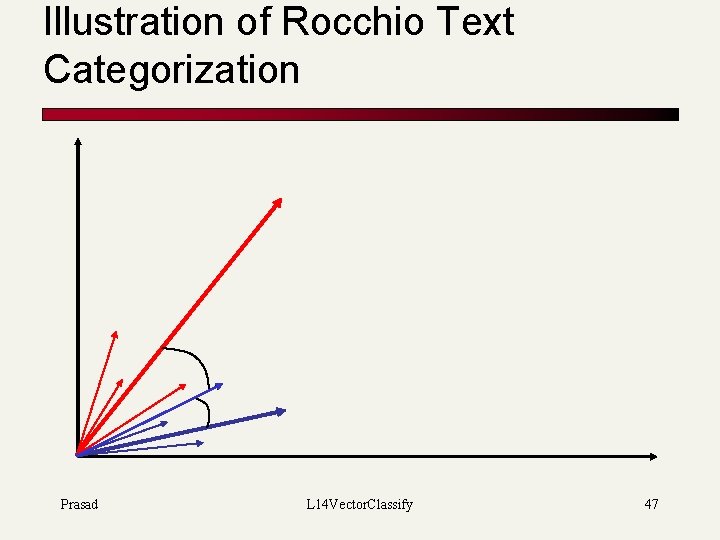
Illustration of Rocchio Text Categorization Prasad L 14 Vector. Classify 47

Definition of centroid n n Where Dc is the set of all documents that belong to class c and v(d) is the vector space representation of d. Note that centroid will in general not be a unit vector even when the inputs are unit vectors. 48

Rocchio Properties n n Forms a simple generalization of the examples in each class (a prototype). Prototype vector does not need to be averaged or otherwise normalized for length since cosine similarity is insensitive to vector length. Classification is based on similarity to class prototypes. Does not guarantee classifications are consistent with the given training data. Prasad L 14 Vector. Classify 49
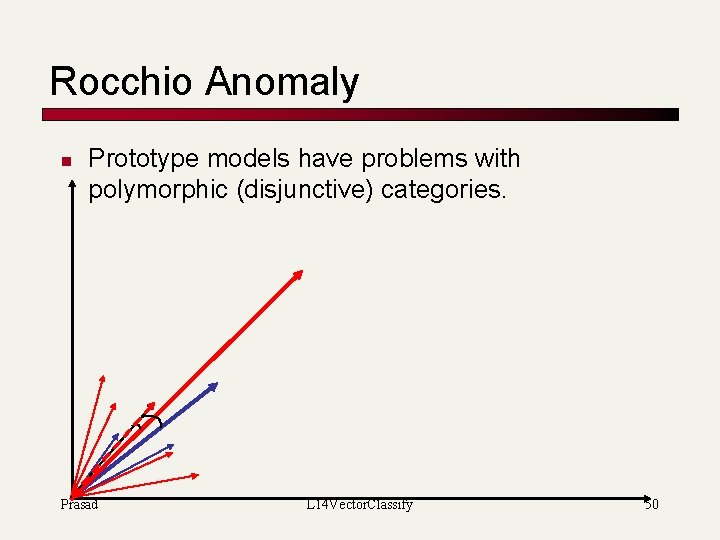
Rocchio Anomaly n Prototype models have problems with polymorphic (disjunctive) categories. Prasad L 14 Vector. Classify 50
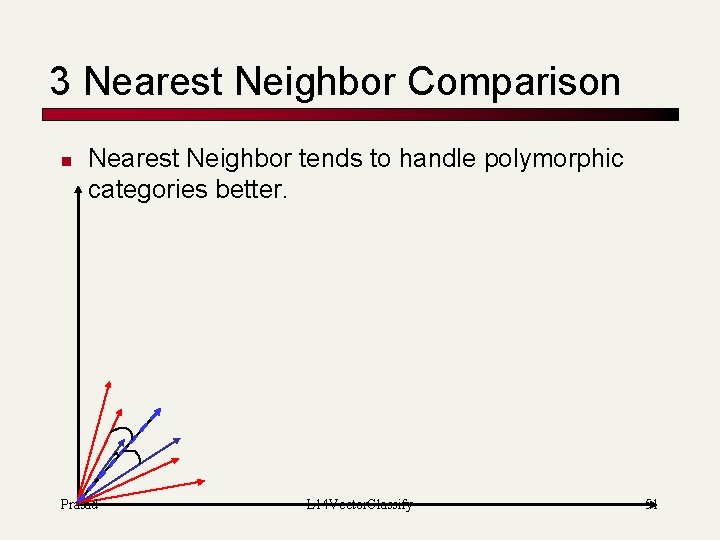
3 Nearest Neighbor Comparison n Nearest Neighbor tends to handle polymorphic categories better. Prasad L 14 Vector. Classify 51
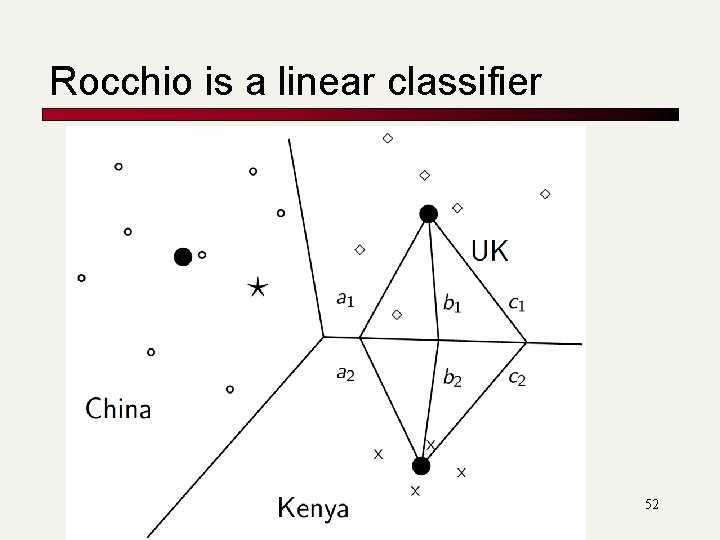
Rocchio is a linear classifier 52

Two-class Rocchio as a linear classifier n Line or hyperplane defined by: n For Rocchio, set: 53

Rocchio classification n n Rocchio forms a simple representation for each class: the centroid/prototype Classification is based on similarity to / distance from the prototype/centroid It does not guarantee that classifications are consistent with the given training data It is little used outside text classification, but has been used quite effectively for text classification Again, cheap to train and test documents 54
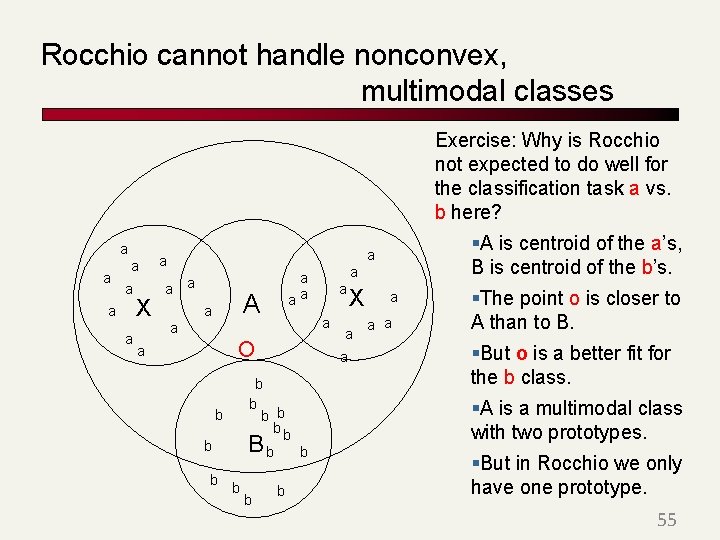
Rocchio cannot handle nonconvex, multimodal classes Exercise: Why is Rocchio not expected to do well for the classification task a vs. b here? a a a X a §A is centroid of the a’s, B is centroid of the b’s. a a A a O B b b b X a a b b bb b a a a aa a §The point o is closer to A than to B. §But o is a better fit for the b class. §A is a multimodal class with two prototypes. §But in Rocchio we only have one prototype. 55

SKIP WHAT FOLLOWS Prasad L 14 Vector. Classify 56

Decision Tree Classification n n n Tree with internal nodes labeled by terms Branches are labeled by tests on the weight that the term has Leaves are labeled by categories Classifier categorizes document by descending tree following tests to leaf The label of the leaf node is then assigned to the document Most decision trees are binary trees (advantageous; may require extra internal nodes) DT make good use of a few high-leverage features 57
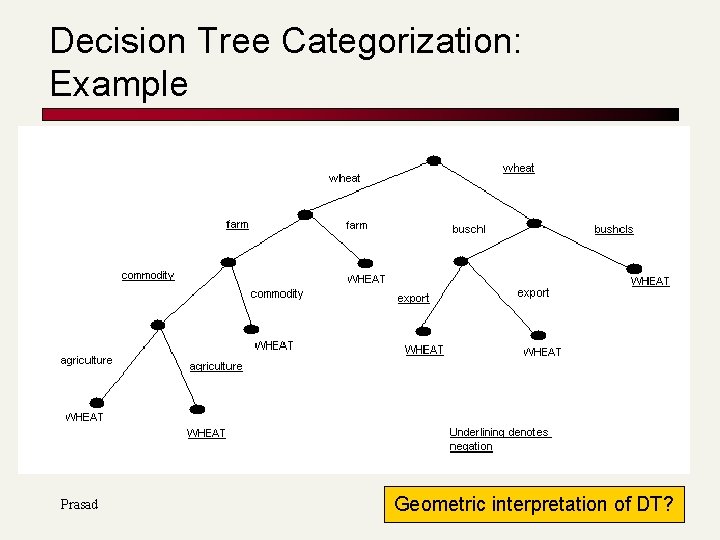
Decision Tree Categorization: Example Prasad Geometric interpretation of DT?
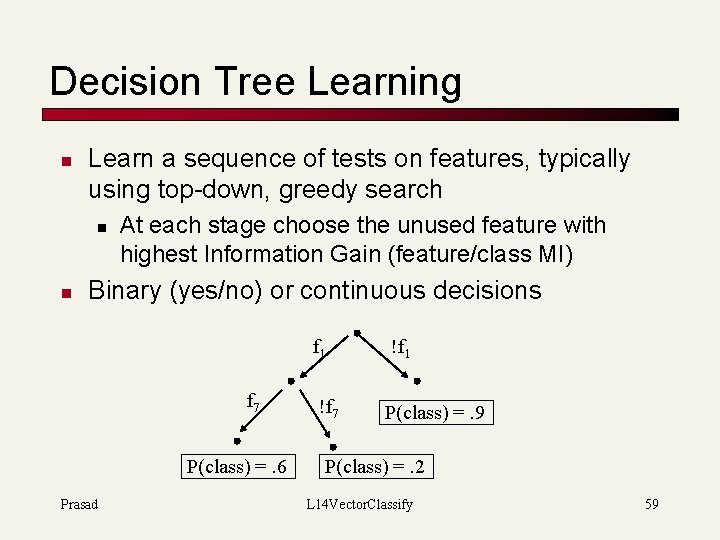
Decision Tree Learning n Learn a sequence of tests on features, typically using top-down, greedy search n n At each stage choose the unused feature with highest Information Gain (feature/class MI) Binary (yes/no) or continuous decisions f 7 P(class) =. 6 Prasad f 1 !f 7 P(class) =. 9 P(class) =. 2 L 14 Vector. Classify 59

Entropy Calculations If we have a set with k different values in it, we can calculate the entropy as follows: Where P(valuei) is the probability of getting the ith value when randomly selecting one from the set. So, for the set R = {a, a, a, b, b, b} Prasad a-values b-values 60
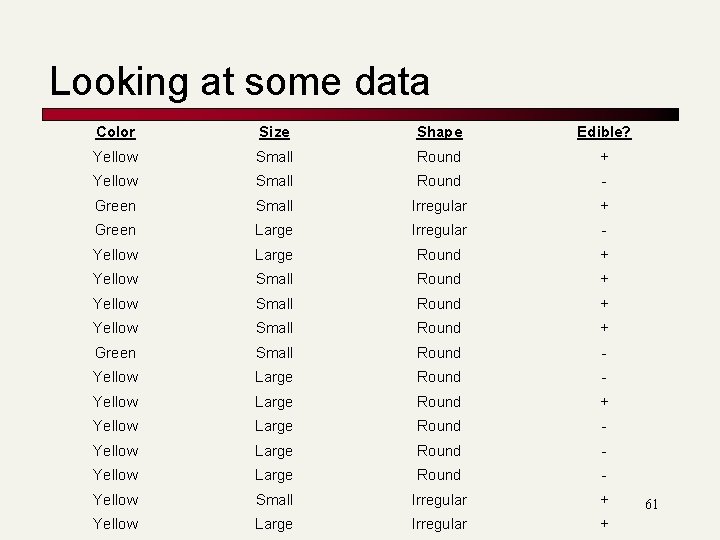
Looking at some data Color Size Shape Edible? Yellow Small Round + Yellow Small Round - Green Small Irregular + Green Large Irregular - Yellow Large Round + Yellow Small Round + Green Small Round - Yellow Large Round + Yellow Large Round - Yellow Small Irregular + Yellow Large Irregular + 61

Entropy for our data set n n n 16 instances: 9 positive, 7 negative. This equals: 0. 9836 This makes sense – it’s almost a 50/50 split; so, the entropy should be close to 1. Prasad L 14 Vector. Classify 62
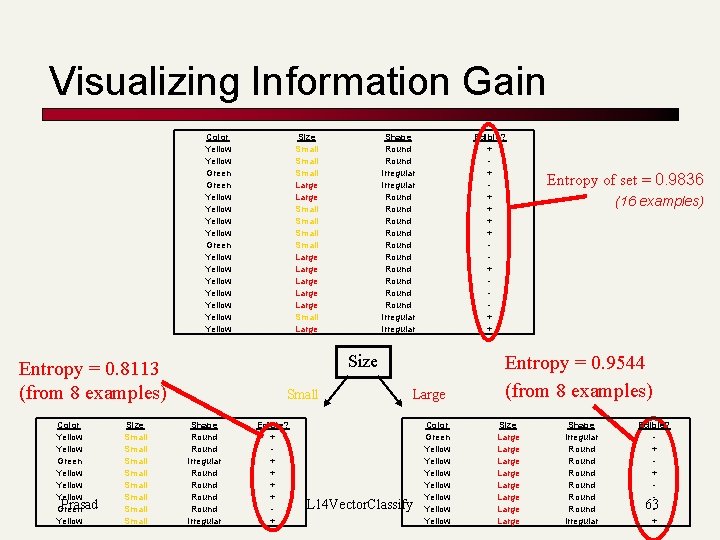
Visualizing Information Gain Color Yellow Green Yellow Yellow Yellow Size Small Small Shape Round Irregular Round Round Round Irregular Edible? + + + + + Size Entropy = 0. 8113 (from 8 examples) Color Yellow Green Yellow Prasad Green Yellow Size Small Small Large Large Small Shape Round Irregular Round Irregular Edible? + + + Large L 14 Vector. Classify Color Green Yellow Yellow Entropy of set = 0. 9836 (16 examples) Entropy = 0. 9544 (from 8 examples) Size Large Large Shape Irregular Round Round Irregular Edible? + + 63+
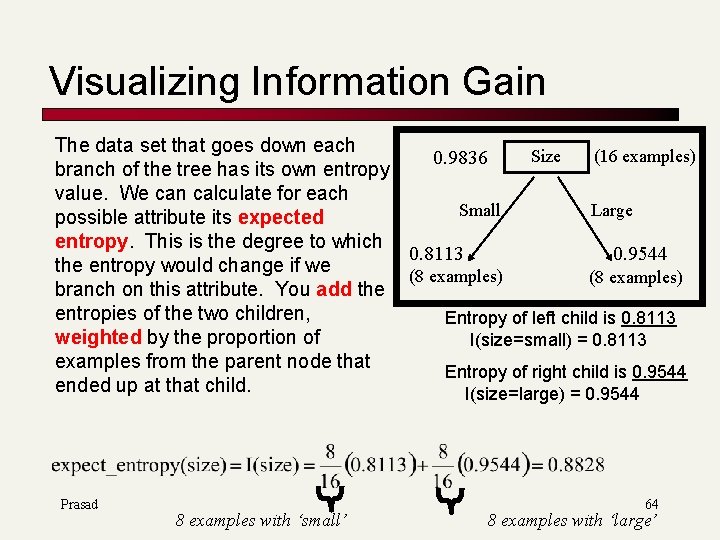
Visualizing Information Gain The data set that goes down each Size (16 examples) 0. 9836 branch of the tree has its own entropy value. We can calculate for each Small Large possible attribute its expected entropy. This is the degree to which 0. 8113 0. 9544 the entropy would change if we (8 examples) branch on this attribute. You add the entropies of the two children, Entropy of left child is 0. 8113 weighted by the proportion of I(size=small) = 0. 8113 examples from the parent node that Entropy of right child is 0. 9544 ended up at that child. I(size=large) = 0. 9544 Prasad 8 examples with ‘small’ 64 8 examples with ‘large’

G(attrib) = I(parent) – I(attrib) We want to calculate the information gain (or entropy reduction). This is the reduction in ‘uncertainty’ when choosing our first branch as ‘size’. We will represent information gain as “G. ” G(size) = I(parent) – I(size) G(size) = 0. 9836 – 0. 8828 G(size) = 0. 1008 Entropy of all data at parent node = I(parent) = 0. 9836 Child’s expected entropy for ‘size’ split = I(size) = 0. 8828 So, we have gained 0. 1008 bits of information about the dataset by choosing ‘size’ as the first branch of our decision tree. Prasad L 14 Vector. Classify 65

Decision Tree Learning n Fully grown trees tend to have decision rules that are overly specific and therefore unable to categorize documents well n n Therefore, pruning or early stopping methods for Decision Trees are normally a standard part of classification packages Use of small number of features is potentially bad in text categorization, but in practice decision trees do well for some text classification tasks Decision trees are easily interpreted by humans – compared to probabilistic methods like Naive Bayes Decision Trees are normally regarded as a symbolic machine learning algorithm, though they can be used probabilistically Prasad L 14 Vector. Classify 66
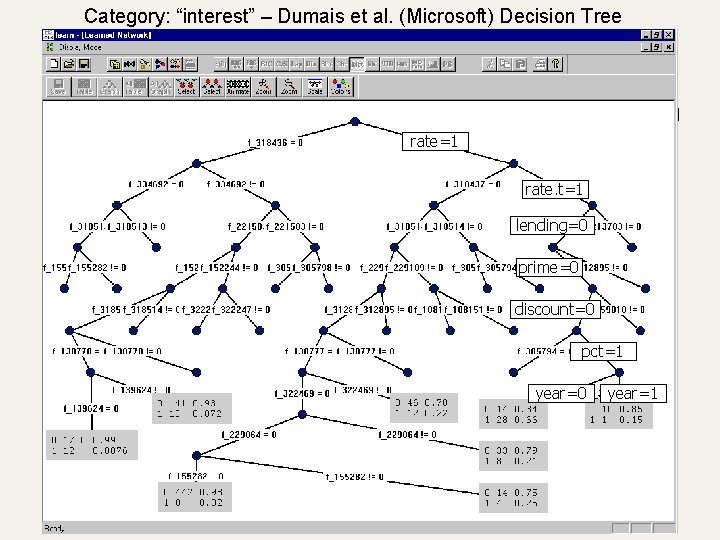
Category: “interest” – Dumais et al. (Microsoft) Decision Tree rate=1 rate. t=1 lending=0 prime=0 discount=0 pct=1 year=0 year=1 67

Summary: Representation of Text Categorization Attributes n n Representations of text are usually very high dimensional (one feature for each word) High-bias algorithms that prevent overfitting in high-dimensional space generally work best For most text categorization tasks, there are many relevant features and many irrelevant ones Methods that combine evidence from many or all features (e. g. naive Bayes, k. NN, neural-nets) often tend to work better than ones that try to isolate just a few relevant features (standard decision-tree or rule induction)* Prasad *Although one can compensate by using many rules

Which classifier do I use for a given text classification problem? n Is there a learning method that is optimal for all text classification problems? n n No, because of bias-variance tradeoff. Factors to take into account: n n How much training data is available? How simple/complex is the problem? (linear vs. nonlinear decision boundary) How noisy is the problem? How stable is the problem over time? n For an unstable problem, it’s better to use a simple and robust classifier. 69
- Slides: 69