Vector Resolution and Projectile Motion Honors Physics Vector

Vector Resolution and Projectile Motion Honors Physics

Vector Terminology n The sum of 2 or more vectors is called the resultant (R). q n n A single vector that can replace concurrent vectors Any vector can be described as having both x and y components in a coordinate system. The process of breaking a single vector into its x and y components is called vector resolution.

More Vector Terminology n n Vectors are said to be in equilibrium if their sum is equal to zero. A single vector that can be added to others to produce equilibrium is call the equilibrant (E). q Equal to the resultant in magnitude but opposite in direction. E+R=0 E=-R E=5 N R=5 N at 180 ° at 0°

Using the Graphical Method of Vector Addition: n n Vectors are drawn to scale and the resultant is determined using a ruler and protractor. Vectors are added by drawing the tail of the second vector at the head of the first (tip to tail method). q n The order of addition does not matter. The resultant is always drawn from the tail of the first to the head of the last vector.

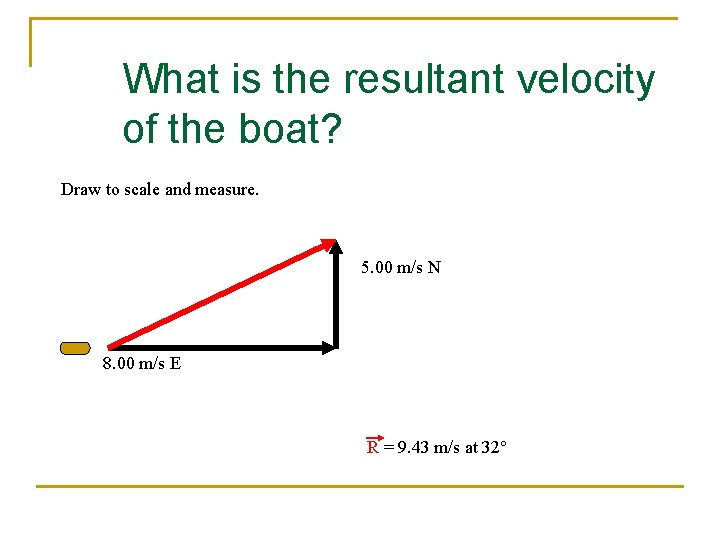
Example Problem: Motion in 2 Dimensions n A boat heads east at 8. 00 m/s across a river flowing north at 5. 00 m/s. q What is the resultant velocity of the boat?

What is the resultant velocity of the boat? Draw to scale and measure. 5. 00 m/s N 8. 00 m/s E R = 9. 43 m/s at 32°

n n n Solving Vector Problems using the Component Method Each vector is replaced by 2 perpendicular vectors called components. Add the x-components and the y-components to find the x- and y-components of the resultant. Use the Pythagorean theorem and the tangent function to find the magnitude and direction of the resultant.

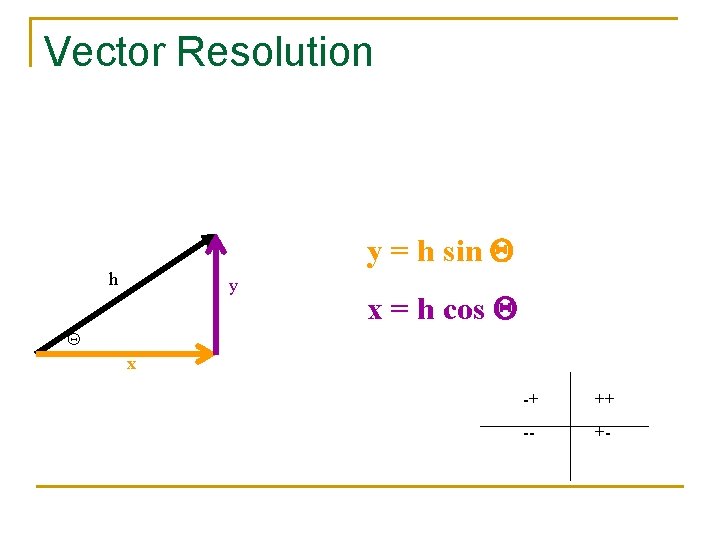
Vector Resolution y = h sin h y x = h cos x -+ ++ -- +-

What is projectile? Projectile -Any object which projected by some means and continues to move due to its own inertia (mass).

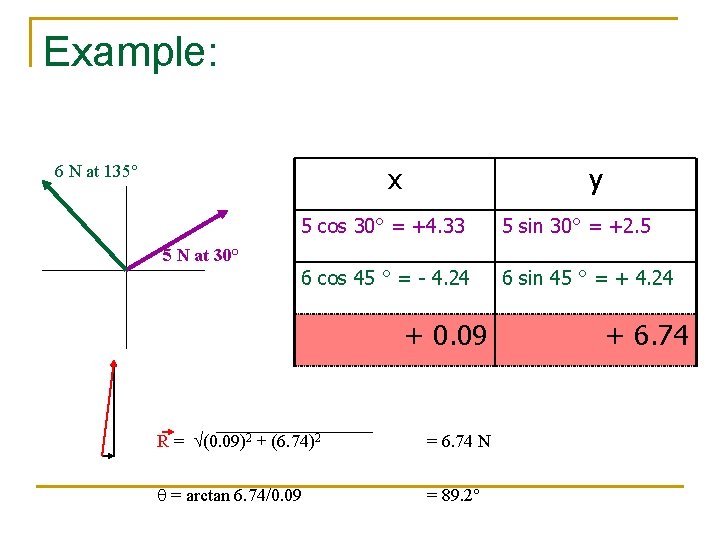
Example: 6 N at 135° x y 5 cos 30° = +4. 33 5 sin 30° = +2. 5 6 cos 45 ° = - 4. 24 6 sin 45 ° = + 4. 24 5 N at 30° + 0. 09 R = (0. 09)2 + (6. 74)2 = 6. 74 N = arctan 6. 74/0. 09 = 89. 2° + 6. 74

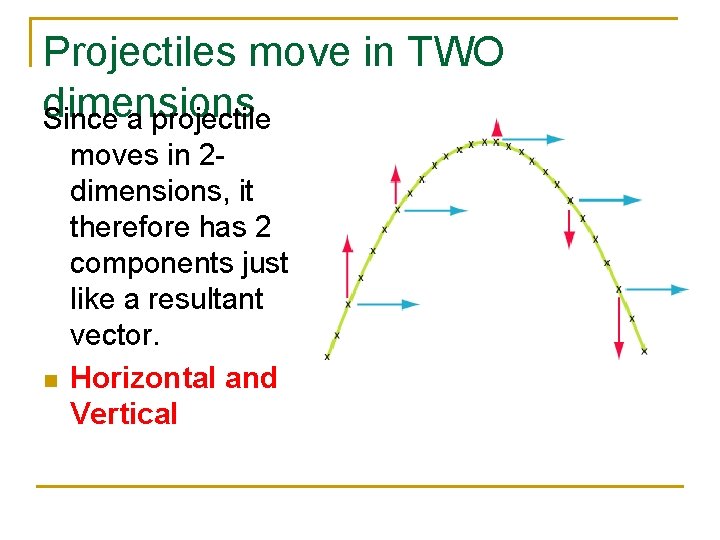
Projectiles move in TWO dimensions Since a projectile n moves in 2 dimensions, it therefore has 2 components just like a resultant vector. Horizontal and Vertical

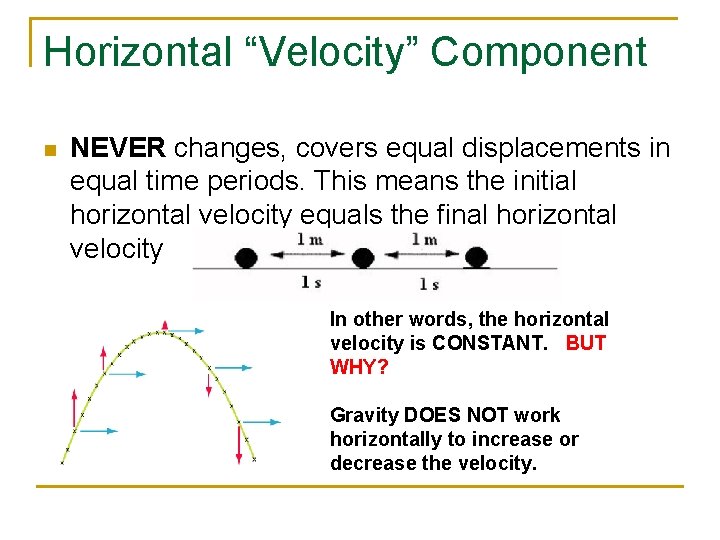
Horizontal “Velocity” Component n NEVER changes, covers equal displacements in equal time periods. This means the initial horizontal velocity equals the final horizontal velocity In other words, the horizontal velocity is CONSTANT. BUT WHY? Gravity DOES NOT work horizontally to increase or decrease the velocity.

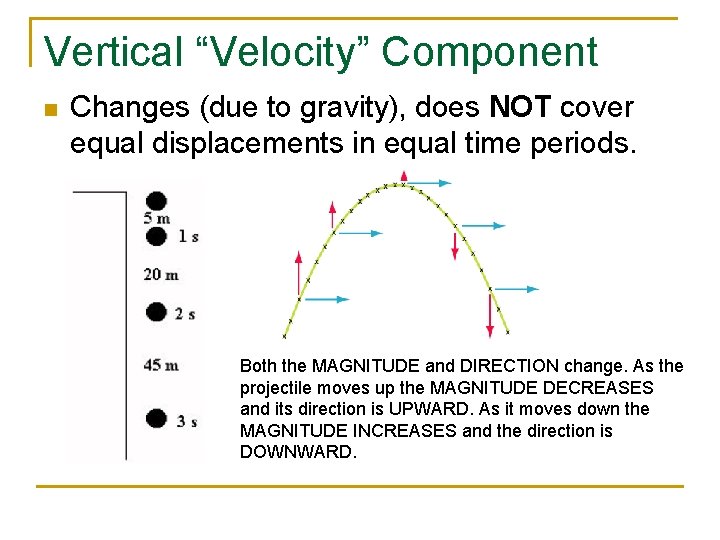
Vertical “Velocity” Component n Changes (due to gravity), does NOT cover equal displacements in equal time periods. Both the MAGNITUDE and DIRECTION change. As the projectile moves up the MAGNITUDE DECREASES and its direction is UPWARD. As it moves down the MAGNITUDE INCREASES and the direction is DOWNWARD.

Combining the Components Together, these components produce what is called a trajectory or path. This path is parabolic in nature. Component Magnitude Direction Horizontal Constant Vertical Changes

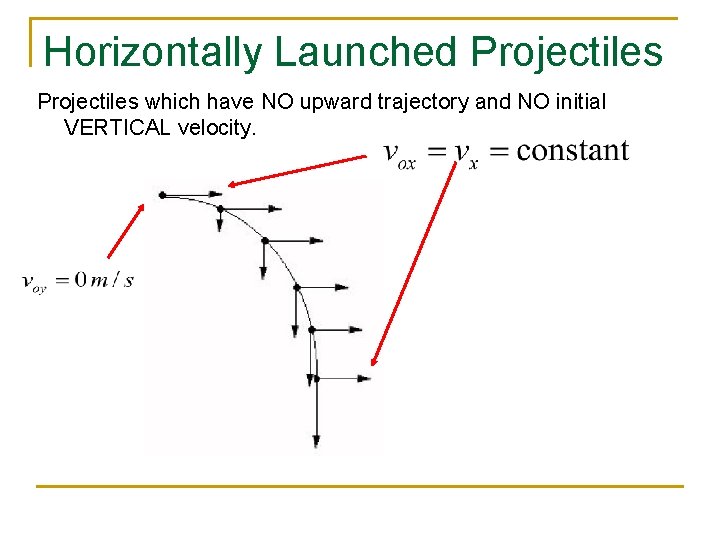
Horizontally Launched Projectiles which have NO upward trajectory and NO initial VERTICAL velocity.

Horizontally Launched Projectiles To analyze a projectile in 2 dimensions we need 2 equations. One for the “x” direction and one for the “y” direction. And for this we use kinematic #2. Remember, the velocity is CONSTANT horizontally, so that means the acceleration is ZERO! Remember that since the projectile is launched horizontally, the INITIAL VERTICAL VELOCITY is equal to ZERO.

Horizontally Launched Projectiles Example: A plane traveling with a horizontal velocity of 100 m/s is 500 m above the ground. At some point the pilot decides to drop some supplies to designated target below. (a) How long is the drop in the air? (b) How far away from point where it was launched will it land? What do I know? What I want to know? vox=100 m/s t=? x=? y = 500 m voy= 0 m/s g = -9. 8 m/s/s 1010 m 10. 1 seconds

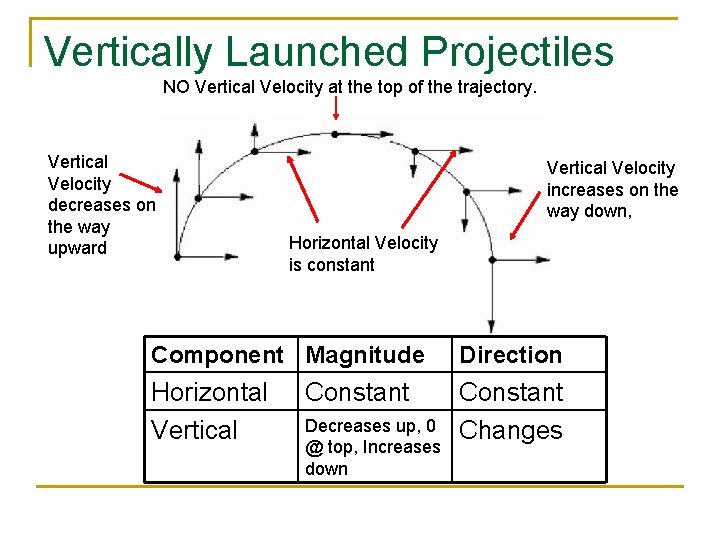
Vertically Launched Projectiles NO Vertical Velocity at the top of the trajectory. Vertical Velocity decreases on the way upward Vertical Velocity increases on the way down, Horizontal Velocity is constant Component Magnitude Direction Horizontal Vertical Constant Changes Constant Decreases up, 0 @ top, Increases down

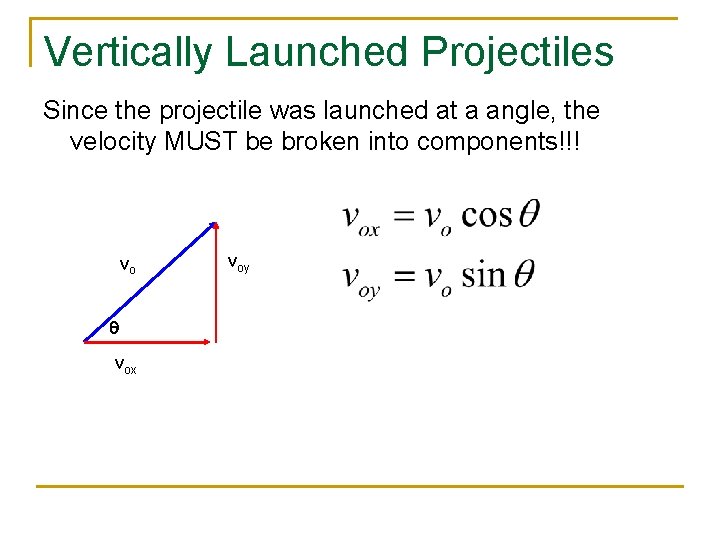
Vertically Launched Projectiles Since the projectile was launched at a angle, the velocity MUST be broken into components!!! vo q vox voy

Vertically Launched Projectiles There are several things you must consider when doing these types of projectiles besides using components. If it begins and ends at ground level, the “y” displacement is ZERO: y = 0

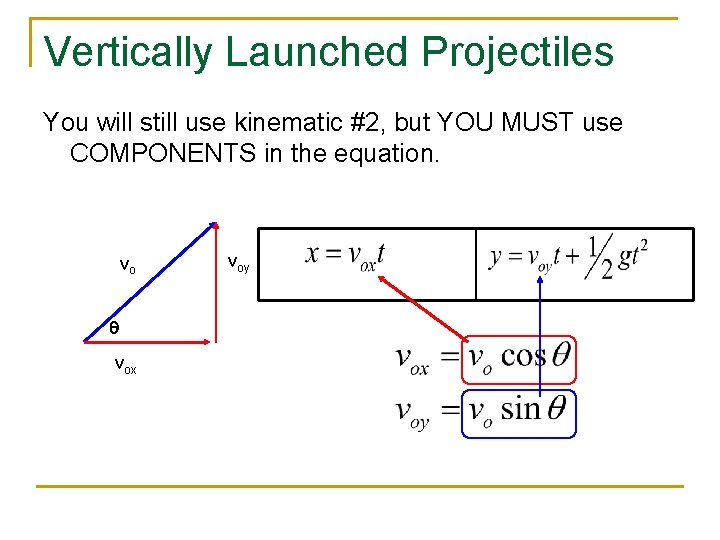
Vertically Launched Projectiles You will still use kinematic #2, but YOU MUST use COMPONENTS in the equation. vo q vox voy

Example A place kicker kicks a football with a velocity of 20. 0 m/s and at an angle of 53 degrees. (a) How long is the ball in the air? (b) How far away does it land? (c) How high does it travel? /s 0 0. v 2 = o q = 53 m

Example A place kicker kicks a football with a velocity of 20. 0 m/s and at an angle of 53 degrees. (a) How long is the ball in the air? 3. 26 s What I know What I want to know vox=12. 04 m/s t=? voy=15. 97 m/s x=? y=0 ymax=? g = - 9. 8 m/s/s

Example A place kicker kicks a football with a velocity of 20. 0 m/s and at an angle of 53 degrees. (b) How far away does it land? What I know What I want to know vox=12. 04 m/s t = 3. 26 s voy=15. 97 m/s x=? y=0 ymax=? g = - 9. 8 m/s/s 39. 24 m

Example A place kicker kicks a football with a velocity of 20. 0 m/s and at an angle of 53 degrees. (c) How high does it travel? What I know What I want to know vox=12. 04 m/s t = 3. 26 s voy=15. 97 m/s x = 39. 24 m y=0 ymax=? g = - 9. 8 m/s/s CUT YOUR TIME IN HALF! 13. 01 m