Vector Refresher Part 4 Vector Cross Product Definition

Vector Refresher Part 4 • Vector Cross Product Definition • Right Hand Rule • Cross Product Calculation • Properties of the Cross Product

Cross Product • The cross product is another method used to multiply vectors

Cross Product • The cross product is another method used to multiply vectors • Yields a vector result

Cross Product • The cross product is another method used to multiply vectors • Yields a vector result • This vector is orthogonal to both vectors used in the calculation

Symbolism • The cross product is symbolized with an x between 2 vectors

Symbolism • The cross product is symbolized with an x between 2 vectors • The following is stated “Vector A crossed with vector B. ”

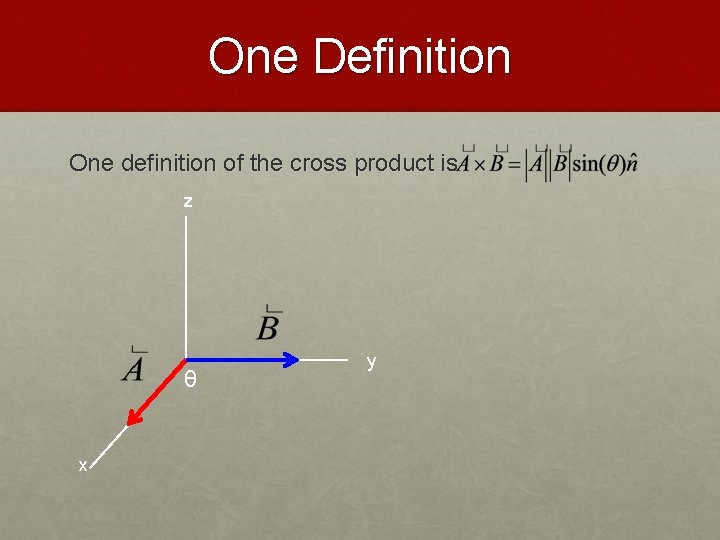
One Definition One definition of the cross product is

One Definition One definition of the cross product is z θ x y

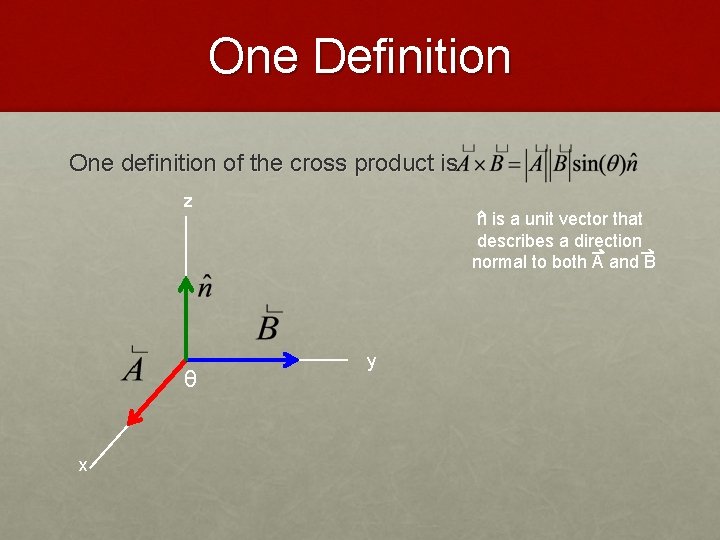
One Definition One definition of the cross product is z θ x n is a unit vector that describes a direction normal to both A and B y

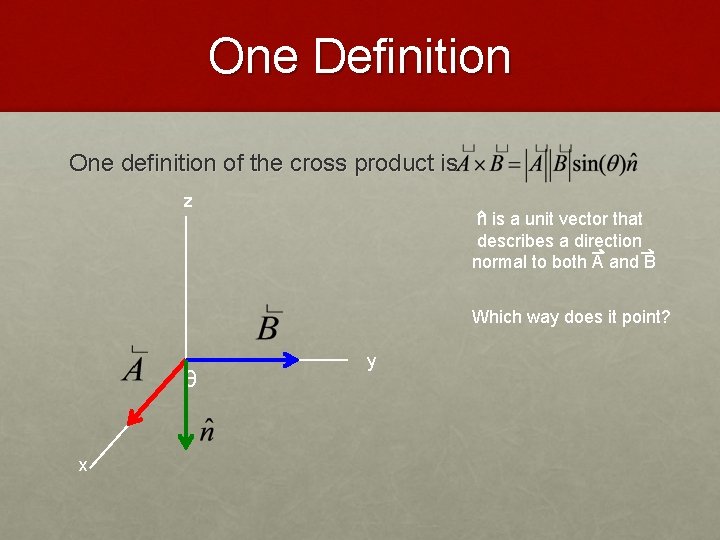
One Definition One definition of the cross product is z n is a unit vector that describes a direction normal to both A and B Which way does it point? θ x y

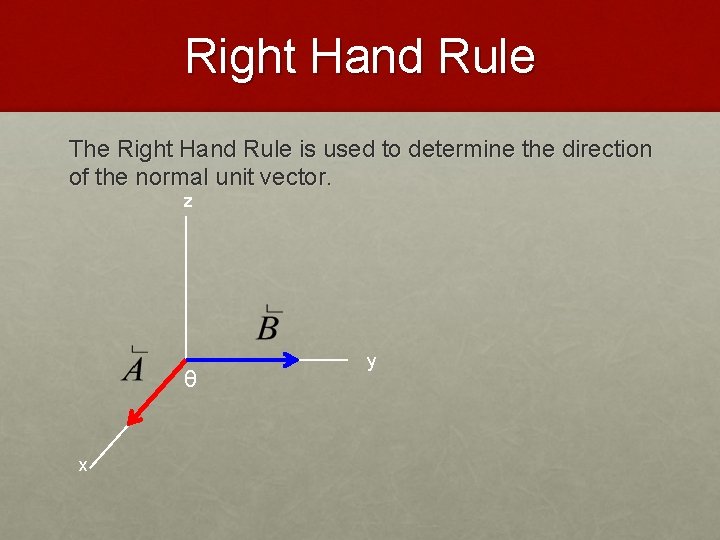
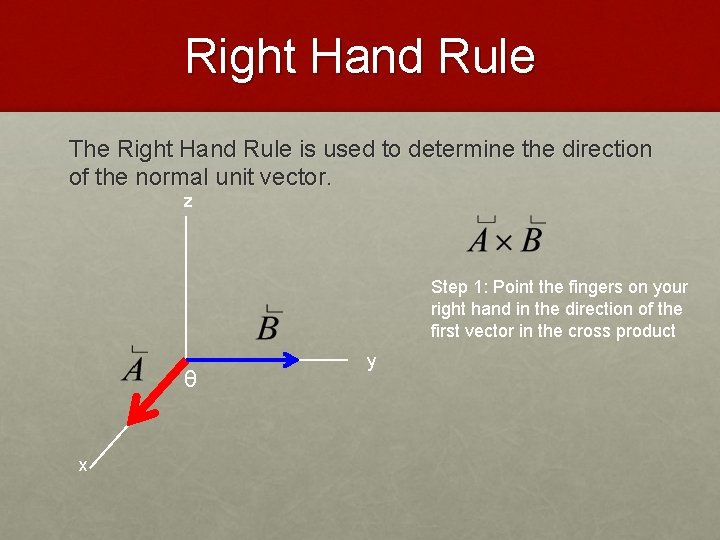
Right Hand Rule The Right Hand Rule is used to determine the direction of the normal unit vector. z θ x y

Right Hand Rule The Right Hand Rule is used to determine the direction of the normal unit vector. z θ x y

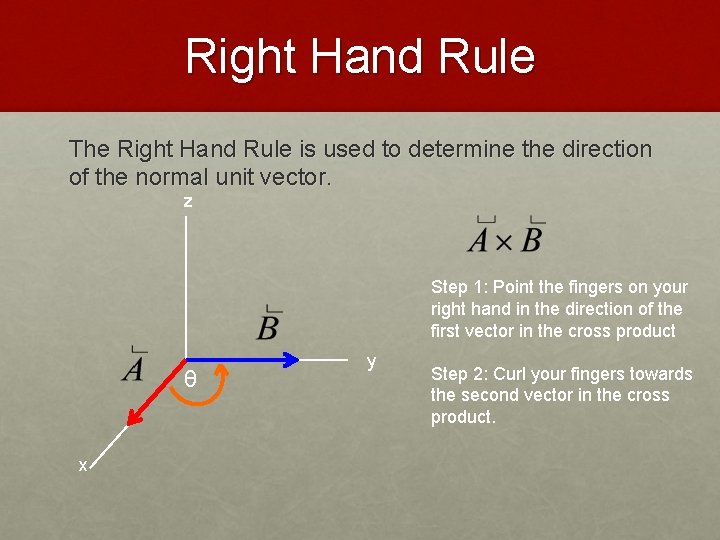
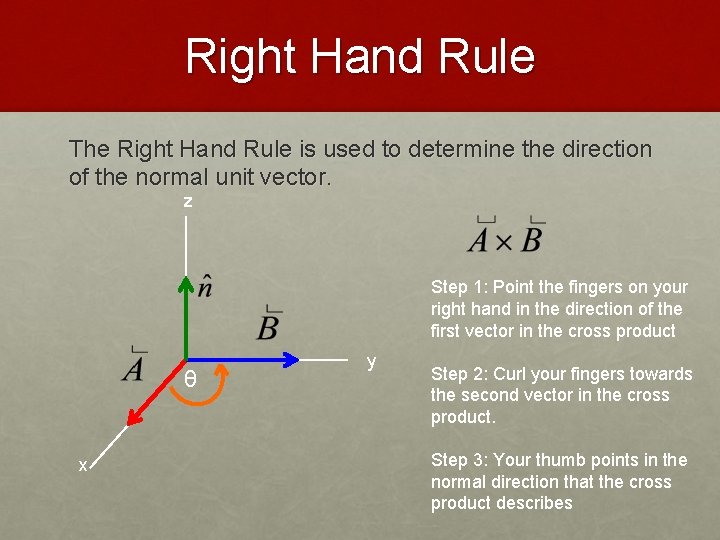
Right Hand Rule The Right Hand Rule is used to determine the direction of the normal unit vector. z Step 1: Point the fingers on your right hand in the direction of the first vector in the cross product θ x y

Right Hand Rule The Right Hand Rule is used to determine the direction of the normal unit vector. z Step 1: Point the fingers on your right hand in the direction of the first vector in the cross product θ x y Step 2: Curl your fingers towards the second vector in the cross product.

Right Hand Rule The Right Hand Rule is used to determine the direction of the normal unit vector. z Step 1: Point the fingers on your right hand in the direction of the first vector in the cross product θ x y Step 2: Curl your fingers towards the second vector in the cross product. Step 3: Your thumb points in the normal direction that the cross product describes

One Definition This definition of the cross product is of limited usefulness because you need to know the normal direction. z θ x y

One Definition This definition of the cross product is of limited usefulness because you need to know the normal direction. z θ x y You can use this to find the angle between the 2 vectors, but the dot product is an easier way to do this

Another De. Finition The cross product can also be evaluated as the determinant of a 3 x 3 matrix

Another De. Finition The cross product can also be evaluated as the determinant of a 3 x 3 matrix

Another De. Finition The cross product can also be evaluated as the determinant of a 3 x 3 matrix

Another De. Finition The cross product can also be evaluated as the determinant of a 3 x 3 matrix

Another De. Finition The cross product can also be evaluated as the determinant of a 3 x 3 matrix

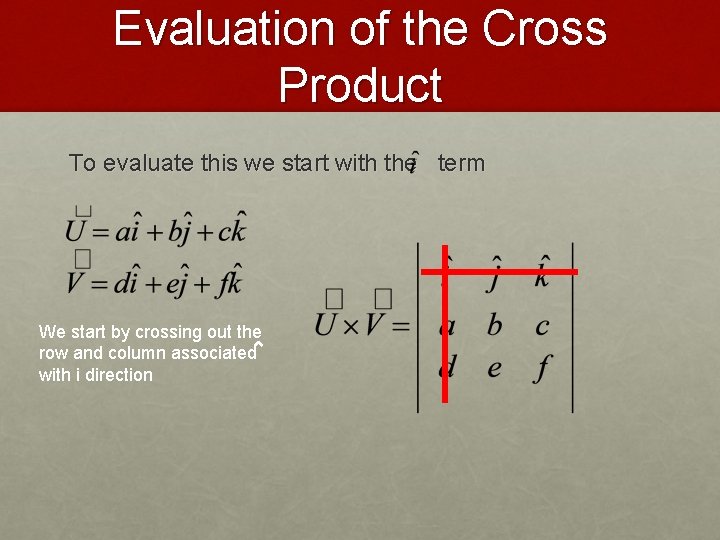
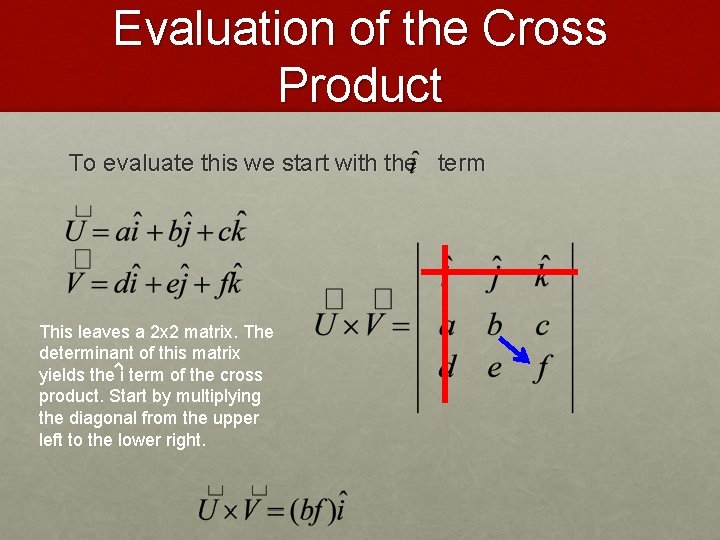
Evaluation of the Cross Product To evaluate this we start with the term We start by crossing out the row and column associated with i direction

Evaluation of the Cross Product To evaluate this we start with the term This leaves a 2 x 2 matrix. The determinant of this matrix yields the i term of the cross product

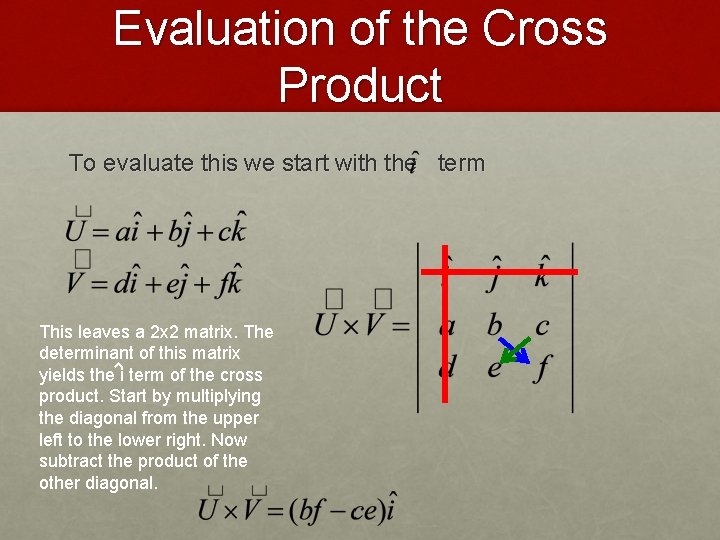
Evaluation of the Cross Product To evaluate this we start with the term This leaves a 2 x 2 matrix. The determinant of this matrix yields the i term of the cross product. Start by multiplying the diagonal from the upper left to the lower right.

Evaluation of the Cross Product To evaluate this we start with the term This leaves a 2 x 2 matrix. The determinant of this matrix yields the i term of the cross product. Start by multiplying the diagonal from the upper left to the lower right. Now subtract the product of the other diagonal.

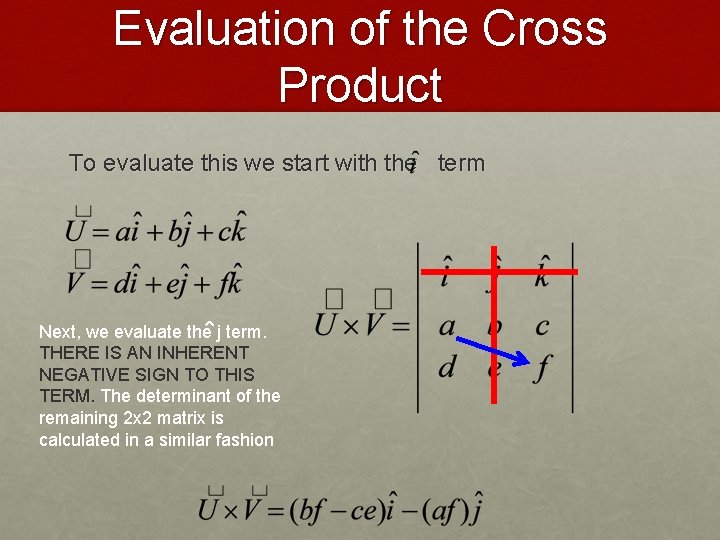
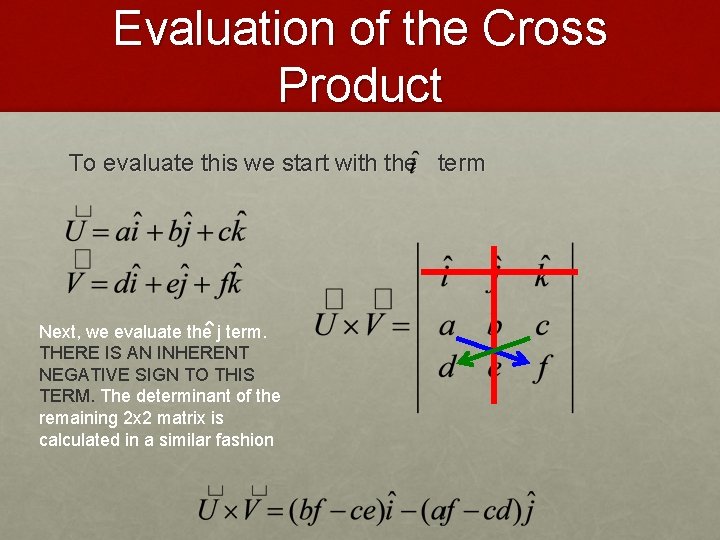
Evaluation of the Cross Product To evaluate this we start with the term Next, we evaluate the j term. THERE IS AN INHERENT NEGATIVE SIGN TO THIS TERM

Evaluation of the Cross Product To evaluate this we start with the term Next, we evaluate the j term. THERE IS AN INHERENT NEGATIVE SIGN TO THIS TERM. The determinant of the remaining 2 x 2 matrix is calculated in a similar fashion

Evaluation of the Cross Product To evaluate this we start with the term Next, we evaluate the j term. THERE IS AN INHERENT NEGATIVE SIGN TO THIS TERM. The determinant of the remaining 2 x 2 matrix is calculated in a similar fashion

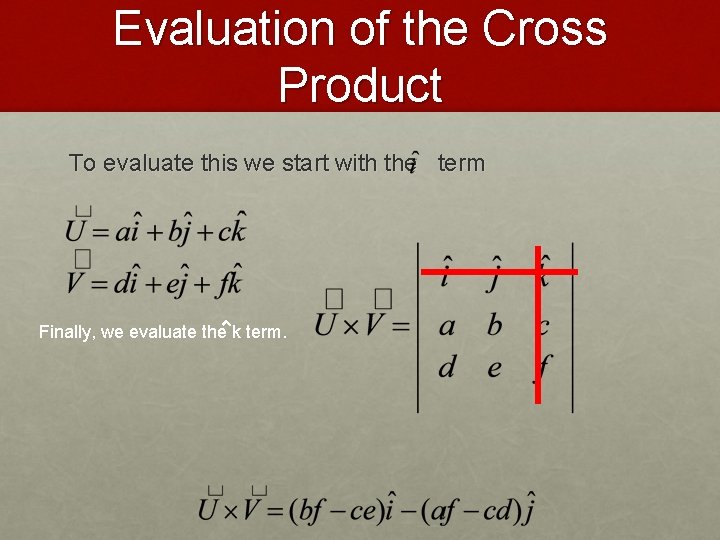
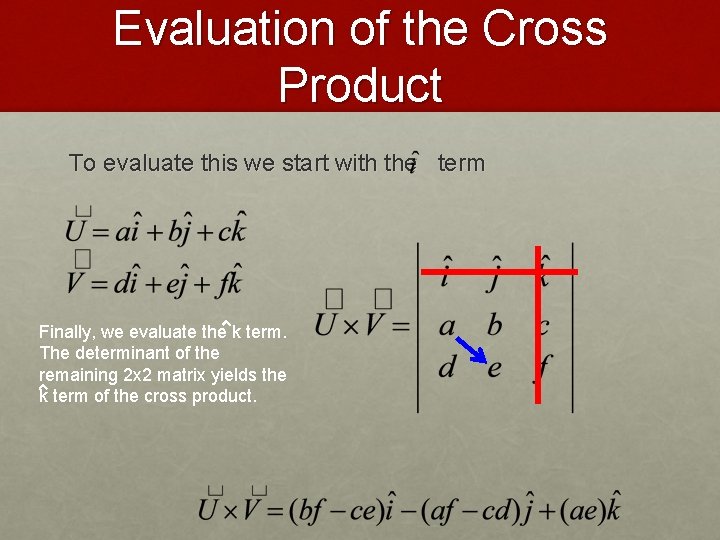
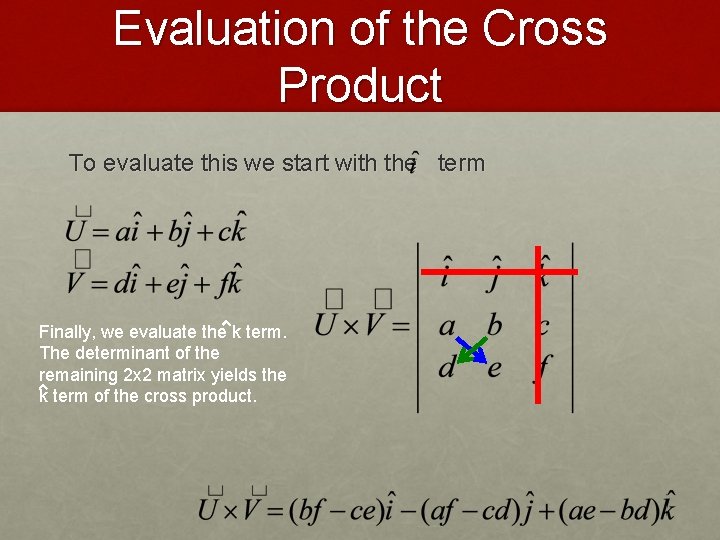
Evaluation of the Cross Product To evaluate this we start with the term Finally, we evaluate the k term.

Evaluation of the Cross Product To evaluate this we start with the term Finally, we evaluate the k term. The determinant of the remaining 2 x 2 matrix yields the k term of the cross product.

Evaluation of the Cross Product To evaluate this we start with the term Finally, we evaluate the k term. The determinant of the remaining 2 x 2 matrix yields the k term of the cross product.

Evaluation of the Cross Product To evaluate this we start with the term The units of this vector will be the product of the units of the vectors used to calculate the cross product.

Properties of the Cross Product Anti-commutative:

Properties of the Cross Product Anti-commutative: Not associative:

Properties of the Cross Product Anti-commutative: Not associative: Distributive:

Properties of the Cross Product Anti-commutative: Not associative: Distributive: Scalar Multiplication:

Other Facts about the Cross Product The cross product of 2 parallel vectors is 0

Other Facts about the Cross Product The cross product of 2 parallel vectors is 0 The magnitude of the cross product is equal to the area of a parallelogram bounded by 2 vectors

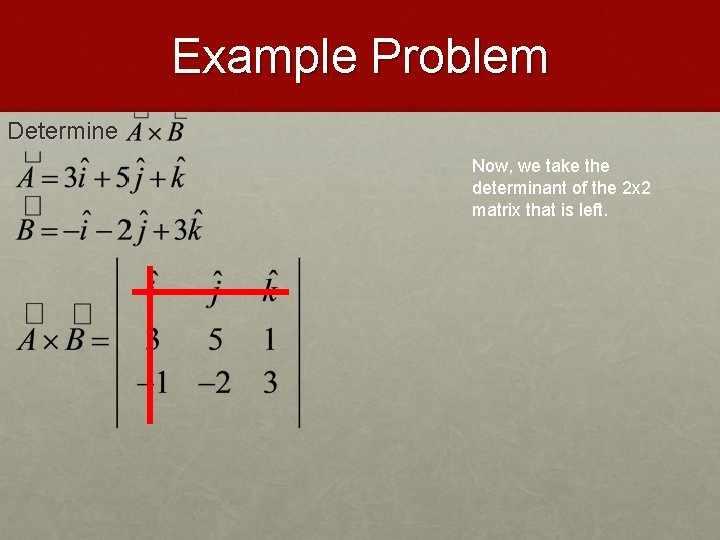
Example Problem Determine

Example Problem Determine First, we set up the matrix for the cross product evaluation

Example Problem Determine To evaluate the i term, we need to disregard the row and column i is found in.

Example Problem Determine Now, we take the determinant of the 2 x 2 matrix that is left.

Example Problem Determine Multiply the diagonal that goes from the upper left of the matrix to its lower right.

Example Problem Determine Subtract the product from the other diagonal to complete the i term.

Example Problem Determine Remember that there is an inherent minus sign in the j term.

Example Problem Determine The j term is found by disregarding the row and column it’s found in, and taking the determinant of the remaining 2 x 2 matrix

Example Problem Determine The j term is found by disregarding the row and column it’s found in, and taking the determinant of the remaining 2 x 2 matrix

Example Problem Determine The k term is found by disregarding the row and column it’s found in, and taking the determinant of the remaining 2 x 2 matrix

Example Problem Determine The j term is found by disregarding the row and column it’s found in, and taking the determinant of the remaining 2 x 2 matrix

Example Problem Determine The j term is found by disregarding the row and column it’s found in, and taking the determinant of the remaining 2 x 2 matrix

Example Problem Determine Now we can simplify the equation

Example Problem Determine Now we can simplify the equation

Example Problem Determine Now we can simplify the equation