VECTOR OPERATIONS 5 Coplanar Forces Vectors Resultant If

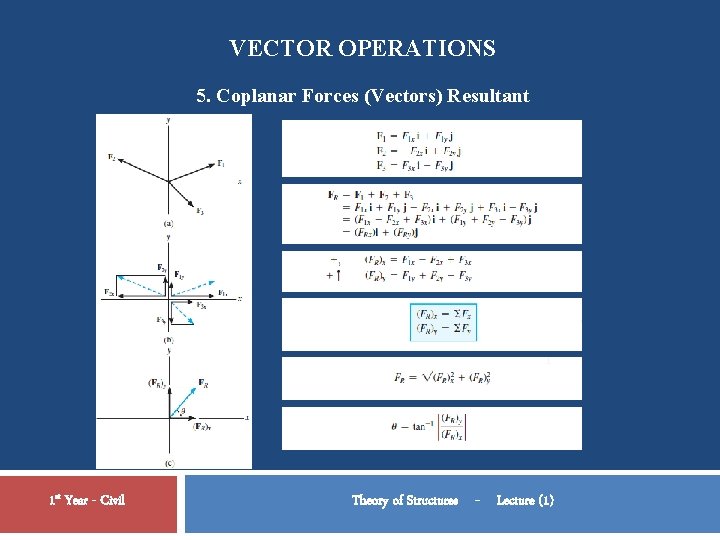
VECTOR OPERATIONS 5. Coplanar Forces (Vectors) Resultant If more than two forces are to be added, successive applications of the parallelogram law can be carried out in order to obtain the resultant force. For example, if three forces F 1, F 2, F 3 act at a point O, Fig. 2– 9, the resultant of any two of the forces is found, say, F 1 + F 2—and then this resultant is added to the third force, yielding the resultant of all three forces; i. e. , FR = (F 1 + F 2) + F 3. 1 st Year - Civil Theory of Structures - Lecture (1)

VECTOR OPERATIONS 5. Coplanar Forces (Vectors) Resultant 1 st Year - Civil Theory of Structures - Lecture (1)

MOMENT OF A FORCE When a force is applied to a body it will produce a tendency for the body to rotate about a point that is not on the line of action of the force. This tendency to rotate is sometimes called a torque, but most often it is called the moment of a force or simply the moment. 1 st Year - Civil Theory of Structures - Lecture (1)

RESULTANT MOMENT For two-dimensional problems, where all the forces lie within the x–y plane, the resultant moment (MR)O about point O (the z axis) can be determined by finding the algebraic sum of the moments caused by all the forces in the system. As a convention, we will generally consider positive moments as counterclockwise since they are directed along the positive z axis (out of the page). Clockwise moments will be negative. Doing this, the directional sense of each moment can be represented by a plus or minus sign. Using this sign convention, with a symbolic curl to define the positive direction, the resultant moment is therefore: 1 st Year - Civil Theory of Structures - Lecture (1)

MOMENT OF A COUPLE A couple is defined as two parallel forces that have the same magnitude, but opposite directions, and are separated by a perpendicular distance d. 1 st Year - Civil Theory of Structures - Lecture (1)

HISTORICAL BACKGROUND q The fact that some of the magnificent structures from earlier eras, such as Egyptian pyramids (about 3000 b. c. ), Greek temples (500– 200 b. c. ), Roman coliseums and aqueducts (200 b. c. –a. d. 200), and Gothic cathedrals (a. d. 1000– 1500), still stand today is a testimonial to the ingenuity of their builders. q Galileo Galilei (1564– 1642) is generally considered to be the originator of theory of structures. In his book entitled Two New Sciences, which was published in 1638, Galileo analyzed the failure of some simple structures, including cantilever beams. 1 st Year - Civil Theory of Structures - Lecture (1)