Vector modes vorticity and magnetic fields Kobayashi RM

Vector modes, vorticity and magnetic fields Kobayashi, RM, Shiromizu, Takahashi: PRD, astro-ph/0701596 Caprini, Crittenden, Hollenstein, RM: PRD, ar. Xiv: 0712. 1667 Lu, Ananda, Clarkson, RM: JCAP, ar. Xiv: 0812. 1349 Roy Maartens Institute of Cosmology and Gravitation University of Portsmouth April 2009

Generating B and ω at O(1) • Maxwell in Minkowski spacetime • 4 -current • Faraday tensor

Maxwell’s equations 2 • General spacetime – The fundamental object is the Faraday tensor – Electric and magnetic fields depend on the observer – Charge and current densities depend on the observer

Maxwell’s equations 3 • Expanding FRW universe background: at O(1):

Then Maxwell’s equations in an expanding FRW universe become, at O(1) where is the comoving derivative is the conformal time derivative are the comoving (lab) fields

• In the cosmic plasma, up to O(1): Then are both transverse (‘pure’ vector) • The metric at O(1), with only vector perturbations, is (in Poisson gauge) • To generate B from zero at O(1), we need a current – and the current must be transverse, i. e. with nonzero curl • We need a nonzero difference between vorticities

Take the curl of the curl B equation and use the curl E equation to get the wave equation: Thus, at O(1) This is the basis of Harrison’s mechanism (1970) • Electrons are tightly coupled to photons, but not so tightly to protons. • Radiation fluid (γ+e) spins down at a different rate to the proton fluid.

At O(1), the vorticity is given in terms of velocity and metric perturbations by This follows from the covariant definition of vorticity:

At O(1), according to Harrison, we need In particular, the proton and photon velocities must be different – whereas the electron velocity can be the same as the photon velocity and we can in principle still get a current that sources B The velocities evolve according to the momentum balance equations:

The force density terms are a sum of scattering terms and electromagnetic force densities: Lorentz force = O(2) The are Thomson and Coulomb rates. Then we get the momentum balance equations:

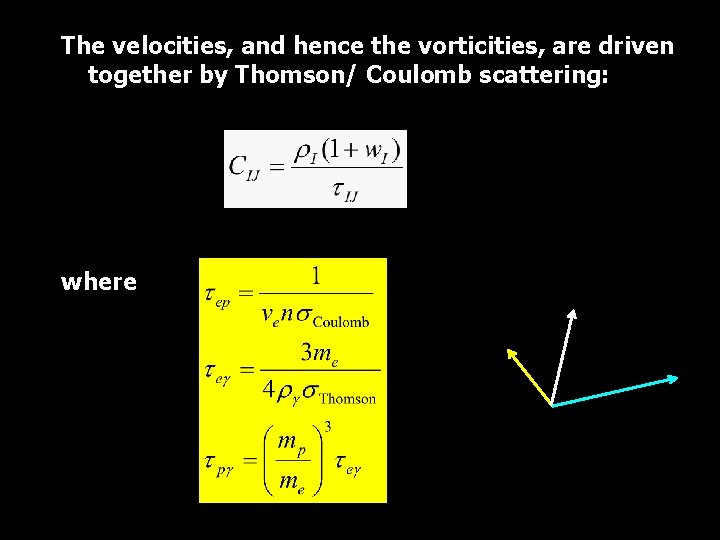
The velocities, and hence the vorticities, are driven together by Thomson/ Coulomb scattering: where

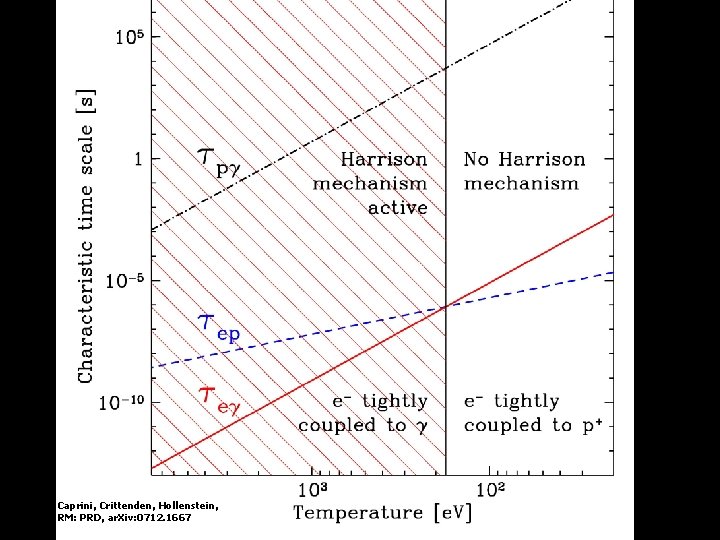
Caprini, Crittenden, Hollenstein, RM: PRD, ar. Xiv: 0712. 1667

How to get vorticity? • Harrison’s mechanism: * electrons bound to photons (Thomson) * protons can have different velocity * if there is primordial vorticity – then a rotational current arises at O(1) * this generates a B-field • The key issue = how to get primordial vorticity at O(1)? • NOT from inflation • Defects (eg strings) actively generate vector perturbations at O(1) • This should source vorticity in the plasma?

• BUT - the total plasma vorticity is conserved: momentum balance is – and B is sourced by the initial total vorticity:

• Thus there is a closed loop, independent of the defects • The defects cannot induce plasma vorticity at O(1) • Defects induce metric vector perturbations – but the plasma velocities respond to conserve total plasma vorticity:

Ways out of the closed loop • O(1) anisotropic stress in the plasma But anisotropic stress is suppressed at high T - by collisions • At O(2): defects can directly generate plasma motions via turbulence, as they move through the plasma (Battefeld et al, ar. Xiv: 0708. 2901)

Alternative: O(2) vectors from density perturbations • Density perturbations generate at O(2) a cosmological background of vector modes and O(1)

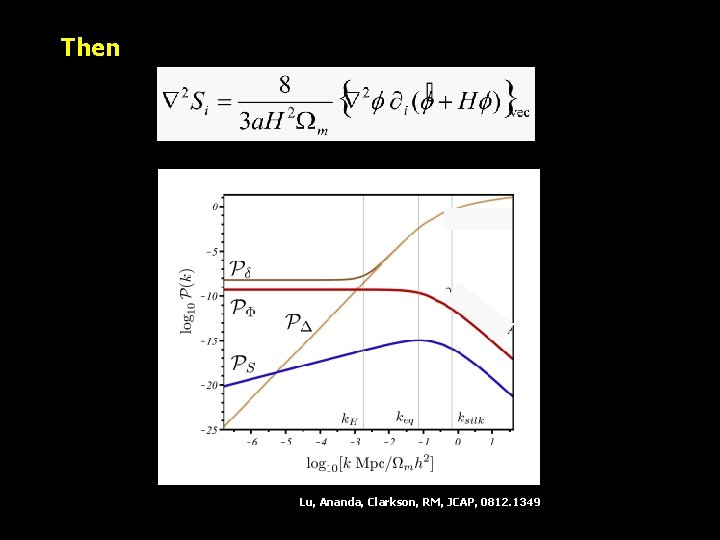
Then a a Lu, Ananda, Clarkson, RM, JCAP, 0812. 1349

• In principle, the O(2) vector background affects – ISW – Lensing – redshift-space distortions • But – no vorticity is generated in the dust matter at O(2): (This is basically the Kelvin-Helmholtz theorem. ) • In fact, at all nonlinear orders, no vorticity can be generated in a perfect fluid:

• For a general fluid, kinematic quantities defined via • Energy-momentum tensor (in the energy frame): • Momentum conservation (nonlinear): • Vorticity propagation (nonlinear): only source is curl acceleration

Use the nonlinear identity NB: curl grad ≠ 0 and the vanishing of anisotropic stress, to get where For a perfect (adiabatic) fluid, pnad=0, and vorticity is conserved to all orders.

To generate vorticity, we need: • Nonadiabaticity (with ) O(2) – also generates B (Biermann battery) • Anisotropic stress O(1) – but need vector stress • Momentum exchange with another fluid O(2) – also generates B (Kobayashi, RM, Shiromizu, Takahashi, PRD, astro-ph/0701596)