Vector Models for IR Gerald Salton Cornell Salton

Vector Models for IR Boolean Model Doc V 1 0 0 0 1 0

Example DNA Compiler Comput* C++ Sparc genome bilog* protein Doc V 1 3 5

Queries and Documents share same vector representation D 1 D 2 Q D 3

Similarity Functions • Many other options available(Dice, Jaccard) • Cosine similarity is self normalizing

Projection of Vectors into 2 -D Plane V 5 V 1 V 2 V

C 1 C 2 Centroid computation : Basically, the average of the vectors in

Hierarchical Search with Document Centroids V 1 V 2 V 3 V 4 V

Hierarchical Query Matching VQ = Query Vector Ci = Root Centroid For all children

Sample Clustered Document Collection document vector r centroid vector CS 466 -8 11

Ideal Document Space ¡ relevant document with respect to a queryvector r nonrelevant document

Introduction of Superclusters document vector r centroid vector supercentroid vector CS 466 -8 13

Slides: 13

Download presentation

Vector Models for IR • Gerald Salton, Cornell (Salton + Lesk, 68) (Salton, 71) (Salton + Mc. Gill, 83) • SMART System Chris Buckely, Cornell / SAPIR systems g Current keeper of the flame Salton’s Magical Automatic Retrieval Tool(? ) CS 466 -8 1

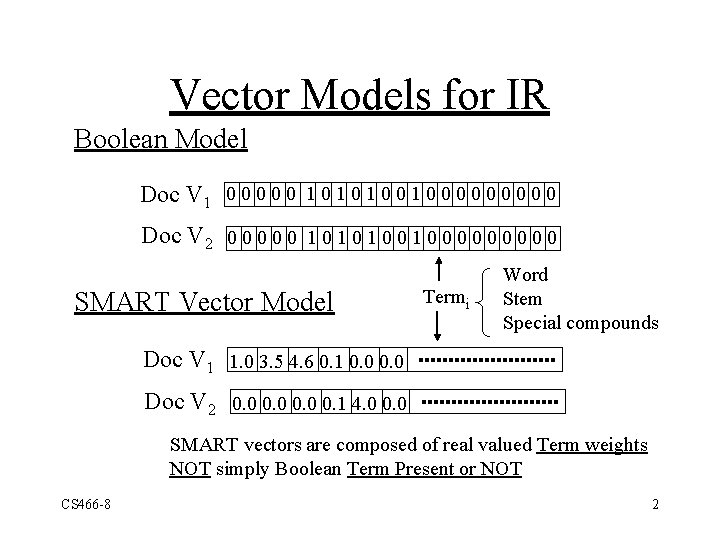
Vector Models for IR Boolean Model Doc V 1 0 0 0 1 0 1 0 0 0 0 0 Doc V 2 0 0 0 1 0 1 0 0 0 0 0 SMART Vector Model Termi Word Stem Special compounds Doc V 1 1. 0 3. 5 4. 6 0. 1 0. 0 Doc V 2 0. 0 0. 1 4. 0 0. 0 SMART vectors are composed of real valued Term weights NOT simply Boolean Term Present or NOT CS 466 -8 2

Example DNA Compiler Comput* C++ Sparc genome bilog* protein Doc V 1 3 5 4 1 0 0 Doc V 2 1 0 0 0 5 3 1 4 Doc V 3 2 8 0 1 0 0 Issues • How are weights determined? (simple option : jraw freq. kweighted by region, titles, keywords) • Which terms to include? Stoplists • Stem or not? CS 466 -8 3

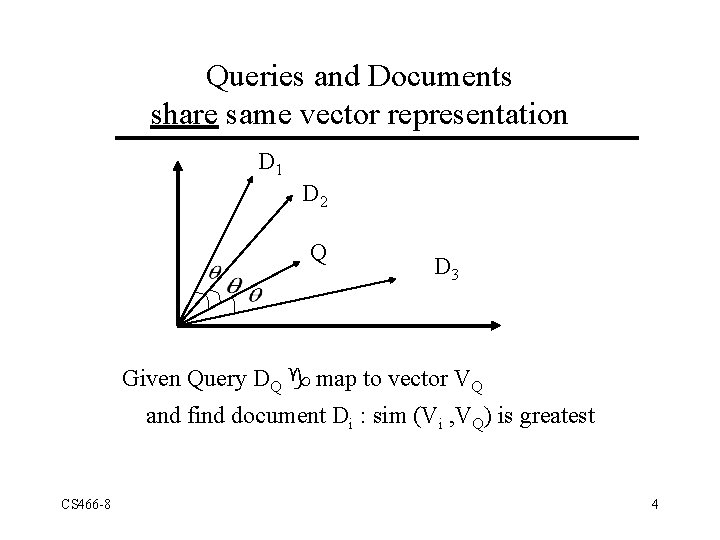
Queries and Documents share same vector representation D 1 D 2 Q D 3 Given Query DQ g map to vector VQ and find document Di : sim (Vi , VQ) is greatest CS 466 -8 4

Similarity Functions • Many other options available(Dice, Jaccard) • Cosine similarity is self normalizing V 1 100 200 300 50 V 2 1 2 3 0. 5 V 3 10 20 30 5 D 2 Q D 3 Can use arbitrary integer values (don’t need to be probabilities) CS 466 -8 5

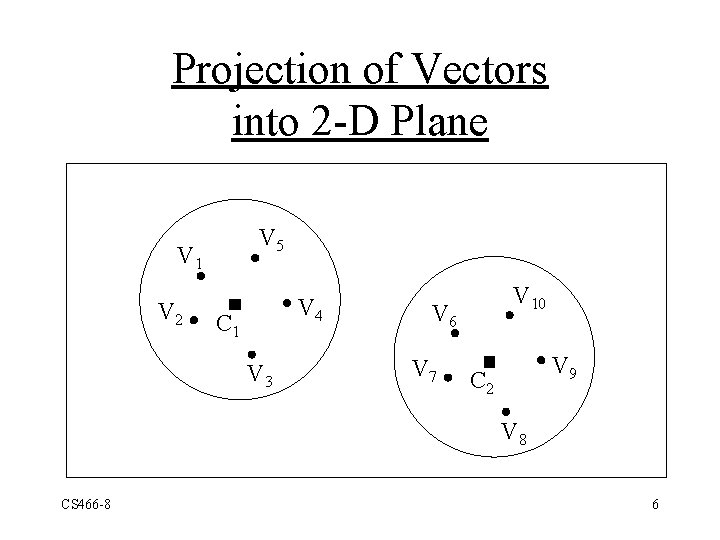
Projection of Vectors into 2 -D Plane V 5 V 1 V 2 V 4 C 1 V 3 V 10 V 6 V 7 V 9 C 2 V 8 CS 466 -8 6

C 1 C 2 Centroid computation : Basically, the average of the vectors in the centroid set D = documents in centroid set Total docs in centroid set CS 466 -8 7

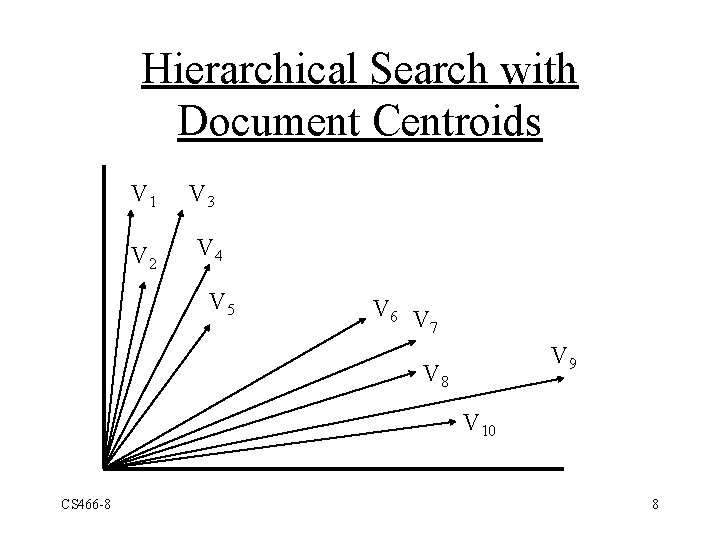
Hierarchical Search with Document Centroids V 1 V 2 V 3 V 4 V 5 V 6 V 7 V 9 V 8 V 10 CS 466 -8 8

Hierarchical Query Matching VQ = Query Vector Ci = Root Centroid For all children of Ci {Cj } • find Cj : sim (VQ , Cj) is maximum • if Cj is a leaf(document vector), return Cj • else Ci = Cj and iterate log ( | D | ) vector comparisons (height of tree) CS 466 -8 9

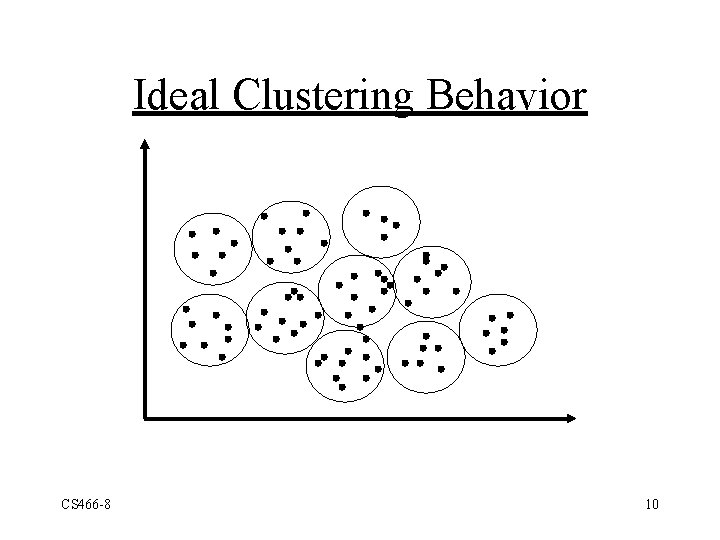
Ideal Clustering Behavior CS 466 -8 10

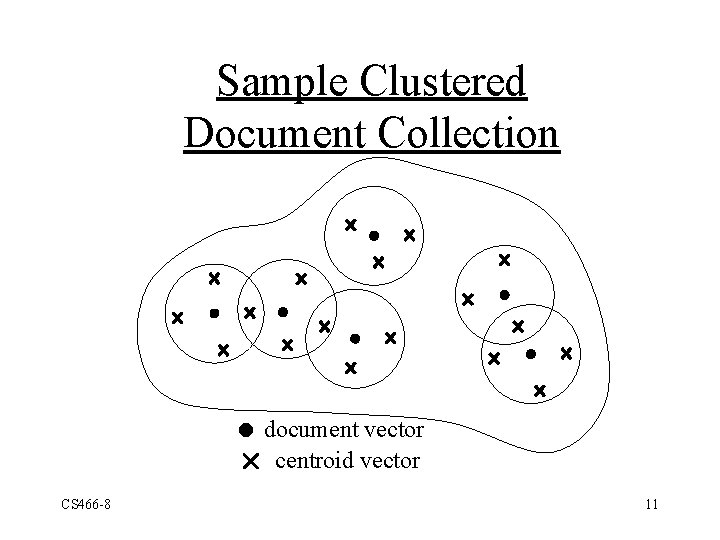
Sample Clustered Document Collection document vector r centroid vector CS 466 -8 11

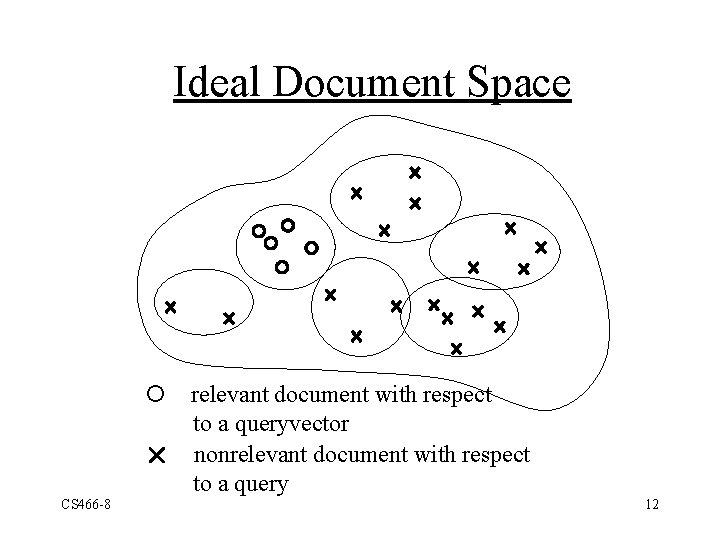
Ideal Document Space ¡ relevant document with respect to a queryvector r nonrelevant document with respect to a query CS 466 -8 12

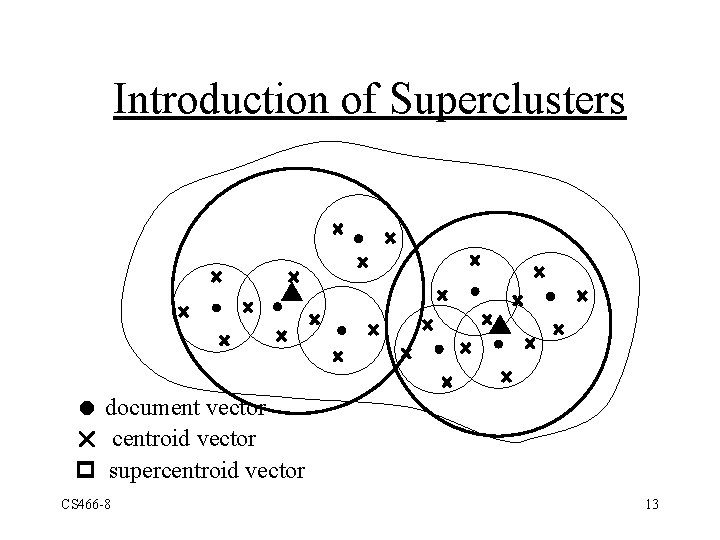
Introduction of Superclusters document vector r centroid vector supercentroid vector CS 466 -8 13