Vector Model v Vector space model or term

Vector Model

v Vector space model (or term vector model): an algebraic model used for information retrieval, and relevancy rankings. It represents natural language documents in a formal manner by the use of vectors in a multi-dimensional space based on an origin. 2

Vector Space Model v Most commonly used strategy is the vector space model (proposed by Salton in 1975) v It recognize that the use of binary weights is too limiting and propose a framework in which partial matching is possible. v Partial matching is accomplished by assigning non-binary weights to index term in queries and documents. 3

The idea v Vector space model in steps : 1) associate a weight to Each Term in document and query. 2) Documents and Queries are mapped into term vector space. 3) Similarity method is used to compute the degree of similarity between each document stored in the system and user query. 4) Documents are ranked by closeness to the query. 4

Weights for Term Components v Parameters in calculating a weight for a document term or query term: § Term Frequency (tf): Term Frequency is the number of times a term i appears in document j (tfij) § Document Frequency (df): Number of documents a term i appears in, (dfi). § Inverse Document Frequency (idf): A discriminating measure for a term i in collection, i. e. , how discriminating term i is. (the term which appear in many documents are not very useful for distinguishing a relevant document from irrelevant one) (idfi) = log 10 (N/ ni), where N= number of documents in the collection ni = number of document that contain the term i Remark : consider ni/N as a probability of selecting document that contain a query term in it. 5

Computing weights wi, j (tf-idf) v How can we compute the values of the weights wi, j ? § One of the most popular methods is based on combining two factors: • The importance of each index term in the document (tf) • The importance of the index term in the collection of documents (idf) § Combining these two factors we can obtain the weight of an index term i as : wij = tfij * idfi = tfij * log 10 (N/ ni) Where: N= number of documents in the collection ni = number of document that contain the term i § Also called the tf-idf weighting scheme 6

Similarity Measure v A similarity measure is a function that computes the degree of similarity between two vectors( Document and Query) v Using a similarity measure between the query and each document: § It is possible to rank the retrieved documents in the order of relevance. § It is possible to enforce a certain threshold so that the size of the retrieved set can be controlled. 7

Similarity Methods v Inner Product (dot Product) v Cosine v Jaccard v Dice 8

9

definitions Ø For weighted term vectors Ø Xi is the weight of term i in document k and Yi is the weight of term i in the query. Ø For binary term vectors: Ø |X| is the number of terms occur in X (document ). Ø |Y| is the number of terms occur in Y (query ). Ø |X ∩ Y| is the number of terms occur in both X and Y. 10

Similarity function output v Result from these functions are interval[0 - 1] • By Values near 1. 0 means document and query are more relevant. • By Values near 0. 0 mean documents and query are less relevant. 11

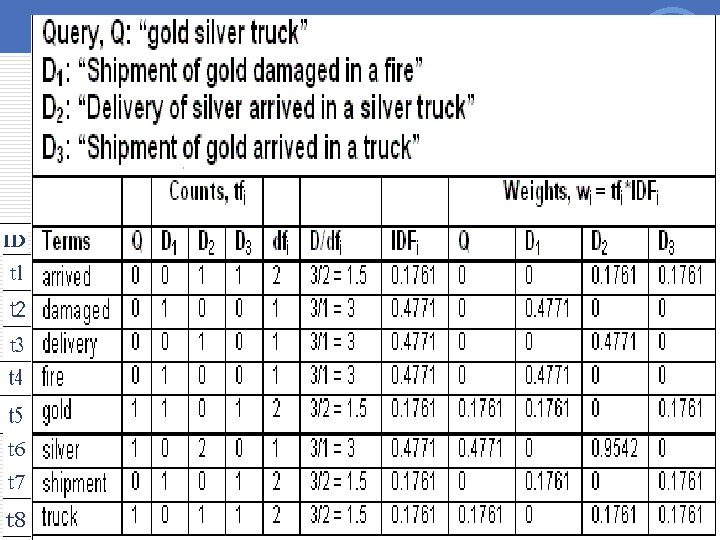
Vector Model Example v by Professors David Grossman and Ophir Frieder, from the Illinois Institute of Technology(the authors of the book “Information Retrieval: Algorithms and Heuristics”. ) available through Amazon. COM Stop Words D 1: “Shipment of gold delivered in a fire” D 2: “Delivery of silver arrived in a silver truck” D 3: “Shipment of gold arrived in a truck” Q: “gold silver truck” 12

Vector Model Example v let assume we deal with a basic term vector model in which we : 1. do not take into account WHERE the terms occur in documents. (documents consist of passages and passages consist of sentences ) 2. Remove stopwords. 3. do not reduce terms to root terms (stemming). 4. use raw frequencies for terms and queries (unnormalized data). 13

Vector Model Example 14

Vector Model Example Cont… Now we need to find similarity measures by using Similarity Methods. q Inner Product (Dot Product) Ø SC (Q, D 1)=(0)(0) + (0)(0. 477) + (0. 176) + (0)(0)=0. 0309 Ø SC (Q, D 2)=0. 4862 Ø SC (Q, D 3)=0. 0620 15

Vector Model Example Cont… Document ID Similarity score D 1 0. 0309 D 2 0. 4862 D 3 0. 0620 5. Now, we rank the documents in a descending order according to their similarity score, as the following: Document ID Similarity score D 2 0. 4862 (most relevant) D 3 0. 0620 D 1 0. 0309 We can use threshold to retrieve documents above the value of that threshold. 16

Vector Model Example Cont… q Cosine Where , Inner product the inner product and length for documents and query. 17 is the

Vector Model Example Cont… v For cosine method we must calculate the length of each documents and the length of query as the following: § Length of 0. 7195 § Length of 1. 095 § Length of 0. 352 § Length of 0. 538 D 1 = sqrt(0. 477^2+0. 176^2+0. 176^2)= D 2 = sqrt(0. 176^2+0. 477^2+0. 954^2+0. 176^2)= D 3 = sqrt(0. 176^2+0. 176^2)= Q = sqrt(0. 1761^2+0. 477^2+0. 1761^2)= v Inner product for each document is: § D 1= 0. 0309 § D 2=0. 4862 § D 3=0. 0620 18

Vector Model Example Cont… v Then the similarity values are: § cos. Sim(D 1, Q) = 0. 0309 / 0. 719 * 0. 538 = 0. 0801 § cos. Sim(D 2, Q) = 0. 4862 / 1. 095 * 0. 538 = 0. 8246 § cos. Sim(D 3, Q) = 0. 061 / 0. 352 * 0. 538 = 0. 3271 v Now, we rank the documents in a descending order according to their similarity score, as the following Document ID Similarity score D 2 0. 8246 (most relevant) D 3 0. 3271 0. 0801 D 1 19

Vector Model Example Cont… q Jaccard Where is the inner product and is the square of summation of the weight of each term in each document and which is the summation of the weight of each term in the query 20

Vector Model Example Cont… v Inner product for each document is: § D 1= 0. 0309 § D 2=0. 4862 § D 3=0. 0620 v The square of the summation of the weight of each term in each document is: § = (0. 477^2+0. 176^2+0. 176^2)= 0. 515 § = (0. 176^2+0. 477^2+0. 954^2+0. 176^2)= 1. 989 § = (0. 176^2+0. 176^2)= 0. 124 v square of the summation of the weight of each term in the query is : = (0. 176^2+0. 477^2+0. 176^2)= 0. 289 21

Vector Model Example Cont… v Then the similarity values are: § Jac. Sim(D 1, Q) = 0. 0309 / (0. 517 + 0. 289 - 0. 0309) = 0. 0399 § Jac. Sim(D 2, Q) = 0. 4862 / (1. 989 + 0. 289 - 0. 4862) = 0. 271 § Jac. Sim(D 3, Q) = 0. 0620 / (0. 124 + 0. 289 - 0. 0620) = 0. 177 § Now, we rank the documents in a descending order according to their similarity score, as the following Document ID Similarity score D 2 0. 323 (most relevant) D 3 0. 177 D 1 0. 0399 22

Binary Term Vector Example v Binary: § X = 1, 1, 1, 0, § Y = 1, 0 , 1, 0, v Jaccard Similarity 1, 0, 1, 1, v Jac. Sim(X, Y)=3/(5+4 -3)=0. 5 23 0 1

Dissimilarity Between Objects v Some popular ones include: Minkowski distance: where (xi 1, xi 2, …, xip) and (xj 1, xj 2, …, xjp) are two p-dimensional data objects, and q is a positive integer v If q = 1, d is Manhattan distance 24

Dissimilarity Between Objects (Cont. ) v If q = 2, d is Euclidean distance: § Properties • d(i, j) 0 • d(i, i) = 0 • d(i, j) = d(j, i) • d(i, j) d(i, k) + d(k, j) 25

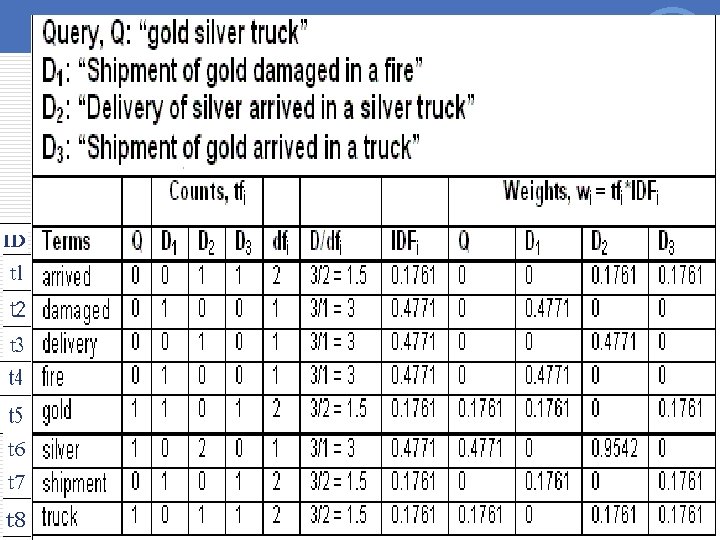
Vector Model Example 26

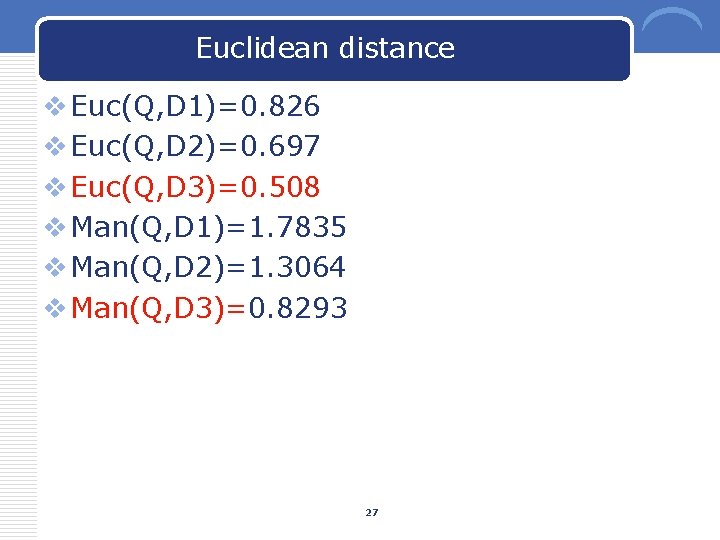
Euclidean distance v Euc(Q, D 1)=0. 826 v Euc(Q, D 2)=0. 697 v Euc(Q, D 3)=0. 508 v Man(Q, D 1)=1. 7835 v Man(Q, D 2)=1. 3064 v Man(Q, D 3)=0. 8293 27