Vector Field Visualization T Moeller H Shen slide

Vector Field Visualization * T. Moeller, H. Shen 의 slide를 이용함.

Vector Field Visualization -A vector field: F(U) = V U: field domain (x, y) in 2 D (x, y, z) in 3 D V: vector (u, v) or (u, v, w) - Like scalar fields, vectors are defined at discrete points

Flow Visualization • Flow visualization – classification – Dimension (2 D or 3 D) – Time-dependency: steady vs. unsteady – Grid type • In most cases numerical methods required for flow visualization

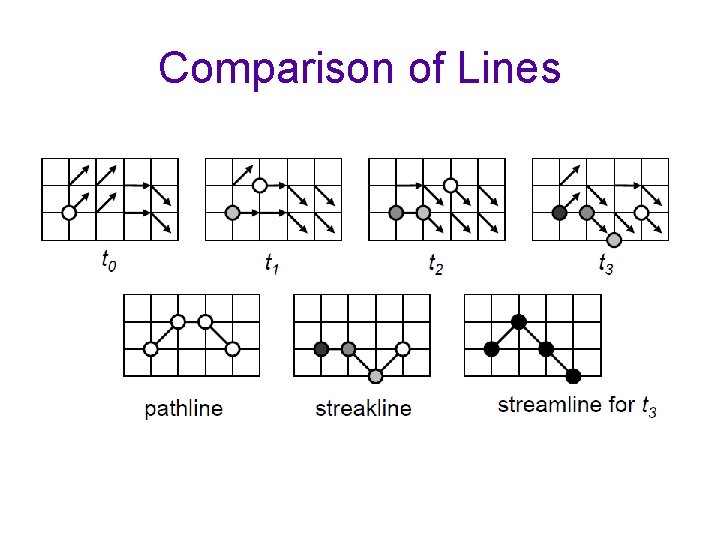
Characteristic of Lines • Streamline – tangential to the vector field • Pathline – trajectories of massless particles in the flow • Streakline – trace of dye that is released into the flow at a fixed position • Time line (Time surface) – propagation of a line (surface) of massless elements in time

Streamlines • Tangential to the vector field • Vector field at an arbitrary, yet fixed time t • Streamline is a solution to the initial value problem of an ordinary differential equation • Streamline is curve L(u) with the parameter u

Pathlines • Trajectories of massless particles in the flow • Vector field can be time-dependent (unsteady) • Pathline is a solution to the initial value problem of an ordinary differential equation:

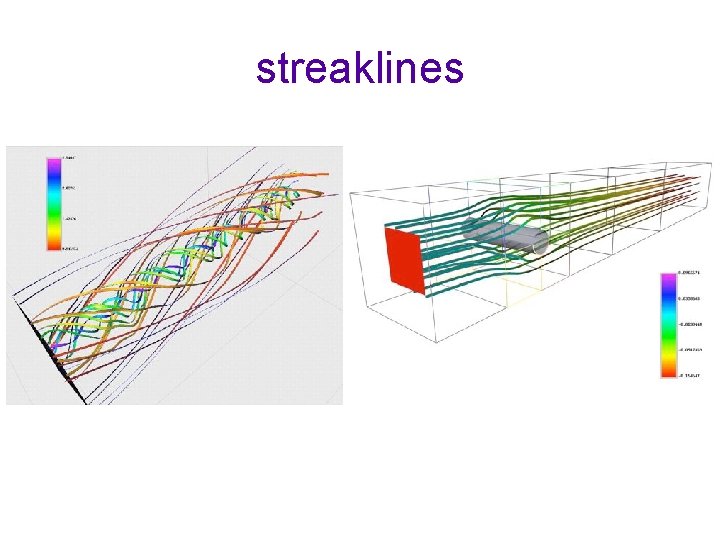
Streaklines • Trace of dye that is released into the flow at a fixed position • Connect all particles that passed through a certain position

Time lines (Time surfaces) t 0 • Propagation of a line (surface) of massless elements in time • Idea: “consists” of many point-like particles that are traced • Connect particles that were released simultaneously t 1 t 2 Timelines or time surfaces can show the evolution of a flow.

Example : streamline, pathline, streakline The red particle moves in a flowing fluid; Its pathline is traced in red; the tip of the trail of blue ink released from the origin follows the particle, but unlike the static pathline (which records the earlier motion of the dot), ink released after the red dot departs continues to move up with the flow. (This is a streakline. ) The dashed lines represent contours of the velocity field (streamlines), showing the motion of the whole field at the same time.

Comparison of Lines

Pathline

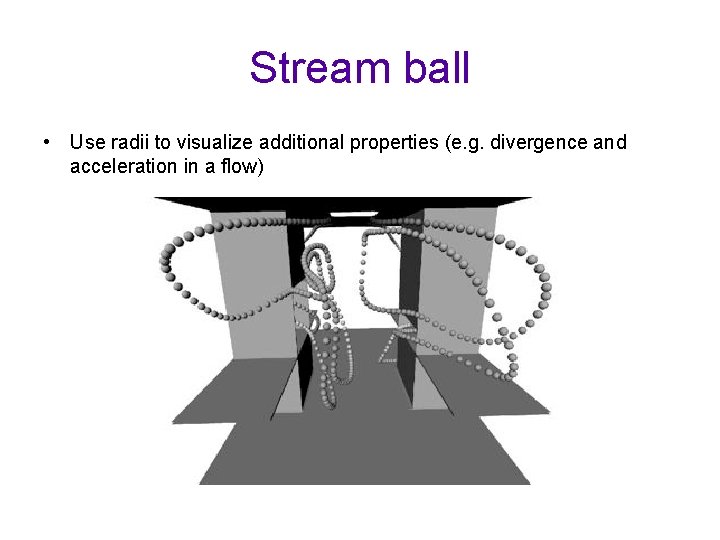
Stream ball • Use radii to visualize additional properties (e. g. divergence and acceleration in a flow)

streaklines

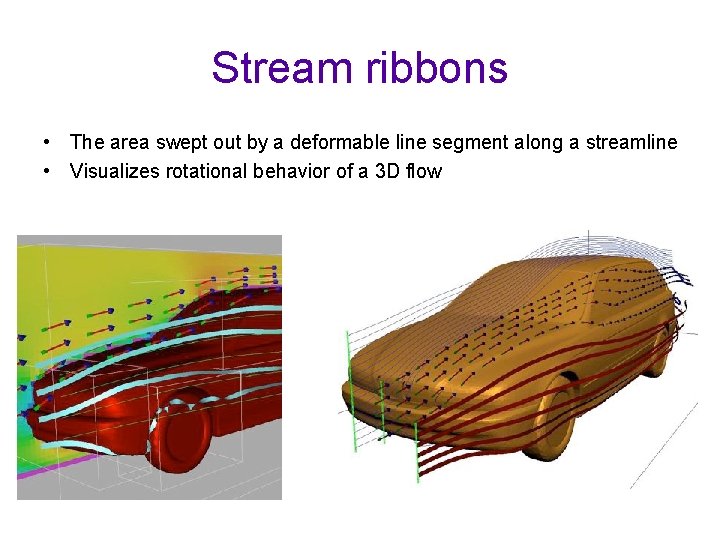
Stream ribbons • The area swept out by a deformable line segment along a streamline • Visualizes rotational behavior of a 3 D flow

streamtubes • Thick tube shaped streamline whose radial extent shows the expansion of flow

Local technique - Particle Tracing Visualizing the flow directions by releasing particles and calculating a series of particle positions based on the vector field The motion of particle: dx/dt = v(x) x: particle position (x, y, z) v(x): the vector (velocity) field Use numerical integration to compute a new particle position x(t+dt) = x(t) + Integration( v(x(t)) dt )

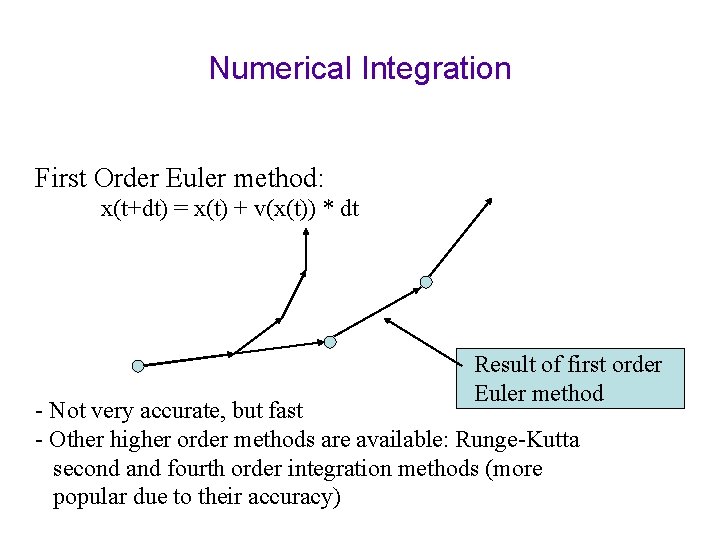
Numerical Integration First Order Euler method: x(t+dt) = x(t) + v(x(t)) * dt Result of first order Euler method - Not very accurate, but fast - Other higher order methods are available: Runge-Kutta second and fourth order integration methods (more popular due to their accuracy)

Numerical Integration (2) Second Runge-Kutta Method x(t+dt) = x(t) + ½ * (K 1 + K 2) k 1 = dt * v(x(t)) k 2 = dt * v(x(t)+k 1) x(t+dt) x(t) ½ * [v(x(t))+v(x(t)+dt*v(x(t))]

Numerical Integration (3) Standard Method: Runge-Kutta fourth order x(t+dt) = x(t) + 1/6 (k 1 + 2 k 2 + 2 k 3 + k 4) k 1 = dt * v(t); k 2 = dt * v(x(t) + k 1/2) k 3 = dt * v(x(t) + k 2/2); k 4 = dt * v(x(t) + k 3)

Arrows and Glyphs • Visualize local features of the vector field: – Vector itself – Vorticity – Extern data: temperature, pressure, etc. • Important elements of a vector: – Direction – Magnitude – Not: components of a vector • Approaches: – Arrow plots – Glyphs

Arrows • Arrows visualize – Direction of vector filed – Magnitude • Length of arrows • Color coding

Glyphs • Can visualize more features of the vector field

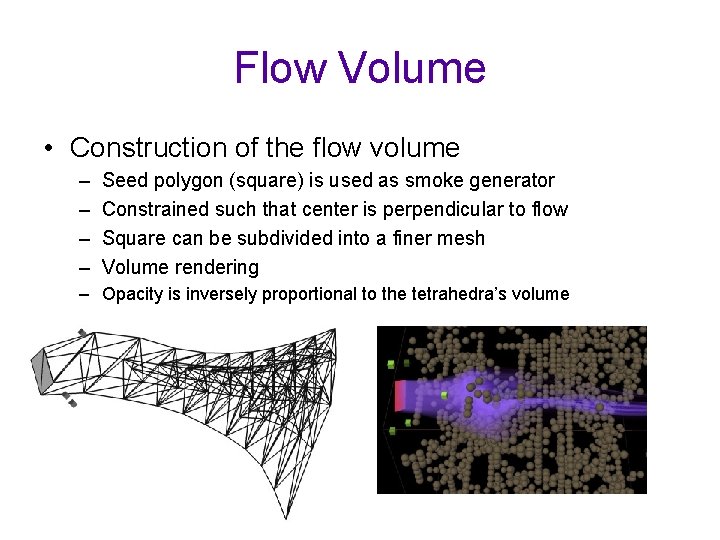
Flow Volume • Construction of the flow volume – – Seed polygon (square) is used as smoke generator Constrained such that center is perpendicular to flow Square can be subdivided into a finer mesh Volume rendering – Opacity is inversely proportional to the tetrahedra’s volume

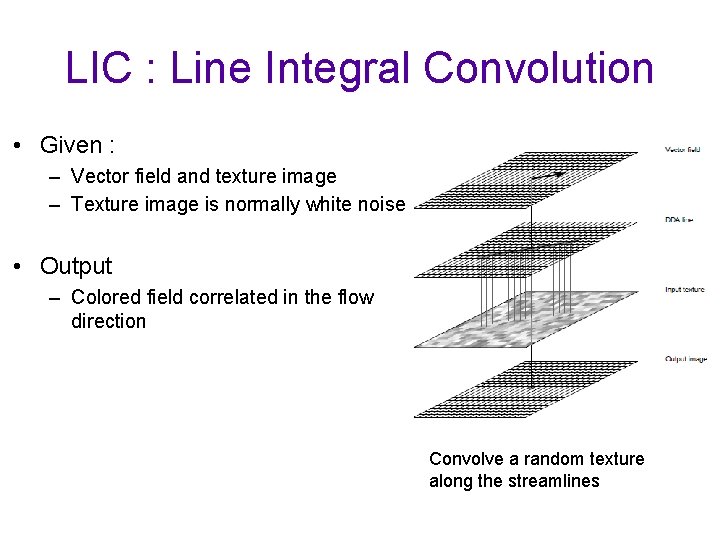
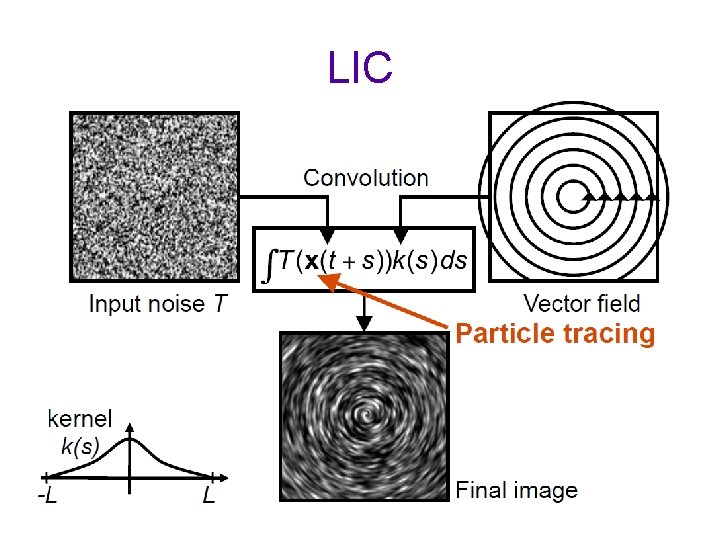
LIC : Line Integral Convolution • Given : – Vector field and texture image – Texture image is normally white noise • Output – Colored field correlated in the flow direction Convolve a random texture along the streamlines

LIC • Visualize dense flow fields by imaging its integral curves • Cover domain with a random texture (so called ‚input texture‘, usually stationary white noise) • Blur (convolve) the input texture along the path lines using a specified filter kernel

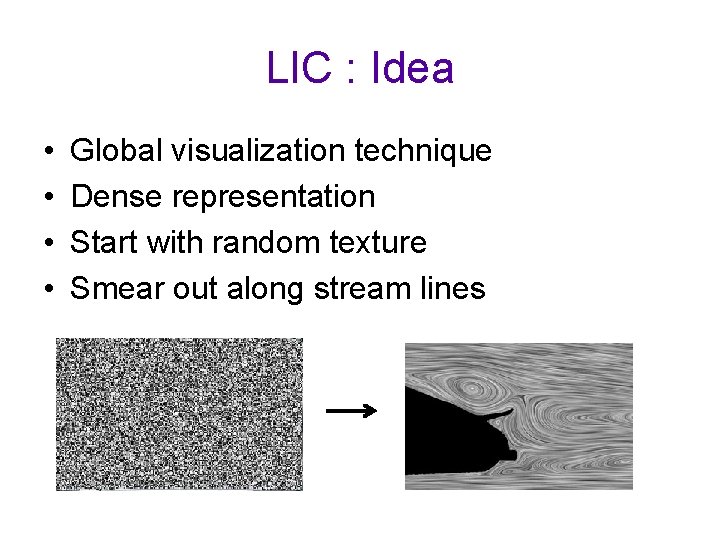
LIC : Idea • • Global visualization technique Dense representation Start with random texture Smear out along stream lines

example

LIC Algorithm

LIC

OLIC : Oriented Line Integral Convolution • Visualizes orientation (in addition to direction) • Use – Sparse texture – Anisotropic convolution kernel

OLIC

세부적인 이슈 소개 • Illumination • Seed Placement

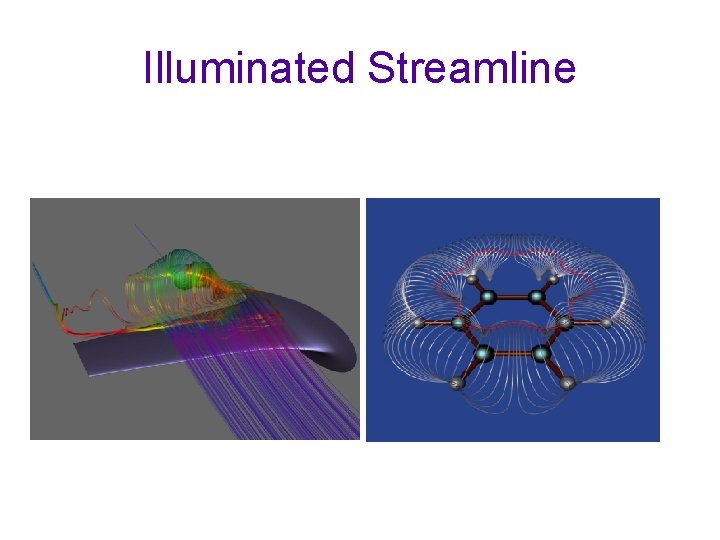
Illuminated Streamline

Comparisons Fully opaque Use transparency With Illumination

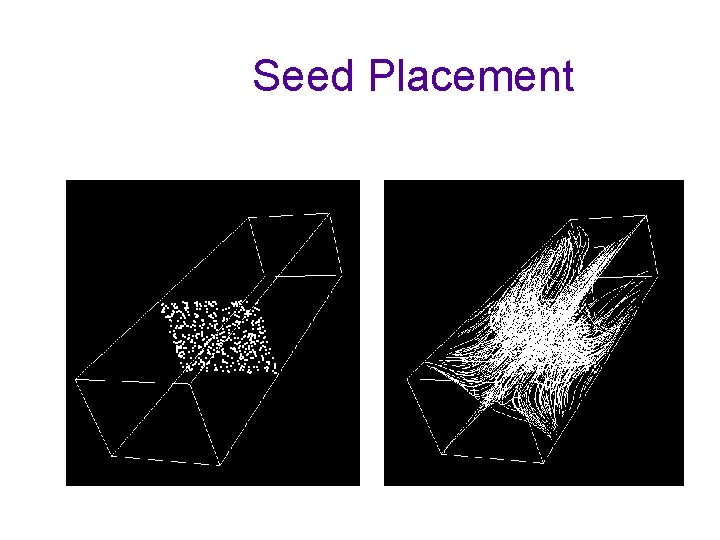
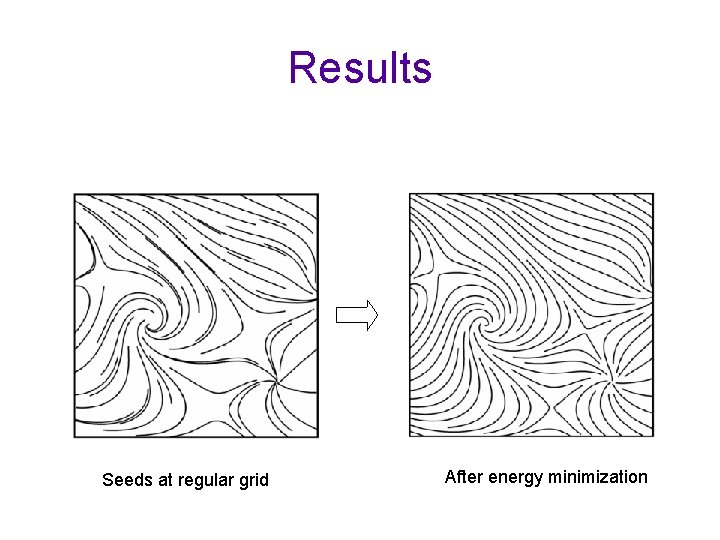
Seed Placement for Streamline • The placement of seeds directly determines the visualization quality – Too many: scene cluttering – Too little: no pattern formed • It has to be the right number at the right places!!!

Seed Placement

Image-Guided Streamline Placement • Main idea: the distribution of ink on the screen should be even [turk 96]

Use Energy Function as a Metric • A energy function is defined to measure whether ‘ink’ is distributed evenly S S ( L*I (x, y) - t ) 2 x y • I(x, y): image with streamlines • L: A low pass filter (Gaussian or Hermit interpolation) • t: A user specified threshold for average image intensity

Iterative Algorithm • Place an initial set of seeds and compute streamlines • Iteratively minimize the energy function (random decent) with the following operations on the seeds: – – – Move Insert Delete Lengthen Shorten Combine • Iterate until the energy function converges

Results Seeds at regular grid After energy minimization