Vector Field Visualization A vector field FU V

Vector Field Visualization -A vector field: F(U) = V U: field domain (x, y) in 2 D (x, y, z) in 3 D V: vector (u, v) or (u, v, w) - Like scalar fields, vectors are defined at discrete points

Vector Field Viz Applications Computational Fluid Dynamics Weather modeling

Vector Field Visualization Challenges General Goal: Display the field’s directional information Domain Specific: Detect certain features Vortex cores, Swirl

Vector Field Visualization Challenges A good vector field visualization is difficult to get: - Displaying a vector requires more visual attributes (u, v, w): direction and magnitude - Displaying a vector requires more screen space more than one pixel is required to display an arrow ==> It becomes more challenging to display a dense vector field

Vector Field Visualization Techniques Local technique: Particle Advection Display the trajectory of a particle starting from a particular location Global technique: Hedgehogs, Line Integral Convolution, Texture Splats etc Display the flow direction everywhere in the field

Local technique - Particle Tracing Visualizing the flow directions by releasing particles and calculating a series of particle positions based on the vector field The motion of particle: dx/dt = v(x) x: particle position (x, y, z) v(x): the vector (velocity) field Use numerical integration to compute a new particle position x(t+dt) = x(t) + Integration( v(x(t)) dt )

Numerical Integration First Order Euler method: x(t+dt) = x(t) + v(x(t)) * dt Result of first order Euler method - Not very accurate, but fast - Other higher order methods are avilable: Runge-Kutta second and fourth order integration methods (more popular due to their accuracy)

Numerical Integration (2) Second Runge-Kutta Method x(t+dt) = x(t) + ½ * (K 1 + K 2) k 1 = dt * v(x(t)) k 2 = dt * v(x(t)+k 1) x(t+dt) x(t) ½ * [v(x(t))+v(x(t)+dt*v(x(t))]

Numerical Integration (3) Standard Method: Runge-Kutta fourth order x(t+dt) = x(t) + 1/6 (k 1 + 2 k 2 + 2 k 3 + k 4) k 1 = dt * v(t); k 2 = dt * v(x(t) + k 1/2) k 3 = dt * v(x(t) + k 2/2); k 4 = dt * v(x(t) + k 3)

Streamlines A curves that connect all the particle positions

Streamlines (cont’d) - Displaying streamlines is a local technique because you can only visualize the flow directions initiated from one or a few particles - When the number of streamlines is increased, the scene becomes cluttered - You need to know where to drop the particle seeds - Streamline computation is expensive

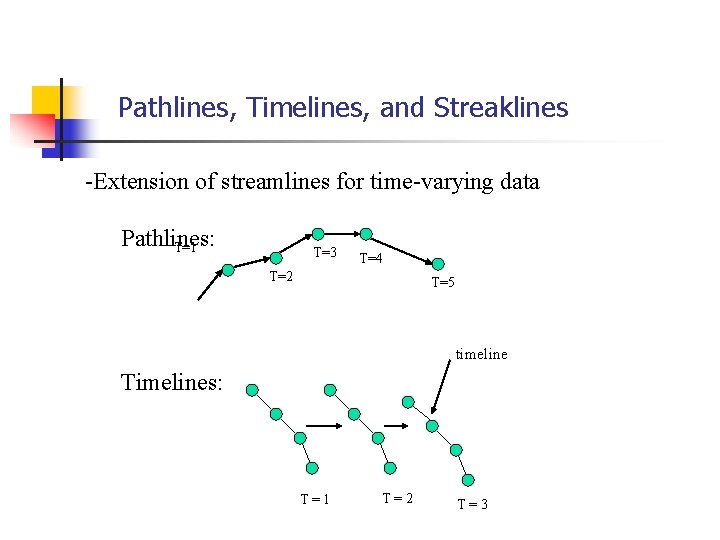
Pathlines, Timelines, and Streaklines -Extension of streamlines for time-varying data Pathlines: T=1 T=3 T=4 T=2 T=5 timeline Timelines: T=1 T=2 T=3

Streaklines - Continuously injecting a new particle at each time step, advecting all the existing particles and connect them together into a streakline b. t. =2 b. t. =3 b. t. =4 b. t. =5 b. t. =1

Global techniques - Display the entire flow field in a single picture - Minimum user intervention - Example: Hedgehogs (global arrow plots)

Hedgehogs - Dense 2 D fields or 3 D fields are difficult

Line Integral Convolution (LIC)

LIC Example

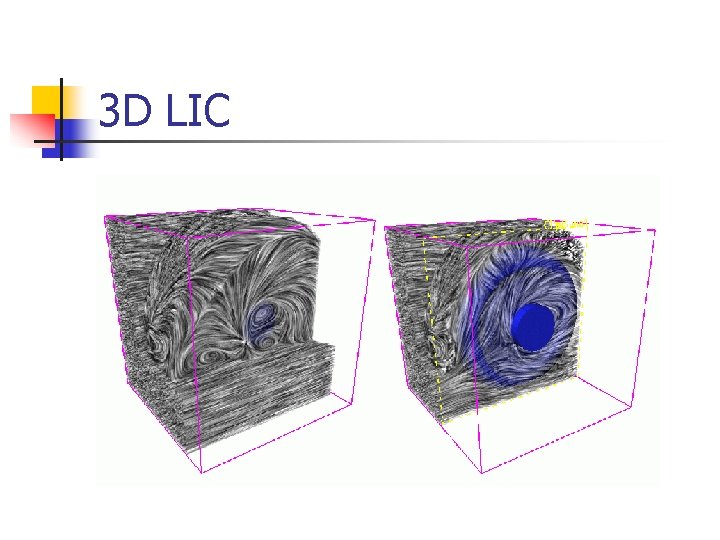
3 D LIC

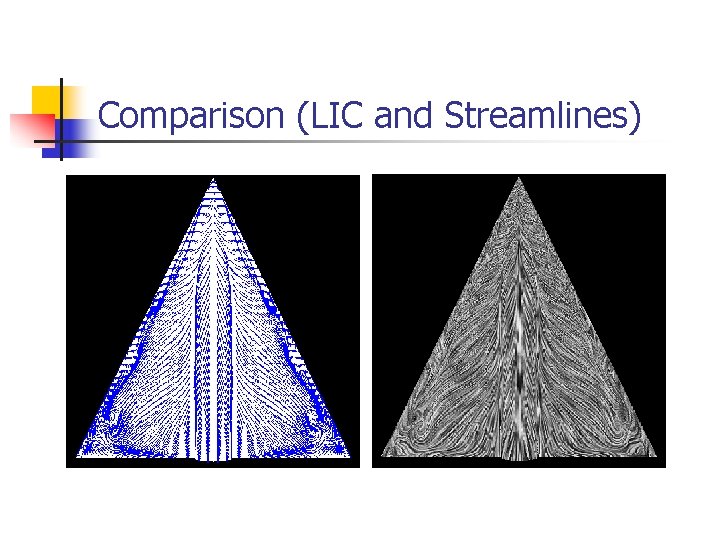
Comparison (LIC and Streamlines)

LIC on 3 D surfaces and volumes

More global techniques Texture Splats

Spot Noise

Line bundles