Vector Electromagnetic Scattering from Layered Rough Surfaces with

Vector Electromagnetic Scattering from Layered Rough Surfaces with Buried Discrete Random Media for Subsurface and Root-Zone Soil Moisture Sensing Xueyang Duan and Mahta Moghaddam Radiation Laboratory, Dept. of EECS, University of Michigan IGARSS, Vancouver, Canada, July 24 – 29, 2011 3/10/2021 1

Outline • • • Motivation and Background Problem Description Formulation Model Validation Simulation results Conclusion and Future Work 3/10/2021 2

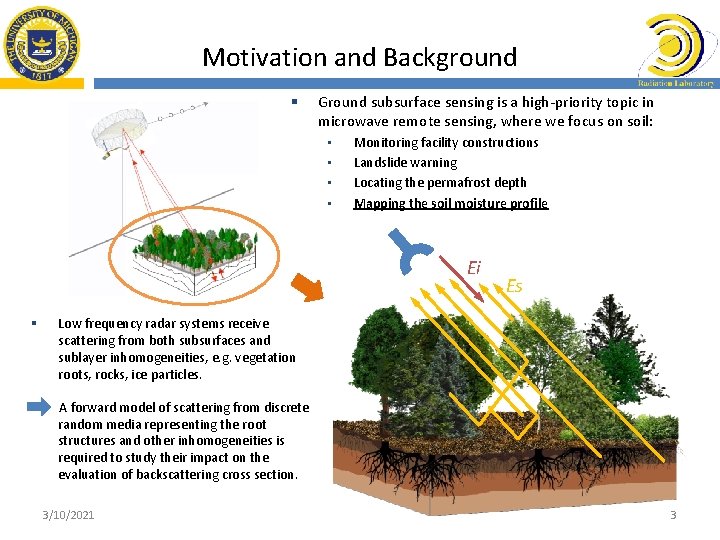
Motivation and Background § Ground subsurface sensing is a high-priority topic in microwave remote sensing, where we focus on soil: • • Monitoring facility constructions Landslide warning Locating the permafrost depth Mapping the soil moisture profile Ei § Es Low frequency radar systems receive scattering from both subsurfaces and sublayer inhomogeneities, e. g. vegetation roots, rocks, ice particles. A forward model of scattering from discrete random media representing the root structures and other inhomogeneities is required to study their impact on the evaluation of backscattering cross section. 3/10/2021 3

Significant Contribution • In the past investigations: – 3 D single or multilayer rough surface scattering model without considering sublayer inhomogeneities – No 3 D full wave solution to random media scattering, especially with rough surfaces • In this work: – First time to include the sublayer inhomogeneities, especially vegetation roots, in the subsurface scattering model – 3 D full wave solution to scattering from discrete random media, especially root-like clusters, with rough surface 3/10/2021 4

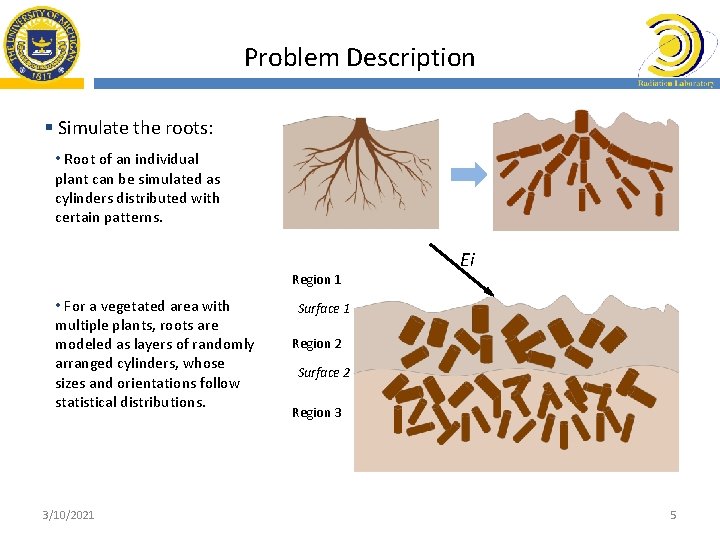
Problem Description § Simulate the roots: • Root of an individual plant can be simulated as cylinders distributed with certain patterns. Region 1 • For a vegetated area with multiple plants, roots are modeled as layers of randomly arranged cylinders, whose sizes and orientations follow statistical distributions. 3/10/2021 Ei Surface 1 Region 2 Surface 2 Region 3 5

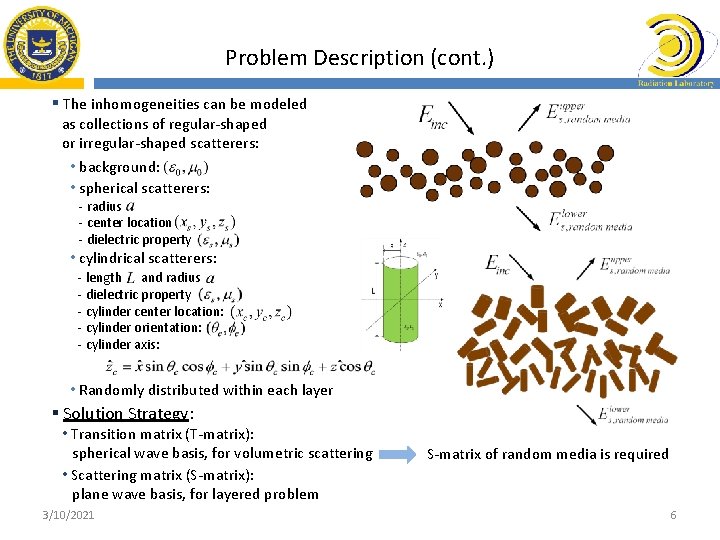
Problem Description (cont. ) § The inhomogeneities can be modeled as collections of regular-shaped or irregular-shaped scatterers: • background: • spherical scatterers: - radius - center location - dielectric property • cylindrical scatterers: - length and radius - dielectric property - cylinder center location: - cylinder orientation: - cylinder axis: • Randomly distributed within each layer § Solution Strategy: • Transition matrix (T-matrix): spherical wave basis, for volumetric scattering • Scattering matrix (S-matrix): plane wave basis, for layered problem 3/10/2021 S-matrix of random media is required 6

Formulation Overview of approach: § Random media of spherical scatterers: • Obtain single sphere T-matrix analytically • Solve multiple sphere scattering using recursive T-matrix method • Obtain S-matrix from T-matrix to S-matrix transformation § Random media of cylindrical scatterers or cylindrical clusters: • Decompose the cylindrical cluster to cascaded short sub-cylinders • Solve single short cylinder T-matrix using extended boundary condition method (EBCM) • Solve T-matrix of random or root-like cylindrical cluster using generalized iterative EBCM and incident field variation • Obtain S-matrix from T-matrix to S-matrix transformation 3/10/2021 7

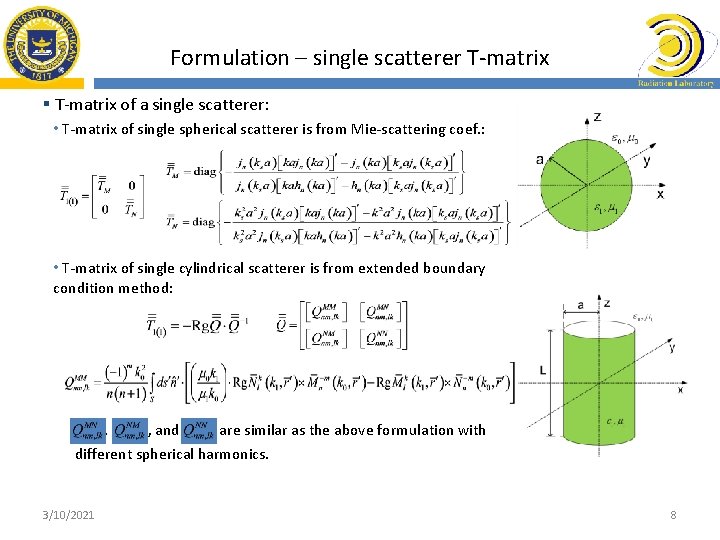
Formulation – single scatterer T-matrix § T-matrix of a single scatterer: • T-matrix of single spherical scatterer is from Mie-scattering coef. : • T-matrix of single cylindrical scatterer is from extended boundary condition method: , , and are similar as the above formulation with different spherical harmonics. 3/10/2021 8

Formulation – aggregate T-matrix (spheres) § Scattering from discrete random media is solved using the recursive T-matrix method § Basic idea: include one scatterer at a time into the cluster, and solve the new T-matrix including interaction between the added scatterer and the rest § Using Addition theorem and translational matrices: Where and are translational matrices § The aggregate T-matrix is computed recursively, 3/10/2021 9

Formulation – Generalized iterative EBCM (cylindrical clusters) § Limitations when considering cylindrical structures representing roots: Ø EBCM: not valid for cylindrical scatterer with large length-to-diameter ratio Ø Recursive T-matrix method: external circumscribed circles of the scatterers must be exclusive Generalized iterative EBCM • • [1]: only valid for vertically oriented long cylinder Our work: generalized to 3 D randomly arranged cylinders • The long cylinder or cylindrical cluster can be treated as cascaded sub-cylinders. • Knowing the T-matrices of all sub-cylinders, scattered field from N sub-cylinders is obtained from iterative procedure: § Iteration starts assuming no field interaction among sub-cylinders § Compute scattered field and update the exciting field on every sub- 2 1 cylinder Repeat till the scattering ofneed all sub-cylinders § Field interactions among coefficients sub-cylinders coordinatesconverge transformation using Addition theorem § Total scattered field is the superposition of scattered fields from all sub-cylinders transformed to the main frame. [1] W. Z. Yan, Y. Du, D. Liu, and B. I. Wu, EM scattering from a long dielectric circular cylinder, PIERS, Vol. 85, pp. 39 -67, 2008. 3/10/2021 10

Formulation – Generalized iterative EBCM (cylindrical clusters) • 3 D coordinates translation is implemented using rotation with z-axis translation. Euler angles are, Rotation (XZX): ith frame to the main frame Description Rotate cylinder axis pointing to the main frame origin Rotate the cylinder frame to be parallel to the main frame Rotation (XZX): main frame to the ith frame Description Rotate z axis pointing to the ith origin Rotate to be the ith frame Where (x’, y’, z’) denotes the coordinates after 1 st rotation, and • T-matrix of the overall cluster: 3/10/2021 11

Formulation – T matrix to S matrix transformation § Scattering matrix is obtained from multipole expansion of plane wave and numerical plane wave expansion of spherical harmonics with near-to-far field transformation. [1] § Transformation: incident plane wave to spherical harmonics, using multipole expansion and Addition theorem Each row ( ) of matrix P corresponds to a given direction of incidence. § Numerical plane wave expansion of vector spherical wave => § non-trivial ! § when , where is an integer relaxation constant, and number of truncated terms in the expansion [Mac. Phie and Wu, 2003], - practically computable in near-field only § Near-to-far field transformation is the § S-matrix can be obtained from the T-matrix as [1] X. Duan and M. Moghaddam, ‘ 3 D Electromagnetic Scattering from Discrete Random Media Comprising Long Finite. Length Cylinders and Root-like Cylinder Clusters’, APS&URSI, Spokane, WA, July 3 – 8, 2011. 3/10/2021 12

Model Validation – Experiment Setup § Vector Network Analyzer and switching matrix based measurement system. • freq: 2. 2 GHz – 2. 8 GHz • 1 transmitter and 14 receivers mounted on an octagon • ‘E’-shape wideband patch antennas • Rotation platform in the center y x § Measurement objects: • PEC/dielectric spheres: dia. 1” • PEC cylinders: length of 2” and 3”, diameter of 3/8, 5/8, 13/16 inches • positioned ‘randomly’ 3/10/2021 13

Model Validation – Simulation § Antenna Model [1]: relating the vector fields and S-parameters measured § Propagation Model: computing the transmission parameter Sji between antennas j and i in the presence of object. With Addition theorem, RX Antenna TX Antenna 3/10/2021 § The cylindrical cluster T-matrix is computed from cascading half-inch sub-cylinder. [1] Haynes, M. , and M. Moghaddam, “Multipole and Sparameter based antenna model, ” IEEE Trans. Antennas Propagat. , vol. 59, no. 1, pp. 225 -235, January 2011 14

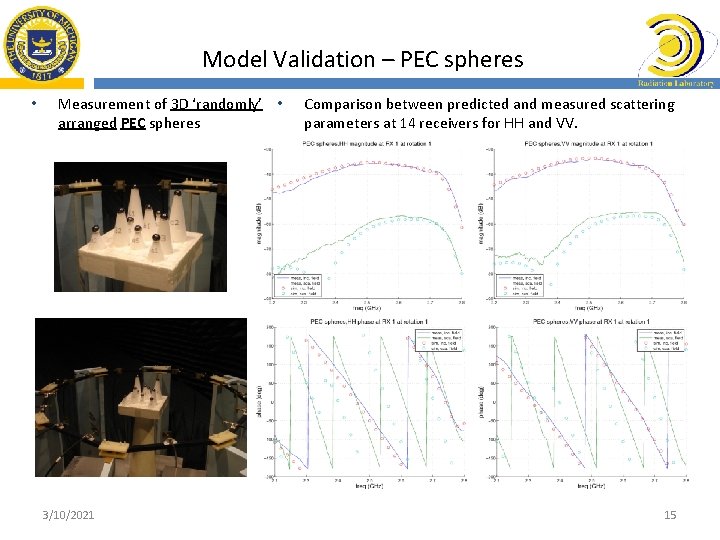
Model Validation – PEC spheres • Measurement of 3 D ‘randomly’ • arranged PEC spheres 3/10/2021 Comparison between predicted and measured scattering parameters at 14 receivers for HH and VV. 15

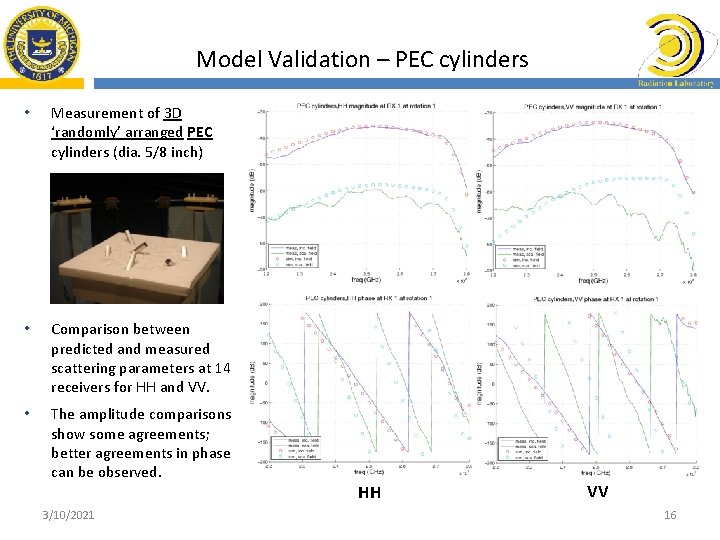
Model Validation – PEC cylinders • Measurement of 3 D ‘randomly’ arranged PEC cylinders (dia. 5/8 inch) • Comparison between predicted and measured scattering parameters at 14 receivers for HH and VV. • The amplitude comparisons show some agreements; better agreements in phase can be observed. 3/10/2021 HH VV 16

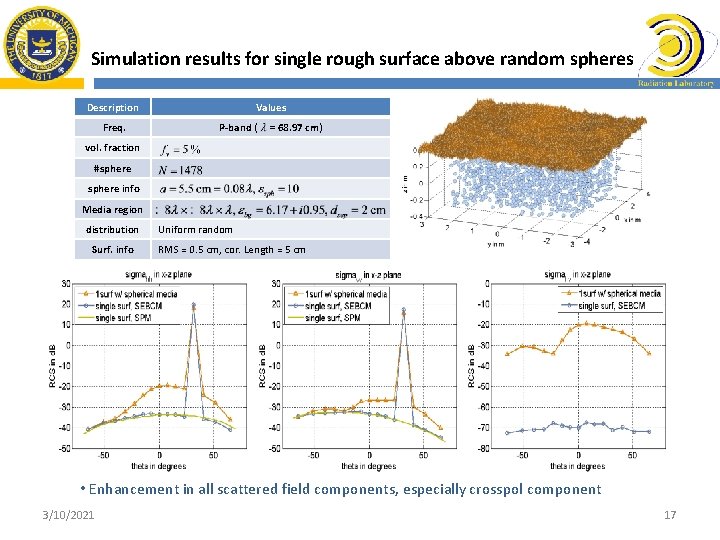
Simulation results for single rough surface above random spheres Description Freq. Values P-band ( = 68. 97 cm) vol. fraction #sphere info Media region distribution Surf. info Uniform random RMS = 0. 5 cm, cor. Length = 5 cm • Enhancement in all scattered field components, especially crosspol component 3/10/2021 17

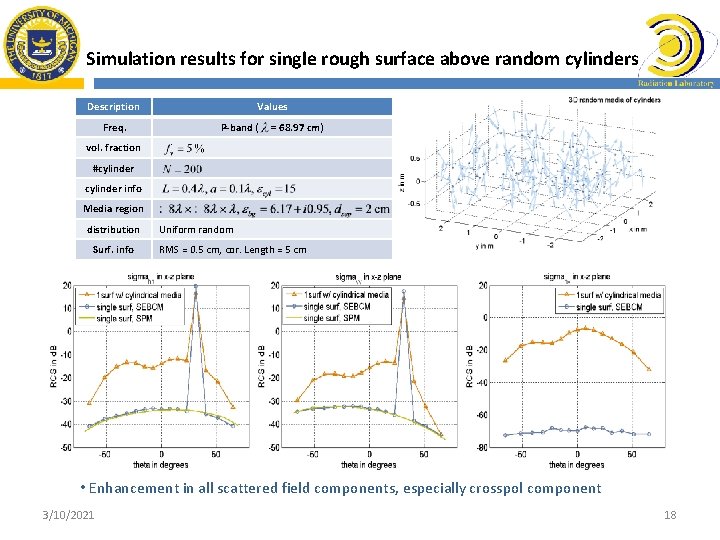
Simulation results for single rough surface above random cylinders Description Freq. Values P-band ( = 68. 97 cm) vol. fraction #cylinder info Media region distribution Surf. info Uniform random RMS = 0. 5 cm, cor. Length = 5 cm • Enhancement in all scattered field components, especially crosspol component 3/10/2021 18

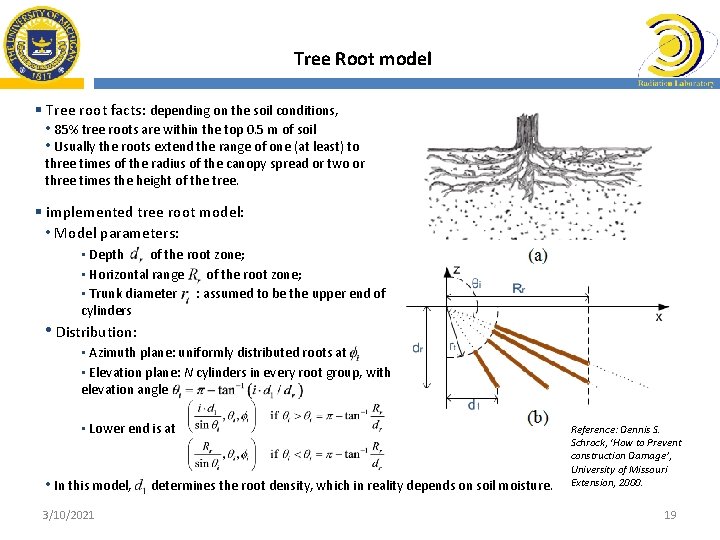
Tree Root model § Tree root facts: depending on the soil conditions, • 85% tree roots are within the top 0. 5 m of soil • Usually the roots extend the range of one (at least) to three times of the radius of the canopy spread or two or three times the height of the tree. § implemented tree root model: • Model parameters: • Depth of the root zone; • Horizontal range of the root zone; • Trunk diameter : assumed to be the upper end of cylinders • Distribution: • Azimuth plane: uniformly distributed roots at • Elevation plane: N cylinders in every root group, with elevation angle • Lower end is at • In this model, 3/10/2021 determines the root density, which in reality depends on soil moisture. Reference: Dennis S. Schrock, ‘How to Prevent construction Damage’, University of Missouri Extension, 2000. 19

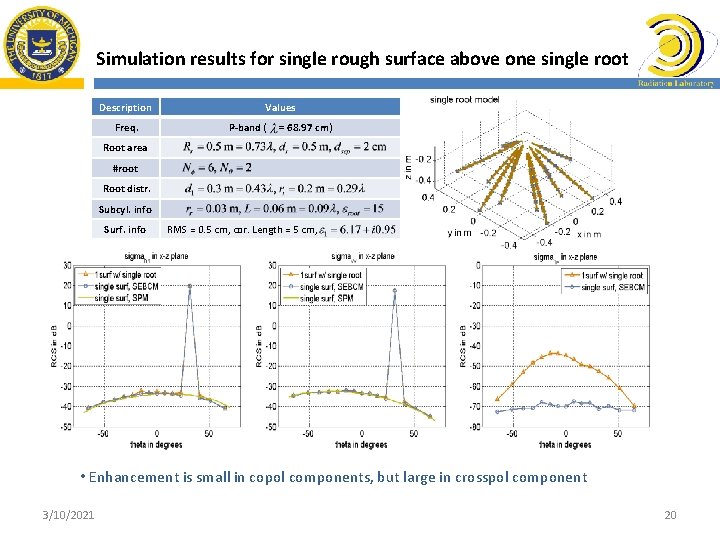
Simulation results for single rough surface above one single root Description Freq. Values P-band ( = 68. 97 cm) Root area #root Root distr. Subcyl. info Surf. info RMS = 0. 5 cm, cor. Length = 5 cm, • Enhancement is small in copol components, but large in crosspol component 3/10/2021 20

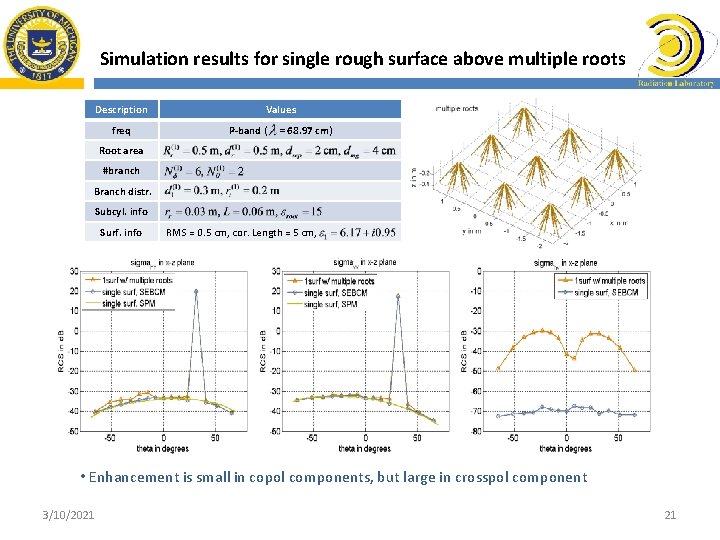
Simulation results for single rough surface above multiple roots Description freq Values P-band ( = 68. 97 cm) Root area #branch Branch distr. Subcyl. info Surf. info RMS = 0. 5 cm, cor. Length = 5 cm, • Enhancement is small in copol components, but large in crosspol component 3/10/2021 21

Conclusion and Future Work In this work, we showed: § Solution to scattering from randomly arranged spherical scatterers § Solution to scattering from randomly arranged cylindrical clusters that can be used to represent root structures § Experimental validation of the scattering model of discrete random media of both spherical and cylindrical scatterers § Simulations results of single rough surface with buried random media or simplified roots § The presence of roots can significantly impact overall scattering cross section from the subsurface, especially in cross-pol § Root geometry, density, and dielectric properties have strong impact on the scattering cross section. Future work: § Further integration of the discrete random media model with multilayer rough surface model, soil moisture profile, and above-ground vegetation § Use in root-zone soil moisture retrieval 3/10/2021 22

Acknowledgement • Measurement setup from Mark Haynes and Steven Clarkson Thank you ! Question? 3/10/2021 23