Vector Components Adding Nonperpendicular Vectors August 24 25

Vector Components & Adding Non-perpendicular Vectors August 24 -25 2015

Vector Components Any vector can be “resolved” into two component vectors. A Ay Ax Ax is the horizontal component – or x component -- of the vector. Ay is the vertical component – or the y component – of the vector.

Example: A plane heads east, while the wind moves a plane north. As a result, the plane moves with velocity of 34 m/s @ 48°relative to the ground. Calculate the plane's heading and wind velocity. What does this mean? ? It means we need to find the x-component of the plane’s resulting velocity (= wind velocity) and the y-component of the plane’s resulting velocity (= plane’s heading). v = 34 m/s @ 48°. Find vx and vy vx vy

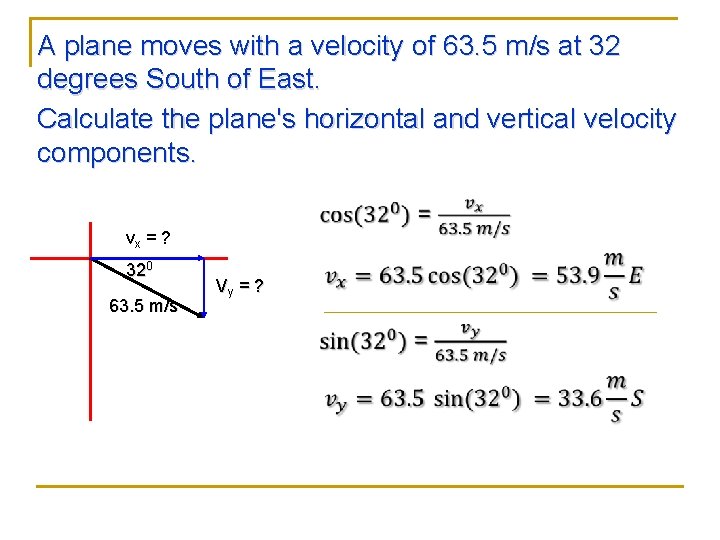
A plane moves with a velocity of 63. 5 m/s at 32 degrees South of East. Calculate the plane's horizontal and vertical velocity components. vx = ? 320 63. 5 m/s Vy = ?

Problems for you to try individually n A person walks 450 m @ 120 degrees. Find the x and y component vectors. n A car accelerates 6 m/s 2 at 40 degrees. Find the x and y component vectors.

Problems for you to try individually A person walks 450 m @ 120 degrees. Find the x and y component vectors. 225 m west = Ax 390 m north = Ay n A car accelerates 6 m/s 2 at 40 degrees. Find the x and y component vectors. 4 m east = Ax 4 m North = Ay n

You can find a vector from its components. This problem may be written differently, but its exactly the same type of problem we did during exactly our first lesson on vectors! Let: Fx = 4 N Just add the components to find the overall Fy = 3 N. vector! Find magnitude and direction of the vector. Fx 2+ Fy 2 = F 2 Fx Fy = arc tan (¾) = 370

So far, we can … • Add two (or more) vectors that occur perpendicularly or in a line (day 1 of vectors) • Find the x and y components of a vector (today) • Determine a vector from its components (today) Can we add two (or more) vectors if they occur at nonright angles? Now, with a little graphical reasoning and vector components … we can!

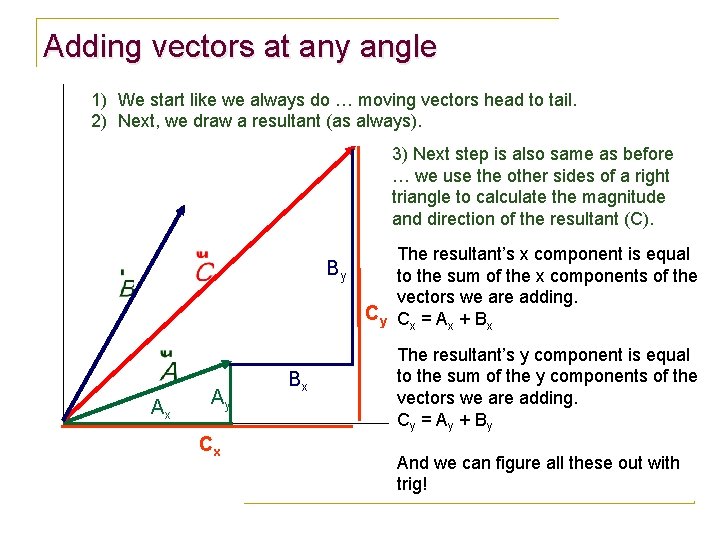
Adding vectors at any angle 1) We start like we always do … moving vectors head to tail. 2) Next, we draw a resultant (as always). 3) Next step is also same as before … we use the other sides of a right triangle to calculate the magnitude and direction of the resultant (C). By Ax Ay Cx Bx The resultant’s x component is equal The difference? We just have to do to the sum of the x components of the a little more reasoning to ‘see’ the vectors we are adding. right triangle and find its sides. Cy Cx = Ax + Bx We can always – ALWAYS – find a The resultant’s y component is equal right triangle that is made from to the sum of the y components of the combining the vector components of vectors we are adding. the vectors we are adding. C = A + B y y y And we can figure all these out with trig!

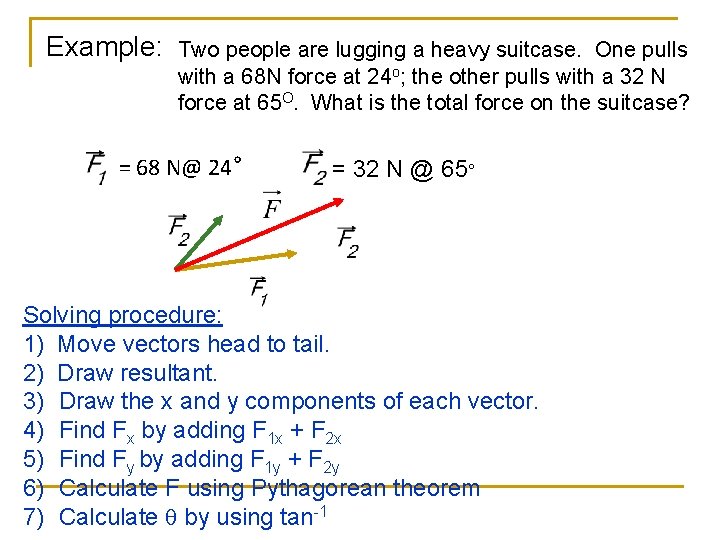
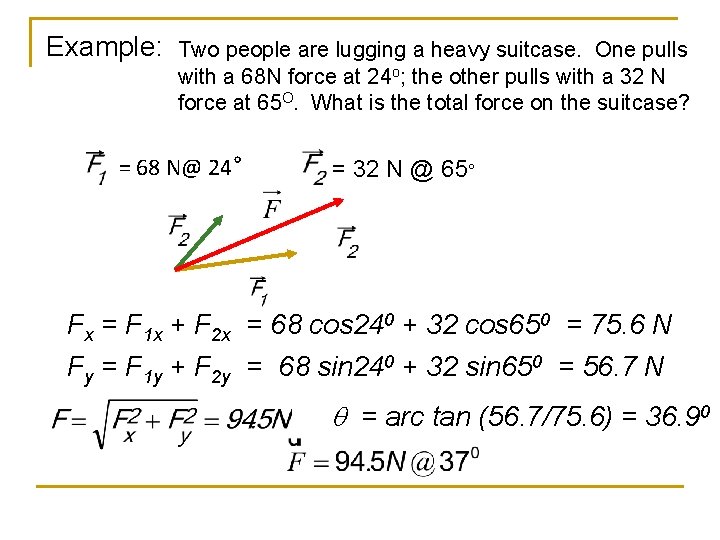
Example: Two people are lugging a heavy suitcase. One pulls with a 68 N force at 24 o; the other pulls with a 32 N force at 65 O. What is the total force on the suitcase? = 68 N@ 24° = 32 N @ 65° Solving procedure: 1) Move vectors head to tail. 2) Draw resultant. 3) Draw the x and y components of each vector. 4) Find Fx by adding F 1 x + F 2 x 5) Find Fy by adding F 1 y + F 2 y 6) Calculate F using Pythagorean theorem 7) Calculate q by using tan-1

Example: Two people are lugging a heavy suitcase. One pulls with a 68 N force at 24 o; the other pulls with a 32 N force at 65 O. What is the total force on the suitcase? = 68 N@ 24° = 32 N @ 65° Fx = F 1 x + F 2 x = 68 cos 240 + 32 cos 650 = 75. 6 N Fy = F 1 y + F 2 y = 68 sin 240 + 32 sin 650 = 56. 7 N = arc tan (56. 7/75. 6) = 36. 90

You try these individually V 1 = 35 m/s @ 28 degrees V 2 = 40 m/s @ 60 degrees Find V = V 1 + V 2 n X 1 = 4. 8 km @ 140 degrees X 2 = 5. 3 km @ 30 degrees Find X = X 1 + X 2 n HINT: If x or y components point in opposite directions, then subtract the smaller from the larger!

Closure, HW, Exit Ticket Closure: How did what we do today … … relate to our unit statement? … demonstrate LP traits? … relate to TOK? HW: See handout. HW Quiz next class, test in 2 classes! Exit ticket: See handout