Vector Analysis Physics 11 1 1 Vectors 5

Vector Analysis Physics – 11. 1. 1 Vectors

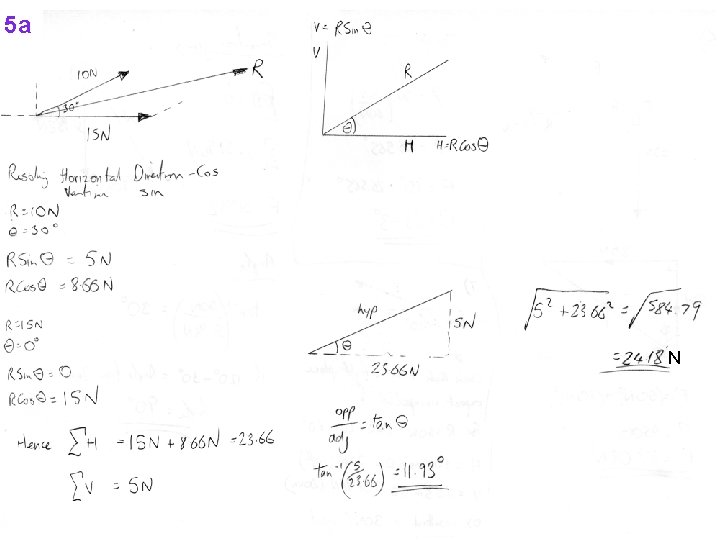
5 a N

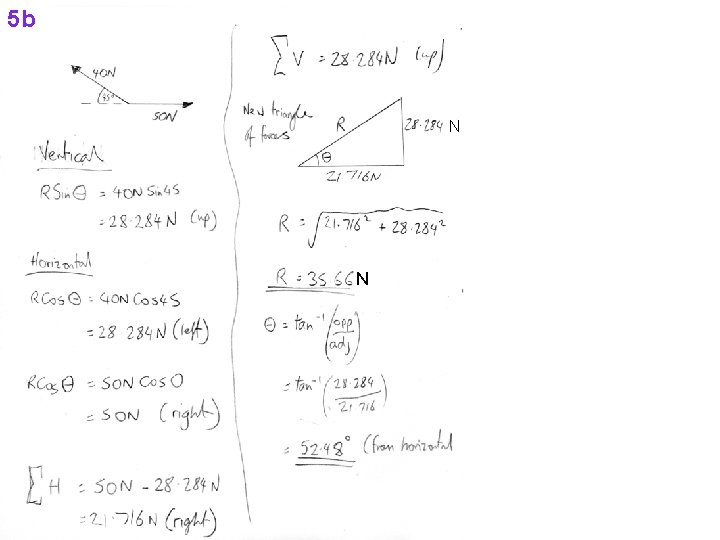
5 b N N

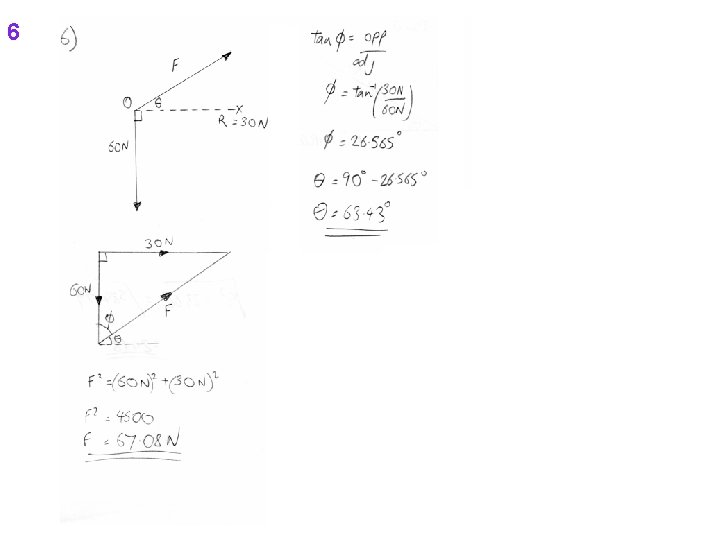
6

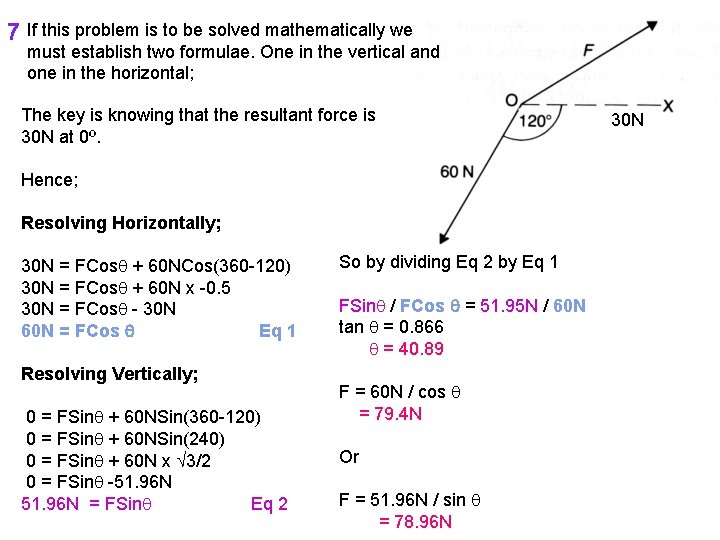
7 If this problem is to be solved mathematically we must establish two formulae. One in the vertical and one in the horizontal; The key is knowing that the resultant force is 30 N at 0º. Hence; Resolving Horizontally; 30 N = FCos + 60 NCos(360 -120) 30 N = FCos + 60 N x -0. 5 30 N = FCos - 30 N 60 N = FCos Eq 1 Resolving Vertically; 0 = FSin + 60 NSin(360 -120) 0 = FSin + 60 NSin(240) 0 = FSin + 60 N x 3/2 0 = FSin -51. 96 N = FSin Eq 2 So by dividing Eq 2 by Eq 1 FSin / FCos = 51. 95 N / 60 N tan = 0. 866 = 40. 89 F = 60 N / cos = 79. 4 N Or F = 51. 96 N / sin = 78. 96 N 30 N

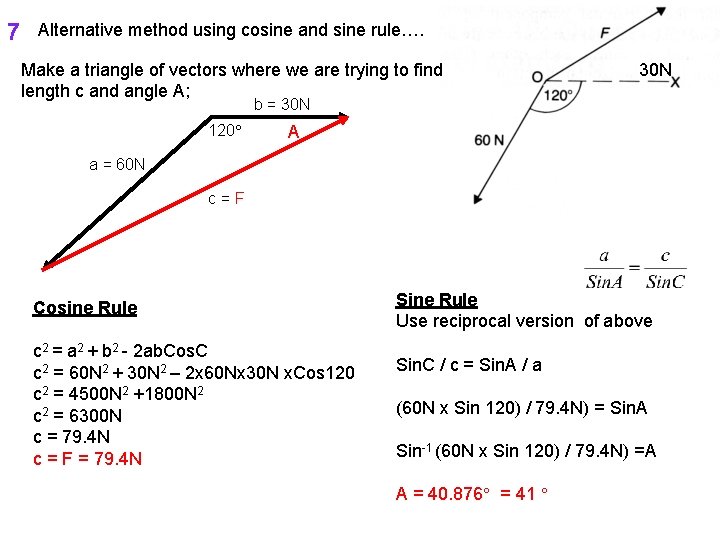
7 Alternative method using cosine and sine rule…. Make a triangle of vectors where we are trying to find length c and angle A; 30 N b = 30 N 120 A a = 60 N c=F Cosine Rule c 2 = a 2 + b 2 - 2 ab. Cos. C c 2 = 60 N 2 + 30 N 2 – 2 x 60 Nx 30 N x. Cos 120 c 2 = 4500 N 2 +1800 N 2 c 2 = 6300 N c = 79. 4 N c = F = 79. 4 N Sine Rule Use reciprocal version of above Sin. C / c = Sin. A / a (60 N x Sin 120) / 79. 4 N) = Sin. A Sin-1 (60 N x Sin 120) / 79. 4 N) =A A = 40. 876 = 41

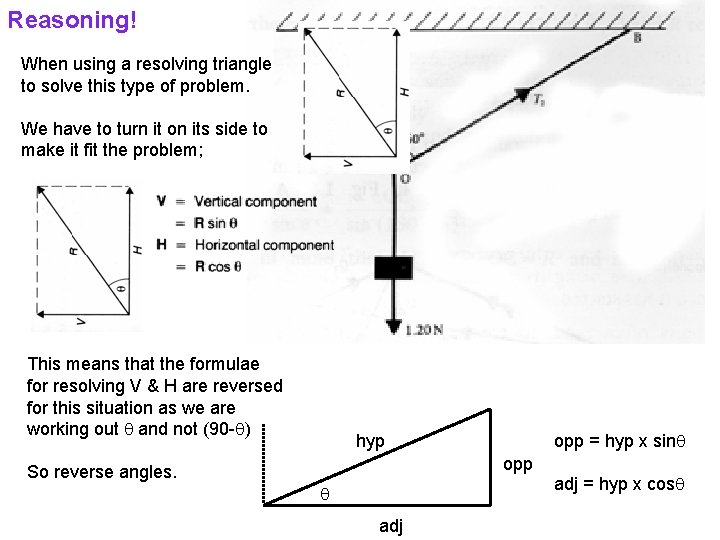
Reasoning! When using a resolving triangle to solve this type of problem. We have to turn it on its side to make it fit the problem; This means that the formulae for resolving V & H are reversed for this situation as we are working out and not (90 - ) So reverse angles. hyp opp = hyp x sin opp adj = hyp x cos adj

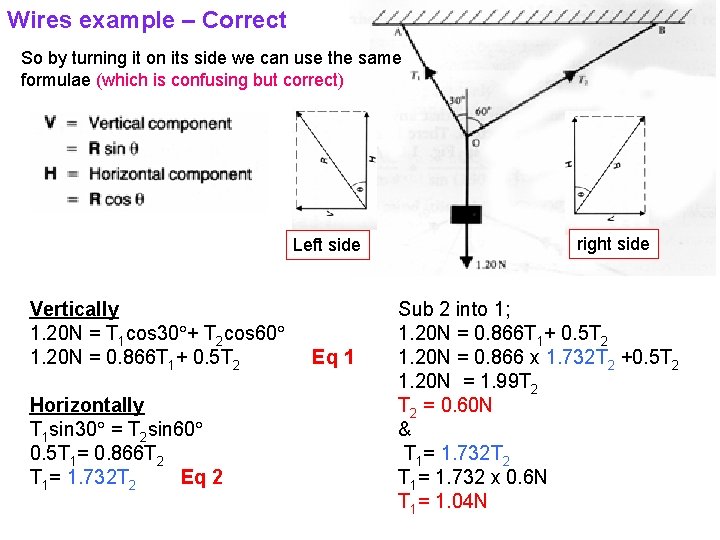
Wires example – Correct So by turning it on its side we can use the same formulae (which is confusing but correct) Left side Vertically 1. 20 N = T 1 cos 30 + T 2 cos 60 1. 20 N = 0. 866 T 1+ 0. 5 T 2 Horizontally T 1 sin 30 = T 2 sin 60 0. 5 T 1= 0. 866 T 2 T 1= 1. 732 T 2 Eq 1 right side Sub 2 into 1; 1. 20 N = 0. 866 T 1+ 0. 5 T 2 1. 20 N = 0. 866 x 1. 732 T 2 +0. 5 T 2 1. 20 N = 1. 99 T 2 = 0. 60 N & T 1= 1. 732 T 2 T 1= 1. 732 x 0. 6 N T 1= 1. 04 N

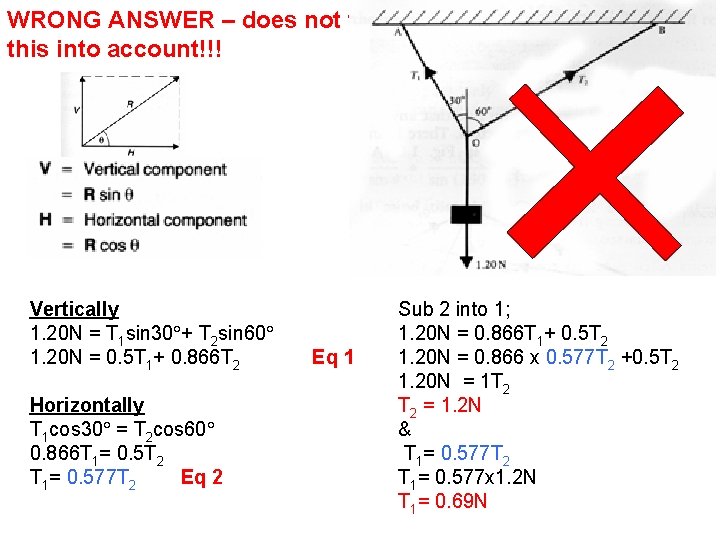
WRONG ANSWER – does not take this into account!!! Vertically 1. 20 N = T 1 sin 30 + T 2 sin 60 1. 20 N = 0. 5 T 1+ 0. 866 T 2 Horizontally T 1 cos 30 = T 2 cos 60 0. 866 T 1= 0. 5 T 2 T 1= 0. 577 T 2 Eq 1 Sub 2 into 1; 1. 20 N = 0. 866 T 1+ 0. 5 T 2 1. 20 N = 0. 866 x 0. 577 T 2 +0. 5 T 2 1. 20 N = 1 T 2 = 1. 2 N & T 1= 0. 577 T 2 T 1= 0. 577 x 1. 2 N T 1= 0. 69 N

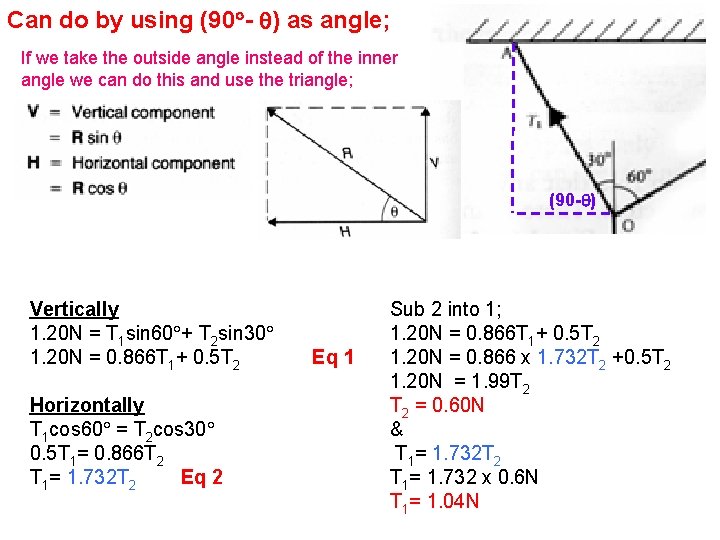
Can do by using (90 - ) as angle; If we take the outside angle instead of the inner angle we can do this and use the triangle; (90 - ) Vertically 1. 20 N = T 1 sin 60 + T 2 sin 30 1. 20 N = 0. 866 T 1+ 0. 5 T 2 Horizontally T 1 cos 60 = T 2 cos 30 0. 5 T 1= 0. 866 T 2 T 1= 1. 732 T 2 Eq 1 Sub 2 into 1; 1. 20 N = 0. 866 T 1+ 0. 5 T 2 1. 20 N = 0. 866 x 1. 732 T 2 +0. 5 T 2 1. 20 N = 1. 99 T 2 = 0. 60 N & T 1= 1. 732 T 2 T 1= 1. 732 x 0. 6 N T 1= 1. 04 N