Vector Addition Properties of Vectors Chapter 4 Section

Vector Addition Properties of Vectors Chapter 4 Section 1

Objectives Determine graphically the sum of the magnitudes of two or more vectors. Solve problems of relative velocity.

Magnitude Vectors have a size(magnitude) and direction For some vectors the magnitude is so useful it has been given its own name: Magnitude of velocity is speed. Magnitude of displacement is distance. Vectors also incorporate a direction and it is necessary to define the coordinate system to use them appropriately.

Representing Vector Quantities Graphical representation An arrow with a specified length and direction. This will be used when drawing vector diagrams. acceleration velocity displacement

Representing Vector Quantities Algebraic – An italicized letter in bold face type. Ex: Displacementd = 50 km SW 50 km is the magnitude SW is the direction

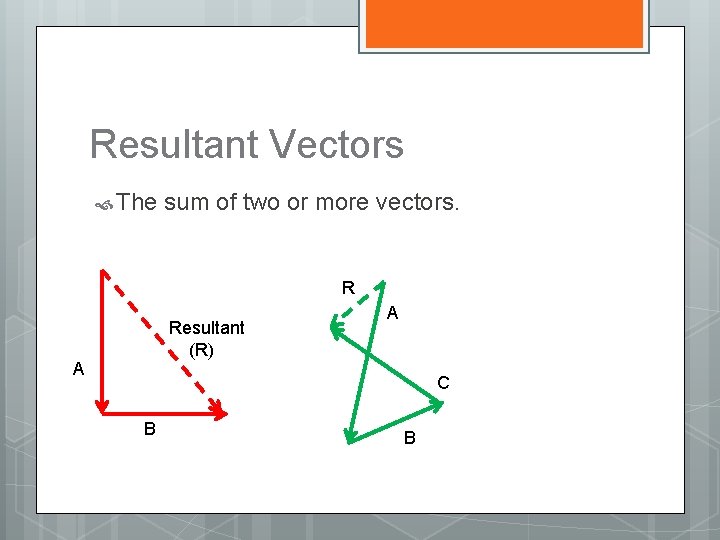
Resultant Vectors The sum of two or more vectors. R Resultant (R) A A C B B

Resultant Vectors If the two vectors being added are at right angles, then the magnitude can be found using the Pythagorean Theorem. R 2 = A 2 + B 2 R A B

Resultant Vectors If two vectors are at some angle other than 90 degrees, then use the Law of Cosines. B Θ A R 2 = A 2 + B 2 – 2 AB Cos Ө The vectors must be placed tail to tip and the angle Ө is the angle between them. R

Subtracting Vectors You can subtract vectors as well as add vectors. To subtract vectors remember the change in the vector rule: ∆V = V 2 - (V 1)

Relative Velocities Question! You’re in a school bus traveling at a velocity of 8 m/s in a positive direction. You walk at 3 m/s toward the front of the bus. How fast are you moving relative to the street? Graphical useful tool Vectors can be a

Relative Velocities Vbus relative to street Vyou relative to bus Vyou relative to street If you are walking inside the bus back to front and the bus is moving forwards, then add the two vectors.

Relative Velocities What about the reverse? Vbus relative to street Vyou relative to bus Vyou relative to street If you are walking inside the bus front to back (opposite the direction the bus is moving) then subtract the two vectors.