VDOE Mathematics Institute Grade Band 9 12 Functions

VDOE Mathematics Institute Grade Band 9 -12 Functions K-12 Mathematics Institutes Fall 2010

Placemat Consensus Functions Individual ideas are written here Common ideas are written here Individual ideas are written here Fall 2010 2

Overview of Vertical Progression Middle School (Function Analysis) 7. 12 … represent relationships with tables, graphs, rules and words 8. 14 … make connections between any two representations (tables, graphs, words, rules) Fall 2010 3

Overview of Vertical Progression Algebra I (Function Analysis) A. 7 The student will investigate and analyze function (linear and quadratic) families and their characteristics both algebraically and graphically, including a) determining whether a relation is a function; b) domain and range; c) zeros of a function; d) x- and y-intercepts; e) finding the values of a function for elements in its domain; and f) making connections between and among multiple representations of functions including concrete, verbal, numeric, graphic, and algebraic. Fall 2010 4

Overview of Vertical Progression Algebra, Functions and Data Analysis (Function Analysis) AFDA. 1 The student will investigate and analyze function (linear, quadratic, exponential, and logarithmic) families and their characteristics. Key concepts include a) continuity; b) local and absolute maxima and minima; c) domain and range; d) zeros; e) intercepts; f) intervals in which the function is increasing/decreasing; g) end behaviors; and h) asymptotes. Fall 2010 5

Overview of Vertical Progression Algebra, Functions and Data Analysis (Function Analysis) AFDA. 4 The student will transfer between and analyze multiple representations of functions, including algebraic formulas, graphs, tables, and words. Students will select and use appropriate representations for analysis, interpretation, and prediction. Fall 2010 6

Overview of Vertical Progression Algebra 2 (Function Analysis) AII. 7 The student will investigate and analyze functions algebraically and graphically. Key concepts include a) domain and range, including limited and discontinuous domains and ranges; b) zeros; c) x- and y-intercepts; d) intervals in which a function is increasing or decreasing; e) asymptotes; f) end behavior; g) inverse of a function; and h) composition of multiple functions. Graphing calculators will be used as a tool to assist in investigation of functions. Fall 2010 7

Vocabulary The new 2009 SOL mathematics standards focus on the use of appropriate and accurate mathematics vocabulary. Fall 2010 8

“Function” Vocabulary Across Grade Levels § § § § Fall 2010 Relation Domain – limited/ discontinuous Range Continuity Zeros Intercepts Elements (values) Multiple Representations § Local & Absolute Maxima & Minima (turning points) § Increasing/ Decreasing Intervals § End Behavior § Inverses § Asymptotes (and holes) 9

Vocabulary Across Grade Levels Evaluate Solve Simplify Apply Analyze Construct Fall 2010 Compare/contrast Calculate Graph Transform Factor Identify 10

Wordle – Algebra I 2009 VA SOLs www. wordle. net Fall 2010 11

Wordle – Algebra, Functions and Data Analysis 2009 VA SOLs Fall 2010 12

Wordle – Algebra II 2009 VA SOLs Fall 2010 13

Wordle – Algebra I, Algebra II, Algebra, Functions & Data Analysis, and Geometry Fall 2010 14

Reasoning with Functions Key elements of reasoning and sense making with functions include: • Using multiple representations of functions • Modeling by using families of functions • Analyzing the effects of different parameters Adapted from Focus in High School Mathematics: Reasoning and Sense Making, NCTM, 2009 Fall 2010 15

Using Multiple Representations of Functions • • Fall 2010 Tables Graphs or diagrams Symbolic representations Verbal descriptions 16

Algebra Tiles ~ Adding Add the polynomials. (x – 2) + (x + 1) = 2 x - 1 Fall 2010 17

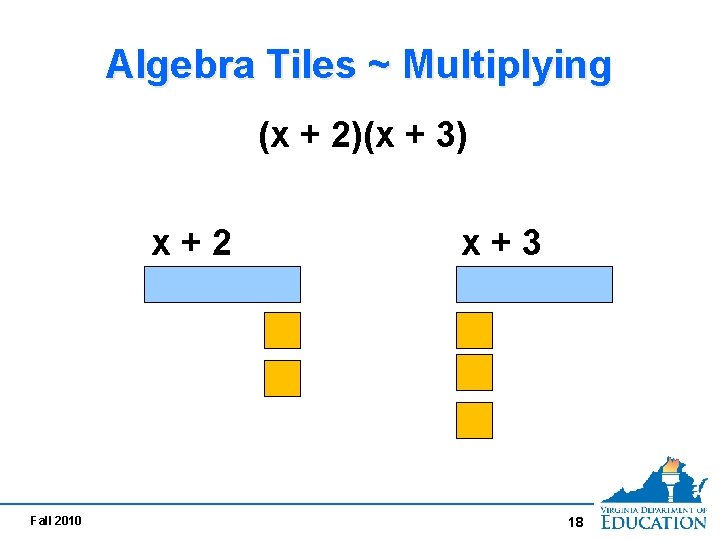
Algebra Tiles ~ Multiplying (x + 2)(x + 3) x+2 Fall 2010 x+3 18

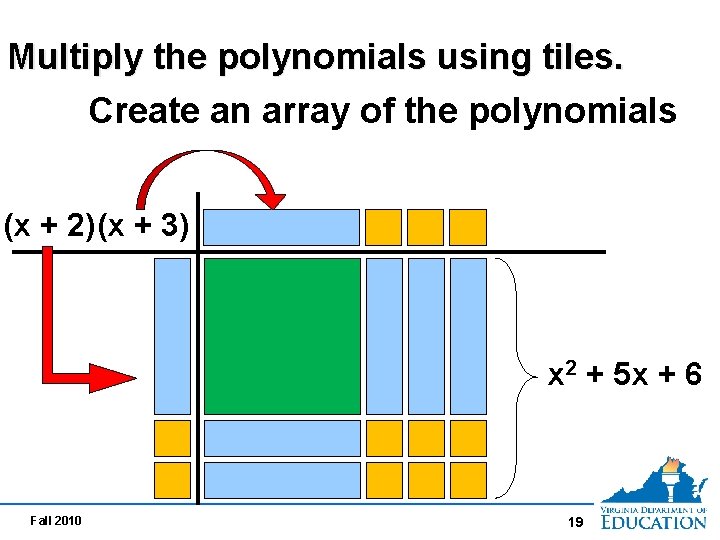
Multiply the polynomials using tiles. Create an array of the polynomials (x + 2)(x + 3) x 2 + 5 x + 6 Fall 2010 19

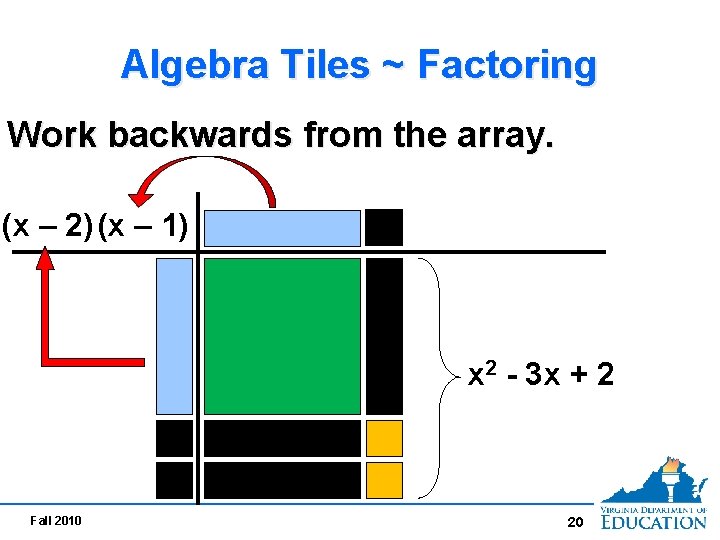
Algebra Tiles ~ Factoring Work backwards from the array. (x – 2) (x – 1) x 2 - 3 x + 2 Fall 2010 20

Polynomial Division A. 2 The student will perform operations on polynomials, including a)applying the laws of exponents to perform operations on expressions; b)adding, subtracting, multiplying, and dividing polynomials; and c)factoring completely first- and seconddegree binomials and trinomials in one or two variables. Graphing calculators will be used as a tool for factoring and for confirming algebraic factorizations. Fall 2010 21

Polynomial Division Divide (x 2 + 5 x + 6) by (x + 3) Common factors only will be used……no long division! Let’s look at division using Algebra Tiles Fall 2010 22

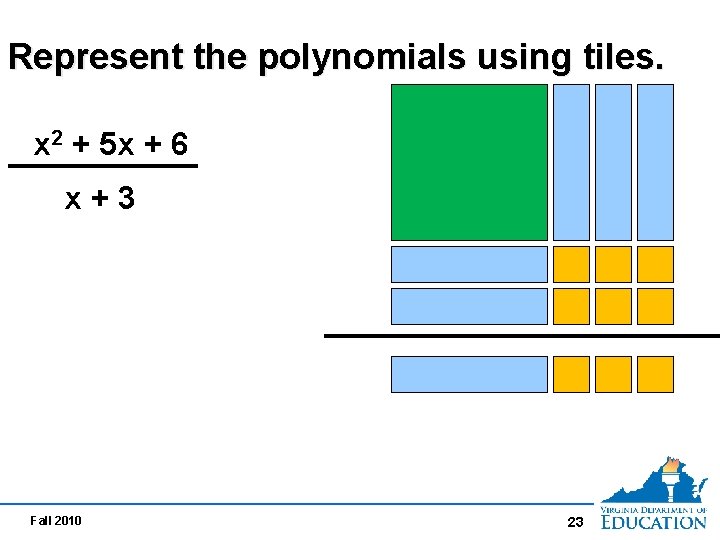
Represent the polynomials using tiles. x 2 + 5 x + 6 x+3 Fall 2010 23

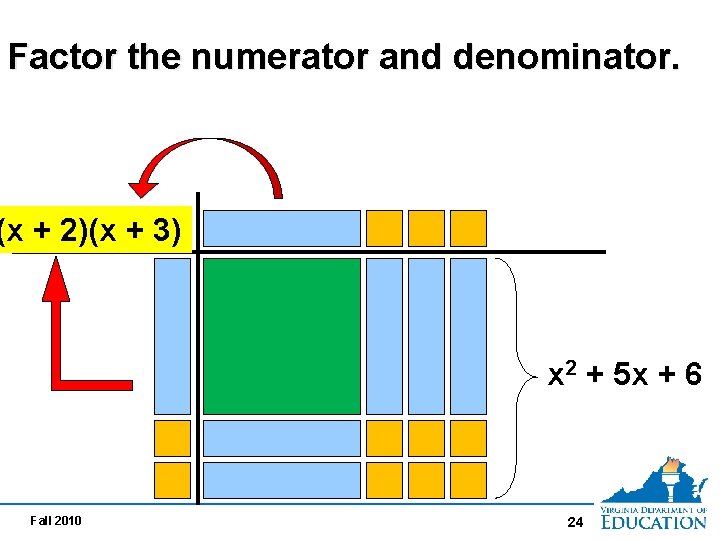
Factor the numerator and denominator. (x ++ 2)(x++3) 3) (x x 2 + 5 x + 6 Fall 2010 24

Represent the polynomials using tiles. 2 + (xx+ 2)(x 5 x + 3) 6 (x + 3) Reduce fraction by simplifying like factors to equal 1. Fall 2010 x + 2 is the answer 25

Points of Interest for A. 2 from the Curriculum Framework Operations with polynomials can be represented concretely, pictorially, and symbolically. VDOE Algeblocks Training Video http: //www. vdoe. whro. org/A_Blocks 05/index. html Fall 2010 26

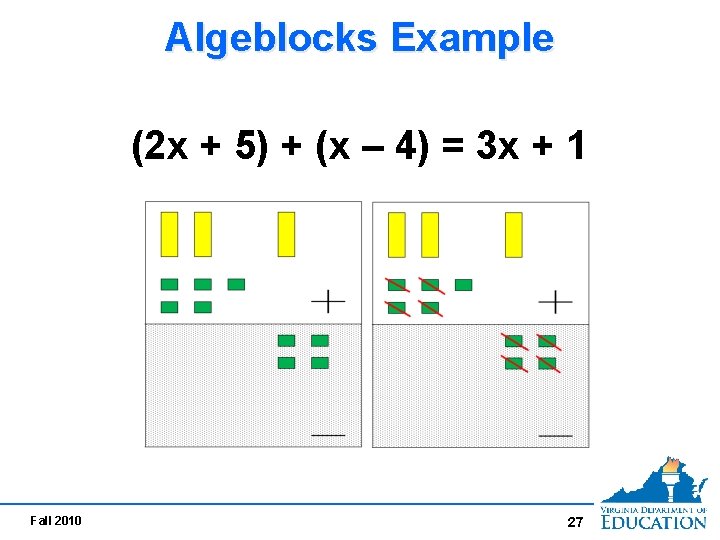
Algeblocks Example (2 x + 5) + (x – 4) = 3 x + 1 Fall 2010 27

Modeling by Using Families of Functions • Recognize the characteristics of different families of functions • Recognize the common features of each function family • Recognize how different data patterns can be modeled using each family Fall 2010 28

Analyzing the Effects of Parameters • Different, but equivalent algebraic expressions can be used to define the same function • Writing functions in different forms helps identify features of the function • Graphical transformations can be observed by changes in parameters Fall 2010 29

Overview of Functions Looking at Patterns Time vs. Distance Graphs allow students to relate observable patterns in one real world variable (distance) in terms of another real world variable (time). Fall 2010 30

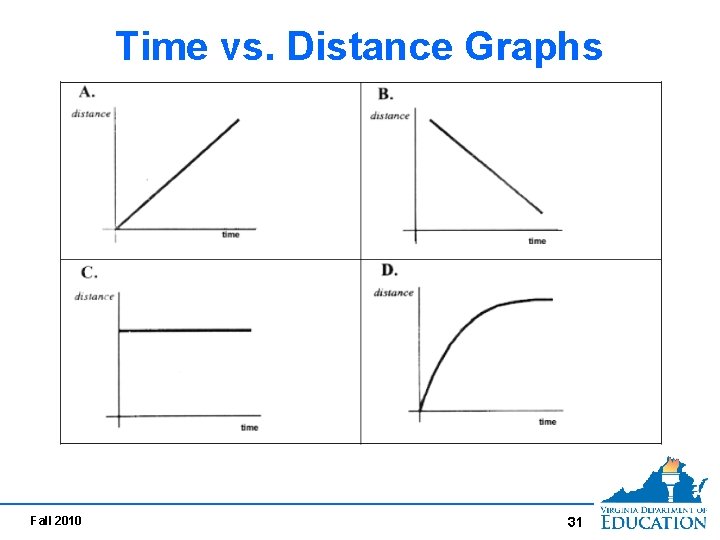
Time vs. Distance Graphs Fall 2010 31

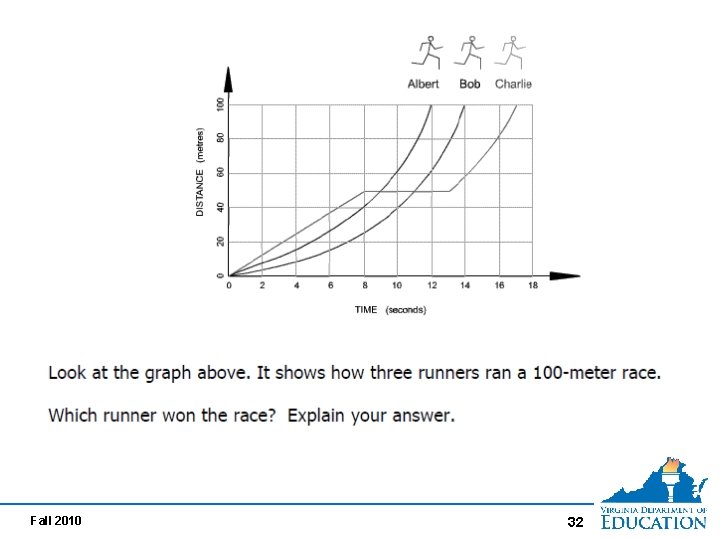
Fall 2010 32

Slope and Linear Functions • Students can begin to conceptualize slope and look at multiple representations of the same relationship given real world data, tables and graphs. Fall 2010 33

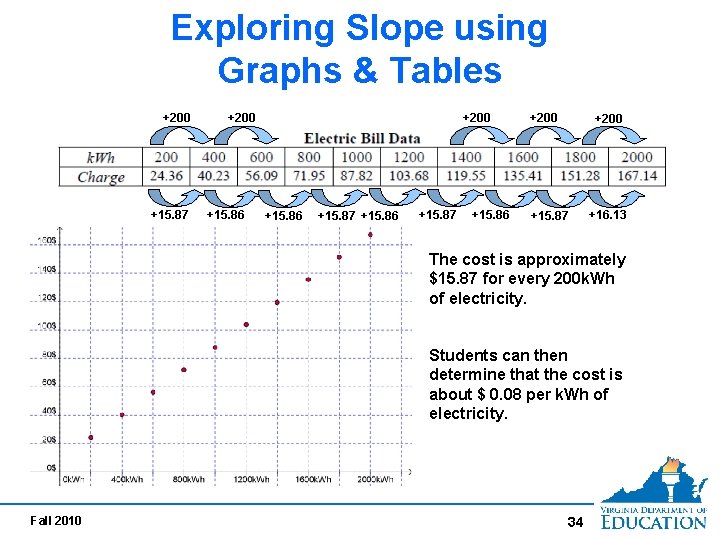
Exploring Slope using Graphs & Tables +200 +15. 87 +200 +15. 86 +15. 87 +15. 86 +200 +16. 13 +15. 87 The cost is approximately $15. 87 for every 200 k. Wh of electricity. Students can then determine that the cost is about $ 0. 08 per k. Wh of electricity. Fall 2010 34

Exploring Functions As students progress through high school mathematics, the concept of a function and its characteristics become more complex. Exploring families of functions allow students to compare and contrast the attributes of various functions. Fall 2010 35

Function Families Linear: Fall 2010 Absolute Value: 36

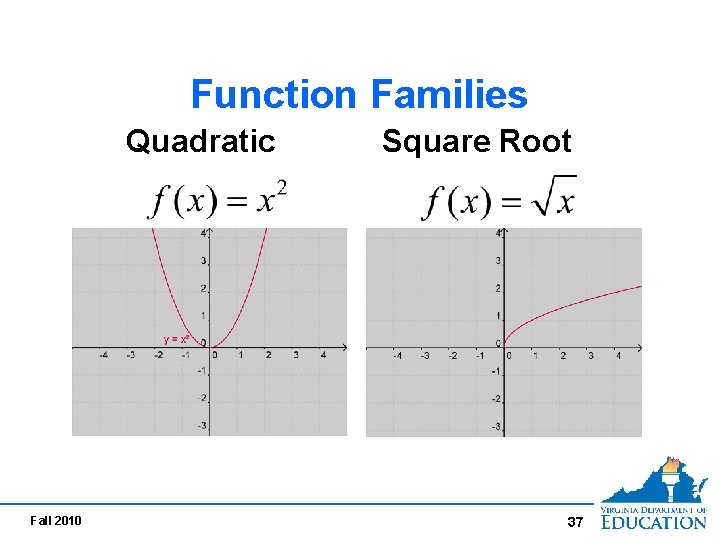
Function Families Quadratic Fall 2010 Square Root 37

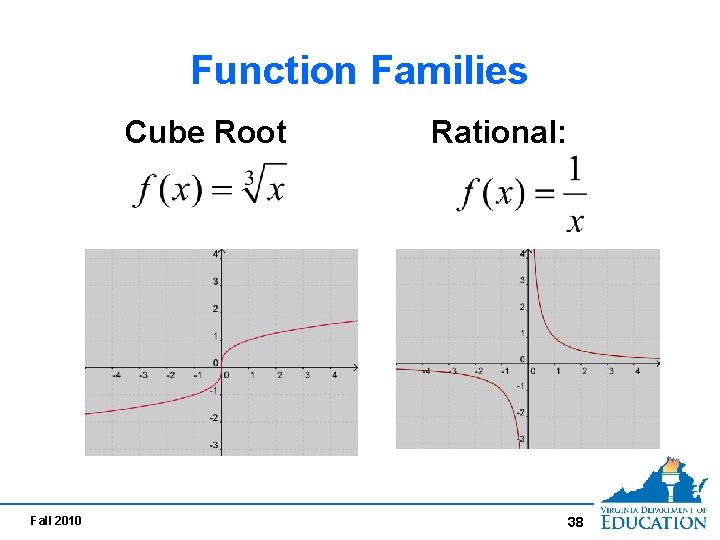
Function Families Cube Root Fall 2010 Rational: 38

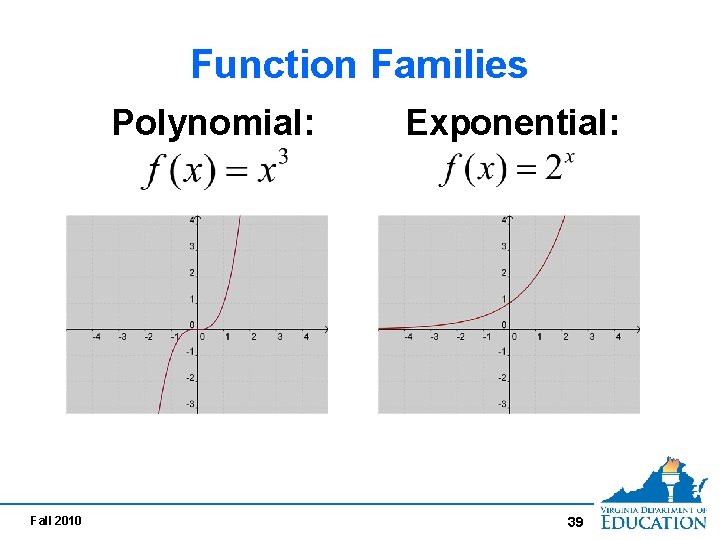
Function Families Polynomial: Fall 2010 Exponential: 39

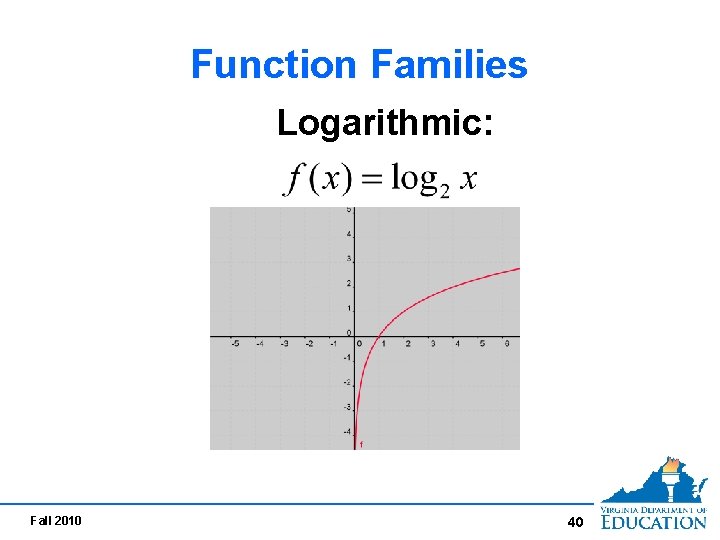
Function Families Logarithmic: Fall 2010 40

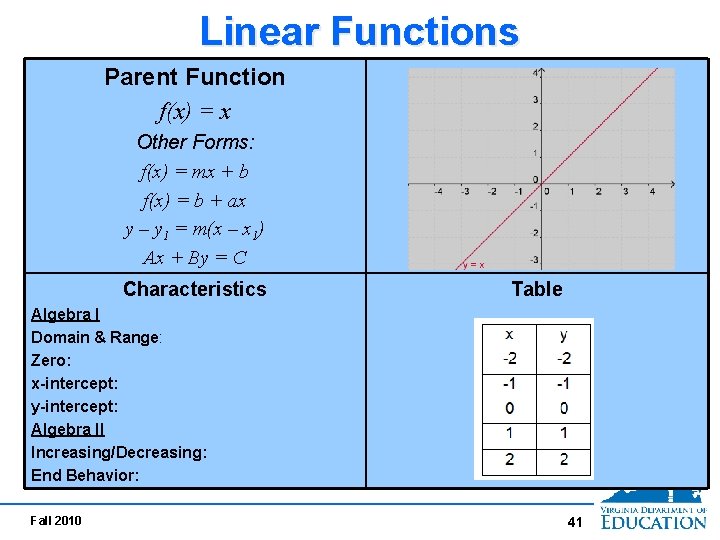
Linear Functions Parent Function f(x) = x Other Forms: f(x) = mx + b f(x) = b + ax y – y 1 = m(x – x 1) Ax + By = C Characteristics Table Algebra I Domain & Range: Zero: x-intercept: y-intercept: Algebra II Increasing/Decreasing: End Behavior: Fall 2010 41

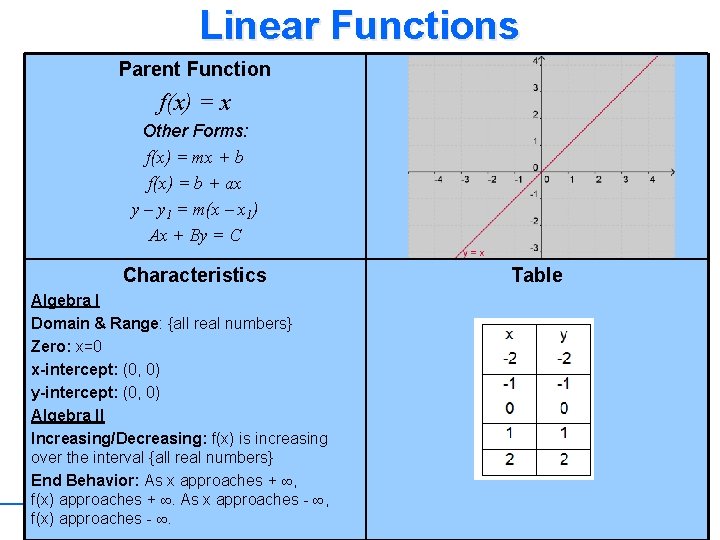
Linear Functions Parent Function f(x) = x Other Forms: f(x) = mx + b f(x) = b + ax y – y 1 = m(x – x 1) Ax + By = C Characteristics Algebra I Domain & Range: {all real numbers} Zero: x=0 x-intercept: (0, 0) y-intercept: (0, 0) Algebra II Increasing/Decreasing: f(x) is increasing over the interval {all real numbers} End Behavior: As x approaches + ∞, f(x) approaches + ∞. As x approaches - ∞, f(x) approaches - ∞. Fall 2010 Table 42

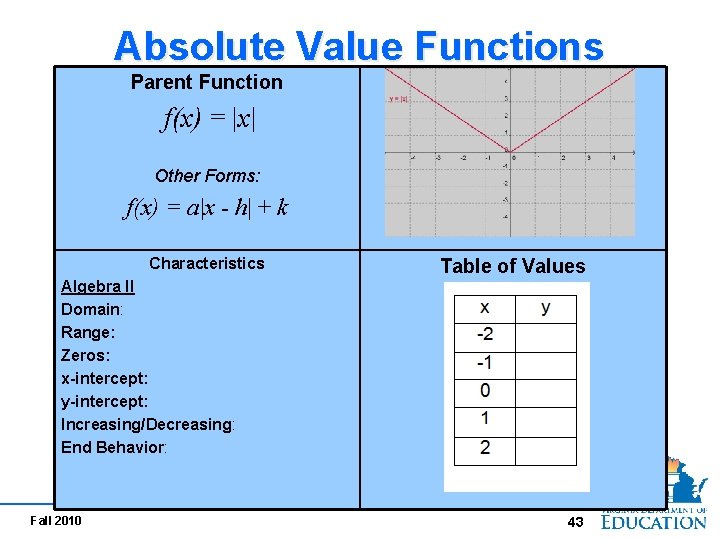
Absolute Value Functions Parent Function f(x) = |x| Other Forms: f(x) = a|x - h| + k Characteristics Table of Values Algebra II Domain: Range: Zeros: x-intercept: y-intercept: Increasing/Decreasing: End Behavior: Fall 2010 43

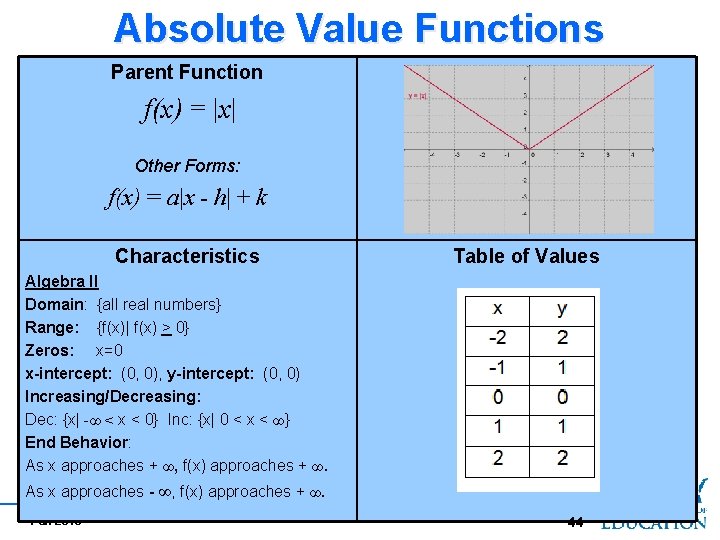
Absolute Value Functions Parent Function f(x) = |x| Other Forms: f(x) = a|x - h| + k Characteristics Table of Values Algebra II Domain: {all real numbers} Range: {f(x)| f(x) > 0} Zeros: x=0 x-intercept: (0, 0), y-intercept: (0, 0) Increasing/Decreasing: Dec: {x| -∞ < x < 0} Inc: {x| 0 < x < ∞} End Behavior: As x approaches + ∞, f(x) approaches + ∞. As x approaches - ∞, f(x) approaches + ∞. Fall 2010 44

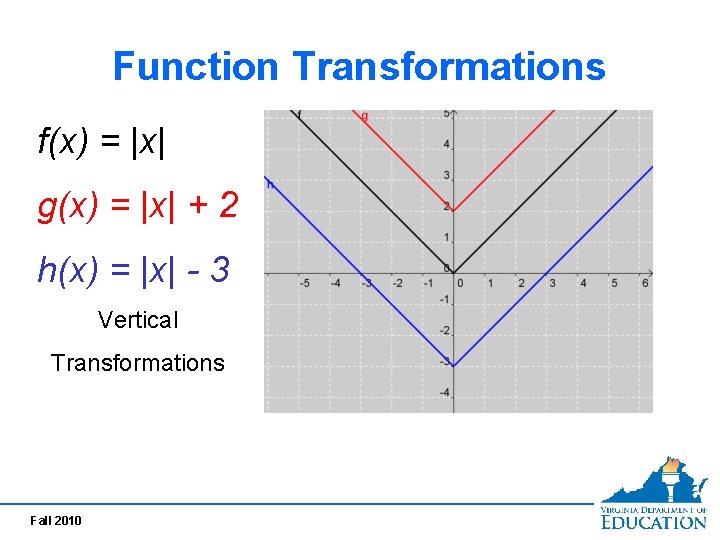
Function Transformations f(x) = |x| g(x) = |x| + 2 h(x) = |x| - 3 Vertical Transformations Fall 2010

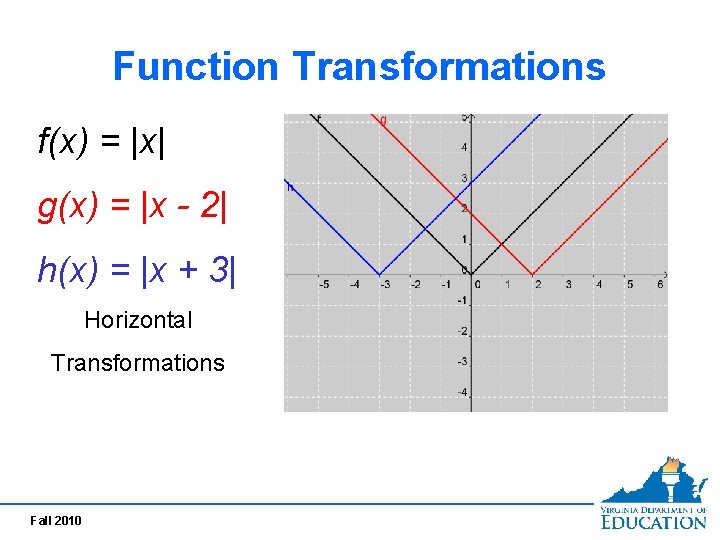
Function Transformations f(x) = |x| g(x) = |x - 2| h(x) = |x + 3| Horizontal Transformations Fall 2010

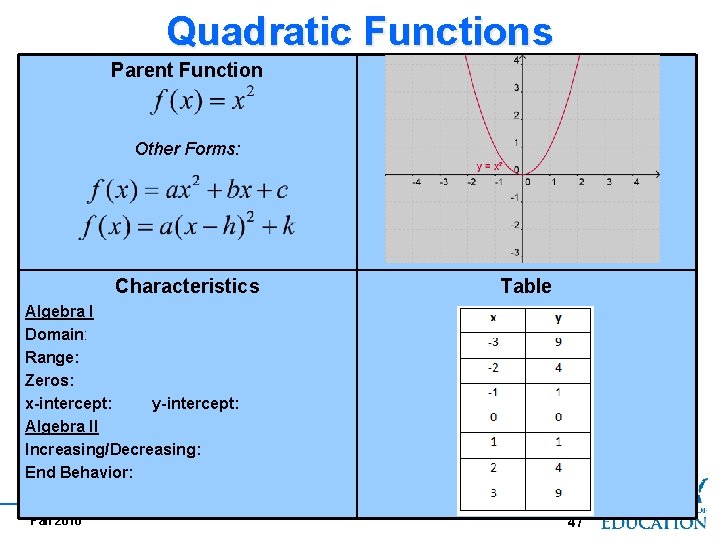
Quadratic Functions Parent Function Other Forms: Characteristics Table Algebra I Domain: Range: Zeros: x-intercept: y-intercept: Algebra II Increasing/Decreasing: End Behavior: 47 Fall 2010 47

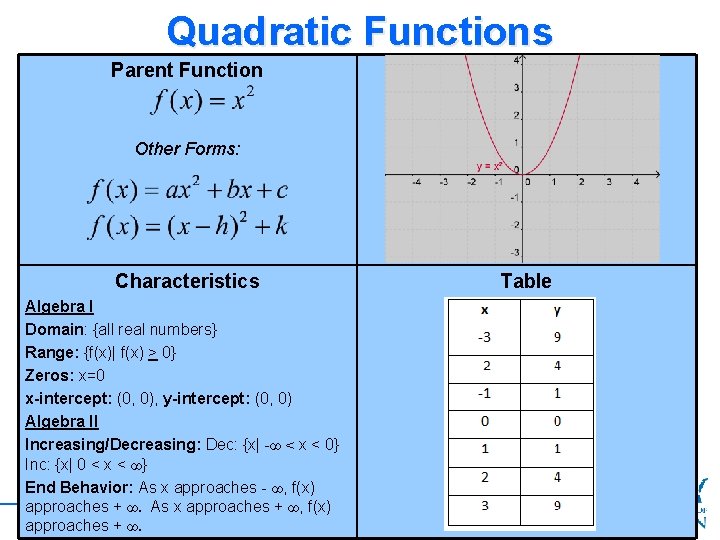
Quadratic Functions Parent Function Other Forms: Characteristics Algebra I Domain: {all real numbers} Range: {f(x)| f(x) > 0} Zeros: x=0 x-intercept: (0, 0), y-intercept: (0, 0) Algebra II Increasing/Decreasing: Dec: {x| -∞ < x < 0} Inc: {x| 0 < x < ∞} End Behavior: As x approaches - ∞, f(x) approaches + ∞. As x approaches + ∞, f(x) Fall 2010 approaches + ∞. Table 48

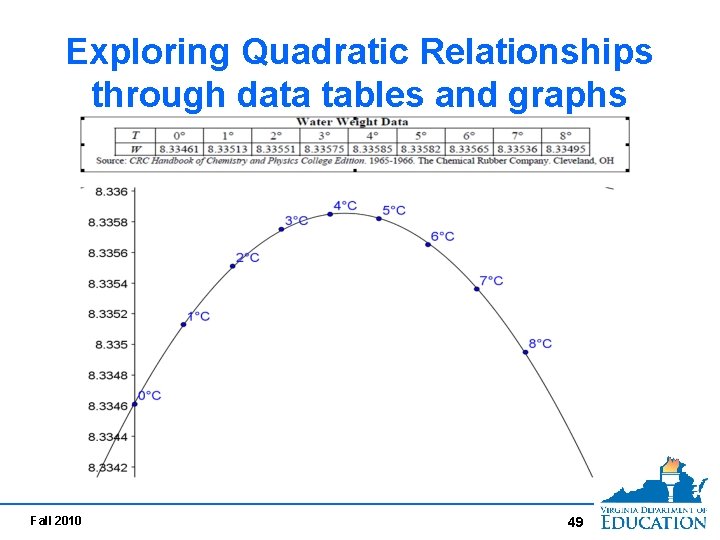
Exploring Quadratic Relationships through data tables and graphs Fall 2010 49

TAKE a BREAK Fall 2010

Square Root Functions Parent Function Other Forms: Characteristics Table Algebra II Domain: Range: Zeros: x-intercept: y-intercept: Increasing/Decreasing: End Behavior: 51 Fall 2010 51

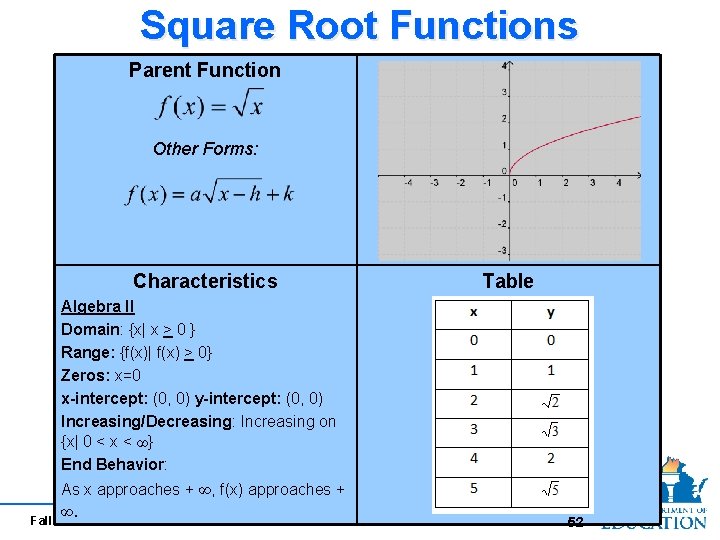
Square Root Functions Parent Function Other Forms: Characteristics Table Algebra II Domain: {x| x > 0 } Range: {f(x)| f(x) > 0} Zeros: x=0 x-intercept: (0, 0) y-intercept: (0, 0) Increasing/Decreasing: Increasing on {x| 0 < x < ∞} End Behavior: As x approaches + ∞, f(x) approaches + ∞. Fall 2010 52 52

Square Root Function Real World Application The speed of a tsunami is a function of ocean depth: SPEED = g = acceleration due to gravity (9. 81 m/s 2) d = depth of the ocean in meters Understanding the speed of tsunamis is useful in issuing warnings to coastal regions. Knowing the speed can help predict when the tsunami will arrive at a particular location. Fall 2010 53

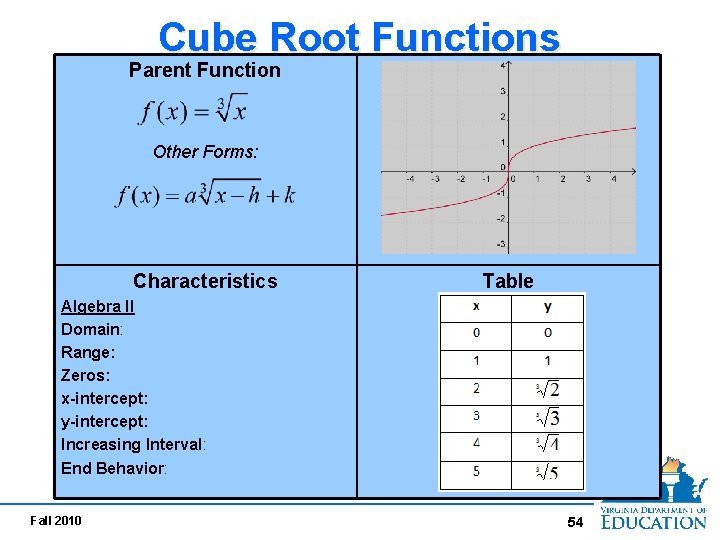
Cube Root Functions Parent Function Other Forms: Characteristics Table Algebra II Domain: Range: Zeros: x-intercept: y-intercept: Increasing Interval: End Behavior: 54 Fall 2010 54

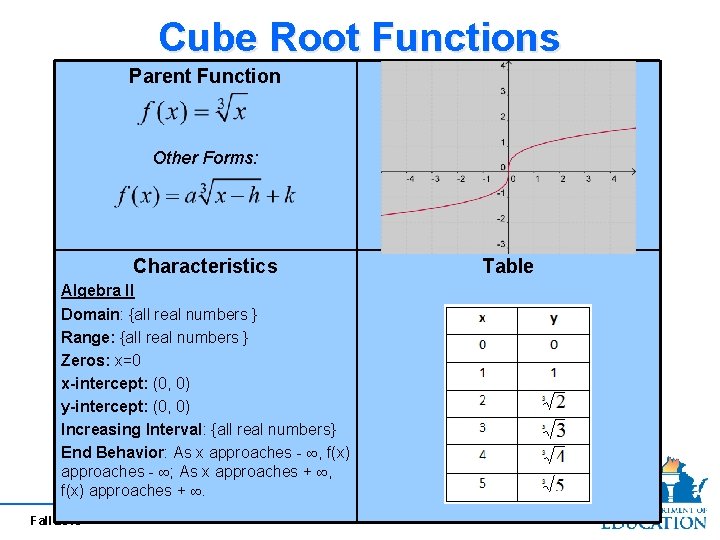
Cube Root Functions Parent Function Other Forms: Characteristics Algebra II Domain: {all real numbers } Range: {all real numbers } Zeros: x=0 x-intercept: (0, 0) y-intercept: (0, 0) Increasing Interval: {all real numbers} End Behavior: As x approaches - ∞, f(x) approaches - ∞; As x approaches + ∞, f(x) approaches + ∞. Fall 2010 Table 55

Cube Root Function Real World Application Kepler’s Law of Planetary Motion: The distance, d, of a planet from the Sun in millions of miles is equal to the cube root of 6 times the number of Earth days it takes for the planet to orbit the sun, squared. For example, the length of a year on Mars is 687 Earth-days. Thus, d = 141. 478 million miles from the Sun Fall 2010 56

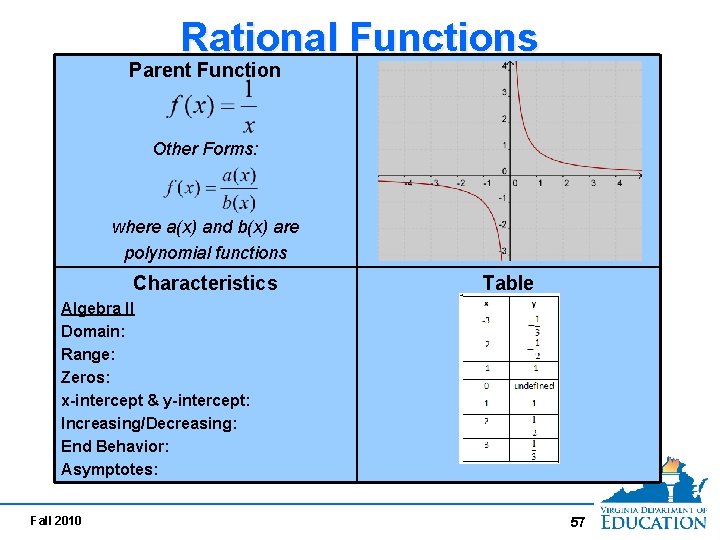
Rational Functions Parent Function Other Forms: where a(x) and b(x) are polynomial functions Characteristics Table Algebra II Domain: Range: Zeros: x-intercept & y-intercept: Increasing/Decreasing: End Behavior: Asymptotes: Fall 2010 57

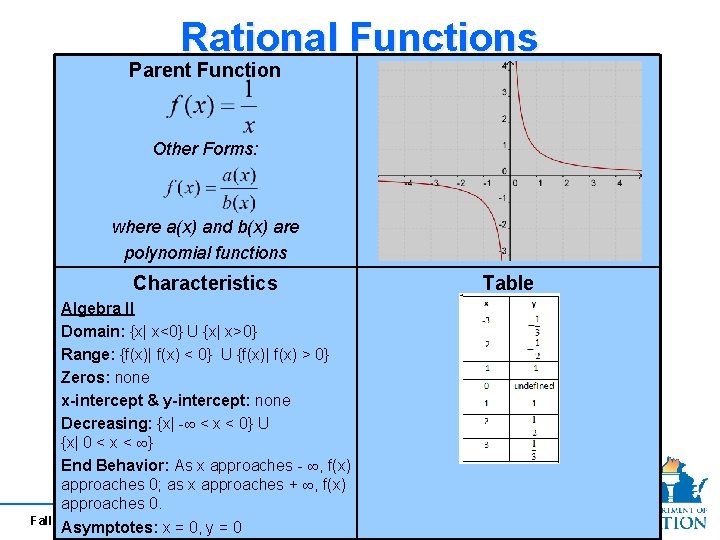
Rational Functions Parent Function Other Forms: where a(x) and b(x) are polynomial functions Characteristics Algebra II Domain: {x| x<0} U {x| x>0} Range: {f(x)| f(x) < 0} U {f(x)| f(x) > 0} Zeros: none x-intercept & y-intercept: none Decreasing: {x| -∞ < x < 0} U {x| 0 < x < ∞} End Behavior: As x approaches - ∞, f(x) approaches 0; as x approaches + ∞, f(x) approaches 0. Fall 2010 Asymptotes: x = 0, y = 0 Table 58

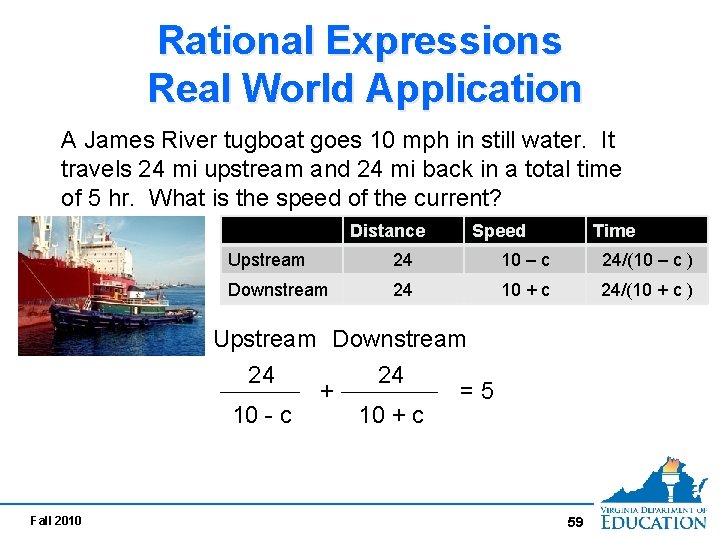
Rational Expressions Real World Application A James River tugboat goes 10 mph in still water. It travels 24 mi upstream and 24 mi back in a total time of 5 hr. What is the speed of the current? Distance Speed Time Upstream 24 10 – c 24/(10 t 1 – c ) Downstream 24 10 + c 24/(10 t 2 + c ) Upstream Downstream 24 10 - c Fall 2010 + 24 10 + c =5 59

Rational Expressions Real World Application (10 – c) (10 + c) 24 10 - c + 24 10 + c =5 (10 – c) (10 + c) 24(10 + c) + 24 (10 – c) = 5 (100 – c 2) 480 = 500 - 5 c 2 - 20 = 0 5(c + 2)(c – 2) = 0 c = 2 or -2 The speed of the current is 2 mph. Fall 2010 60

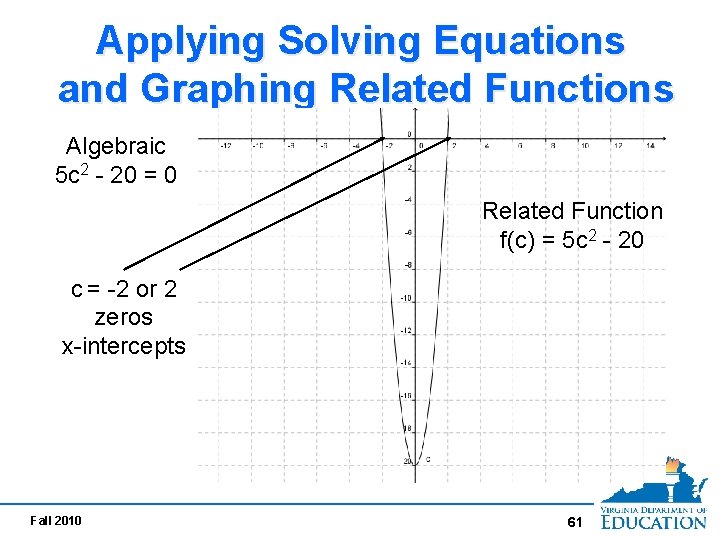
Applying Solving Equations and Graphing Related Functions Algebraic 5 c 2 - 20 = 0 Related Function f(c) = 5 c 2 - 20 c = -2 or 2 zeros x-intercepts Fall 2010 61

Solving Equations & Functions A. 4 The student will solve multistep linear and quadratic equations in two variables…. . Framework Identify the root(s) or zero(s) of a …. . function over the real number system as the solution(s) to the …. . equation that is formed by setting the given …… expression equal to zero. Fall 2010 62

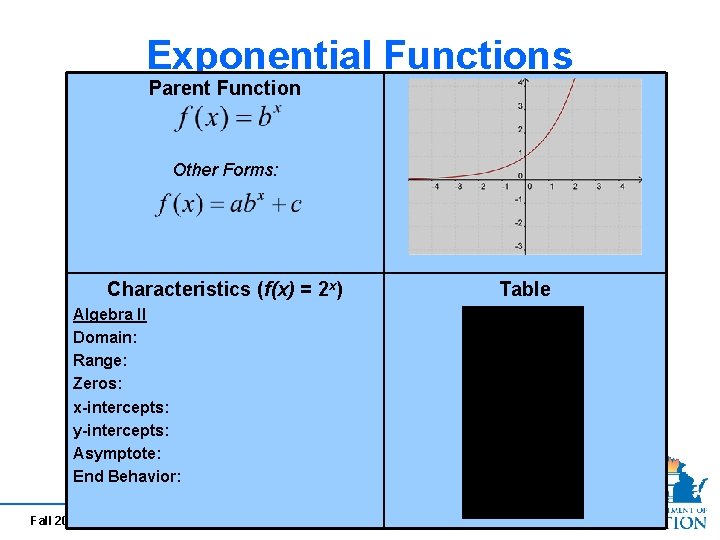
Exponential Functions Parent Function Other Forms: Characteristics (f(x) = 2 x) Algebra II Domain: Range: Zeros: x-intercepts: y-intercepts: Asymptote: End Behavior: Fall 2010 Table

Exponential Functions Parent Function Other Forms: Characteristics (f(x) = 2 x) Algebra II Domain: {all real numbers} Range: {f(x)| f(x) > 0} Zeros: none x-intercepts: none y-intercepts: (0, 1) Asymptote: y = 0 End Behavior: As x approaches ∞, f(x) approaches + ∞. As x approaches - ∞, f(x) approaches 0. Fall 2010 Table

Exponential Function Real World Application Homemade chocolate chip cookies can lose their freshness over time. When the cookies are fresh, the taste quality is 1. The taste quality decreases according to the function: f(x) = 0. 8 x, where x represents the number of days since the cookies were baked and f(x) measures the taste quality. When will the cookies taste half as good as when they were fresh? 0. 5 = 0. 8 x log 0. 5 = x log 0. 8 x = log 0. 5 ÷ log 0. 8 x = 3 days Fall 2010 65

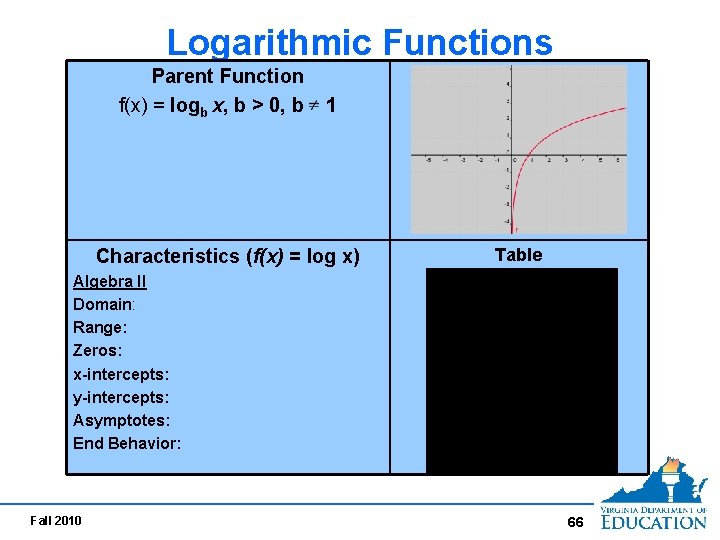
Logarithmic Functions Parent Function f(x) = logb x, b > 0, b 1 Characteristics (f(x) = log x) Table Algebra II Domain: Range: Zeros: x-intercepts: y-intercepts: Asymptotes: End Behavior: Fall 2010 66

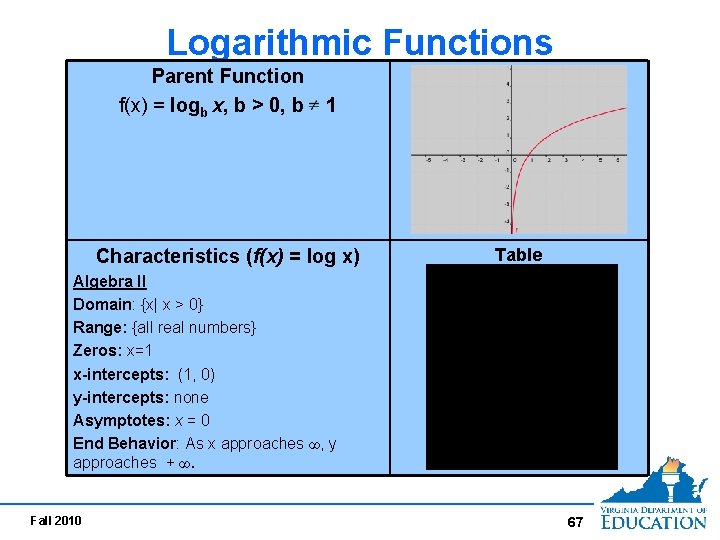
Logarithmic Functions Parent Function f(x) = logb x, b > 0, b 1 Characteristics (f(x) = log x) Table Algebra II Domain: {x| x > 0} Range: {all real numbers} Zeros: x=1 x-intercepts: (1, 0) y-intercepts: none Asymptotes: x = 0 End Behavior: As x approaches ∞, y approaches + ∞. Fall 2010 67

Logarithmic Function Real World Application The wind speed, s (in miles per hour), near the center of a tornado can be modeled by s = 93 log d + 65 Where d is the distance (in miles) that the tornado travels. In 1925, a tornado traveled 220 miles through three states. Estimate the wind speed near the tornado’s center. s = 93 log d + 65 s = 93 log 220 + 65 s = 93(2. 342) + 65 s = 282. 806 miles/hour Fall 2010 68

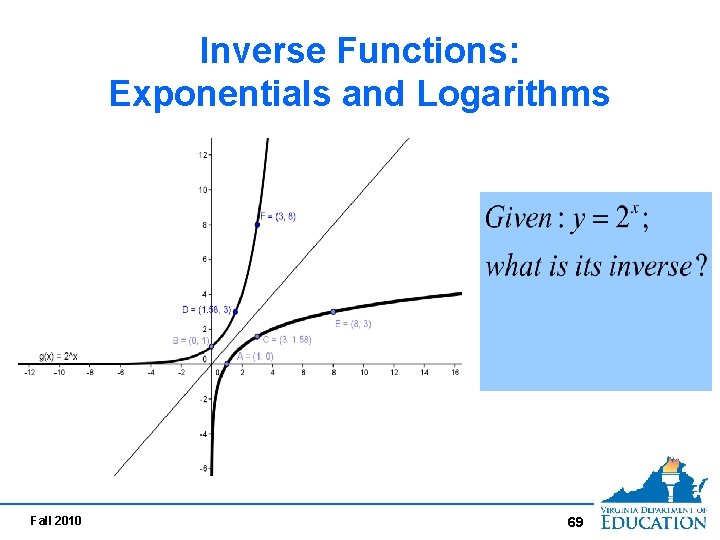
Inverse Functions: Exponentials and Logarithms Fall 2010 69

Functions and Inverses Every function has an inverse relation, but not Function every inverse relation is a function. Not a Function When is a function invertible? A function is invertible if its inverse relation is also a function. Fall 2010 70

Quadratic Functions Require Restricted Domains in order to be Invertible Function: Inverse Function: Fall 2010 x f(x) 0 0 1 1 2 4 3 9 x f -1(x) 0 0 1 1 4 2 9 3 71

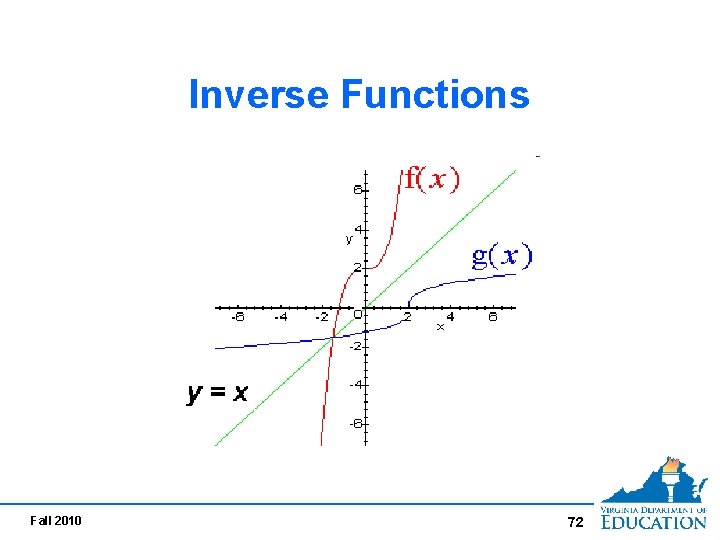
Inverse Functions Fall 2010 72

Polynomial Functions End behavior ~ direction of the ends of the graph Even Degree Same directions Odd Degree Opposite directions Fall 2010 Teachers should facilitate students’ generalizations 73

Real World Application Polynomial Function Suppose an object moves in a straight line so that its distance s(t) after t seconds, is represented by s(t)= t 3 + t 2 + 6 t feet from its starting point. Determine the distance traveled in the first 4 seconds. Fall 2010 74

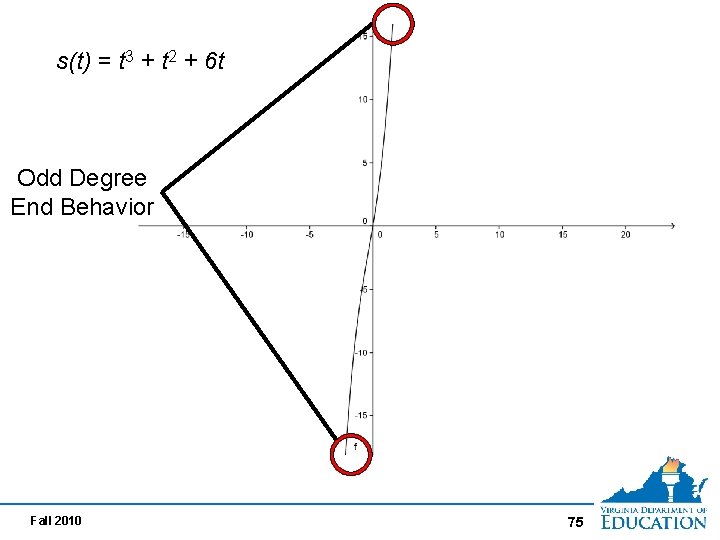
s(t) = t 3 + t 2 + 6 t Odd Degree End Behavior Fall 2010 75

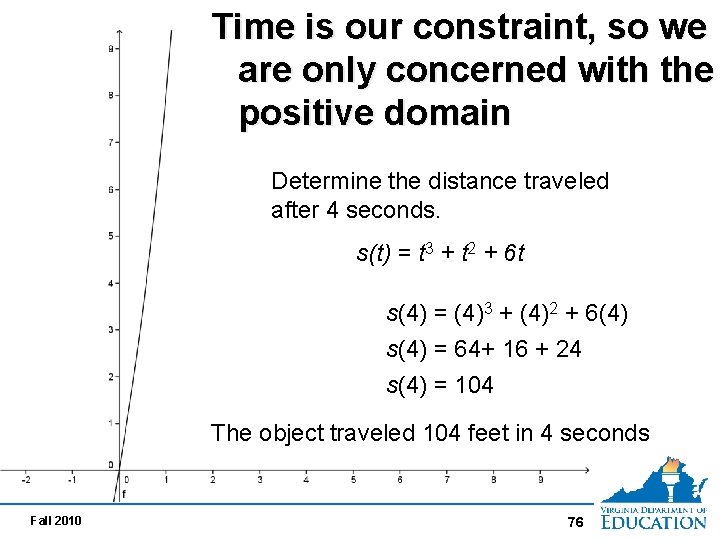
Time is our constraint, so we are only concerned with the positive domain Determine the distance traveled after 4 seconds. s(t) = t 3 + t 2 + 6 t s(4) = (4)3 + (4)2 + 6(4) s(4) = 64+ 16 + 24 s(4) = 104 The object traveled 104 feet in 4 seconds Fall 2010 76

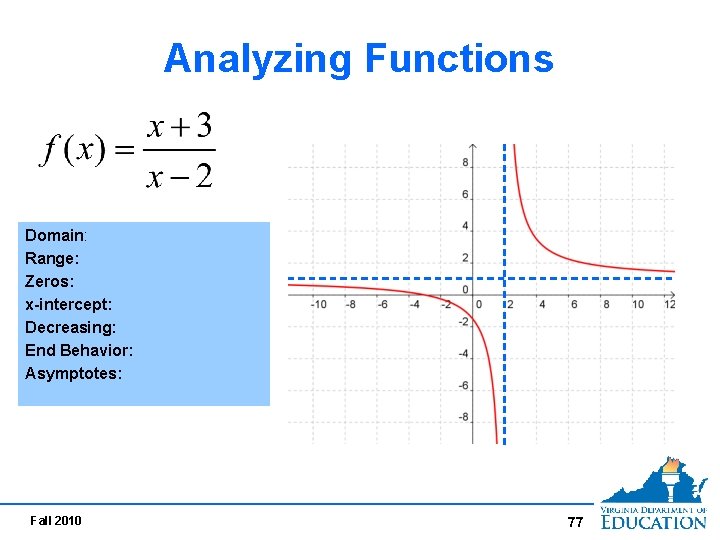
Analyzing Functions Domain: Range: Zeros: x-intercept: Decreasing: End Behavior: Asymptotes: Fall 2010 77

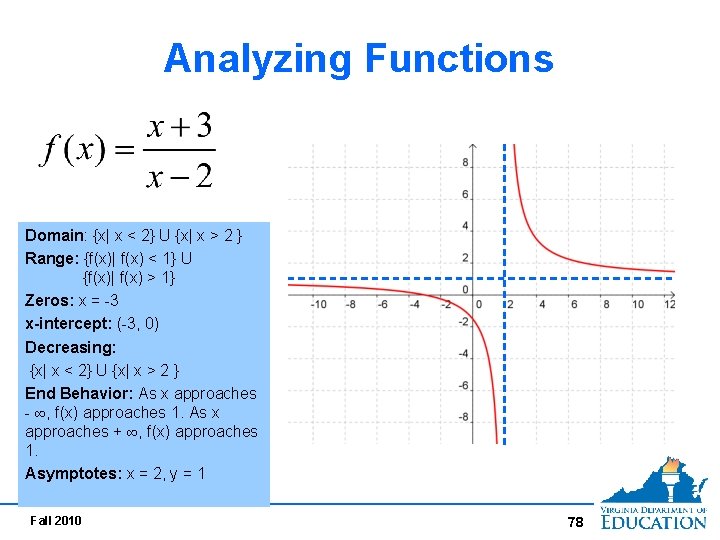
Analyzing Functions Domain: {x| x < 2} U {x| x > 2 } Range: {f(x)| f(x) < 1} U {f(x)| f(x) > 1} Zeros: x = -3 x-intercept: (-3, 0) Decreasing: {x| x < 2} U {x| x > 2 } End Behavior: As x approaches - ∞, f(x) approaches 1. As x approaches + ∞, f(x) approaches 1. Asymptotes: x = 2, y = 1 Fall 2010 78

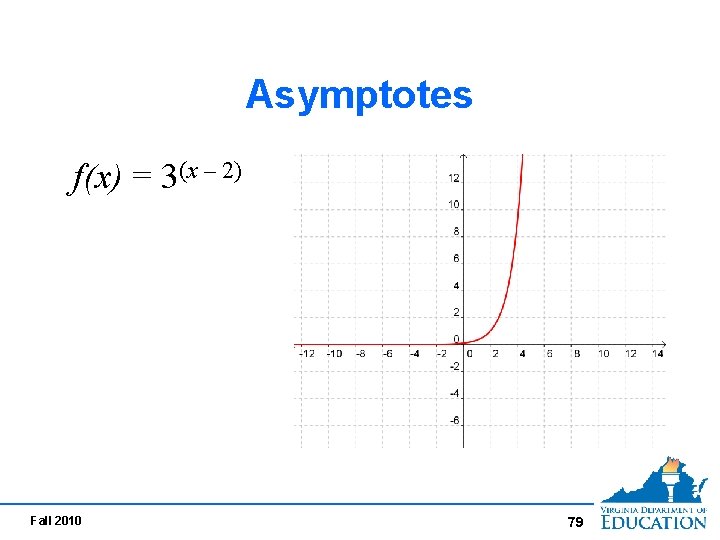
Asymptotes f(x) = 3(x – 2) Fall 2010 79

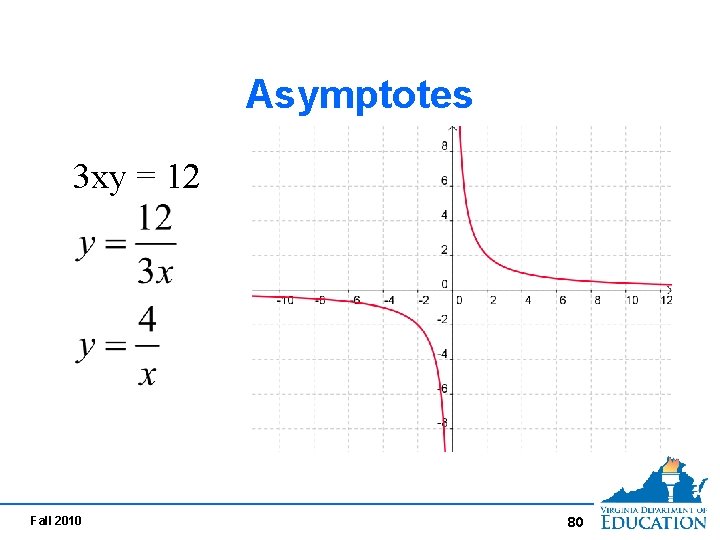
Asymptotes 3 xy = 12 Fall 2010 80

What do you know about this rational function? Fall 2010 81

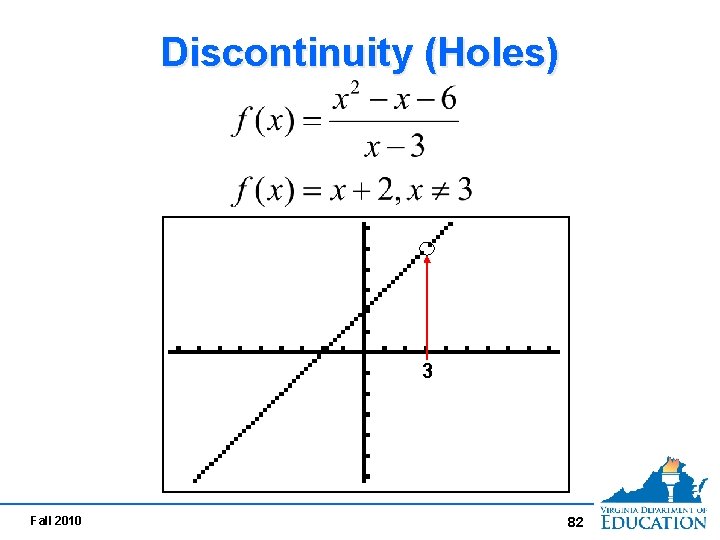
Discontinuity (Holes) 3 Fall 2010 82

Function Development 9 -12 Algebra I AFDA Algebra 2 Relation or function? Continuity Domain/range (includes Domain/range Zeros x- and y-intercepts Function values for elements of the domain Connections among representations Local/absolute max/min Intervals of inc/dec End behaviors Asymptotes 83 Fall 2010 discontinuous domains/ranges) Zeros x- and y-intercepts Function values for elements of the domain Connections among representations Local/absolute max/min Intervals of incr/decr End behaviors Asymptotes Inverse functions Composition of functions 83

Draw a function that has the following characteristics ? e l b i s ? s t o o p N t i y s h I W / y Wh Domain: {all real numbers} Range: {f(x)| f(x)>0} Increasing: {x| -2<x<2 U x>5} Decreasing: {x| 2<x<5} Relative maximum(turning point): (2, 4) Relative minimum(turning point): (-2, 1) End Behavior: As x approaches ∞, f(x) approaches ∞. As x approaches - ∞, f(x) approaches ∞. Asymptotes: y=0 Fall 2010 84

Revisit Placemat Consensus Functions Individual ideas are written here Common ideas are written here Individual ideas are written here Fall 2010 85