VARs and factors Lecture to Bristol MSc Time

VARs and factors Lecture to Bristol MSc Time Series, Spring 2014 Tony Yates

What we will cover Why factor models are useful in VARs Static and dynamic factor models ‘VAR in the factors’ Factor augmented VAR. Estimation of factors by principal components. Identification in Var in the factors or FAVAR: sign restrictions. • Application : Stock and Watson’s ‘Disentangling. . . ’ paper • • •

Some useful references • Stock and Watson: the implications of dynamic factor models for VAR analysis • Stock and Watson: Dynamic Factor Models • Stock and Watson 'Disentangling the causes of the 2007 -2009 recession‘ • Bai and Ng survey • Wikipedia entry on principal component analysis! • Geweke lecture

Dimensionality motivation for factor models • Omitting variables from our VAR means our reduced form shocks don’t span the structural shocks. – Eg Leeper Sims Zha (1996), 13, 18 variable VAR • But including more variables mean no of coeffs to be estimated expands by n^2*lags, while number of data points increases by n*T. • Central bank tracks 100 s of variables. Unless they are wasting time, maybe they should all enter? • Exercise: when does the curse of dimensionality bite?

Some interesting research with factor models • Quah and Sargent (1992): – you can capture many time series with just 2 factors – Confirmed by other authors later – Echoing early RBC claims, but using much more agnostic framework. – contradicting Smets-Wouters (2007) and similar with many shocks. – See also Sims and Sargent (1977)

More interesting factor model research • Stock and Watson: ‘Disentangling the causes of the crisis’[sic] – There are 8 factors, not 2 or 3! – Financial crisis was not a new shock, just larger versions of the old [‘Disentangling. . . ’] – Contradicts narrative of the crisis, and other DSGE based work. – We will return to this paper in more detail later.

Yet more interesting factor model research • Stock+Watson ‘Implications of dynamic factor models for VAR analysis’ – Redoes SVAR identification with factors. – Finds? An exercise for you to summarise it. • Harrison, Kapetanios, Yates: Estimating TVPDFM models using kernel methods. • Rudebusch: survey of macro-finance work on yield curve, including factor modelling.

A simple static factor model Y is our vector of observeables, driven by the latent factors F. Factors follow a VAR process as before.

Simple dynamic factor model It’s ‘dynamic’ because lags of the factors drive the observeables too.

Dynamic factor model written as a static factor model Sometimes convenient to create the enlarged state vector with current and lagged factors. And then re-write in terms of current values only of this enlarged state vector.

3 factor, 6 variable example. Here we have six variables, including 2 proxies for each of the variables in the simple sticky price model, which we will assume are the factors.

Restrictions in the measurement equation of the factor model Since we have a clear prior about which observables relate to which economic concept, we might restrict elements of the factor loading matrix lamda. If we didn’t, we would get less well determined estimates. Cost is that we have to be confident our restrictions are valid.
![Factor Augmented VAR [FAVAR] Imagine [quite realistically] that we thought inflation and interest rates Factor Augmented VAR [FAVAR] Imagine [quite realistically] that we thought inflation and interest rates](http://slidetodoc.com/presentation_image_h/3118698da6c60557403e1ad309e87be6/image-13.jpg)
Factor Augmented VAR [FAVAR] Imagine [quite realistically] that we thought inflation and interest rates were pretty well measured, but the output gap was not, and we had several alternative proxies for this. We would extract one factor from these output gap measures, then include it in a vector of ‘observables’ and estimate a VAR as before.

‘Blessing of dimensionality’ Obs on Y driven by a single factor F Now average over both sides of the equation Invoke assumption that errors uncorrelated with each other, and we get to the result that as n gets large, the average of our observeables uncovers the factor.

Estimation • Formulation as state-space model suggests estimation using Kalman Filter [putting it in a wide class of estimation problems, eg estimation of a DSGE/RBC model. • KF computes the likelihood for a given parameter value. • Then maximise wrt the parameters. • Problem: many parameters therefore large dimensional optimisation problem. • Can be reduced with priors about loading matrices.

Estimation: preliminaries. See Bai and Ng survey. Step by step, we stack the entire data set and factor decomposition in matrix form.

Variance-decomposition under the factor model Variance-covariance matrix of the data Contribution of the factors Variance-covariance of the idiosyncratic shocks Terms in the factors disappear, as we are going to use this normalisation to resolve identification.

Identification problem in the factor model We are trying to estimate F and lamda on the RHS here. But we can see that we can ‘rotate’ the factors and loadings with any invertible r*r matrix A, and still preserve the equation with the LHS data matrix.

Identification to resolve the indeterminacy of the factors and the loadings.

Estimation by Principal Components This is what we seek in estimation. Note that in finding k factors, we might not search for the true r factors. Like all estimation, finding the factors and loadings is an optimisation problem. By choice of the factors we try to minimise the residual sum of squares!

Recasting the minimisation problem and its solution. Two ways to proceed. Usually the same. Here we ‘concentrate out’ lamda from the objective function. We maximise the explained sum of squares. The estimated factors are the k eigenvectors of XX’, corresponding to the k largest eigenvalues.

Principal components estimation of the factors Define sample var cov matrix of observed data Least squares problem Solution. Lambdahats are scaled eigenvectors associated with r largest eigenvalues of sigmahat.
![Principal Components estimation [Bai and Ng, JOE in press] Write our factor model in Principal Components estimation [Bai and Ng, JOE in press] Write our factor model in](http://slidetodoc.com/presentation_image_h/3118698da6c60557403e1ad309e87be6/image-23.jpg)
Principal Components estimation [Bai and Ng, JOE in press] Write our factor model in matrix form. Factor etimation, of the factors and loadings, minimises this objective. Equivalent to the contribution of the idiosyncratic errors. These are constraints placed on the estimation.

PC estimates of factors and loadings Factors are the r scaled eigenvectors of the vcov matrix of the data. The loadings are products of the data matrix and the estimated factors. Watch out: papers sometimes use different notation, partly because the procedure only identifies separately the product of the factors and the loadings, and not each element.

Estimation of the full system • 2 -step procedure. • Having estimated the factors by principal components analysis… • …Treat the factors like you would observed data and then estimate the VAR in the factors using your chosen favoured method (MLE, OLS. . . ).

Identifying factors using sign restrictions Assume static factor model, and VAR(1) in the factors. Just as with VARs in the variables, we can factor the vcov matrix of shocks to factors, and factor further using an orthonormal matrix C. We draw multiple C’s, and then inspect the sign of the impact on observeables in the same way as before, except now we have to substitute into the measurement equation and premultiply by lamda.

Description in words of sign restriction factor identification • Example: monetary policy shock. – Normal VAR. A mp shock is one that if it drives cb rate up, will drive output down, inflation down. – DFM. A mp shock is a shock to the VAR in the factors such that, given the factor loadings estimated in stage 1, if it drives the cb rate up, it also drives the inflation rate down and output down. – One point of factor model would be to have many proxies for inflation. So restriction here would be that it would drive all (eg) proxies for inflation down. Or perhaps most of them.
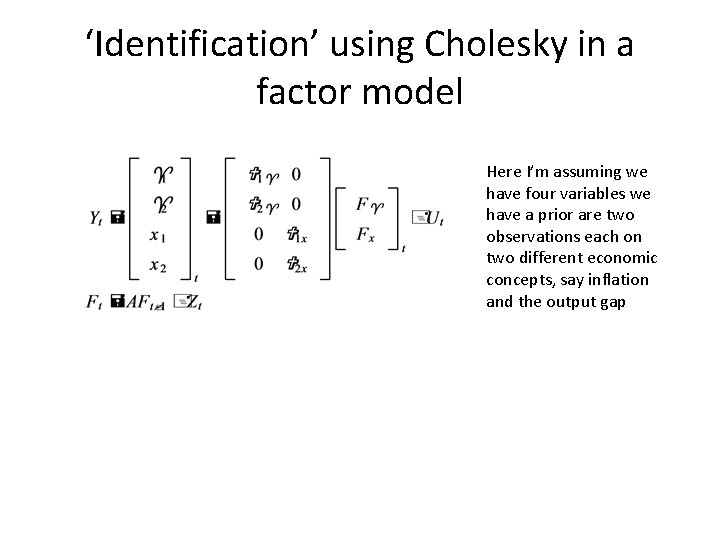
‘Identification’ using Cholesky in a factor model Here I’m assuming we have four variables we have a prior are two observations each on two different economic concepts, say inflation and the output gap

Cholesky i. d. with factors As before, we seek the elusive B 0 inv, which now encodes contemp relationship between the factors If we are ok with a lower-triangular B 0 inv connecting the factors then we simply take it to be the cholesky factor of the vcov matrix of residuals in the var in the factors. Impuse response of factors computed as before. But impulse response of observables requires substituting into the measurement equation.

Application: Stock and Watson’s ‘Disentangling. . ’ paper Trying to explain the recession. Note all real series show big drop relative to trend. Not surprising therefore that ‘common component’ [lamdahat*F] explains a lot. Their research question is: Was it bigger versions of old shocks that explain the crisis. . Or new shocks.
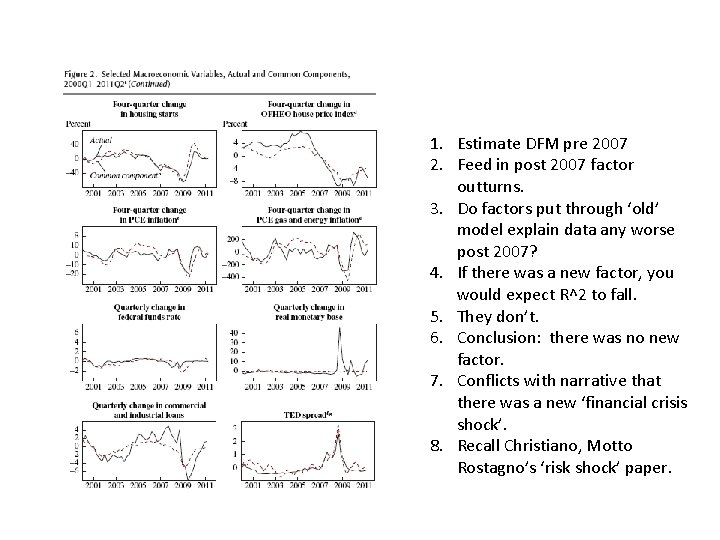
1. Estimate DFM pre 2007 2. Feed in post 2007 factor outturns. 3. Do factors put through ‘old’ model explain data any worse post 2007? 4. If there was a new factor, you would expect R^2 to fall. 5. They don’t. 6. Conclusion: there was no new factor. 7. Conflicts with narrative that there was a new ‘financial crisis shock’. 8. Recall Christiano, Motto Rostagno’s ‘risk shock’ paper.

SW’s R^2 exercise Factors and factor loadings estimated over pre-2007 sample R^2 here can’t be >1, but it can be <1 (and sometimes is as we will see) If factors do a good job at explaining the series, then should be close to 1.
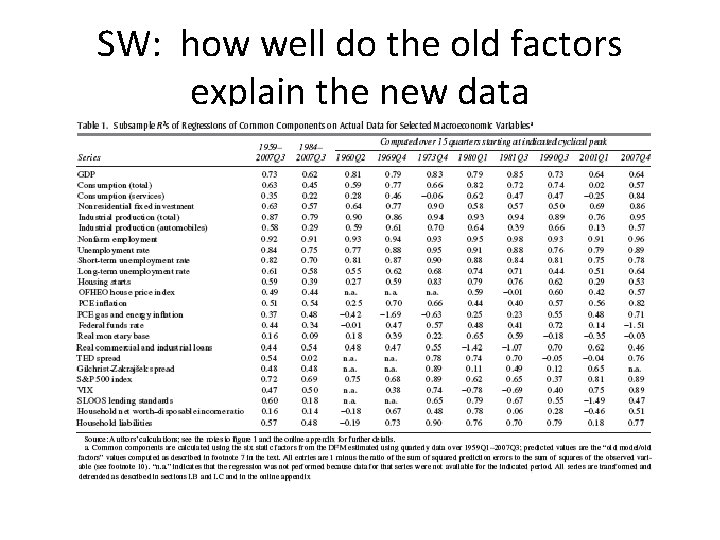
SW: how well do the old factors explain the new data

SW: Tests for break in factor loadings Majority of tests accept stability. Tendency to reject caused by change in 1984. That relates to earlier work dating this as the start of the ‘Great Moderation’. Implication is that 2007 not responsible for many breaks.

SW: indication of existence of new factor Construct vcov of idiosyncratic shocks, using pre-crisis loadings and factors. Compute ratio of first to sum of remaining eigenvalues. Large value of this implies more correlation between idiosyncratic shocks. Tests for equality of this ratio before and after crisis. P value of 0. 59.

SW: evidence of increased factor variance So if it wasn’t new factors, then it must be the old ones that increased. This is the sd of lamdahat*F for selected series. You can see it increases during the crisis.

Post-script: Stock-Watson and the old two factor finding • They say you need 7 or 8 factors, not 2. • The old finding was, they said, based on i) too narrow a set of data, and ii) the early sample period. • This is a huge deal in the business cycle literature, but the finding doesn’t seem to have attracted all that much attention.

Recap • Factor models are a way to overcome curse of dimensionality. In fact there is a ‘blessing of dimensionality. ’ • Can be combined with VARs: FAVAR, VAR in the factors. Estimated using PCA. • Factors and loadings chosen to minimise contribution of idiosyncratic error variance. • Stock and Watson’s financial crisis application.
- Slides: 38