Variations of Weighted Fair Queueing Issues with WFQ

Issues with WFQ 1. WFQ does not run behind GPS by more than Lmax/C.

Weighted Round Robin (WRR) • Parameters: – Li is the average packet size of

Weighted Round Robin (WRR) • If all flows are active and packets are equal

Deficit Round Robin (DRR) • Can be viewed as – Improvement to WRR without

Deficit Round Robin (DRR) • If queue is empty: Qi=0 Here: Quantum is 75

Deficit Round Robin (DRR) • The share of flow i: • The bandwidth guarantee

Self-Clocked Fair Queueing (SCFQ) Start-time Fair Queueing (SFQ)

Self-Clocked Fair Queueing (SCFQ) • Objective: Avoid the need to keep track of system

WFQ and WF 2 Q • 12 flows, all packets have size 1, C

Worst-Case Fair Queueing • Issue: While WFQ never falls behind the fluid-flow schedule by

Slides: 18

Download presentation

Variations of Weighted Fair Queueing

Issues with WFQ 1. WFQ does not run behind GPS by more than Lmax/C. However, WFQ may run ahead of GPS by a lot – Improvement: Bound the time by which WFQ can run ahead of GPS WF 2 Q, WF 2 Q+ 2. Implementation overhead of computing virtual time – Improvement: Avoid virtual time computation, while maintaining fairness properties SCFQ, SFQ, WF 2 Q+ 3. Need to maintain a sorted queue (sorted in order of timestamps) – Improvement: Use a round-robin approach WRR, DRR (Stratified Round Robin)2

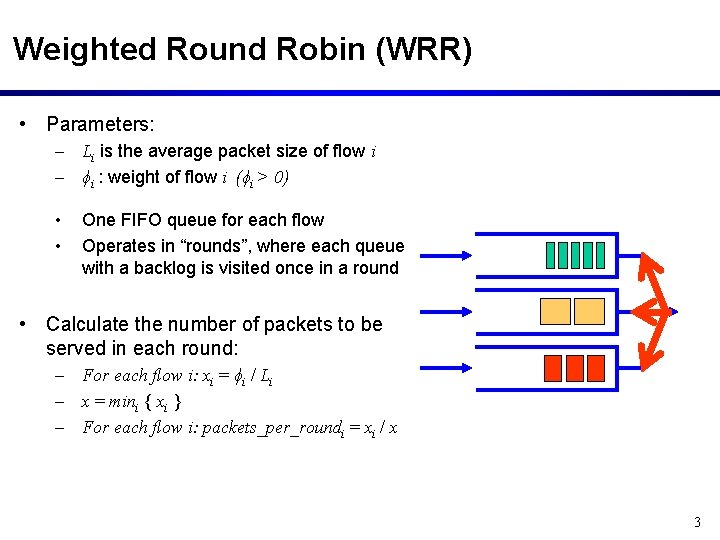
Weighted Round Robin (WRR) • Parameters: – Li is the average packet size of flow i – ϕi : weight of flow i (ϕi > 0) • • One FIFO queue for each flow Operates in “rounds”, where each queue with a backlog is visited once in a round • Calculate the number of packets to be served in each round: – For each flow i: xi = ϕi / Li – x = mini { xi } – For each flow i: packets_per_roundi = xi / x 3

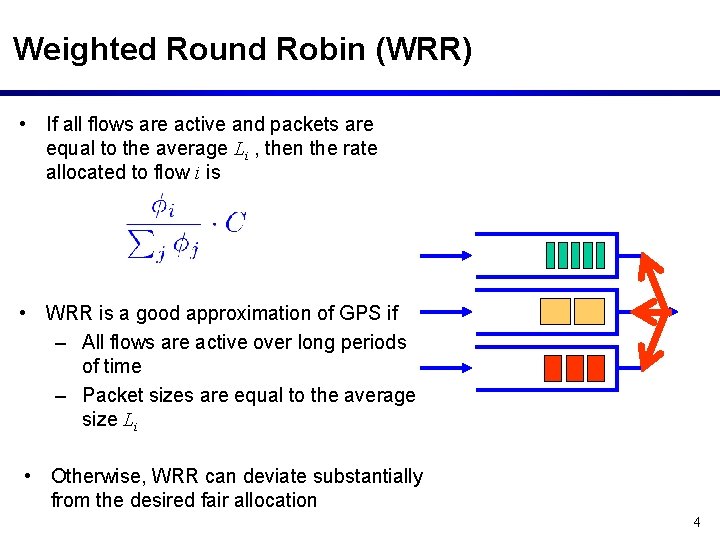
Weighted Round Robin (WRR) • If all flows are active and packets are equal to the average Li , then the rate allocated to flow i is • WRR is a good approximation of GPS if – All flows are active over long periods of time – Packet sizes are equal to the average size Li • Otherwise, WRR can deviate substantially from the desired fair allocation 4

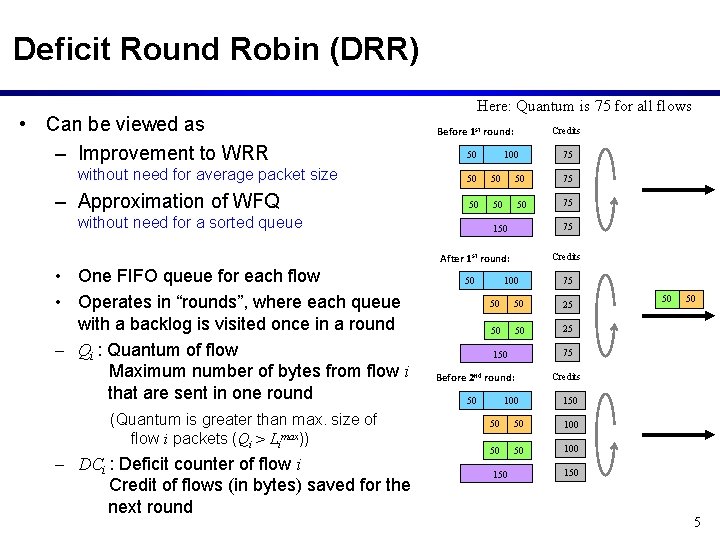
Deficit Round Robin (DRR) • Can be viewed as – Improvement to WRR without need for average packet size – Approximation of WFQ Here: Quantum is 75 for all flows Before 1 st round: 50 Credits 100 50 50 50 75 without need for a sorted queue 75 150 After 1 st round: • One FIFO queue for each flow • Operates in “rounds”, where each queue with a backlog is visited once in a round – Qi : Quantum of flow Maximum number of bytes from flow i that are sent in one round (Quantum is greater than max. size of flow i packets (Qi > Limax)) – DCi : Deficit counter of flow i Credit of flows (in bytes) saved for the next round 75 50 Credits 100 75 50 50 25 Before 2 nd round: 100 Credits 150 50 50 100 150 50 75 150 50 50 150 5

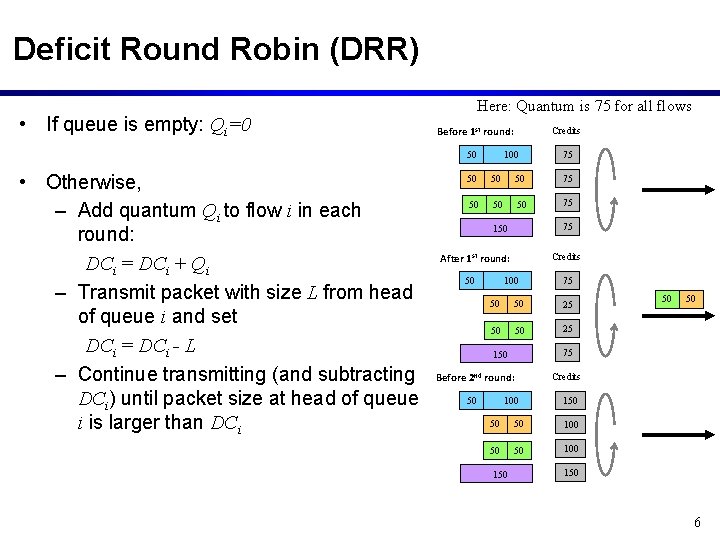
Deficit Round Robin (DRR) • If queue is empty: Qi=0 Here: Quantum is 75 for all flows Before 1 st round: 50 • Otherwise, – Add quantum Qi to flow i in each round: DCi = DCi + Qi – Transmit packet with size L from head of queue i and set DCi = DCi - L – Continue transmitting (and subtracting DCi) until packet size at head of queue i is larger than DCi Credits 100 75 50 50 50 75 75 150 After 1 st round: 50 Credits 100 75 50 50 25 Before 2 nd round: 100 Credits 150 50 50 100 150 50 75 150 50 50 150 6

Deficit Round Robin (DRR) • The share of flow i: • The bandwidth guarantee of flow i: • Fairness metric for two backlogged flows i and j in [t 1, t 2]: 7

Self-Clocked Fair Queueing (SCFQ) Start-time Fair Queueing (SFQ)

Self-Clocked Fair Queueing (SCFQ) • Objective: Avoid the need to keep track of system virtual time • Idea: – System virtual time keeps track of the service received by a flow with weight ϕi =1 – Virtual finishing time of a packet is the finishing time of the packet in system virtual time è Virtual finishing time encodes information on system virtual time è Use virtual finishing time of a packet instead of system virtual time 9

Worst-Case Fair Queueing (WF 2 Q)

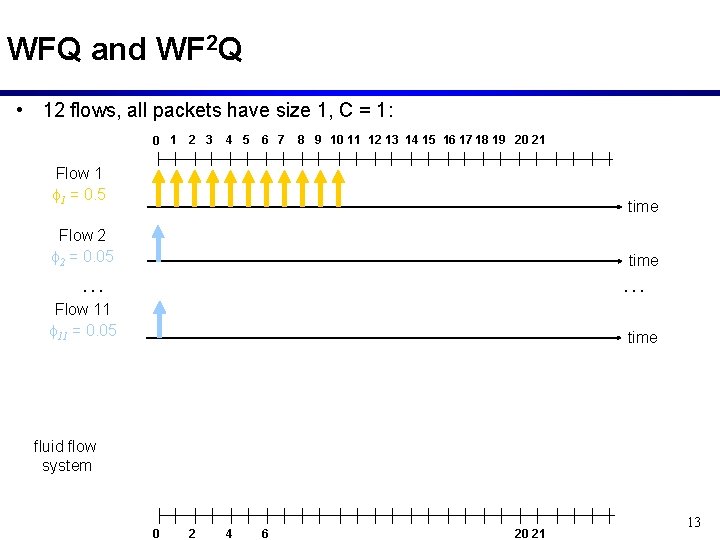
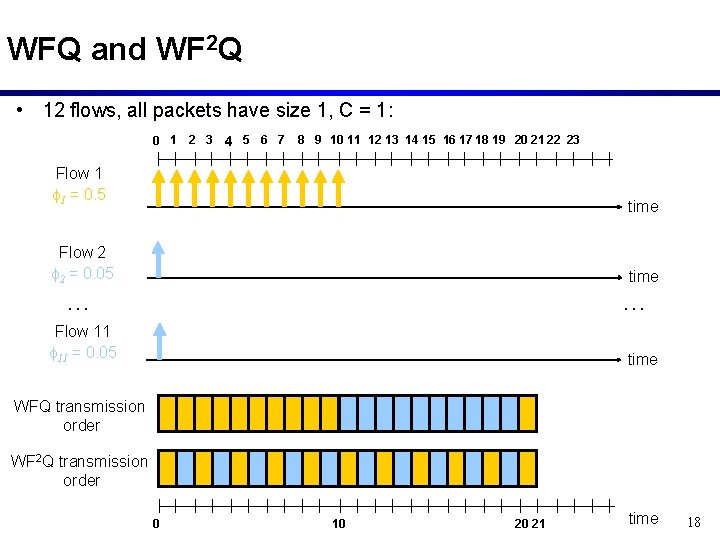
WFQ and WF 2 Q • 12 flows, all packets have size 1, C = 1: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 Flow 1 f 1 = 0. 5 time Flow 2 f 2 = 0. 05 time … … Flow 11 f 11 = 0. 05 time fluid flow system 0 2 4 6 20 21 13

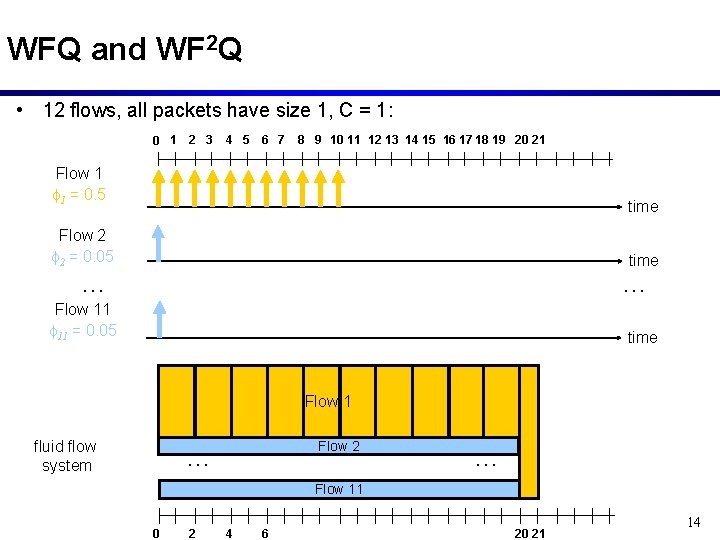
WFQ and WF 2 Q • 12 flows, all packets have size 1, C = 1: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 Flow 1 f 1 = 0. 5 time Flow 2 f 2 = 0. 05 time … … Flow 11 f 11 = 0. 05 time Flow 1 fluid flow system Flow 2 … … Flow 11 0 2 4 6 20 21 14

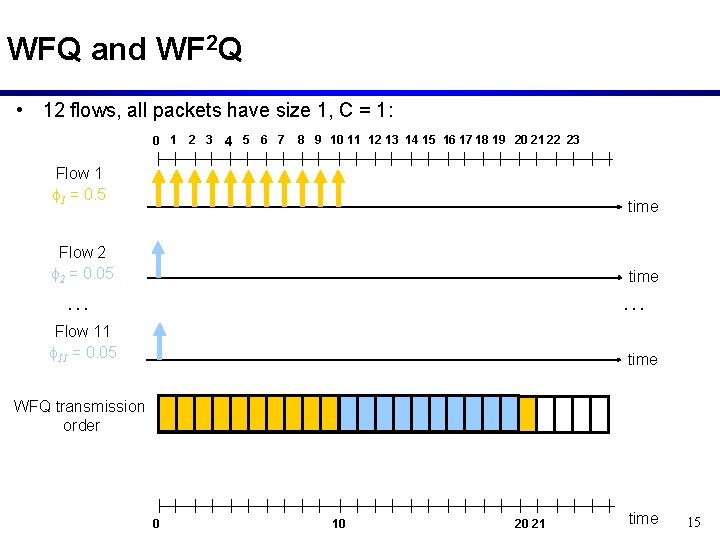
WFQ and WF 2 Q • 12 flows, all packets have size 1, C = 1: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Flow 1 f 1 = 0. 5 time Flow 2 f 2 = 0. 05 time … … Flow 11 f 11 = 0. 05 time WFQ transmission order 0 10 20 21 time 15

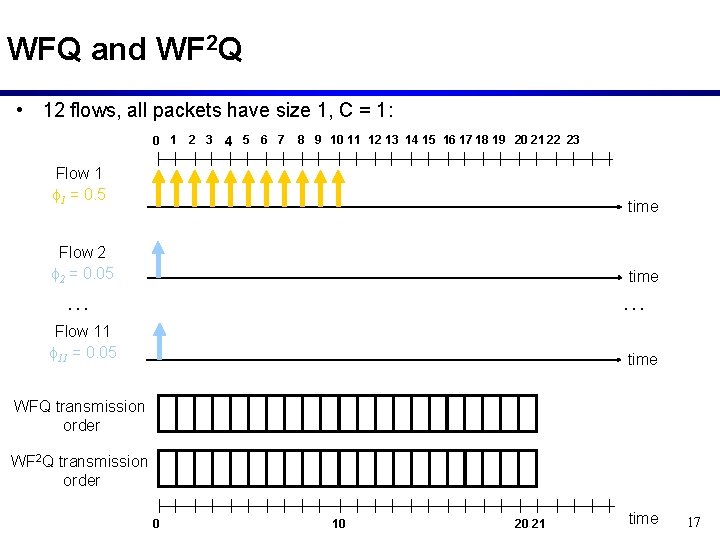
Worst-Case Fair Queueing • Issue: While WFQ never falls behind the fluid-flow schedule by more than one packet size, it can run ahead of the fluid-flow schedule by an arbitrary amount. • WF 2 Q Scheduling: – Only considers packets for transmission that have already started transmission in the fluid-flow system – Of these, it selects the packet with the smallest finishing time (in the fluid-flow system) • WF 2 Q Properties: – Like WFQ, WF 2 Q never falls behind the fluid-flow schedule by more than one packet size ( same end-to-end delay bounds as WFQ) – Unlike WFQ, it never runs ahead of the fluid-flow schedule by more than one packet size 16