Variations in the teaching of functions Luxizi ZHANG

Variations in the teaching of functions Luxizi ZHANG Ph. D student luxizi. zhang@ens-lyon. fr supervisors Jiansheng BAO East China Normal University, China Luc TROUCHE École Normale Supérieure de Lyon, Ife, France December, 11 th 2018, ENS de Lyon, France

Outlines • Motivation and background • Research questions • Theoretical considerations • Methodology • My observation in French teachers' class • Discussions

Motivation and Background The reason why I choose this topic? ·Teaching and learning mathematics through variation has a long history in China and has been used consciously or unconsciously by teachers (Bao et al. , 2003). • Function is an important mathematics topic in high school both in China and in France: - This theme combines a variety of representations (graphs, tables of values, algebraic formulas) - Possible links with the “real world” (Gueudet et al. , 2016) - Offering many opportunities for teachers teaching through variation

Motivation and Background My Expectations: We wonder if there is also variation in french mathematics teaching? What kind of variation? What are the similarities and differences of variation through teaching between these two countries? Through the comparison, I want to construct a model of teaching through variation. In the end, I want to use this model to help teachers' professional development

Research questions: 1. Is it possible to analyze the French mathematics teaching cases by using Chinese theory of variation (“Bianshi” theory)? 2. How does French mathematics teaching reflect variation?

Theoretical considerations (in China) Gu's BS theory (Bianshi, 变式): It is intended to capture and make explicit good practices in mathematics teaching in China; it was named and codified by Gu Ling-yuan (Pang et al. , 2017). Gu (1981) proposed Conceptual Variation and Procedural Variation, and then later discussed the concept and effects of core connection and instructional “Pudian” (Gu et al. , 2017).

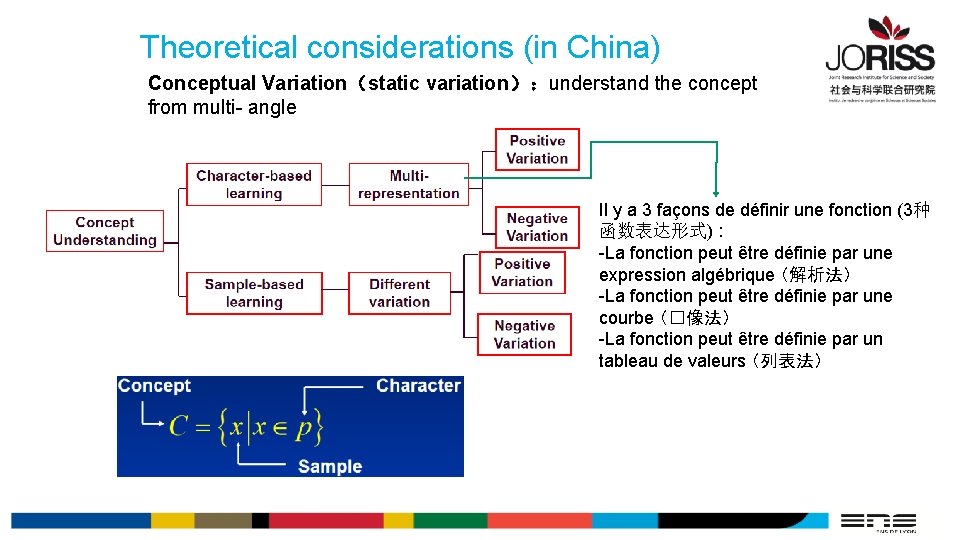
Theoretical considerations (in China) Conceptual Variation（static variation）：understand the concept from multi- angle Il y a 3 façons de définir une fonction (3种 函数表达形式) : -La fonction peut être définie par une expression algébrique （解析法） -La fonction peut être définie par une courbe （�像法） -La fonction peut être définie par un tableau de valeurs （列表法）

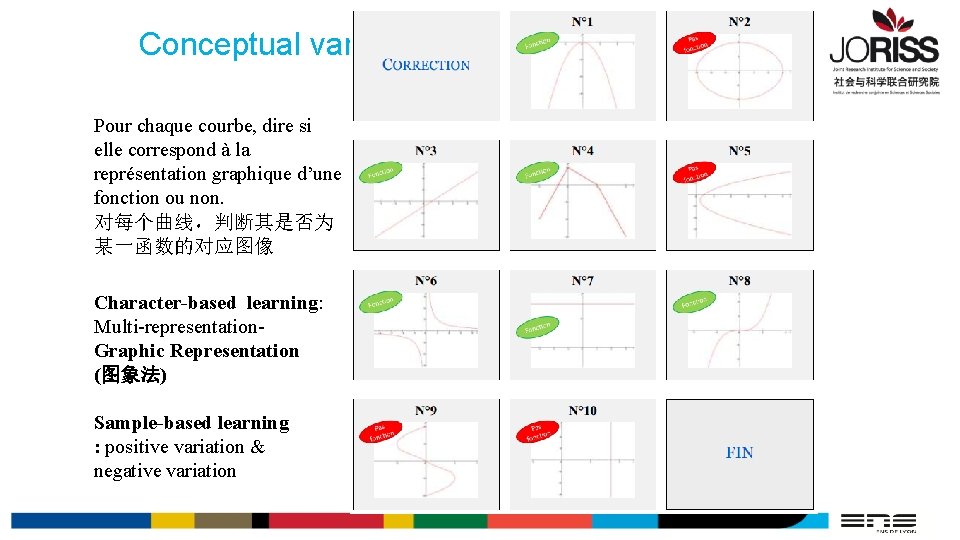
Conceptual variation in class Pour chaque courbe, dire si elle correspond à la représentation graphique d’une fonction ou non. 对每个曲线，判断其是否为 某一函数的对应图像 Character-based learning: Multi-representation. Graphic Representation (图象法) Sample-based learning : positive variation & negative variation

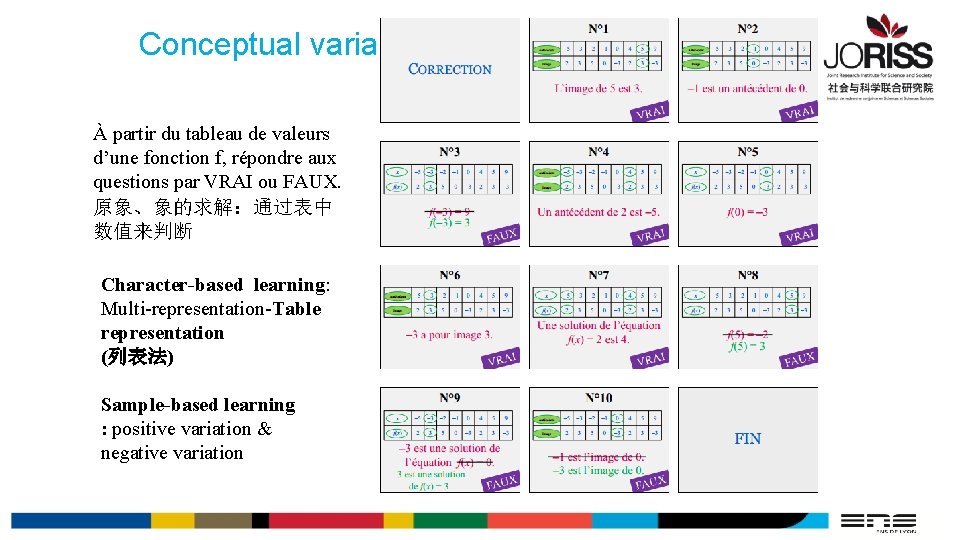
Conceptual variation in class À partir du tableau de valeurs d’une fonction f, répondre aux questions par VRAI ou FAUX. 原象、象的求解：通过表中 数值来判断 Character-based learning: Multi-representation-Table representation (列表法) Sample-based learning : positive variation & negative variation

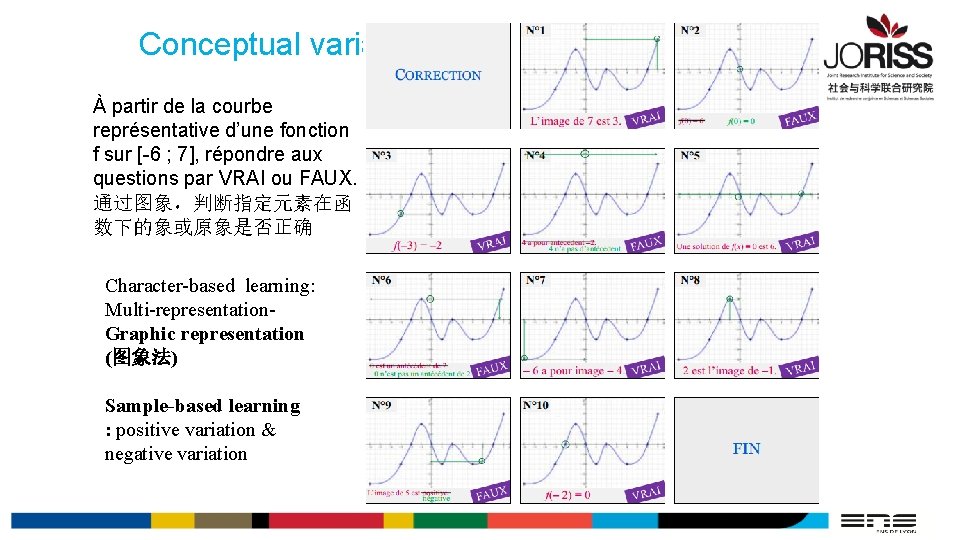
Conceptual variation in class À partir de la courbe représentative d’une fonction f sur [-6 ; 7], répondre aux questions par VRAI ou FAUX. 通过图象，判断指定元素在函 数下的象或原象是否正确 Character-based learning: Multi-representation. Graphic representation (图象法) Sample-based learning : positive variation & negative variation

Conceptual variation in class À partir de la forme explicite d’une fonction f, répondre aux questions par VRAI ou FAUX. 通过图象，判断指定元素 在函数下的象或原象是否 正确 Character-based learning: Multi-representation. Algebraic representation(解 析法) Sample-based learning : positive variation & negative variation

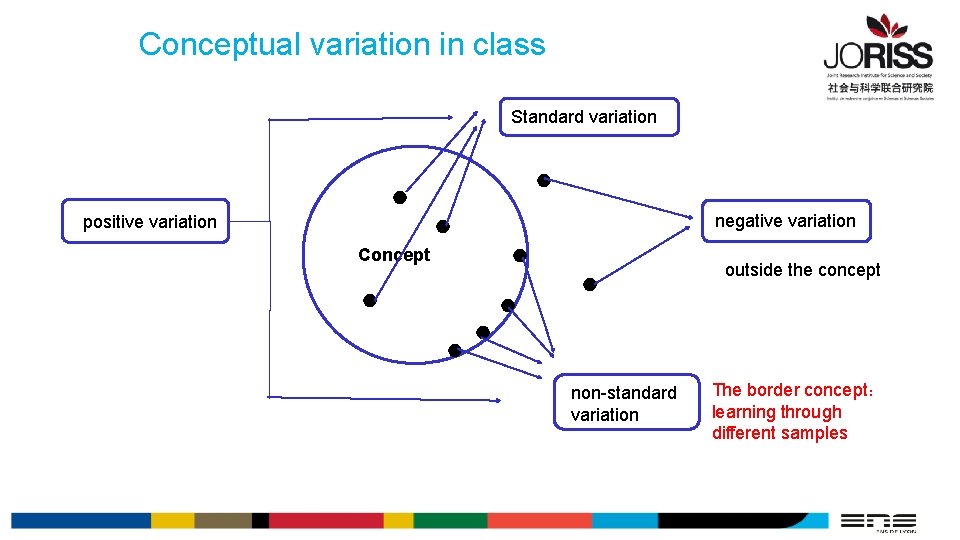
Conceptual variation in class Standard variation ● ● positive variation negative variation ● Concept ● ● ● outside the concept ● ● ● non-standard variation The border concept： learning through different samples

Theoretical considerations (in China) Procedural Variation

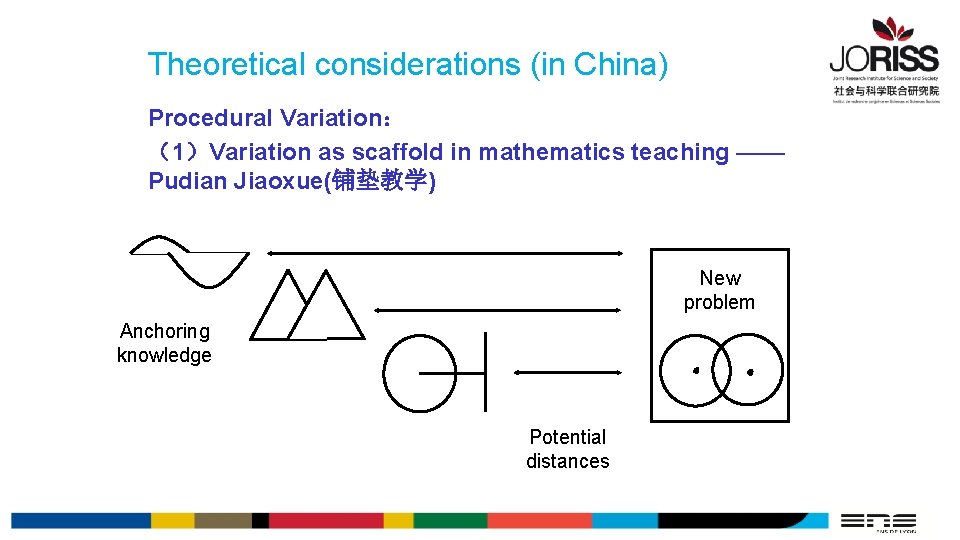
Theoretical considerations (in China) Procedural Variation： （1）Variation as scaffold in mathematics teaching —— Pudian Jiaoxue(铺垫教学) New problem Anchoring knowledge Potential distances

Theoretical considerations (in China) Step 1 Students calculate specific numbers Partie A : Premiers calculs 1) Calculer la recette obtenue si le producteur récolte et vend ses patates le 31 mai. 2) Si le producteur récolte et vend ses pommes de terre le 1 er juin, donner : a) La quantité récoltée : b) Le prix au kilogramme de pommes de terre : c) La recette obtenue par la vente de cette récolte : 3) Calculer la recette obtenue si le producteur récolte et vend le 2 juin : A部分：第一次计算 1）计算 5月31日生产者收获并出售土豆时获得的收入。 2）如果生产者在 6月1日收获并出售他的土豆，请写出： （a）收获量： （b）每千克土豆的价格： （c）出售土豆所得收入： 3）计算生产者在 6月2日收获并卖出土豆所能得到的收入：

Theoretical considerations (in China) Step 2 Students gives the algebraic expressions of the function B部分：函数值的列表 1)第x天的函数表示为： a) 收获土豆的数量：q(x)= b) 每千克的价格：p(x)= 2) 第x天收获并出售土豆所得收入的函数表示为： 3) 证明r(x)也可以写作

Theoretical considerations (in China) Step 3 Students working with calculator for value table and graph of function table representations 4) 我们想在列表中显示这些函数的数值 (限制在 6月内, 从第一天到第 30天) 使用计算器来完成表格。 5) Représenter la fonction dans le repère orthogonal donné ci-dessous Pour cela visualisez d’abord la courbe à tracer sur la calculatrice. 6) En étudiant le tableau de valeurs et la courbe, déterminer le jour de juin que doit choisir le producteur pour obtenir la recette maximale, ainsi que la valeur de cette recette. graphic representations 5）在下图给出的正交坐标系中表示函数。为此，首先要先在计算器上绘制出函数曲线。 6）通过研究函数值列表和函数曲线，确定生产者在 6月可以获得最大收入的日期，以及最大收入 的数值。

Theoretical considerations (in China) Characteristics of Pudian Jiaoxue(铺垫教学) • • Step by step Confidence Goal-driven One way, different speeds

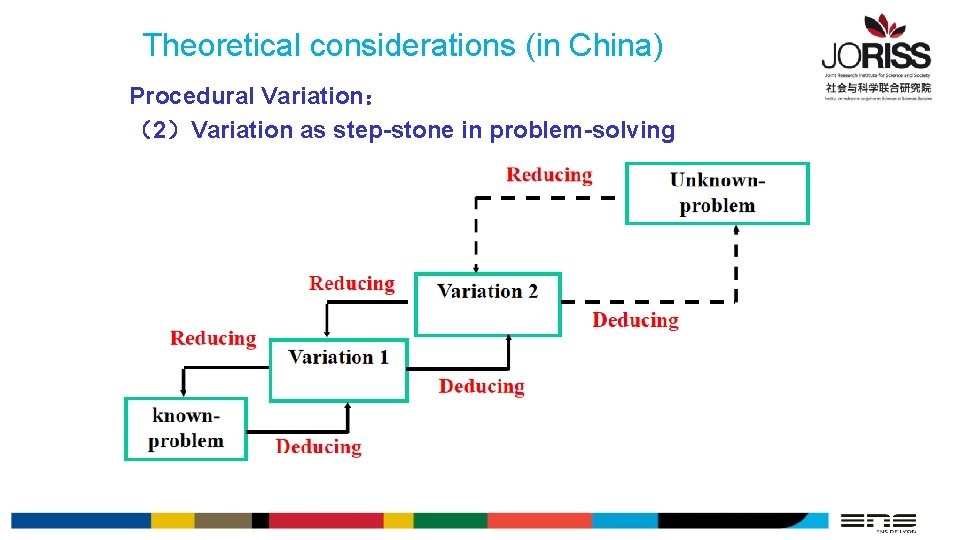
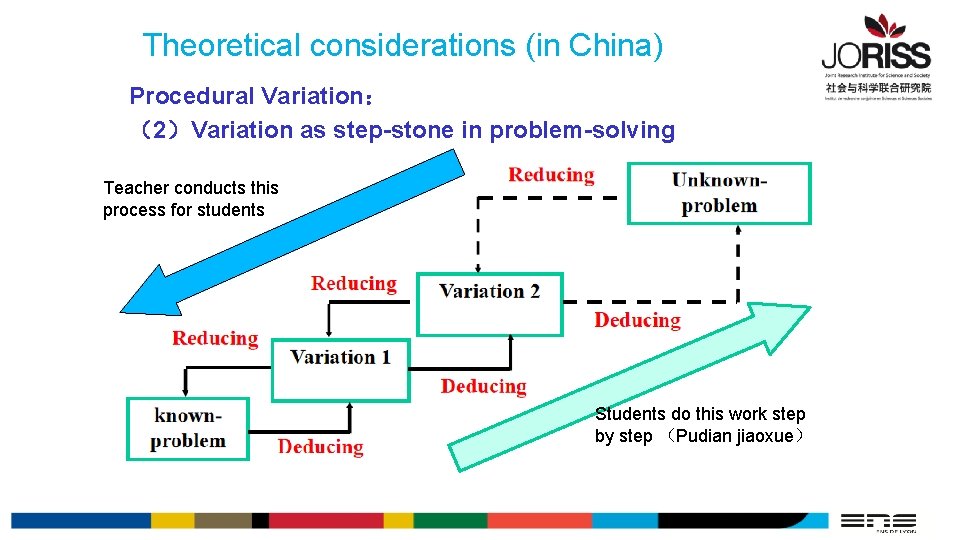
Theoretical considerations (in China) Procedural Variation： （2）Variation as step-stone in problem-solving

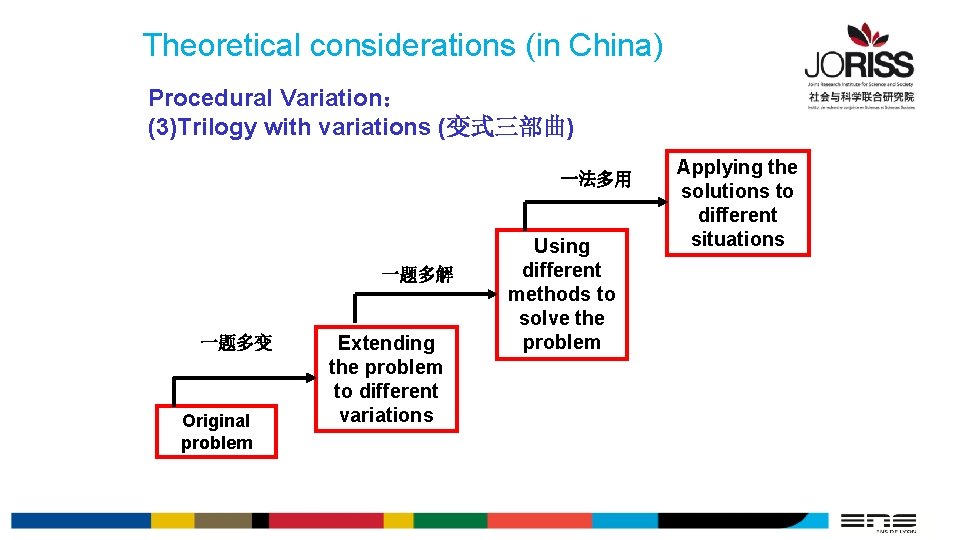
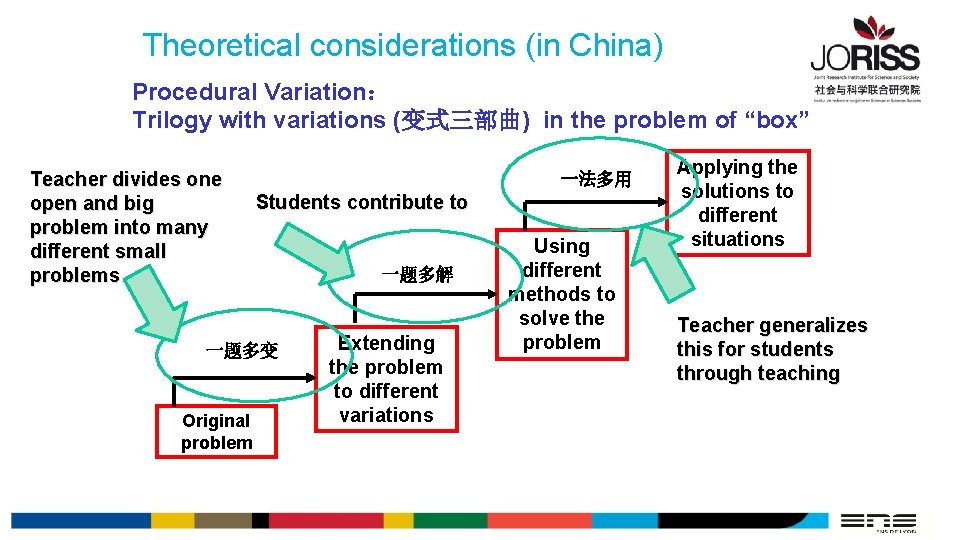
Theoretical considerations (in China) Procedural Variation： (3)Trilogy with variations (变式三部曲) 一法多用 一题多解 一题多变 Original problem Extending the problem to different variations Using different methods to solve the problem Applying the solutions to different situations

Theoretical considerations (in China) Sample Lesson： La boîte sans couvercle Le problème posé : À partir d’une feuille de papier au format A 4, on veut construire le patron d’une boite sans couvercle qui a la forme d’un parallélépipède rectangle et qui a le plus grand volume possible. Quelles sont ses dimensions ? 提出问题： 从一张A 4纸中，我们想要制作一个没有盖子 的盒子，其形状为长方体，并且具有最大可能 的体积。它的尺寸是多少？

Theoretical considerations (in China) Step 1: Group work (3 -4 students in each group) We can get Students' solutions from their oral presentation and their written synthesis 1) Wrong

Theoretical considerations (in China) 2) using technology 3) use value table and draw graph to find the maximum

Theoretical considerations (in China) Procedural Variation： Trilogy with variations (变式三部曲) in the problem of “box” Teacher divides one open and big problem into many different small problems 一法多用 Students contribute to 一题多变 Original problem 一题多解 Extending the problem to different variations Using different methods to solve the problem Applying the solutions to different situations Teacher generalizes this for students through teaching

Theoretical considerations (in China) Procedural Variation： （2）Variation as step-stone in problem-solving Teacher conducts this process for students Students do this work step by step （Pudian jiaoxue）

Theoretical considerations (in France) Brousseau’s Theory of Didactical Situations （1986） Major work: theory of didactical situations The fundamental idea of ‘situations’ is defined by Warfield (2014), in a short book ‘inviting to didactics’: A Situation describes the relevant conditions in which a student uses and learns a piece of mathematical knowledge. At the basic level, these conditions deal with three components: a topic to be taught, a problem in the classical sense and a variety of characteristics of the material and didactical environment of the action’.

Theoretical considerations (in France) Brousseau’s Theory of Didactical Situations （1986） Three structuring notions of Brousseau’s theory: -a-didactical situations: occur in the classroom, and have the goal of reproducing the conditions of a real mathematical activity dealing with a determined concept: i. e. a mathematical situation. In the course of an a-didactical situation, the students are supposed to produce a correct and adequate action or mathematical text without receiving any supplementary information or influence. -didactical situations: the actions taken by a teacher to set-up and maintain an a-didactical situation designed to allow students to develop some goal concept(s).

Theoretical considerations (in France) Brousseau’s Theory of Didactical Situations （1986） - milieu: In particular, the teacher sets up the milieu, which includes the physical surroundings, the instructions, carefully chosen information, etc. The milieu may, or may not include a material element (for example Cabri geometry), and other cooperating or concurrent students, etc. but it does at the least include the savoirs 20 of the subject, and certain of her current connaissances. It is essential that the milieu is designed in a way that it only obeys “objective” necessities, and that the student be convinced of that fact. Once that design is in place, the teacher’s mandate is limited to making sure the students focus on the milieu and not on the teacher”

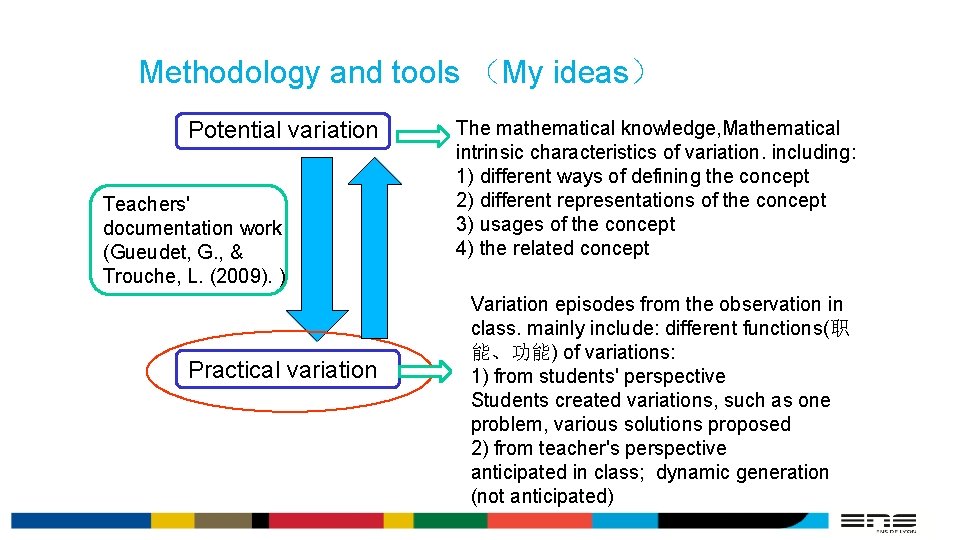
Methodology and tools （My ideas） Potential variation Teachers' documentation work (Gueudet, G. , & Trouche, L. (2009). ) Practical variation The mathematical knowledge, Mathematical intrinsic characteristics of variation. including: 1) different ways of defining the concept 2) different representations of the concept 3) usages of the concept 4) the related concept Variation episodes from the observation in class. mainly include: different functions(职 能、功能) of variations: 1) from students' perspective Students created variations, such as one problem, various solutions proposed 2) from teacher's perspective anticipated in class; dynamic generation (not anticipated)

References Bao, J. , Huang, R. , Yi, L. , & Gu, L. (2003). Continued study of “Bianshi Jiaoxue” [Teaching with variation]. Mathematics Teaching, 2, 6 -10. Brousseau, G. (1986). Fondements et méthodes de la didactique des mathématiques, Recherches en didactique des mathématiques, 7(2), Gu, F. , Huang, R. , & Gu, L. (2017). Teaching and Learning Mathematics through Variation. In Huang, R. , & Li, Y. (Eds. ). Teaching and Learning Mathematics through Variation. Confucian Heritage Meets Western Theories (pp. 13 -41). Rotterdam: Sense Publishers. Gu, L. , Huang, R. , & Marton, F. (2004). Teaching with variation: An effective way of mathematics teaching in China. In L. Fan, N. Y. Wong, J. Cai, & S. Li (Eds. ), How Chinese learn mathematics: Perspectives from insiders (pp. 309– 348). Singapore: World Scientific Gueudet, G. , & Trouche, L. (2009). Towards new documentation systems for mathematics teachers? Educational Studies in Mathematics, 71(3), 199 -218. Pang, M. , Bao, J. , & KI, W. (2017). 3. ‘BIANSHI’ and the variation theory of learning: Illustrating two frameworks of variation and invariance in the teaching of mathematics. In Huang, R. , & Li, Y. (Eds. ). Teaching and Learning Mathematics through Variation. Confucian Heritage Meets Western Theories (pp. 44 -67). Rotterdam: Sense Publishers.