Variables Values Atoms Lists Variables in Lisp differ

Variables, Values, Atoms, Lists • Variables in Lisp differ from other languages – They are not declared by type • their type is determined at run-time, and their type can change – They are dynamic • at run-time, storage space is made available for them from the heap, making them pointers – Computed values are stored in memory locations, and then pointed at • e. g. , (+ 3 5) creates a memory location storing 8 and returns a pointer to the memory location storing 8 • Variables do have to be declared but unlike Java or C/C++, variables are usually not declared with a type – The location of their declaration (and the type of statement used to declare them) dictates their scope

What is Scope? • The simplest definition for scope is “the instructions in which a given variable can be referenced” – The scope of the variable is the range of instructions where that variable is bound • a variable is a name and it is bound to a memory location that stores a pointer • inside its scope, referencing the variable actually references the memory location it is bound to • outside of its scope, there is no memory location and so a reference yields an error – Scope for CL variables • Global – known everywhere in the run-time environment and in any function if explicitly declared as special • Local – known only within the let statement it is defined (or other construct such as the loop variable(s) of a Do statement) • Parameter – known throughout the body of the function

The Let* Statements • The Let and Let* statements are used to declare a block of instructions in which variables can be declared locally – The scope of these variables is the let statement itself • (let* (variables go here) …) – the “)” after the statements ends the scope of these variables • the variables listed are all initialized to nil unless you initialize them yourself • such initializations are done by placing the variable and its initial value in ( ) as in (let* (a b (c 5)) … ) – a and b are nil, c is 5 • the initialization can be performed by calling functions as well leading to some complex looking code – (let* ((a 3) (b (square a)) (c (- (/ b 3) 1)) (d (round (/ c 12))))

Let* vs. Let • In general, the two statements are the same – But, like the previous example, if you want to initialize variables using values in the let statement, you must use let* – If you either are not initializing variables, or you are initializing the variables with values/function calls that do not utilize any variables in that list, you can use let • Both let* and let can be nested, so we can get around the restriction in let by nesting lets together (let* ((a 5) (b (+ a 1))) …) (let ((a 5)) (let ((b (+ a 1))) …)) But not (let ((a 5) (b (+ a 1))) …)

Scope Example • Local variables are (defun scopeexample (x) statically scoped (let ((y 1) (z 0)) – their scope can be …; any reference to x is the parameter determined by their …; any reference to y has the value 1 position within the code (let ((y z)) • Global variables are … ; reference to y with the value 0 dynamically scoped ) ; ends the scope of this version of y – their use is based on the …; reference to y has the value 1 most recent definition with respect to the functions ) ; y and z are no longer accessible being called ) ; ends the function and x’s scope • Because of the complexity of dealing with dynamic scoping, we will try to avoid using global variables as much as possible!

Shadowing Variables • Variables of the same name can shadow earlier declared variables – There is no real reason to use the same named variable, but if you do it, then only the most recently declared variable will be accessible (let ((x 1)) (print x) (let ((x 2)) (print x)) (let ((x 3)) (print x)) 1 2 3 1 (defun foo (x) (let ((y x)) (let ((x 2)) (setf y (* 2 x))) (setf x (* 2 y)) x)) This function should return the param * 4 but (foo 3) returns 8 instead of 12, why?

Self-Evaluating Forms • In CL, everything entered into the interpreter is evaluated – For functions, apply the function to the parameters, where the parameters are evaluated before the function is applied • (foo a b c) – a, b and c are evaluated, those values are passed to foo • (foo (bar a) (bar b) (bar c)) – this is the same, but recursive, so evaluating (bar a) means evaluating a and applying bar to it, etc • Items that evaluate to themselves are – – – Numbers Characters Strings T and nil Variables evaluate to the value in memory being pointed to • so (setf a 5) means that a evaluates to 5 • To prevent an item from evaluating – use (quote item) or just ’item

Defvar, Defparameter, Defconstant • Defvar, Defparameter used to declare global variables – (defvar var) to declare only – (defvar value), (defparameter value) to declare and initialize • You can’t declare a defparameter without giving it an initial value • Use defparameter if the variable already has an assigned value (defvar can not be used in such a case) – Note: these two functions return the variable, not its value so you get: CL-USER 68 : 1 > (defparameter *x* 1) *X* • Defconstant declares a constant – (defconstant var value) • note: you should declare global variables outside of a function for clarity, but it is permissible to assign them within a function, in which case the variable will continue to exist after the function terminates

Special • Whether global variables are declared inside or outside a function, they need to be denoted as globals when used inside any given function – This is done by declaring them as special • (declare (special *name*)) – If you don’t do this, the CL interpreter will probably guess that the undeclared variable is special and tell you this by means of a warning • but explicitly declaring it as such ensures that you won’t have any problem – The naming convention is to place the name in ** • it is generally bad programming practice to use global variables, but the option is there for you and there are certain occasions in functional programming where it becomes very useful

Assignment Operations • The general-purpose assignment function is setf – This is actually a special form which has a side effect • (setf var value) roughly the same as var = value in Java • but, if value is not already in memory, it is deposited into heap memory and the pointer var is changed to point at this new memory – the change of pointer location is the side effect, so interestingly this is a function whose main purpose is the side effect • the function also returns the value so this can be used in other function calls – (setf a (+ (setf b 5) 1)) b is set to 5, a is set to 6 – (or (setf a (and b c)) d) sets a to be (and b c), or’s result with d – You may assign as many variables as you want in a single setf statement by using var value pairs • (setf a 5 b 6 c 7)

More Assignments • To reassign a variable a new value, you use – (setf var (function using var)) as in • (setf x (+ 1 x)) – for simple increment/decrement reassignments, CL has a shortcut similar to Java/C, incf and decf • • (setf a (+ a 1)) = (incf a) (setf a (- a 1)) = (decf a) (setf a (+ a 10)) = (incf a 10) (setf a (- a b)) = (decf a b) • You can also use the if-else construct to create a conditional operator – in C or Java, we might have x = (y > z) ? y : z; – in CL it would be (setf x (if (> y z))

Other Assignment Statements • Setf is the preferred assignment statement because it can assign to any type of variable and to a location within a variable – arrays, strings (we cover this later in the semester) – car or cdr of a list as in (setf (car lis) ’a) • Here are some variations of assignment – setq can only assign to individual variables – psetq – multiple assignments happen in parallel • (setq a 5 b a) – assigns a to 5, b to a or 5 • (psetq a 5 b a) – assigns a to 5 and b to a’s old value (if a was uninitialized an error occurs) – set – used to select a variable to change • (set (if (> a b) `a `b) c) ; ; assigns the larger of a or b to c – in nearly any situation, you will want to use setf • Makeunbound – unbinds a variable • Fmakeunbound – unbinds a global variable – use these with caution, it might be better to assign a variable to nil

Two More • Not true assignment statements, but here are some interesting variations – rotatef to swap two values • the two values do not have to be the same type! – (setf a ’a) (setf b 5) (rotatef a b) b is now ’a and a is now 5 • (rotatef a b) is equivalent to (let ((tmp a)) (setf a b b tmp) nil) – shiftf left shifts a list of values • each value in the set of parameters is moved into the variable on its left, the leftmost variable’s value is returned – if a = 5, b = 6, c = 7 and d = 8, (shiftf a b c d 9) returns 5 with a = 6, b = 7, c = 8, d = 9 • if the rightmost item is a variable, it retains its original value • (shiftf a b c) would have a = b, b = c, and c unchanged, returning the old value of a

Parameters • Like variables in CL, parameters are also not declared by type (with a few exceptions) – However, they must be listed in your function definition so that their scope is determined • CL uses pass by copy, but all variables are pointers, so you can manipulate an item in memory using a destructive operation (we will cover what this means in more detail later) – When you write a function, you list the params in ( ) – When you call a function, you list the params after the function name, without ( ) – All params listed are required unless they are specified as optional (see the next slide), so here we see only mandatory params (defun foo (a b c) (if (= a b) c (+ a b c))) (foo 3 3 5) or (foo 1 2 3)

Optional Parameters • There are three ways to specify optional parameters – &optional • here, after &optional, you list extra params by name • the function can be called with any number of extra params, they are assigned to the list of optional params one by one • (defun foo (a &optional b c) …) – called with (foo 1 2) then a=1, b=2, c=nil – &key • the params listed after &key are keyword params, so that the calling unit specifies what value should be used for each param • (defun foo (a &key b c) …) – called with (foo 1 : c 3) – a=1, c=3, b=nil – &rest • similar to &optional, but here only one param name is used, any extra params are packaged into a list and passed into this &rest param • (defun foo (a &rest b) …) – called with (foo 1 2 3) – a = 1, b = (2 3)

Optional Parameter Examples • Here are some examples – (defun foo (a &optional b c d) (print (list a b c d))) • (foo 5 6 7) (5 6 7 nil) • (foo 5 6 7 8 9) error – (defun foo (a &rest b) (print (list a b))) • (foo 5 6) (5 (6)) • (foo 5) (5 nil) • (foo 5 6 7 8 9) (5 (6 7 8 9)) • Note: you can combine &optional, &rest and &key in certain orders, but the behavior may not be as expected – (defun foo (a &optional b c &rest d) (print (list a b c d))) • (foo 5) (5 nil nil) • (foo 5 6 7) (5 6 7 nil) • (foo 5 6 7 8 9) (5 6 7 (8 9)) – (defun foo (a &rest b &optional c d) …) • this yields an error since &rest cannot precede &optional (this would make no sense since &rest grabs all remaining params and places them in a list referenced by b

Atoms vs Lists • While a variable can point to either form, atoms and lists are very different, each having their own set of functions – Atoms are stand alone and atomic – Lists are embedded in ( ) and consist of at least one cons cell • cons cell permits the operations car and cdr • the cdr is a pointer so that many list functions use the pointer to go onto the next cons cell, or if nil the function terminates – There is no explicit declaration of variables as to their types, but be careful that you are using the right type for a given function or else you will get a runtime error • we will see functions to test if a variable is currently pointing to a list or an atom CDR CAR ’Hi CDR CAR we view the car as a pointer to the first item, but we can think of it in either way above

Operations on Atoms • Functions for atoms break into roughly five types: – Predicates • functions that test a datum and return T or nil – Numeric operations • such as +, -, *, /, mod, rem, log, exp, sin, cos, tan, floor, ceiling, round, truncate (note: mod and rem do the same thing) – Equality operations • eq, eql, equalp, = – Logical operations: not, and, or • and/or work on multiple items (2 or more) looking for items that are non-nil (rather than items that are only T) • or returns the first non-nil item rather than T • and/or are short-circuited • not returns T if the item is nil, or nil otherwise (if the item is non-nil) – Other (char operations, string operations, miscellany)

Some Atom Predicate Functions • Most predicate functions end in “p” • Here a group used to determine if a variable currently points to a given type – integerp, rationalp, floatp, complexp, characterp, stringp, vectorp, arrayp – return T or nil depending on whether the given argument is of that form – (integerp foo) – returns T if foo points to an integer, nil otherwise • typep – determine if a variable is currently pointing to a given type – (typep foo ’integer) – Note: you can determine the type of a variable by (type-of var) • symbolp and listp – is the item a symbol or a list? • consp – is the variable a cons cell? This differs from listp in that an empty list is still a list for listp, but not a cons cell for consp • atom, null – notice that these don’t end in p • functionp – test to see if an item is a function • zerop, plusp, minusp, evenp, oddp – these work only on numbers, the latter two only on integers

Equality Functions • eq – are two variables pointing to the same item in memory? – it is roughly equivalent to = = in Java when comparing objects – note that the outcome of this function is in part based on how CL is implemented • (eq 5 5) – may be T or nil, did the CL interpreter store 5 in two locations? • (setf a ’hi) (setf b ’hi) (eq a b) – may be T or nil • eql and = are for numbers – = compares two numbers and returns T if they are the same number – eql is stricter in that the two numbers must be the same type • (= 3 3. 0) is T but (eql 3 3. 0) is nil • note that = can take more than 2 arguments • equal – same as eq/= for atoms and numbers, but for lists, compares the elements of each list rather than memory locations – (eq ’(a b (c d))) is nil (they are not the same list in memory) – (equal ’(a b (c d))) is T • equalp is a case insensitive version of equal when comparing characters/strings

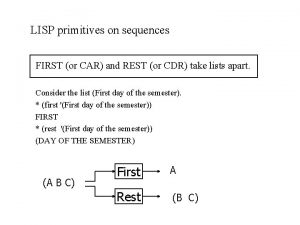
List Functions • There a great number of List functions – they break down into numerous categories including obtaining a given item, creating a list, joining multiple lists, set operations on lists, and destructively manipulating lists • Functions that return a value from a specified list location: – car, cdr • also combinations of car and cdr like cadr, caar, cddr, caadr, caddr, caaar, cdddr, etc • rest is the same as cdr • nthcdr performs cdr n times so (nthcdr 3 ’(1 2 3 4 5)) (4 5) – first, second, third, …, tenth are all defined • (first foo), (second foo), etc up to (tenth foo) – nth – general purpose function to get an item at a specified location as in (nth 5 foo) – note, lists start at location 0, so this would return the 6 th item of foo – reverse – return the entire list, but reversed

Assigning Into A List • Aside from retrieving items from a given location in a list, you can also directly assign data into a list by using setf and the previous operations (car, cdr, first, nth, etc) – – – (setf a ’(a b c)) a is (a b c) (setf (car a) ’d) a is now (d b c) (setf (cdr a) ’(e)) a is now (d e) (setf a ’(a b c d e)) (setf (third a) ’g) a is (a b g d e) (setf (rest a) ’(f g h)) a is (a f g h) • note: this does not work with setq or set – You should make sure that you assign cdr or rest of a list to a list, not an atom • (setf (rest a) i) a is (a. i) – a dotted pair, not a true list

Examples • (setf a ’(a b (c d e f) (g (h i j)) (k) (l (m n) o (p (q r))) s t)) – – – – – A (third a) (c d e f) B (car (third a)) c (C D E F) (cadr (third a)) d (G (H I)) (dolist (temp a) (print (temp)) (K) (L (M N) O (P (Q R))) (caddr a) c S (fourth a) (g (h i j)) T (nth 4 a) (k) NIL (cdddr a) ((g (h i j)) (k) (l (m n) o (p (q r))) s t)) (nth 1 (nth 3 (nth 5 a))) (q r) (setf (nth 2 a) ’c) c, this changes a to be (a b c (g (h i j)) (k) (l (m n) o (p (q r))) s t)) – (setf (cddr a) nil) nil, this changes a to be (a b) – (setf (cdr a) ’c) c, this changes a to be (a. c) – (setf (cdr a) nil) nil, this changes a to be (a)

List Creation Functions • The common way to create a list is with cons s – (cons f s) • cons creates a cons cell with the first pointer pointing at f and the second pointing at s f – We expect s to be a list or nil (or ’( )) • (cons ’a ’(b)) (a b) – If s is an atom, cons will create a dotted pair • (cons ’a ’b) (a. b) – To create a multi-item list, we need to embed or cons calls • (cons ’a (cons ’b (cons ’c nil))) (a b c) – Often, we will accomplish this through recursion instead (defun createlist ( ) (let ((temp (read))) (if (equal temp '!) (cons temp nil) (cons temp (createlist)))))

Cons Examples • (CONS ’A ’( ) ) – returns (A) A • (CONS ’A ’(B C)) – returns (A B C) • (CONS ’(A) ’(B)) – returns ((A) B) • (CONS ’A ’((B C))) – returns (A (B C)) In general, to build a list using cons, start with an atom and cons it to ’( ) (or nil) Cons another atom to what you got from above, etc Its easiest to build a list using cons by recursion so that the list created by the previous recursive call is the item being cons-ed onto by a new atom • (CONS ’(A B) ’(C D)) – returns ((A B) C D) C A B D

The List Function • cons is the preferred, but it is often difficult to work with, especially if you don’t like recursion – Another way to build a list is to use the list function, which takes items and groups them into a list – Items can be atoms or lists • but, you have to specify each individual item • and lists are inserted as sublists • (list ’a ’(b c)) (a (b c)) not (a b c) – List* can get around this problem because list* makes a “dotted pair” with the last cons cell f s • (list* ’a ’b ’(c d) (a b c d) • but (list* ’a ’b ’c ’d) (a b c. d) If s is a list, then this works out ok, otherwise you get f. s

Other List Creation Functions • Append – takes two (or more) lists and adds the second to the end of a list – (append ’(a b) ’(c)) (a b c) • does not work if any param is not a list • append actually can work with one param, but it doesn’t make any sense to do that as you get back the same list • Make-list – takes an int value and creates a list of that many items – initialized to nil unless you specify the initial element • (make-list 3) (nil nil) • (make-list 6 : initial-element ’a) (a a a a) • Copy-list – takes a list and creates a copy – this may be more desirable over append or cons because append and cons return pointers to the list(s) being manipulated (see next slide)

Example CL-USER 175 > (setf a '(1 2)) (1 2) CL-USER 182 > (setf c (append a b)) (1 2 3 4) CL-USER 176 > (setf b '(3 4)) (3 4) CL-USER 183 > (setf (car a) 5) 5 CL-USER 178 > (setf c (append a b)) (1 2 3 4) CL-USER 184 > a (5 2) CL-USER 179 > (setf (car c) 5) 5 CL-USER 185 > c (1 2 3 4) CL-USER 180 > c (5 2 3 4) CL-USER 181 > a (1 2) Notice that changing a or c has no impact on the other, but this will not necessarily be the case, for instance if we do this: (setf a ’(1 2 3 4)) (setf c (cdr a)) (setf (car c) 5) c is now (5 3 4) but a is now (1 5 3 4) so be careful when changing items in a list

Some Other List Functions • Some manipulation operations: – subst – returns a list with one item substituted for another • (subst ’a ’b ’(a b c b)) – returns the list (a a c a) – sublis – same as subst but the items specified can be sublists instead of atoms – remove – return a copy of the list with the given item removed • (remove 3 ’(1 2 3 4 5)) – returns (1 2 4 5) – removes all occurrences, there is also – remove-duplicates will return a list with all duplicate entries removed • More accessing functions: – butlast – return the list without the last item • (butlast x) = (reverse (cdr (reverse x))) – revappend – same as reverse followed by append • (revappend x y) = (append (reverse x y)) – ldiff – given a list and a sublist (the sublist must be a pointer into a part of the list), this returns the portion of list not in sublist • (setf a ’(a b c d e)) (setf b (cdr a))) (ldiff a b) returns (a b)

Using Lists for Other Types • Because Lists play such a central role in Lisp, some types do not have to be made available or implemented as ADTs – instead we can simulate them using lists • Stacks: – push – add to beginning of list (destructive) • (push item list) – pop – remove from beginning of list (destructive) • (pop list) – returns item at from of list and removes it from list – basically does (let (temp (first list))) (setf list (cdr list)) list) – pushnew – same as push but only adds the item if the item is not already present in the list • Queues: – to dequeue, use pop (destructive) – you can define enqueue as (defun enqueue (val lis) (append lis (list val))) • non-destructive, you would have to do (setf queue (enqueue val queue)) • Empty for both ADTs is simply testing the list against nil, and since we are using heap memory, we assume the ADT is never full • We can implement peak using car

Lists as Sets • Sets are also easy to implement using lists because of numerous built-in functions: – member – is a given item a member of the list? • (member ’a foo) returns either nil or the list starting at ’a • (setf a ’(a b c d e)), (member ’c a) (c d e) – recall that anything that is not nil is t, so member can be used as a predicate function – adjoin – adds an element to the front of the list if the element does not already occur in the list • (adjoin ’f a) (f a b c d e) but (adjoin ’c a) (a b c d e) – union, intersection • return the union or intersection of two lists – the return lists’ order is the second list reversed followed by the first list for union, second list reversed for intersection – set-difference, set-exclusive-or • destructive operations nunion, nintersection, nset-difference, nsetexclusive-or (we examine destructive operations in three slides)

Lists as Trees • Lists with sublists are a natural way to represent a general tree – (a (b (c d e) f (g h) i j (k l m n))) represents the tree to the right – basically a node’s children are placed in parens to the node’s right, in a recursive manner • we can access the children of a given node by taking the sublist of children and looking only for atoms, not lists • we can perform a depth-first traversal of the tree by visiting every node, one at a time from left to right in the list • to add a node to the tree, we have to find the right sublist and then add an atom to the list in the proper place (we could append it to the end, cons it to the beginning for simplicity) • to delete a node, we have to find the right sublist and remove the node – these operations are typically implemented recursively but some could be done iteratively making the tree implementation easier than in other languages

Lists as Tuples • Newer languages like Python are not providing arrays but instead are providing tuples – the items stored in the structure do not have to be the same type – the items can be indexed like any ordinary array – CL’s arrays are homogenous just like other languages, but lists do not have to be – (setf lis ’(a 3 “foo” #(1 2 3) 3. 1415 abc 3/5)) • lis consists of the symbol a, the int 3, the string “foo”, the array storing 1, 2 and 3, the float 3. 1415, the symbol abc and the fraction 3/5 • While the non-homogenous list is not a true tuple (you can’t reference items as if it were an array), we have list functions to simulate this – – (dolist (a lis) (print lis)) – prints out each element of the array (nth 2 lis) – returns “foo” (setf (nth 3 lis) nil) – removes the array from lis in favor of nil (dotimes (k (length lis)) (if (numberp (nth k lis)) (setf (nth k lis) 0))) • iterates through the list and replaces each number with 0

Destructive Operations • Many of the operations have destructive versions – the original list will not remain intact • nconc – concatenates two lists – returns the new list and alters the first to be the concatenation • reverse returns a copy of the list reversed, original list remains the same • nreverse is the same as reverse but alters the original list – (setf a ’(a b c d)) – (reverse a) returns (d c b a) with a being (a b c d) – (nreverse a) returns (d c b a) with a being (a) • nreconc – combines nreverse followed by nconc • (setf a ’(a b c d)) and (setf b ’(a c g h)) – (intersection a b) returns (c a) with a and b unchanged – (nintersection a b) returns (c a) but now a is (a), b is unchanged • (setf a ’(a b c d)) and (setf b ’(a c g h)) – (union a b) returns (h g a b c d) with a and b unchanged – (nunion a b) returns (h g a b c d) with a unchanged but b is (a c g a b c d)

More on Destructive Operations • Because changing the car and cdr of a list is common, a shortcut approach is to use rplaca and rplacd – – (setf a ’(a b c d e)) (rplaca a ’f) (f b c d e) with a changed to this list (rplacd a ’(g h)) (f g h) with a changed to this list (rplacd a ’i) (f. i) with a changed to this list • Other destructive functions include – nsubst, nsublis – nstring-capitalize, nstring-upcase, nstring-downcase • these alter the characters in strings as you might have guessed – nbutlast • Destructive functions are dangerous for two reasons – you are destroying data as a side effect of a function, usually you don’t expect functions to have side effects – the new list may not reflect the data in the order that you might expect – use destructive functions with caution, or use the non-destructive versions and set a new variable to the return of the function as is needed • For instance, instead of doing (nbutlast a), do (setf b (butlast a))

Other Types of Data • Believe it or not, we have only scratched the surface regarding data types in CL – characters – we can store, manipulate and test characters (note: these are characters like what we find in Java, these are NOT symbols) – sequences – a general category of homogenous container, there are built -in functions for sequences and then more specific functions for some of the specific classes: • strings – are really arrays of characters, but there are built-in string functions available to make it easier to do things like capitalize the letters, compare strings, etc • arrays – arrays are typed and can include bit arrays • hash tables – to create dictionary-type of structures – similar to C’s structs, there are numerous built-in operations available – objects/classes – added to CL is the Common Lisp Object System (CLOS), which provides classes on par with C++ – streams – for input and output • We will explore all of these later in the semester
- Slides: 36