Variable Length Coding Information entropy Huffman code vs

Variable Length Coding § Information entropy § § § § Huffman code vs. arithmetic code Arithmetic coding Why CABAC? Rescaling and integer arithmetic coding Golomb codes Binary arithmetic coding CABAC VLC 2009 PART 1 <>

Information Entropy § Information entropy: Claude E. Shannon 1948, “A Mathematical Theory of Communication” § The information contained in a statement asserting the occurrence of an event depends on the probability p(f), of occurrence of the event f. - lg p(f) § The unit of the above information quantity is referred as a bit, since it is the amount of information carried by one (equally likely) binary digit. § Entropy H is a measure of uncertainty or information content - Very uncertain high information content VLC 2009 PART 1 <>

Entropy Rate § Conditional entropy H(F|G) between F and G: uncertainty of F given G § Nth order entropy § Mth order conditional entropy § Entropy rate (lossless coding bound) VLC 2009 PART 1 <>

Bound for Lossless Coding § Scalar coding: could differ from the entropy by up to 1 bit/symbol § Vector (block) coding: assign one codeword for each group of N symbols § Conditional coding (predictive coding, context-based coding): The codeword of the current symbol depends on the pattern (context) formed by the previous M symbol VLC 2009 PART 1 <>

Huffman Coding • Huffman coding for pdf: (a 1, a 2, a 3) = (0. 5, 0. 25) – –lg 0. 5 = 1, –lg 0. 25 = 2 a 1 = 0. 5 0 1 – a 1 = 0, a 2 = 10, a 3 = 11 0 a 2 = 0. 25 1 a 3 = 0. 25 • If the self information is not integer? – pdf: (a 1, a 2, a 3, a 4) = (0. 6, 0. 2, 0. 125, 0. 075) – –lg 0. 6 = 0. 737, –lg 0. 2 = 2. 32, 0 –lg 0. 125 = 3, –lg 0. 075 = 3. 74 1 a 1 = 0. 6 1 – a 1 = 0, a 2 = 10, a 3 = 110, a 4 = 111 2021/3/2 VLC 2009 PART 1 a 2 = 0. 2 0 0 a 3 = 0. 125 1 a 4 = 0. 075 H 1=1. 5617 R 1=1. 6 <5>

Huffman vs. Arithmetic Coding § Huffman coding: convert a fixed number of symbols into a variable length codeword § Efficiency § The usage of fixed VLC tables does not allow an adaptation to the actual symbol statistics. § Arithmetic Coding: convert a variable number of symbols into a variable length codeword § Efficiency § Process one symbol at a time § Easy to adapt to changes in source statistics § Integer implementation is available VLC 2009 PART 1 <>

Arithmetic Coding • The bits allocated for each symbol can be non-integer – If pdf(a) = 0. 6, then the bits to encode ‘a’ is 0. 737 • For the optimal pdf, the coding efficiency is always better than or equal to the Huffman coding • Huffman coding for a 2 a 1 a 4 a 1 a 3, total 11 bits: 2 + 1 + 3 • Arithmetic coding for a 2 a 1 a 4 a 1 a 3, total 11. 271 bits: 2. 32 2021/3/2 +0. 737+ 3. 74 +0. 737+ VLC 2009 PART 1 3 <7> The exact probs are preserved

Arithmetic Coding • Basic idea: – Represent a sequence of symbols by an interval with length equal to its probability – The interval is specified by its lower boundary (l), upper boundary (u) and length d (= probability) – The codeword for the sequence is the common bits in binary representations of l and u • The interval is calculated sequentially starting from the first symbol – The initial interval is determined by the first symbol – The next interval is a subinterval of the previous one, determined by the next symbol 2021/3/2 VLC 2009 PART 1 <8>

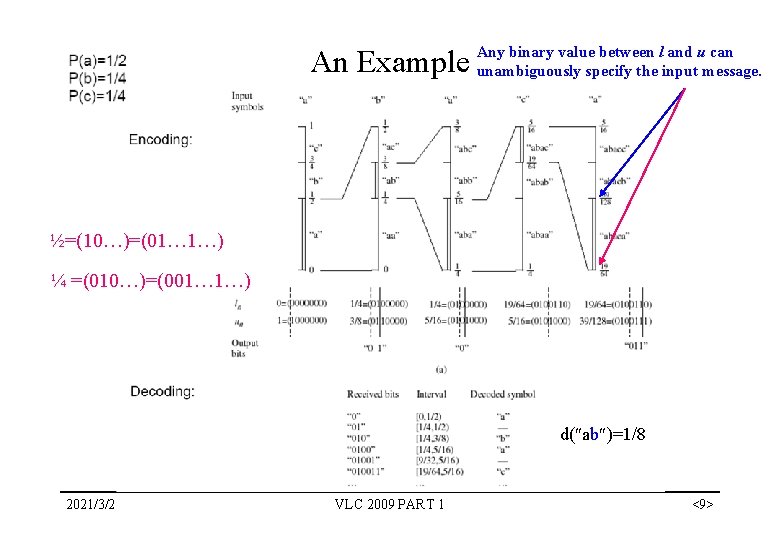
binary value between l and u can An Example Any unambiguously specify the input message. ½=(10…)=(01… 1…) ¼ =(010…)=(001… 1…) d( ab )=1/8 2021/3/2 VLC 2009 PART 1 <9>

Why CABAC? § The first standard that uses arithmetic entropy coder is given by Annex E of H. 263 § Drawbacks: 1. Annex E is applied to the same syntax elements as the VLC elements of H. 263 2. All the probability models are non-adaptive that their underlying probability as assumed to be static. 3. The generic m-ary arithmetic coder used involves a considerable amount of computational complexity. VLC 2009 PART 1 <>

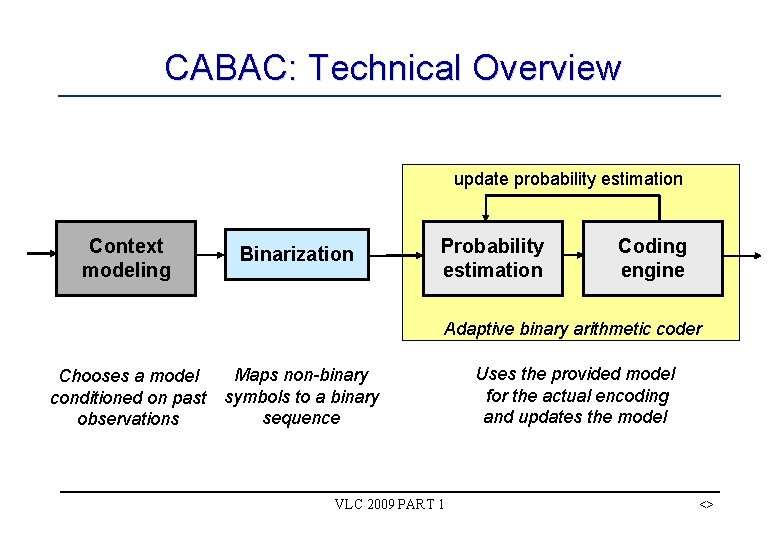
CABAC: Technical Overview update probability estimation Context modeling Binarization Probability estimation Coding engine Adaptive binary arithmetic coder Maps non-binary Chooses a model conditioned on past symbols to a binary sequence observations VLC 2009 PART 1 Uses the provided model for the actual encoding and updates the model <>

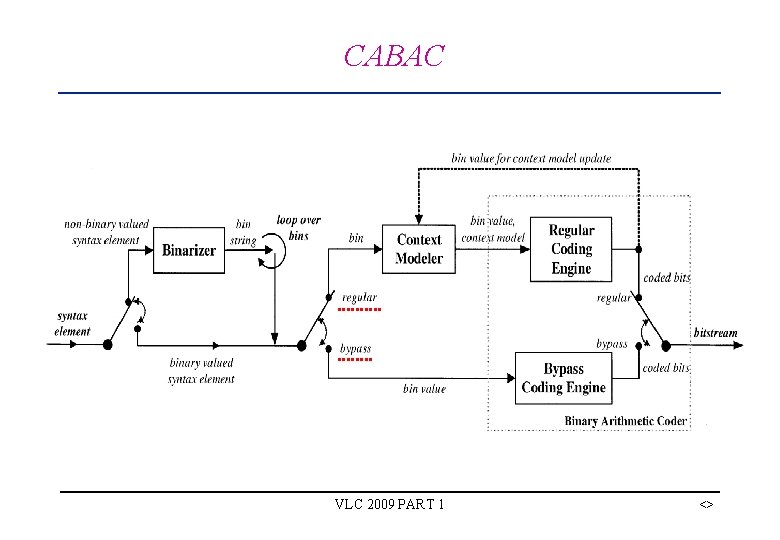
CABAC VLC 2009 PART 1 <>

Context-based Adaptive Binary Arithmetic Code (CABAC) § Usage of adaptive probability models § Exploiting symbol correlations by using contexts § Non-integer number of bits per symbol by using arithmetic codes § Restriction to binary arithmetic coding • Simple and fast adaptation mechanism • But: Binarization is needed for non-binary symbols • Binarization enables partitioning of state space VLC 2009 PART 1 <>

Implementation of Arithmetic Coding § Rescaling and Incremental coding § Integer arithmetic coding § Binary arithmetic coding § Hoffman Trees § Exp-Golomb Codes VLC 2009 PART 1 <>

Issues § Finite precision (underflow & overflow): As n gets larger, these two values, l(n) and u(n) come closer and closer together. This means that in order to represent all the subintervals uniquely we need to increase the precision as the length of the sequence increases. § Incremental transmission: transmit portions of the code as the sequence is being observed. § Integer implementation VLC 2009 PART 1 <>

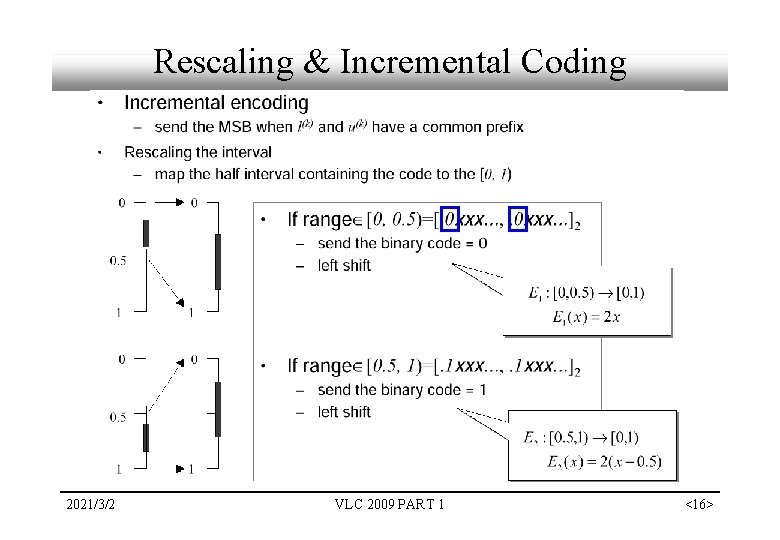
Rescaling & Incremental Coding 2021/3/2 VLC 2009 PART 1 <16>

Incremental Encoding U U L L L U 2021/3/2 VLC 2009 PART 1 <17>

Question for Decoding § How do we start decoding? decode the first symbol unambiguously § How do we continue decoding? mimic the encoder § How do we stop decoding? VLC 2009 PART 1 <>

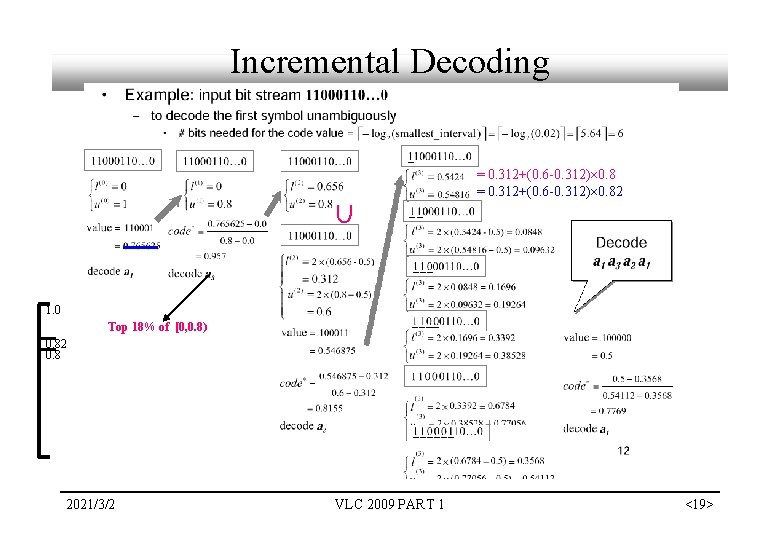
Incremental Decoding U = 0. 312+(0. 6 -0. 312) 0. 82 1. 0 Top 18% of [0, 0. 8) 0. 82 0. 8 2021/3/2 VLC 2009 PART 1 <19>

Issues in the Incremental Coding 2021/3/2 VLC 2009 PART 1 <20>

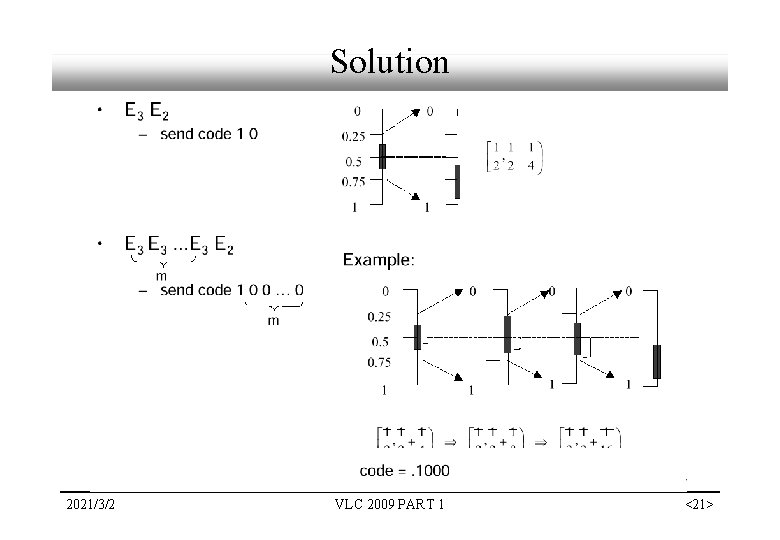
Solution 2021/3/2 VLC 2009 PART 1 <21>

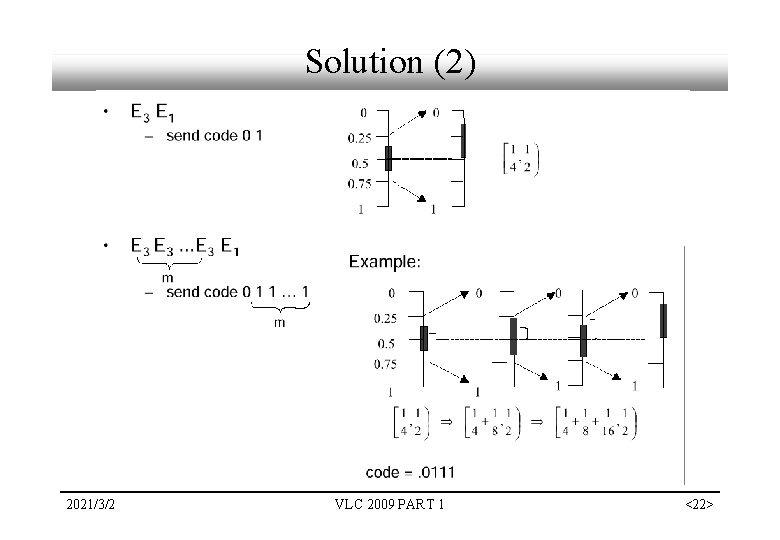
Solution (2) 2021/3/2 VLC 2009 PART 1 <22>

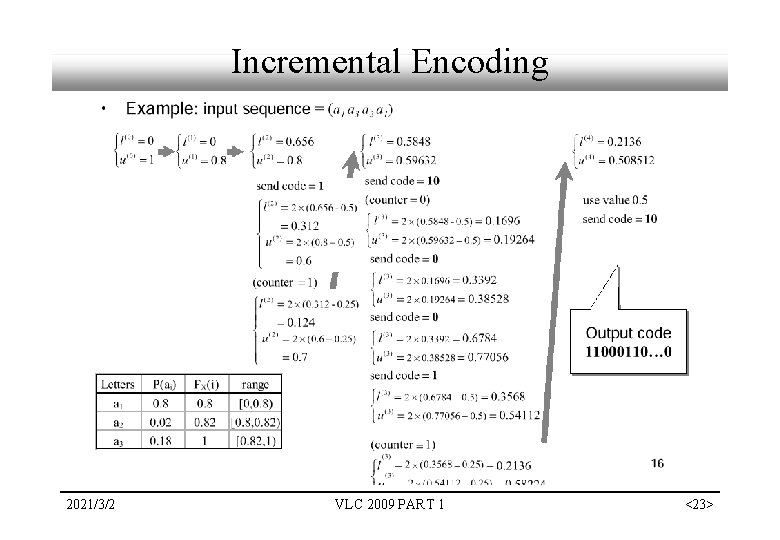
Incremental Encoding 2021/3/2 VLC 2009 PART 1 <23>

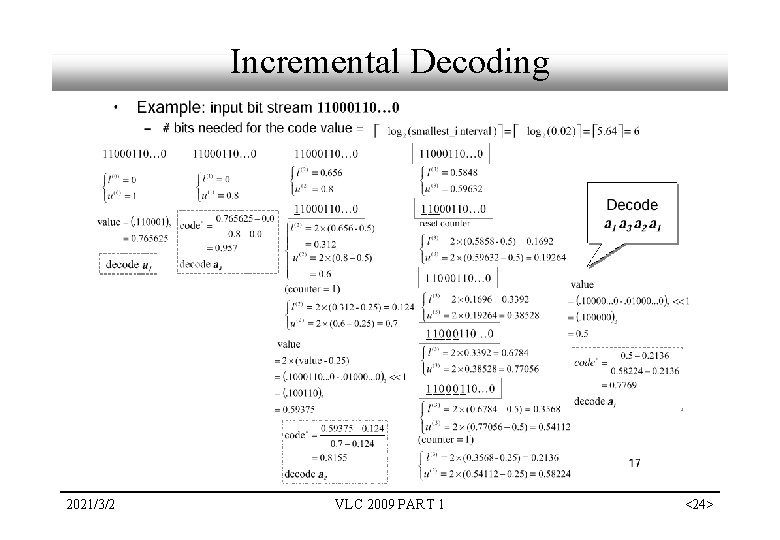
Incremental Decoding 2021/3/2 VLC 2009 PART 1 <24>

Integer Implementation -1 2021/3/2 VLC 2009 PART 1 <25>

Integer Implementation • nj: the # of times the symbol j occurs in a sequence of length Total Count. • FX(k) can be estimated by • Define we have • E 3: if (E 3 holds) Shift l to the left by 1 and shift 0 into LSB Shift u to the left by 1 and shift 0 into LSB Complement (new) MSB of l and u Increment Scale 3 2021/3/2 VLC 2009 PART 1 <26>

Golomb Codes § Golomb-Rice code: a family of codes designed to encode integers with the assumption that the larger an integer, the lower its probability of occurrence. § An example (the simplest, unary code): for integer n, codes as n 1 s followed by a 0. This code is the same as the Huffman code for {1, 2, …} with probability model § Golomb code with m: code n > 0 using two numbers q and r: § Q is coded by unary code of q; r is represented by binary code using bits. n q r code § the first – m values, uses bits 0 000 5 1 0 1000 § the rest values: use + 1 bits 1 001 6 1 1 1001 2 010 7 1 2 1010 § Golomb code for m = 5: 3 0110 8 1 3 10110 3+3=110 4 0111 VLC 2009 PART 1 9 1 4 10111 <>

Golomb Codes § Golomb code is optimal for the probability model § exp-Golomb code: variable length codes with regular construction: [m zeros] [1] [info]. code_num: index info: is an m-bit field carrying information § Mapping types: ue, te, se, and me § designed to produce short codewords for frequently-occurring values and longer codewords for less common parameter values. VLC 2009 PART 1 <>

exp-Golomb Codes § exp-Golomb code the group size increases exponentially § Decode: 1. Read in m leading zeros followed by 1. 2. Read m -bit info field. 21 -2 3. � m zeros�� 1�� info� 22 -2 23 -2 VLC 2009 PART 1 <>

exp-Golomb Entropy Coding A parameter k to be encoded is mapped to code_num in one of the following ways: 2021/3/2 VLC 2009 PART 1 <30>

exp-Golomb Entropy Coding 2021/3/2 VLC 2009 PART 1 <31>

H. 264 Coding Parameters 2021/3/2 VLC 2009 PART 1 <32>

Uniqueness and Efficiency of AC(1) -log 2 p(x) VLC 2009 PART 1 <>

Uniqueness and Efficiency of AC(2) VLC 2009 PART 1 <>

Uniqueness and Efficiency of AC(3) VLC 2009 PART 1 <>

Uniqueness and Efficiency of AC(4) VLC 2009 PART 1 <>