VARIABEL ACAK RANDOM VARIABLES Fungsi yang dihubungkan dengan

VARIABEL ACAK (RANDOM VARIABLES) � Fungsi yang dihubungkan dengan suatu percobaan, yang nilai-nilainya adalah bilangan nyata dan kemunculan nilai-nilai tersebut bergantung pada peluang. � Variabel acak biasa dinotasikan dengan huruf besar bercetak tebal, misalnya: X, Y, Z, dsb.

DISTRIBUSI PELUANG SUATU VARIABEL ACAK DISKRIT Himpunan pasangan terurut (x, f(x)) dikatakan suatu distribusi peluang/fungsi peluang dari suatu variabel acak diskrit X jika memenuhi 3 kriteria berikut: � x f(x) 0 � x P(X=x) = f(x) � f(x) = 1 x

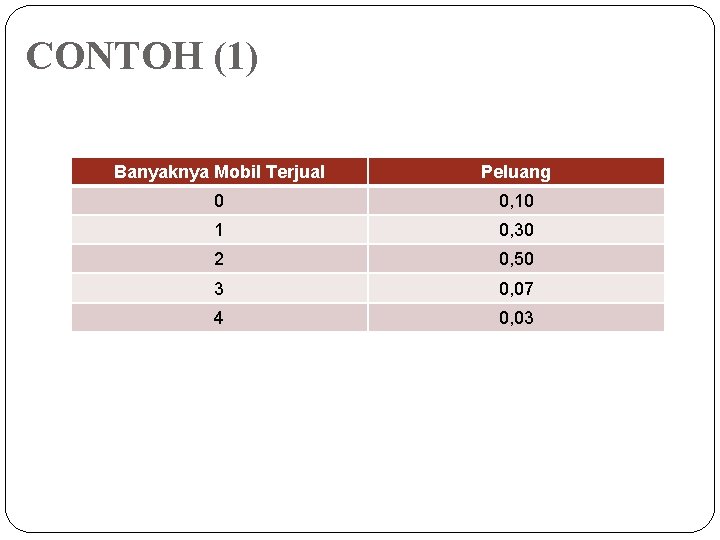
CONTOH (1) Banyaknya Mobil Terjual Peluang 0 0, 10 1 0, 30 2 0, 50 3 0, 07 4 0, 03

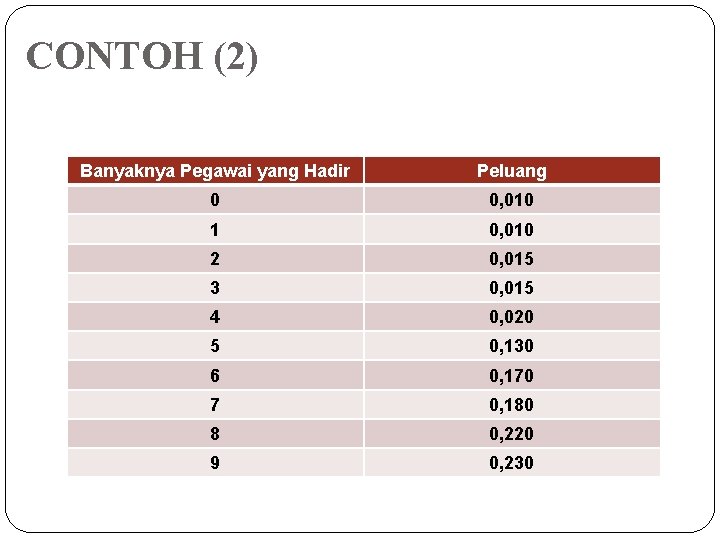
CONTOH (2) Banyaknya Pegawai yang Hadir Peluang 0 0, 010 1 0, 010 2 0, 015 3 0, 015 4 0, 020 5 0, 130 6 0, 170 7 0, 180 8 0, 220 9 0, 230

CONTOH (3) Misalkan 3 buah uang logam dilemparkan bersamaan dan variabel acak X menyatakan banyaknya sisi Angka yang muncul. �X dapat bernilai 0, 1, 2, 3 �P(X=0) = 1/8 P(X=1) = 3/8 P(X=2) = 3/8 P(X=3) = 1/8

MENENTUKAN FUNGSI PELUANG PADA CONTOH 3 S = {AAA, AAG, AGA, GAA, AGG, GGA, GAG, GGG} => |S| = 8 E 0 = {GGG} => |E 0| = 1 => P(E 0) = 1/8 E 1 = {AGG, GGA, GAG} => |E 1| = 3 => P(E 1) = 3/8 E 2 = {AAG, AGA, GAA} => |E 2| = 3 => P(E 2) = 3/8 E 3 = {AAA} => |E 3| = 1 => P(E 3) = 1/8

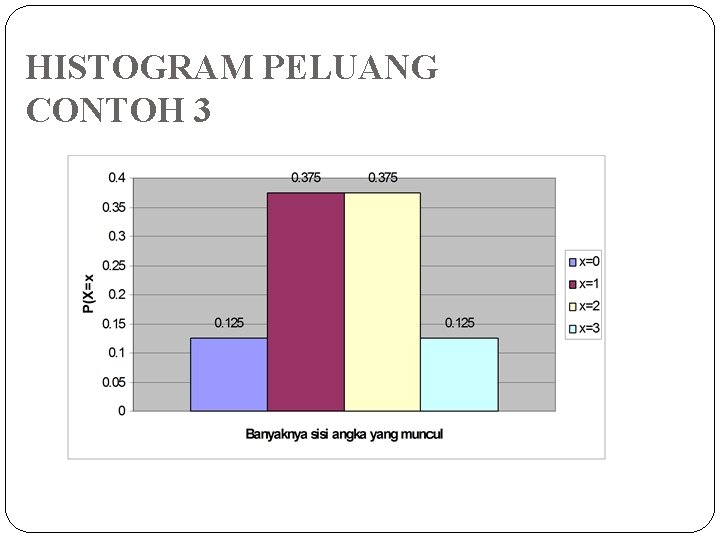
HISTOGRAM PELUANG CONTOH 3

RATA-RATA SUATU VARIABEL ACAK DISKRIT Misalkan X adalah suatu variabel acak diskrit dengan fungsi peluang f(x). Yang dimaksud dengan rata-rata/mean atau nilai harapan dari X adalah: X = E(X) = xf(x) x

CONTOH SOAL MENGHITUNG RATA-RATA Banyaknya mobil per hari bervariasi, dengan distribusi peluang berikut: P(X=0) = 0, 1 P(X=1) = 0, 15, P(X=2) = 0, 20, P(X=3) = 0, 25, P(X=4)=0, 3, dengan X adalah banyaknya mobil yang dicuci per hari. Berapakah rata-rata banyaknya mobil yang dicuci per hari?

JAWABAN �Rata-rata banyaknya mobil yang dicuci: E(X) = 0. 0, 1 + 1. 0, 15 + 2. 0, 20 + 3. 0, 25 + 4. 0, 30 = 0+0, 15+0, 40+0, 75+1, 20=2, 50. �Rata-rata penghasilan per hari = 2, 5 x Rp 15. 000 = Rp 37. 500.

MENENTUKAN RATA-RATA PADA CONTOH 3 �E(X) = 0. 1/8 + 1. 3/8 + 2. 3/8 + 3. 1/8 = 1, 5. �Rata-rata banyaknya sisi Angka yang muncul pada pelemparan 3 buah uang logam secara bersamaan adalah 1, 5.

Latihan 1 The Pizza Palace offers three sizes of cola – small, medium, and large - to go with its pizza. The colas are sold for $0. 80, $0. 90, and $1. 20, respectively. Thirty percent of the orders are for small, 50% are for medium, and 20% are for the large sizes. Organize the size of the colas and the probability of a sale into a probability distribution. Compute the mean amount charged for a cola.

Latihan 2 The information below is the number of daily emergency service calls made by the volunteer ambulance service of Walterboro, South Carolina, for the last 50 days. Number of Calls 0 1 2 3 4 SUM Frequenc y 8 10 22 9 1 50 Convert this information on the number of calls to a probability distribution. What is the mean number of emergency calls per day?

RATA-RATA PENDAPATAN SUATU JENIS TARUHAN (A) � Pelemparan 3 uang logam bersamaan � Bentuk taruhan: Apakah ketiga uang logam yang dilempar bersamaan menunjukkan sisi yang sama (Angka semua atau Gambar semua)? � Kalau muncul Angka semua atau Gambar semua kita mendapatkan Rp 80. 000. Kalau ada sisi yang tidak sejenis kita membayar Rp 30. 000 � Berapa rata-rata pendapatan dari taruhan tsb. ?

VARIANSI DAN SIMPANGAN BAKU SUATU VARIABEL ACAK DISKRIT Misalkan X suatu variabel acak diskrit dengan fungsi peluang f(x) dan rata-rata . Variansi dari X didefinisikan sebagai berikut: 2 X = E[(X - )2] = (x - )2 f(x) Akar positif dari variansi, X , disebut simpangan baku dari X.

TARUHAN B �Bentuk taruhan: Sebuah uang logam dilemparkan satu kali. Apakah akan muncul sisi Angka atau sisi Gambar? �Kalau muncul sisi Angka, kita mendapat Rp 60. 000. Kalau muncul sisi Gambar, kita membayar Rp 60. 000.

TARUHAN C �Bentuk taruhan: Sepasang dadu dilemparkan satu kali. Apakah kedua buah dadu menunjukkan jumlah mata dadu yang sama? �Kalau sama, kita mendapat Rp 60. 000. Kalau berbeda, kita membayar Rp 12. 000.

ANALISIS TARUHAN B �Misalkan variabel acak X menyatakan hasil yang kita dapatkan. �E(X) = 0, 5. Rp 60000 + 0, 5. (-Rp 60000) = 0 (taruhan yang adil) � 2 X = 0, 5. (Rp 60000 -0)2+0, 5. (-Rp 60000 -0)2 = (Rp 60000)2 � X = Rp 60000

ANALISIS TARUHAN C � Misalkan variabel acak X menyatakan hasil yang kita dapatkan. � E(X) = 1/6 Rp 60000 + 5/6 (-Rp 12000) = 0 (taruhan yang adil) � 2 X =1/6 (Rp 60000 -0)2+ 5/6 (-Rp 12000 -0)2 = 1/6 (Rp 60000)2 + 1/30 (Rp 60000)2 = 1/5 (Rp 60000)2 � X = Rp 26830