Vapor pressure and liquids Vapor A gas that

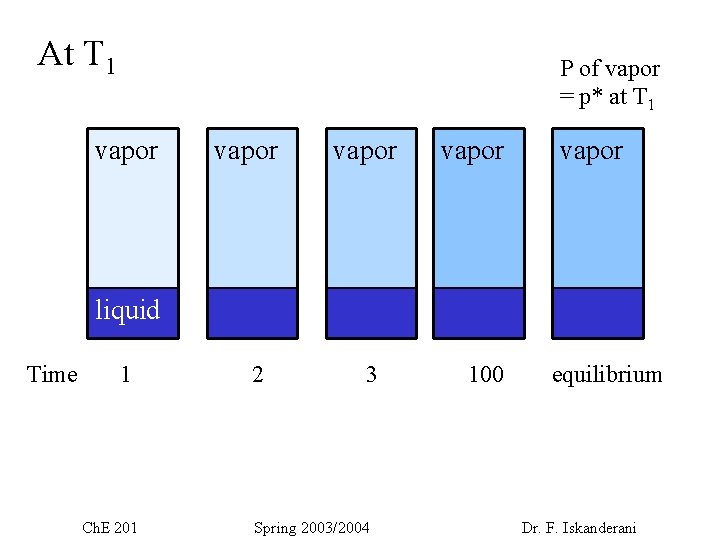
Vapor pressure and liquids Vapor : A gas that exists below its critical point Gas : gas that exists above its critical point Note : A gas can not condense in the process • If we have some liquid ( say water) in a closed container at some T 1 , then after some time, some vapor will exist above the liquid. This vapor will reach equilibrium (with the liquid). The vapor will have a pressure = vapor pressure, p 1* (at the given temp T 1). Note the vapor pressure is the maximum pressure the vapor can attain. Ch. E 201 Spring 2003/2004 Dr. F. Iskanderani

At T 1 P of vapor = p* at T 1 vapor vapor liquid Time 1 Ch. E 201 2 3 Spring 2003/2004 100 equilibrium Dr. F. Iskanderani

Vapor pressure and liquids Now change the temp to a higher temperature T 2. The system will reach equilibrium , and the vapor will have a new vapor pressure , p 2* > p 1* At T 1 At T 2 vapor Liquid At equilibrium, vapor will reach p 1* Ch. E 201 Spring 2003/2004 At equilibrium, vapor will reach p 2* Dr. F. Iskanderani

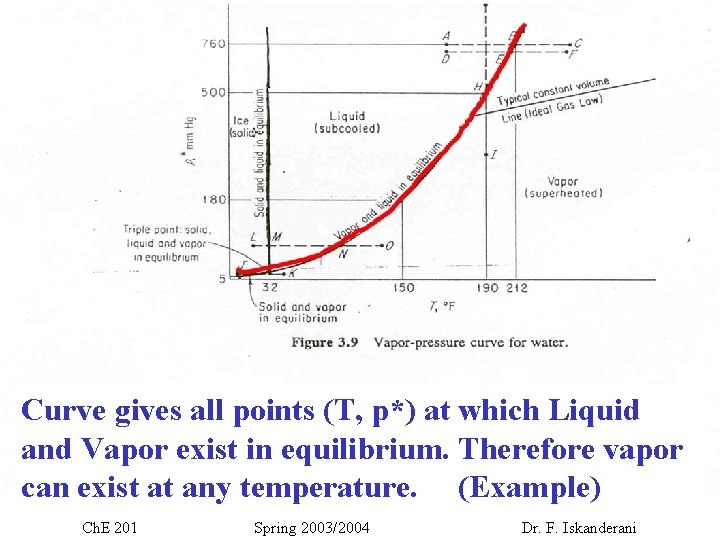
Curve gives all points (T, p*) at which Liquid and Vapor exist in equilibrium. Therefore vapor can exist at any temperature. (Example) Ch. E 201 Spring 2003/2004 Dr. F. Iskanderani

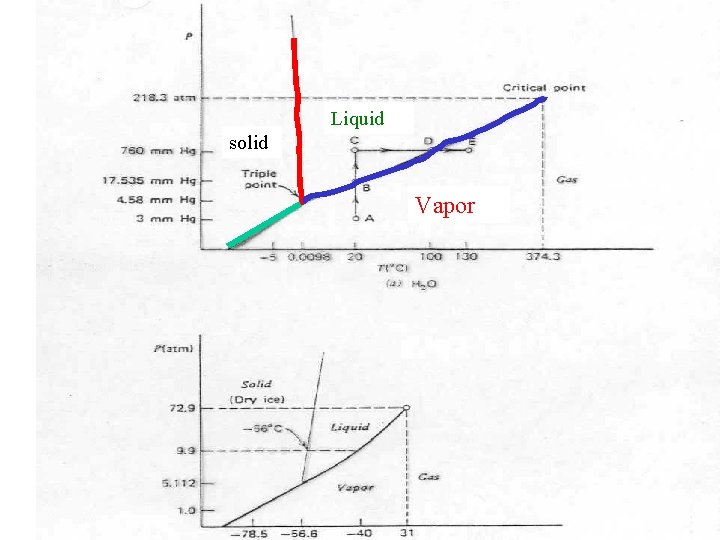
Liquid solid Vapor

Change of Vapor pressure with Temperature • p* vs T is a curve ( It is not a straight line) • A plot of ln p* vs 1/T for moderate temperatures 1 linear ln p* =m ( )+b T • Another form of this eq is the Antoine Equation ln p* =( . A. T+C ) +B (See appendix G on page 669) • the vapor pressure can be found from tables, charts or empirical equations (the Antoine equation) V – nb + Ch. E 201 Spring 2003/2004 Dr. F. Iskanderani

Change of vapor pressure with pressure Vl d(p*) =V g – nb +nd. P T T Under normal conditions the effect of P on the vapor pressure, p* is small Ch. E 201 Spring 2003/2004 Dr. F. Iskanderani

Liquid Properties • Liquid mixtures are more complex than gases • P V T behaviour prediction is difficult • If we can assume liquids are ideal liquids, then: V avg = V 1 x 1 + V 2 x 2 +. . • This eq is good for components with similar structure such as hydrocarbons Ch. E 201 Spring 2003/2004 Dr. F. Iskanderani

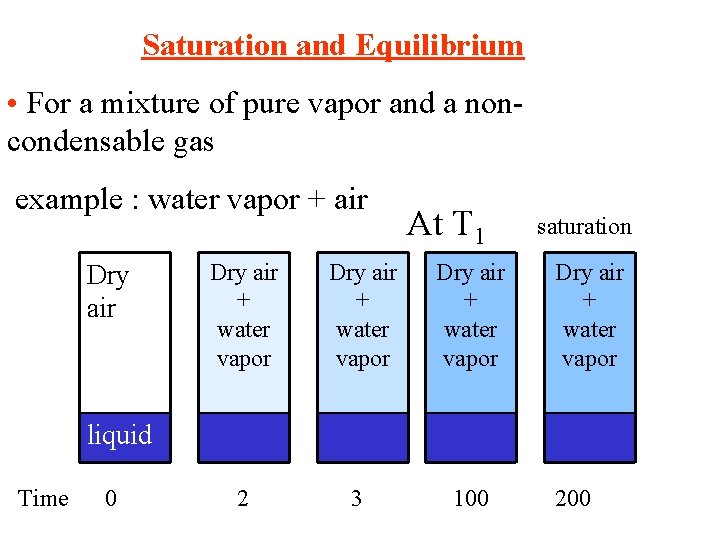
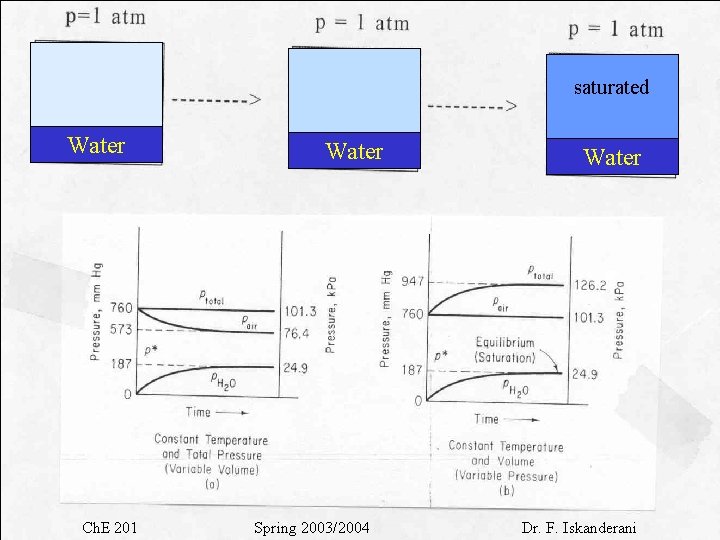
Saturation and Equilibrium • For a mixture of pure vapor and a noncondensable gas example : water vapor + air Dry air At T 1 Dry air + water vapor 2 3 100 saturation Dry air + water vapor liquid Time 0 200

• Water vaporizes until equilibrium at T 1 is reached. • At any condition before saturation, the vapor is partially saturated and its partial pressure is < p* • At saturation, air is fully saturated with the vapor and the partial pressure of the vapor is = p* Total pressure of gas mixture = pair + pwater vapor At saturation Ptotal = pair + p*water vapor When the mixture of gas and vapor is at saturation, we say thast the mixture is at the dew point Q: If we lower the temperature, what will happen? A: The vapor will condense

Dew point for a mixture of pure vapor and a noncondensable gas is the temp at which the vapor just starts to condense if cooled at constant pressure P = 1 atm, T= 65 o. C Dry air Inject some liquid water Dry air + vapor Water liquid When the air is fully saturated with the vapor, the partial pressure of the vapor = p* = Ch. E 201 Spring 2003/2004 Dr. F. Iskanderani

saturated Water Ch. E 201 Water Spring 2003/2004 Water Dr. F. Iskanderani

If ideal gas holds, then: (Dalton’s Law) pair V = nair R T pw V = nw R T Remember : ptot=pw+ pair and ntot= nw+nair OR if we take the vapor as 1 and the gas as 2: p 2 V = n 2 R T ……. (1) p 1 V = n 1 R T ……. . (2) ptot= p 1 + p 2 and ntot= n 1 + n 2 p 2= ptot – p 1 and n 2= ntot - n 1 Divide eq (2) by (1) p 1 = n 1 & p 1 = n 1 p 2 n 2 ptot ntot

At saturation : p w = p w* And the equations also hold Ch. E 201 Spring 2003/2004 Dr. F. Iskanderani

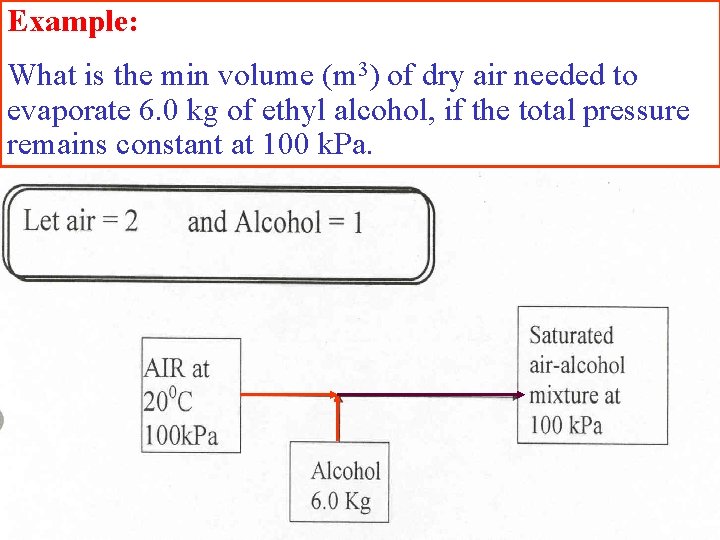
Example: What is the min volume (m 3) of dry air needed to evaporate 6. 0 kg of ethyl alcohol, if the total pressure remains constant at 100 k. Pa.

Remember : ptot=p 1+ p 2 and ntot= n 1+n 2 Therefore, 2. 07 kgmol of dry air at 20 o. C and 100 k. Pa, has a volume of: Then n 2 = 2. 07 kgmol V = 2. 07 x 8. 314 x 293 100

O 2 theoretically required = 9. 5 gmoles To calculate O 2 entering: ( Note: air is saturated with the vapor) n. O 2

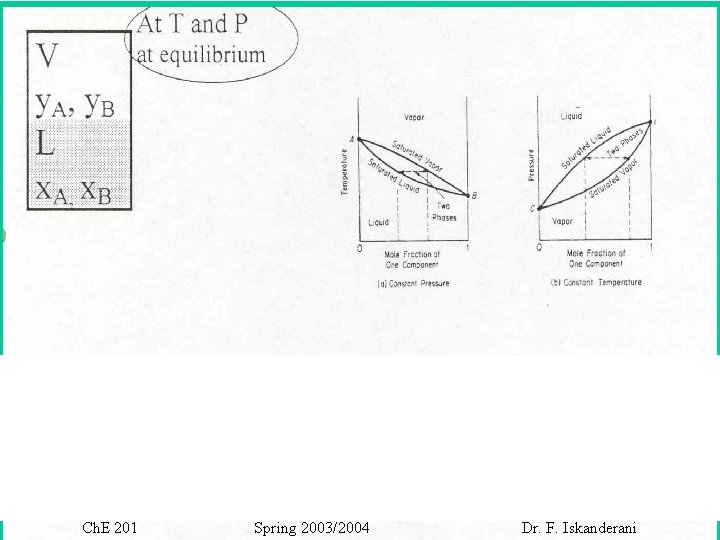
Vapor-Liquid Equilibria for Multicomponent Systems • Use Raoult’s Law and Henry’s Law to predict the partial pressure of a solute and a solvent. • List typical problems that involve the use of equilibrium coefficient Ki • We have 2 components A and B present in 2 phases ( V & L). At equilibrium, A in the liquid phase is in equilibrium with A in the Vapor phase. Equilibrium is a function of T, P composition Ch. E and 201 Spring 2003/2004 of the mixture. Dr. F. Iskanderani

Ch. E 201 Spring 2003/2004 Dr. F. Iskanderani

Henry’s Law : p. A= HA x. A ( Good for xi 0) ptot = p. A + p. B , Then: y. A= p. A/ptot = HA x. A/ptot and y. B= p. B/ptot = HB x. B/ptot Raoult’s Law: (Good for x. A 1) p. A = p. A*. x. A and p. B = p. B*. x. B where p. A+p. B=ptot Again, yi=pi/ptot THEN, Ki = yi/xi = pi*/ptot where Ki is the equilibrium constant Ch. E 201 Spring 2003/2004 Dr. F. Iskanderani

Typical problems that involve the use of the equilibrium constant Ki ( Note : These cases will be studied in detail in the Separation Processes I course next year) 1. Calculate the bubble point temperature of a liquid mixture given the total pressure and liquid composition 2. Calculate the dew point temperature of a liquid mixture given the total pressure and vapor composition Ch. E 201 Spring 2003/2004 Dr. F. Iskanderani

Typical problems that involve the use of equilibrium constant Ki 3. Calculate the related equilibrium V-L compositions over a range of mole fractions from 0 to 1 as a function of T given the total pressure 4. Calculate the composition of the V and L streams and their respective quantities when a liquid of a given composition is partially vaporized at a given T and P Ch. E 201 Spring 2003/2004 Dr. F. Iskanderani

The Phase Rule ( for systems in equilibrium only) F = C - P + 2 , where: P = number of phases that can exist in the system C = number of components in the system F = number of degrees of freedom (i. e. , number of independent properties to be specified to determine all the intensive properties of each phase Examples: Ch. E 201 Spring 2003/2004 Dr. F. Iskanderani