Values for matrices Determinant calculation Journal 5 Matrices

Values for matrices Determinant calculation

Journal 5 • Matrices can be used to present a variety of data. You can compare, solve, etc. with the data. • List five different jobs that would use a matrix and how you think they would use the matrix.

Determinant values • Matrices can have a numerical value associated with them • This value can be used to find an inverse matrix (used to solve systems of equations) • Positive could mean making money – spending money • Negative could mean losing money – costs of project

• Must have a square matrix to get a numerical value • 2 x 2, 3 x 3, 4 x 4, 5 x 5, etc. • We will deal with 2 x 2 and 3 x 3 only

2 x 2 matrix determinant value • For a 2 x 2 matrix: • The calculation for the value is the top diagonal numbers multiplied together then the bottom diagonal numbers are multiplied together. Subtract: top – bottom • The answer cannot be zero – no value

Calculation • Top diagonal = ad • Bottom diagonal = bc • Answer: ad - bc

examples

3 x 3 matrix determinant • A 3 x 3 matrix will have three sets of top diagonals and three sets of bottom diagonals • In order to get the sets, you have to expand the matrix • Original 3 x 3 expanded 3 x 3 • re-write columns 1 and 2

• Top diagonals – multiply each set, then add the three answers together • aei + bfg + cdh

• Bottom diagonals – multiply each set, then add the three answers together • gec + hfa + idb

Final answer • Top sum – bottom sum • This is the value for the determinant

examples • expand

• expand

• expand

assignment • Worksheet on calculating determinant values

Journal 6 • Getting a determinant value can tell you a value that can be interpreted for a specific outcome. • Explain why a positive determinant value could be both good and bad for a project. • Explain why a negative determinant value could be both good and bad for a project.

• Matrices are a way to organize thoughts and data for display and for manipulation. • Scalar multiplication can be used for manipulation (number times to matrix)

Applications • Matrices can be used to calculate the area of a triangle from a set of points • 1/2 base*height • Need three points – then to be a square matrix, there will be a one placed in the last column • Area cannot be negative, the answer is always an absolute value of the matrix

formula • Taken from the points: • You will still evaluate using an expanded matrix

Examples: expanded matrix • Points: (2, 3), (4, 1), (5, 2)

• Points: (0, 1), (4, 5), (-2, 4)

worksheet • Calculate the area using the matrix formula for the area of a triangle • Plot the points on the graph and shade in the area of the triangle

More applications • Matrices can be used to change the position of points on a graph • The scalar multiplication factor can increase or decrease the overall size of the shape – resulting in greater or smaller area • This is called a dilation of the shape

Dilation of shapes • For the matrix, perform the scalar multiplication • Plot the original matrix and create the shape • Plot the dilated matrix (scalar multiplication answer) and create the new shape

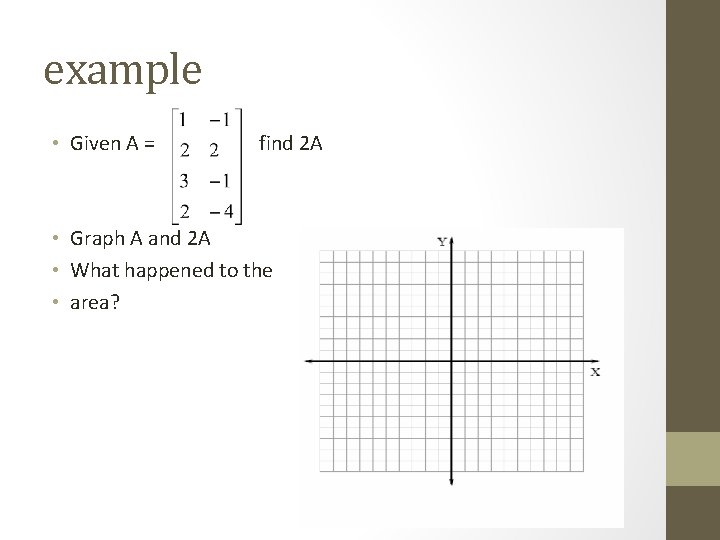
example • Given A = find 2 A • Graph A and 2 A • What happened to the • area?

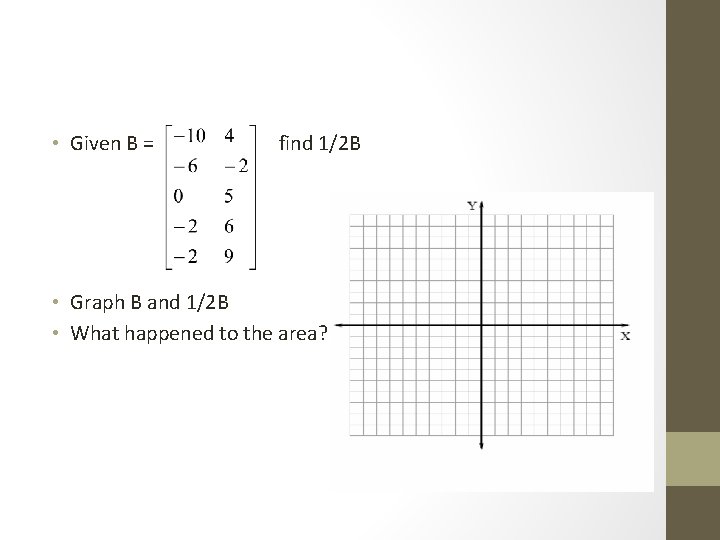
• Given B = find 1/2 B • Graph B and 1/2 B • What happened to the area?

Journal 7 • Why would using a matrix to increase or decrease the shape of an object be a useful tool to use?

Assignment: • Worksheet – • Perform the given operations for the scalar multiplication • Record on the worksheet • On graph paper • Plot the points from the original matrix – shade in the area in one color • Plot the points from the scalar matrix – shade in the area with a second color • Predict how the area has changed