VALUATION OF FIXED INCOME SECURITIES OR VALUATION OF

VALUATION OF FIXED INCOME SECURITIES OR VALUATION OF BONDS DR. U. HUSAIN

Structure Introduction Bond valuation Valuation model Bond return Price-yield relationship Bond market The term structure of interest rate (yield curve) Riding the yield curve Duration Immunization

Introduction Fixed income financial instruments: Traditionally identified as a long-term source of funds for a corporate enterprise are the cherished conduit for investor’s money. An assured return and high interest rate are responsible for the preference of bonds over equities.

Types of Bonds Financial institutions, banks and corporate bodies are offering attractive bonds like: Retirement bonds, Education bonds, Deep discount bonds, Encash bonds, Money multiplier bonds and index bonds.

Knowing how to value fixed income securities (bonds) is important both for investors and managers. (Such knowledge is helpful to the former in deciding whether Investor should buy or sell or hold securities at prices prevailing in the market. )

Bond Issuing Authorities A bond or debenture is a debt instrument issued by the: Government Public sectors Corporations (business enterprise)

Features of Bonds Type Typical Features Government- Guaranteed Bonds Medium- to long-term bonds issued by government agencies and guaranteed by the central government or a state government. Normally Coupon payments are semi-annual. PSU Bonds Medium- to long-term bonds issued by public sector companies in which the central or state government has an equity stake of 51 per cent or more. Corporate Bonds (Debentures) Short-to medium-term debt issued by private and public sector companies. Money Market Instruments Debt instruments like Treasury Bills (issued by Govt. ), Commercial Paper (issued by corporate) and Certificates of deposits (issued by banks and financial institutions) that have a maturity of less than a year.

valuation of bonds In order to understand the valuation of bonds, we need to be familiar with certain bond-related terms. Par Value- It is the value stated on the face of the bond. It represents the amount the firm borrows and promises to repay at the time of maturity. Usually the par or face value of bonds issued by business firms is $ 100. Sometimes it can be $ 1000.

Coupon Rate and Interest- A bond carries a specific interest rate which is called the coupon rate. The interest payable to the bond holder is simply par value of the bond x coupon rate. Most bonds pay interest semi-annually. For example, a GOI security which has a par value of $ 1000 and a coupon rate of 11 per cent pays an interest of $ 55 every six months.

Maturity Period- Typically, bonds have a maturity period of 1 -10 years; sometimes they have a longer maturity. At the time of maturity the par (face) value plus perhaps a nominal premium is payable to the bondholder.

Example: A company issues 1, 000, 10% Educational Bond @ $100 each. Par value; $ 100. Coupon Rate: 10% Maturity Value: $100

The time value concept of money is that the dollar received today is more valuable than a dollar received tomorrow. Future Value = present value (1 + interest rate). Example: If hundred dollars are put in a savings account in a bank for one year, the future value of money will be: Future Value = $ 100 (1. 0 + 6%) = 100 x 1. 06 = $ 106.

If the deposited money is allowed to cumulate for more than one time, the period exponent is added to the previous equation. Future value = (Present Value) (1 + interest rate)t n- the number of periods the deposited money accumulates as interest. Example: Suppose $ 100 is put for two years at the 6% rate of interest, money will grow to be $ 112. 36. Future Value = Present value (1 + interest rate)2 = 100 (1 + 0. 06) = 100 (1. 1236) = 112. 36. To find out the values in a simple manner, the compound sum of $1 at the end of a period FVIF 1, /r, t and compound sum of an annuity of $ 1 period FVIFA tables are given in the appendix.

The present value of money can be found simply by reversing the earlier equation. Present value x (1 + interest rate) = Future value Present value = Future value 1+ interest rate Here, the discounting principle is used. Today’s worth of $ 100 to be received after a year at 10 per cent interest would be: Present value = Future value 1+ interest rate = 100 = 100 1+ 0. 10 = $ 90. 90 1. 10 The multiple period of present value equation takes into account of the multiple periods. Future value____ Present value = (1 + interest rate)n

Bond Valuation model Determining the value of a bond requires: An estimate of expected cash flows An estimate of the required return. To simplify the analysis of bond valuation we will make the following assumptions: The coupon interest rate is fixed for the term of the bond. The coupon payments are made every year and the next coupon payment is receivable exactly a year from now. The bond will be redeemed at par on maturity.

The Formula for valuation of a bond is: P = C x PVIFA r X n + M x PVIF r X t Where, P = value (in dollar) n = number of years C = annual coupon payment (in dollar) r = periodic required return (i= Rate of Interest) M = maturity value t = time period when the payment is received.

Alternative Formula for Bond Valuation:

For Example: How to compute the value of a bond? Consider a 10 year, 12 % coupon bond with a par value of $ 1000. Let us assume that the required yield on this bond is 13%. The cash flows for this bond are as follows: 10 annual coupon payments of $ 120. $ 1000 principal repayment 10 years from now. The value of the bond is: P = 120 x PVIFA 13 X 10 + 1, 000 x PVIF 13 X 10 = 120 x 5. 426 + 1000 x 0. 295 = 651. 1 + 295 = $ 946. 1 Use Alternative Formula?

Bond values with semiannual interest Most bonds pay interest semi-annually. To value such bonds, we have to work with a unit period of six months, and not one year. This means that the bond valuation equation has to be modified along the following lines: The annual interest payment, C, must be divided by 2 to obtain the semi- annual interest payment. The number of years to maturity must be multiplied by two to get the number of half-yearly periods. The discount rate has to be divided by two to get the discount rate applicable to half-yearly period.

With the above modifications, the basic bond valuation becomes: P = C/2 (PVIFAr/2, 2 n) + M (PVIFr/2, 2 n) (10. 2) Where, P = value of the bond C/2 = semi-annual interest payment r/2 = discount rate applicable to a half-year period M = maturity value 2 n = maturity period expressed in terms of halfyearly periods. Same changes will come in Alternative Formula.

Example: Consider a 8 -year, 12 per cent coupon bond with a par value of $ 100 on which interest is payable semi-annually. The required return on this bond is 14 percent. Solution: P = C x PVIFA r X n + M x PVIF r X t = 6 (PVIFA 7%, 16 yr) + 100 (PVIF 7%, 16 yr) = $ 6 (9. 447) + $ 100 (0. 388) = $ 95. 5 Please use alternative formula?

Bond return Holding period return- An investor buys a bond and sells it after holding for a period. The rate of return in that holding period is: Price gain or loss during the holding period + Coupon interest rate, if any Holding period return = ______________ Price at the beginning of the holding period The holding period rate of return is also called the one period rate of return. This holding period return can be calculated daily or monthly or annually. If the fall in the bond price is greater than the coupon payment the holding period return will turn to be negative.

Example: (a) An investor ‘A’ purchased a bond at a price of $ 900 with $ 100 as coupon payment and sold it at $ 1000. What is holding period return ? Solution: Holding period return= Price gain + Coupon payment Purchase price 100 + 100 = 200 = 0. 2222 900 Holding period return = 22. 22%

(b) If the bond is sold for $ 750 after receiving $ 100 as coupon payment, then what is the holding period return? Holding period return= Price gain + Coupon payment Purchase price -150 + 100 = -50 = 0. 0555 900 Holding period return = -5. 55%

Current Yield The current yield is the coupon payment as a percentage of current market prices. Current yield = Annual coupon payment Current market price The current yield is the differs from the coupon rate, since the market price differs from the face value of the bond. When the bond’s face value and market price are same, the coupon rate and the current yield would be the same. For example, when the coupon payment is 8% for $ 100 bond with the same market price, the current yield is 8%. If the current market price is $ 80 then the current yield would be 10%.

Yield to maturity is the total return that will be earned by someone who purchases a bond and holds it until its maturity date. The yield to maturity might also be referred to as yield, internal rate of return, or the market interest rate at the time that the bond was purchased by the investor. The yield to maturity is expressed as an annual percentage rate. https: //www. accountingcoach. com/blog/what-is-yield-to-maturity

let's assume that a 5% $100, 000 bond will mature in 5 years and will pay interest each June 1 and December 1. Hence the bond will pay interest =100, 000 X(. 05)X(1/2) = $2, 500 every six months until it matures.

If the current market interest rate for this type of bond is 6%, the bond's current market value will be less than $100, 000. The market value of a 5% bond in a 6% bond market will be approximately $95, 735. This is the present value of the $2, 500 of interest that will be received every six months for 5 years plus the present value of the $100, 000 that will be received at the end of 5 years. Any difference in the re-investment rate will cause a difference between the actual return and the YTM. In this sense, the YTM is only a measure of yield. It cannot be regarded as a measure of return from a coupon-paying bond.

Example: A Ten-year bond with the 9% coupon rate and maturity value of $ 1000 is currently selling at $ 887. What is its yield to maturity?

Alternative Formula: YTM = C + (P or D/years to maturity) (PO + F) / 2 YTM= Yield to maturity C = Coupon interest P or D = Premium or discount PO = Present value F = Face value

Zero Coupon Bonds (ZCB) The YTM concept has a slightly different meaning for Zero Coupon Bonds (ZCB), popularly known as Deep Discount Bonds (DDB). ZCBs do not carry any coupon but Issued at a price discounted to the face value. On maturity, these bonds are redeemed at face value. Since these bonds do not have any coupon payments during the life of the bond, the question of reinvestment of coupon payments does not arise at all.

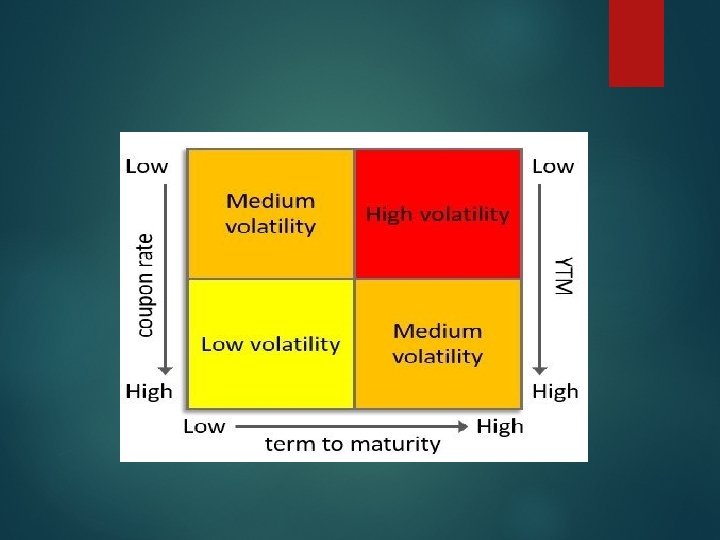
Price-yield relationship Bond prices and yields Price move in opposite directions, which you may find confusing if you're new to bond investing. Bond Prices and yields act like a Yield seesaw: when bond yield go up, prices go down, and when bond yields go down, prices go up.

Relationship between bond price and time Bond prices, generally, change with time as the price of a bond must equal its par value at maturity (assuming that there is no risk of default). For example, a bond that is redeemable for $1000 (which is its par value) after 5 years when it matures, will have a price of $ 1000 at maturity, no matter what the current price is?

Relationship between coupon rate, required yield, and price Coupon Rate < Required yield Price < Par (Discount bond) Coupon Rate = Required yield Price = Par Coupon Rate > Required yield Price > Par (Premium bond)

Realized yield to maturity Assumption: The YTM calculation assumes that the cash flows received through the life of a bond are reinvested at a rate equal to the yield to maturity. This assumption may not be valid as reinvestment rate/s applicable to future cash flows may be different. It is necessary to define the future reinvestment rates and figure out the realized yield to maturity.

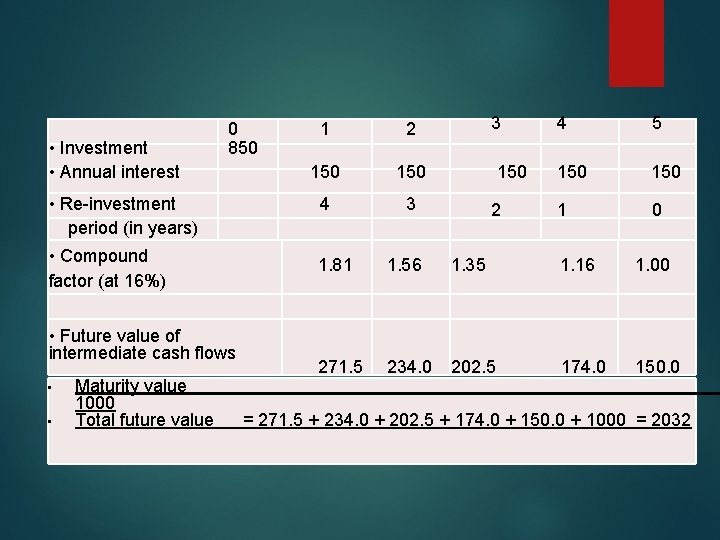
For Example: A $1000 par value bond, carrying an interest rate of 15 per cent (payable annually) and maturing after 5 years. The present market price of this bond is $ 850. The reinvestment rate applicable to the future cash flows of this bond is 16 per cent. The future value of the benefits receivable from this bond, calculated in bellow, works out to $ 2032.

• Investment • Annual interest • Re-investment period (in years) 0 850 1 4 • Compound factor (at 16%) 150 3 1. 81 3 2 2 1. 56 150 4 150 5 1 0 1. 35 1. 16 150 1. 00 • Future value of intermediate cash flows 271. 5 234. 0 202. 5 174. 0 150. 0 • Maturity value 1000 • Total future value = 271. 5 + 234. 0 + 202. 5 + 174. 0 + 150. 0 + 1000 = 2032

Bond market The bond market is a financial market where participants can issue new debt, known as the primary market, or buy and sell debt securities, known as the secondary market. This is usually in the form of bonds, but it may include notes, bills, and so on.

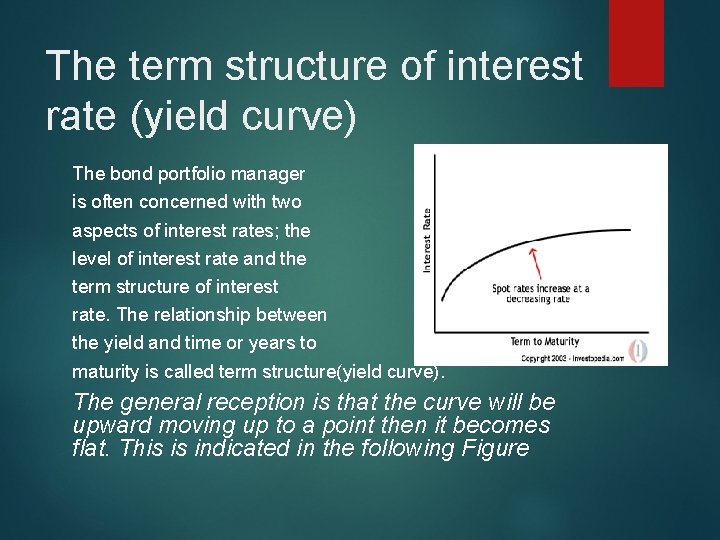
The term structure of interest rate (yield curve) The bond portfolio manager is often concerned with two aspects of interest rates; the level of interest rate and the term structure of interest rate. The relationship between the yield and time or years to maturity is called term structure(yield curve). The general reception is that the curve will be upward moving up to a point then it becomes flat. This is indicated in the following Figure

There at least three competing theories that attempt to explain the term structure of the interest rates. Expectation theory, Liquidity preference theory and Preferred habitat or segment theory

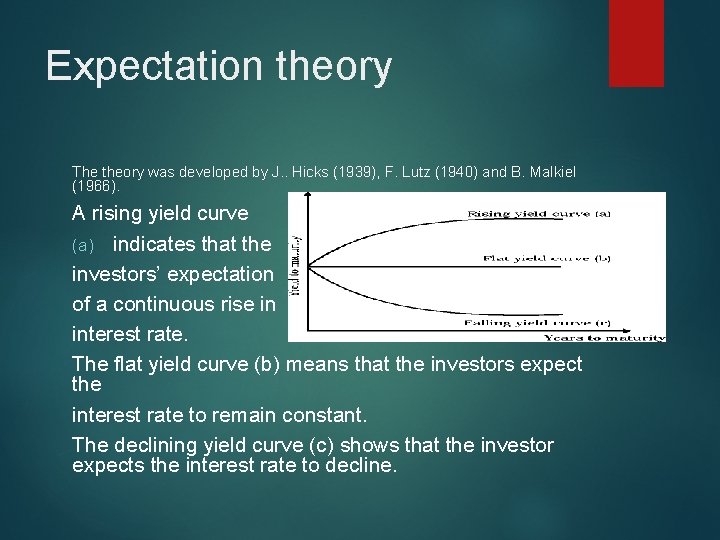
Expectation theory The theory was developed by J. . Hicks (1939), F. Lutz (1940) and B. Malkiel (1966). A rising yield curve (a) indicates that the investors’ expectation of a continuous rise in interest rate. The flat yield curve (b) means that the investors expect the interest rate to remain constant. The declining yield curve (c) shows that the investor expects the interest rate to decline.

Liquidity preference theory “Keynes describes the liquidity preference theory in terms of three motives that determine the demand for liquidity” (Tobin, J. 1958). The transactions motive: states that individuals have a preference for liquidity in order to guarantee having sufficient cash on hand for basic day-to-day needs. In other words, people have a high demand for liquidity to cover their short-term obligations, such as buying groceries, and paying rent or the mortgage. Higher costs of living mean a higher demand for cash/liquidity to meet those day-to-day needs. https: //www. investopedia. com/terms/l/liquiditypreference. asp

The precautionary motive: relates to individuals' preference for additional liquidity in the event that an unexpected problem or cost arises that requires a substantial outlay of cash. These include unforeseen costs like house or car repairs. The speculative motive: Individuals may also have a speculative motive. When interest rates are low, demand for cash is high as individuals prefer to use the cash or hold onto it until interest rates rise.

Keynes’ liquidity preference theory as advocated by J. R. Hicks (1939) Liquidity preference theory suggests that an investor demands a higher interest rate, or premium, on securities with long-term maturities, which carry greater risk, because all other factors being equal, investors prefer cash or other highly liquid holdings. Investments that are more liquid are easier to sell fast for full value. According to the liquidity preference theory, interest rates on short-term securities are lower because investors are not sacrificing liquidity for as long as they would be with medium- to longer-term securities.

Segmentation theory is stated that long and short-term interest rates are not related to each other. It also states that the prevailing interest rates for short, intermediate, and long-term bonds should be viewed separately like items in different markets for debt securities.

Riding the yield curve Riding the Yield Curve is a trading strategy that involves buying a long-term bond and selling it before it matures so as to profit from the declining yield that occurs over the life of a bond. Investors hope to achieve capital gains by employing this strategy.

The purchase of a security with a longer term to maturity t han the investor's expected holding period in order to produce increased returns by taking advantage of a positive yield c urve. For example, a $10, 000, 26 -week Treasury bill that yields 10% annually will sell for $9, 524, while a 13 week bill that yields 9% will sell for $9, 780. Buying the longer term security, holding it for 13 weeks, and selling it at the existing 13 week bill price will produce a profit of$256, for an annualized yie ld of ( $256/$9, 524 ) × 4, or 10. 75%. This yield is considerably higher

Duration is a measure of the sensitivity of the price of a bond or other debt instrument to a change in interest rate. Macaulay Duration: The Macaulay duration is the weighted average term to maturity of the cash flows from a bond. The weight of each cash flow is determined by dividing the present value of the cash flow by the price. Macaulay duration is frequently used by portfolio managers who use an immunization strategy.

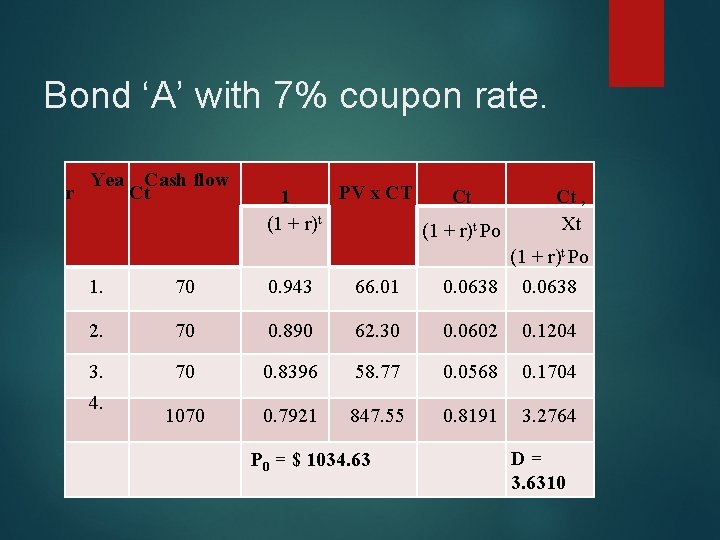
Example: Calculate the duration for bond A and Bond B with 7 per cent and 8 per cent coupons having maturity period of 4 years. The face value is $ 1000. Both the bonds are currently yielding 6 %.

Bond ‘A’ with 7% coupon rate. Yea Cash flow r Ct PV x CT 1 Ct (1 + r)t Po Ct , Xt 1. 70 0. 943 66. 01 (1 + r)t Po 0. 0638 2. 70 0. 890 62. 30 0. 0602 0. 1204 3. 70 0. 8396 58. 77 0. 0568 0. 1704 1070 0. 7921 847. 55 0. 8191 3. 2764 4. P 0 = $ 1034. 63 D = 3. 6310

Bond ‘B’ with 8% coupon rate. Year Cash flow Ct 1. 80 1 (1 + r)t PV x CT 0. 943 75. 44 0. 890 71. 200 Ct Ct , x t (1 + r)t Po 0. 0706 2. 3. 80 80 0. 8396 67. 168 0. 0666 0. 0628 4. 1080 0. 7921 855. 468 0. 8000 P 0 = $ 1069. 276 0. 1332 0. 1884 3. 2000 D = 3. 5922

From the above example, it is clear that the bond with larger coupon payments Example ‘A’ Bond ‘B’ Bond has a shorter duration compared to the bond with low coupon rate. Face value Coupon rate $ 1000. 00 7% $ 1000. 00 8% Years to maturity Macaulay’s duration 4. 0 3. 631 Years 4. 0 3. 592 Years

General rule Larger the coupon rate, lower the duration and less volatile the bond price. Longer the term to maturity, the longer the duration and more volatile the bond. Higher the yield to maturity, lower the bond duration and bond volatility, and vice versa. In a zero coupon bond, the bond’s term to maturity and duration are the same. The zero coupon bond makes only one time payment to repay the principal and interest on maturity.

Immunization

Investment outflow = (X 1 x Duration of bond 1) + (X 2, x Duration of bonds 2) + and so on… X 1, X 2 proportion of investment on bond 1 and 2.

Exapmle: Ali has $ 50, 000 to make one time investment. His son has entered the Higher Secondary school and he needs his money back after two years for his son’s educational expenses. As Ali’s outflow is one time outflow, duration is simply two years. Now he has a choice of two types of bonds. Bond ‘A’ has a coupon rate of 7 per cent and maturity period of four years with a current yield of 10 per cent. Current price is $ 904. 90. Bond ‘B’ has the coupon rate of 6 per cent, a maturity period of one year and a current yield of 10 per cent. The current price is $ 963. 64.

Risk The two bonds pose two types of risk to him. He can invest all his money in bond ‘B’ with the aim of reinvesting the proceeds from the maturing bonds into another issue of one year period. If the interest rate declines in the market during the next year, he has to reinvest his money in low yielding bonds and may incur a loss. Now, he has to face the reinvestment risk.

On the other hand, if he invests his money in ‘A’ bond, that also involves certain amount of risk. He cannot hold it till it matures, because he needs the money after two years and has to sell it in the middle. If there is a rise in the market interest rate then the price of the bond will fall down and vice versa. If a rise in interest rate is assumed, the investor has to incur loss.

Solution. Ali can solve the problem by investing part of the money in one year bonds and a part in four year bonds. But, he should know how much to be invested in each of these bonds. This can be got by solving the following equation. (X 1 x D 1) + (X 2 x D 2) = 2

X 1 = the proportion of investment in bond ‘A’ X 2 = the proportion of investment in bond ‘B’ D 1 = Duration of bond ‘A’ D 2 = Duration of bond ‘B’

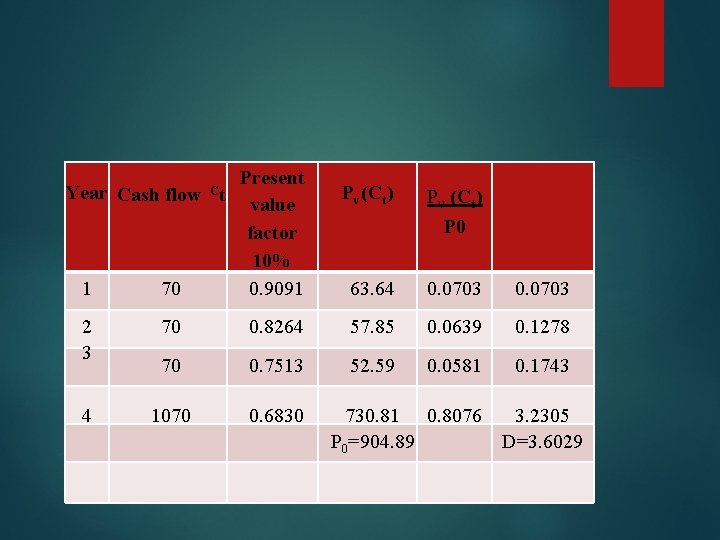
1 70 Present value factor 10% 0. 9091 2 3 70 0. 8264 57. 85 0. 0639 0. 1278 70 0. 7513 52. 59 0. 0581 0. 1743 4 1070 0. 6830 Pv(Ct) PV (Ct) P 0 63. 64 0. 0703 730. 81 0. 8076 P 0=904. 89 Year Cash flow Ct 3. 2305 D=3. 6029

Applying the formula: (X x 1) + (X 2 x 3. 6030) = 2 X: can be written as (1 - X 2), then [(1 - X 2)1] + [X 2. 3. 603] = 2 1 - X 2 + 3. 6030 X 2 = 2 X 2 = 0. 3842 X 1 = 0. 6158 Ali should put 61. 58% of his investible funds in one year bond and 38. 42 per cent in the four year bond.

Key Words Par Value is the value stated on the face of the bond. Coupon Rate and Interest bond carries a specific interest rate which is called the coupon rate. Time value concept of money is that the dollar received today is more valuable than a dollar received tomorrow. Holding period return is a return on a bond after holding it for a period. YTM Yield to Maturity is the rate of return, which an investor can expect to earn if the bond is held till maturity. ZCBs Zero Coupon Bonds do not carry any coupon rate but are issued at a price discounted to the face value. Current yield is the coupon payment as a percentage of current market prices. Term Structure is relationship between the yield and time or years to maturity and is also known as yield curve. Expectation theory according to the this theory, the shape of the yield curve can be explained by the expectations of the investors about the future interest rates. Liquidity preference theory advocates that expectations influence the shape of the yield curve. Duration measures the time structure of a bond and the bond’s interest rate risk.

Sample Questions: How would you assess the present value of a bond? Explain the various bond value theories with examples. Discuss the term structure of the interest rate? How do theories explain the term structure of the interest rate? What is meant by duration? Explain the relationship between duration and price change. How would you immunize the bond portfolio using the immunization technique?

Problems 1) The bonds of the Nordy Company have a coupon interest rate of 9%. The interest on the bonds is paid semiannually, the bonds mature in 8 years, and their par value is $1, 000. If the required rate of return 8%, what is the value of each bond? What is the value of each bond if the interest is paid annually? 2) You own a bond that pays $100 in interest annually, has a par value of $1000, and matures in 15 years. What is the value of the bond if your required rate of return is 12%? What is the value of the bond if your required rate of return (a) increases to 15% or (b) decreases to 8%? Now, recompute all three answers assuming that the bond matures in 5 years instead of 15 years. 3) Dullco Company bonds are selling in the market for $1, 045 (104. 50). These bonds will mature in 15 years and pay $70 in interest annually. If the bonds are purchased at the market price, what is the (a) coupon rate, (b) current yield, (c) approximate yield to maturity and (d) capital gains yield? 4) Apex Company is planning to issue zero coupon bonds that will mature at $1, 000 in 20 years. If your required rate of return on these bonds is 9. 35%, what are you willing to pay for the bonds? If these bonds are currently selling for $213. 50, what is their yield to maturity (YTM)? 5) Find out the yield to maturity on a 8 per cent 5 year bond selling at $ 105?

6). (a) Determine the present value of the bond with a face value of $ 1000, coupon rate of $ 90, a maturity period of 10 years for the expected yield to maturity of 8 per cent. (b) If N is equal to 7 years in the above example, determine the present value of the bond. Discuss the effect of the maturity period on the value of the bond. 7). Bond A and B have similar characters except the maturity period. Both the bonds carry 9 per cent coupon rate with the face value of $ 10, 000. The yield to maturity is 9%. If the yield to maturity is to rise to 11% what will be the respective percentage price change in bond A with 7 years to maturity and B with 10 years to maturity? 8). A bond with the face value of $ 1000 pays a coupon rate of 9 per cent. The maturity period is 9 years (a) Find out the approximate yield to maturity (b) current yield and the nominal interest rate. 9). Determine the yield to maturity if a zero coupon bond with a face value of $ 1000 is sold at $ 300. The maturity period is 10 years 10) Mr. Sultan is considering the purchase of a bond currently selling at $ 878. 50 the bond has four years to maturity, face value of $ 1, 000 and 8% coupon rate. The next annual interest payment is due after one year from today. The required rate of return is 10%. Calculate the intrinsic value (Present value) of the bond. Should Mr. Sultan buy the bond? Calculate the yield to maturity of the bond. 11). What is the value of a $ 1, 000 bond that paying 5 per cent annual coupon rate in semiannual payments over 5 years until it mature if its yield to maturity is 7 per

Tobin, J. (1958). Liquidity preference as behavior towards risk. The review of economic studies, 25(2), 65 -86. Hicks, J. R. 1939. Value and capital, Oxford: Oxford University Press. [Google Scholar] https: //www. accountingcoach. com/blog/what-is-yield-to -maturity Hicks, J. R. (1936). Keynes' theory of employment. The Economic Journal, 46(182), 238 -253.

THANKS DR. U. Husain