Valley Math Series Session 2 Rich Math Tasks

Valley Math Series Session #2 Rich Math Tasks S

Today we will. . . 1. Revisit & Extend Our Thinking about Number Talks 2. Develop a common understanding of what makes a rich task. 3. Deepen our thinking about the structure of a task-based lesson.

Session 1 Follow-Up: Number Talks What did you try? How did it go? What did you notice about student thinking?

Focus Question How can we decide which Talk Move will most enhance the math discourse?

32 x 15

Another Number Routine: Today’s Number 16

st 1 Grade

From nd 2 Grade Olivia’s example: The answer is _____ what might the problem be?

Rich Mathematical Tasks: Pentomino Investigation Table Talk: What are important characteristics of a rich math task? S

Research-Based Criteria for Rich Math Tasks Is it mathematically interesting? Does it invite constructive struggle and perseverance? Is there more than one path to a solution? Does it allow for different levels of learning? Does it leave behind mathematical residue? Is the need for communication embedded in the task? Is it embedded in a problem solving context?

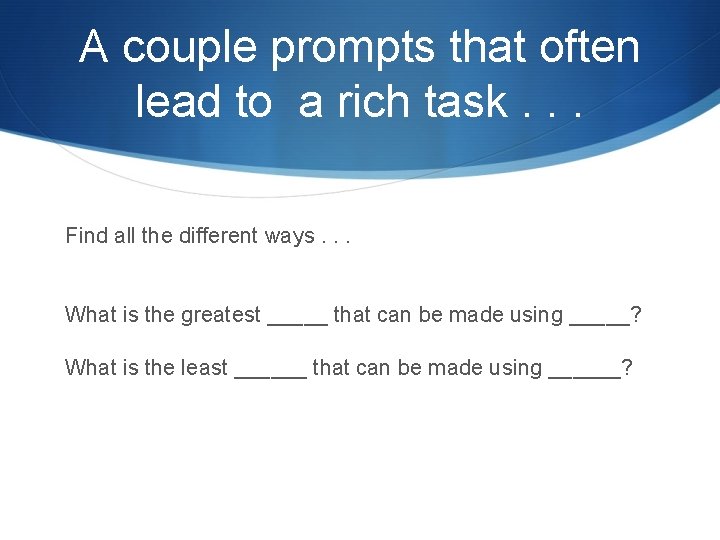
A couple prompts that often lead to a rich task. . . Find all the different ways. . . What is the greatest _____ that can be made using _____? What is the least ______ that can be made using ______?

Common Core Content and Practice Standards in this Exploration… Content Focus: Measurement Practice Standards Foregrounded: #3 -Construct viable arguments and critique the reasoning of others #7 -Look for and make use of structure

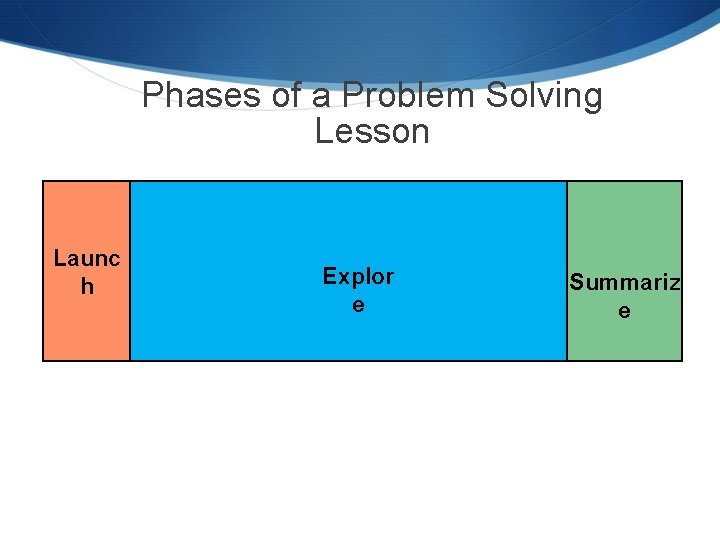
Phases of a Problem Solving Lesson Launc h Explor e Summariz e

Materials Color tiles 1 inch squared paper Scissors Tape or Glue Stick Markers

LAUNCH: Rules for Arranging our Tiles and Naming our Shapes Omino Domino Not Dominoes

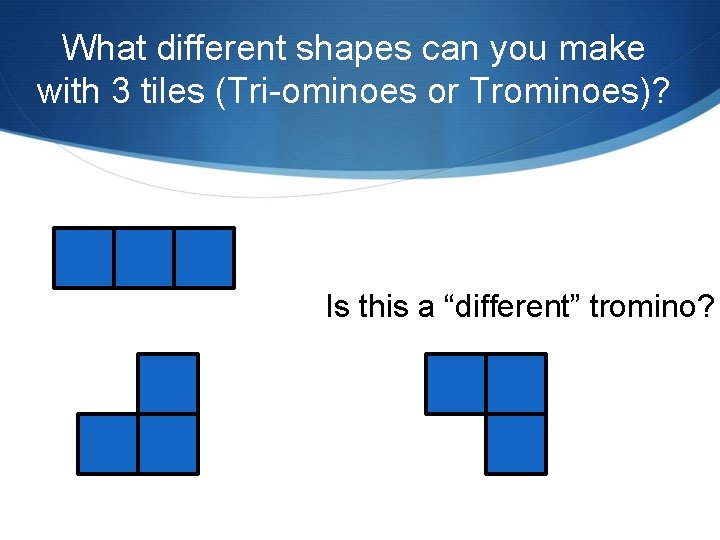
What different shapes can you make with 3 tiles (Tri-ominoes or Trominoes)? Is this a “different” tromino?

Find all the different arrangements using four tiles.

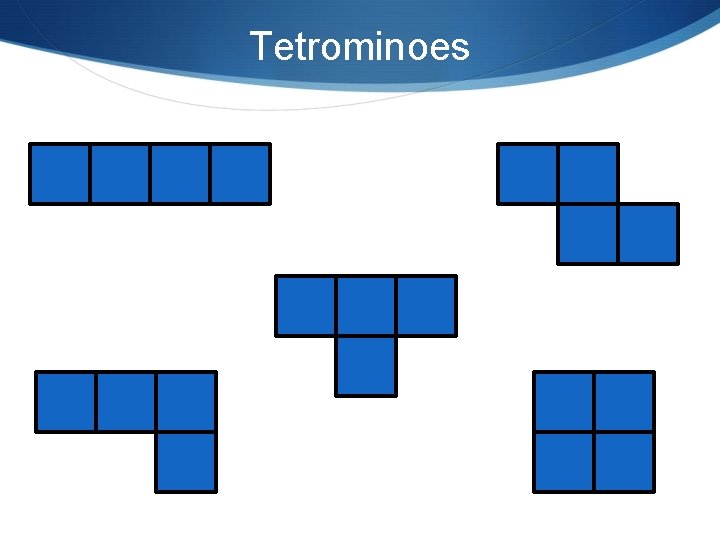
Tetrominoes

Predicting Pentominoes How many different arrangements do you predict you can make with five tiles?

EXPLORE: Pentomino Task TASK 1: 1. Find all the pentomino arrangements that you can using 5 color tiles. 2. Cut the pentomino arrangements from 1 inch grid paper. 3. Each pair needs only 1 set of cutout pentomino arrangements. 4. When you decide you have found all the possible pentomino arrangements, discuss with each other how you know for sure that you have found them all. 5. Write a statement that explains how you know you have them all. TASK 2: Label each pentomino with its area and perimeter. What do you notice?

SUMMARIZE: Summarizing the Exploration as a Math Learner TASK 1: How many different pentominoes did you find? How do you know you found all the different pentominoes? What system did you use when you were finding all the ways? TASK 2: What did you notice about the area and perimeters?

Summarizing the Experience as a Teacher Ø How were you engaged in math practices 3 & 7? 3: Construct viable arguments and critique the reasoning of others. 7: Look for and make use of structure. Ø Which elements of rich math tasks caught your attention as you engaged in the pentomino exploration? Why? Ø What instructional moves and decisions positively contributed to your learning during this task?

Analyzing Tasks for Your Grade Level Pentomino Extensions Yarn Shapes Fish combinations S Which task makes the most sense for your students? S How will you structure the lesson?

Reflections and Goal Setting Please discuss with a partner, then complete the reflection form and leave it face down on your table. What important ideas will you take away from today’s session? What strategy or activity will you try in your classroom and be prepared to share at the next Wednesday workshop? Anything else? Next Workshop: Sept. 20, Procedural Fluency

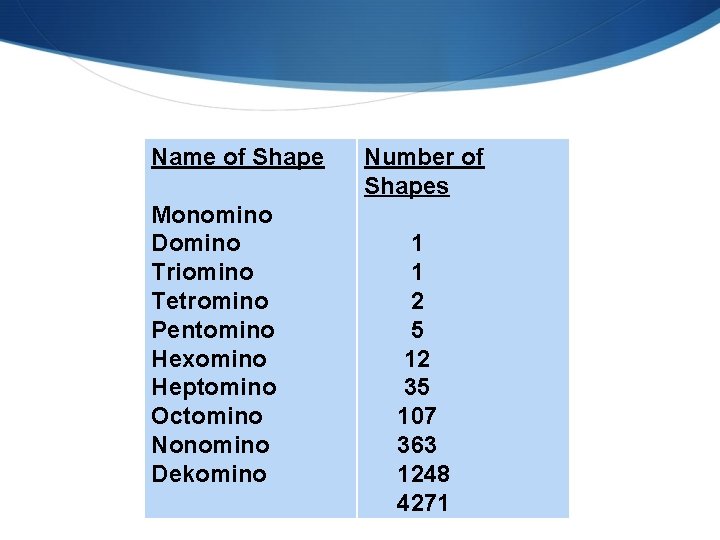
Did you find all the pentominoes?

Pentomino Name of Shape Number of Hexomino Shapes Monomino Heptomino 1 Domino Triomino 1 Octomino Tetromino 2 Pentomino Nonomino 5 Hexomino 12 Dekomino 35 Heptomino Octomino Nonomino Dekomino 107 363 1248 4271

Sources for Rich Tasks S Robert Kaplinsky: http: //robertkaplinsky. com/ S Nrich: https: //nrich. maths. org/ S VES Math