Validation of the PWA for BES PWA working

Validation of the PWA (for BES PWA working group) YANPING HUANG Institute of High Energy Physics, Bei. Jing 2009 -5 -26

Outline n Motivation n PWA fit methods tested Ø Ø Ø n Event-by-event fit Bin-by-bin fit Binned phase space input fit Binned ML fit GPU Summary

Motivation n PWA is a key technique in hadron spectroscopy studies Spin-parity determination Interference among different processes n n PWA is complicated Are PWA results reliable, especially with many parameters in the fit? It is necessary to do MC input/output checks to validate PWA methods.

Input/Output checks : n n Parameters of each resonance (mass, width and event number (fraction)) : consistency of the parameters value within errors Sensitivity check: Fit error of the parameter is obtained from a single sample, it can represent sensitivity directly. RMS of the parameter is obtained from many samples, it can represent truth statistical errors. It can be performed in MC study. If the fit error is correct, it should be similar to the RMS. In such case, the sensitivity can be estimated correctly.

Input/Output check : Statistic Significance Check (hypothesis test) n n estimated parameters: mass, width, amplitude, phase angle Hypothesis H 0 : i resonances -> ni parameters with gauss distribution，likelihood value is L 0: Hypothesis H 1 : i+1 resonances -> ni+Dn parameters with gauss distribution, likelihood value is L 1: Ds should obey c 2 distribution with Dd. o. f = Dn.

Standard PWA procedure at BESII The probability density function: ξ: momentum combination of final state; σ: calculated by Covariant Tensor formalism (Eur. Phys. J. A 16, 537 -547, 2003) Likelihood function: Event-by-event fit

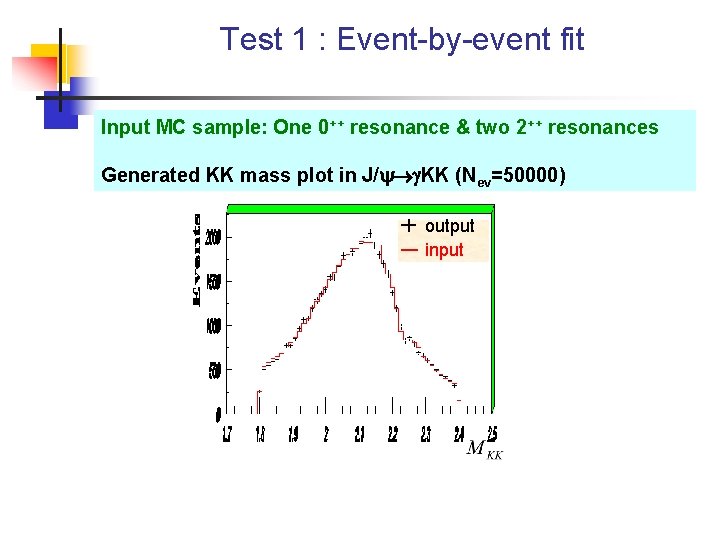
Test 1 : Event-by-event fit Input MC sample: One 0++ resonance & two 2++ resonances Generated KK mass plot in J/ KK (Nev=50000) output input

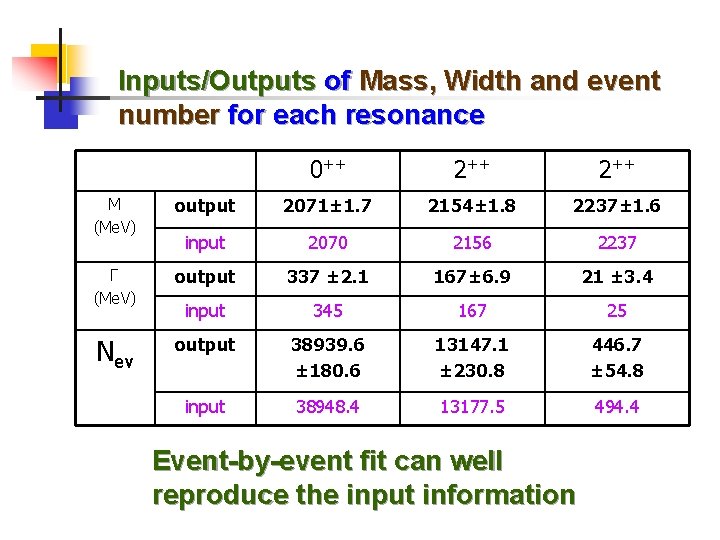
Inputs/Outputs of Mass, Width and event number for each resonance 0++ 2++ M (Me. V) output 2071± 1. 7 2154± 1. 8 2237± 1. 6 input 2070 2156 2237 Γ (Me. V) output 337 ± 2. 1 167± 6. 9 21 ± 3. 4 input 345 167 25 Nev output 38939. 6 ± 180. 6 13147. 1 ± 230. 8 446. 7 ± 54. 8 input 38948. 4 13177. 5 494. 4 Event-by-event fit can well reproduce the input information

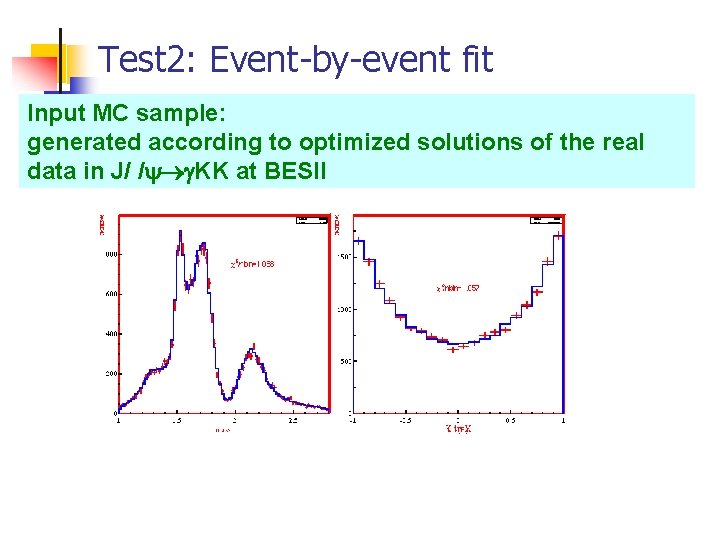
Test 2: Event-by-event fit Input MC sample: generated according to optimized solutions of the real data in J/ / KK at BESII

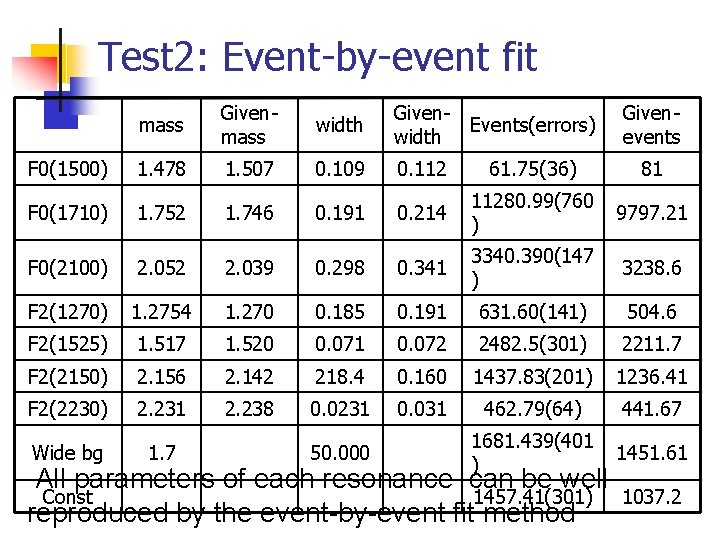
Test 2: Event-by-event fit mass Givenmass width Given. Events(errors) width F 0(1500) 1. 478 1. 507 0. 109 0. 112 61. 75(36) 81 F 0(1710) 1. 752 1. 746 0. 191 0. 214 11280. 99(760 ) 9797. 21 F 0(2100) 2. 052 2. 039 0. 298 0. 341 3340. 390(147 ) 3238. 6 F 2(1270) 1. 2754 1. 270 0. 185 0. 191 631. 60(141) 504. 6 F 2(1525) 1. 517 1. 520 0. 071 0. 072 2482. 5(301) 2211. 7 F 2(2150) 2. 156 2. 142 218. 4 0. 160 1437. 83(201) 1236. 41 F 2(2230) 2. 231 2. 238 0. 0231 0. 031 462. 79(64) 441. 67 Wide bg 1. 7 1681. 439(401 ) 1451. 61 50. 000 All parameters of each resonance can be well Const 1457. 41(301) reproduced by the event-by-event fit method Givenevents 1037. 2

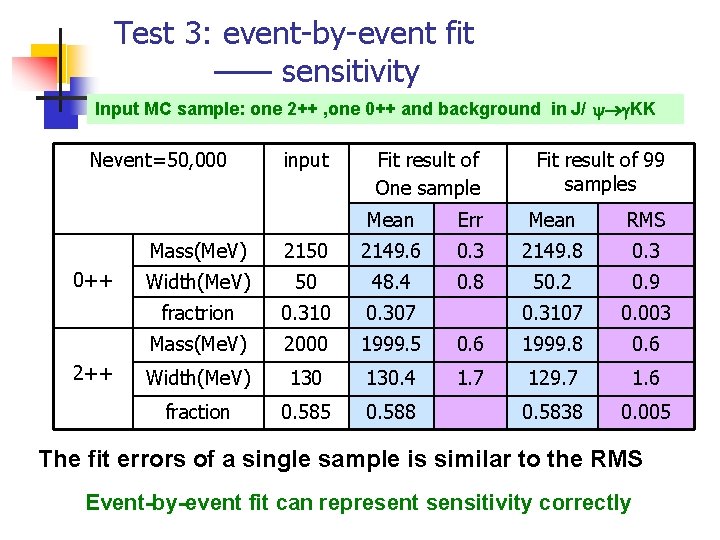
Test 3: event-by-event fit —— sensitivity Input MC sample: one 2++ , one 0++ and background in J/ KK Nevent=50, 000 0++ 2++ input Fit result of One sample Fit result of 99 samples Mean Err Mean RMS Mass(Me. V) 2150 2149. 6 0. 3 2149. 8 0. 3 Width(Me. V) 50 48. 4 0. 8 50. 2 0. 9 fractrion 0. 310 0. 307 0. 3107 0. 003 Mass(Me. V) 2000 1999. 5 0. 6 1999. 8 0. 6 Width(Me. V) 130. 4 1. 7 129. 7 1. 6 fraction 0. 585 0. 588 0. 5838 0. 005 The fit errors of a single sample is similar to the RMS Event-by-event fit can represent sensitivity correctly

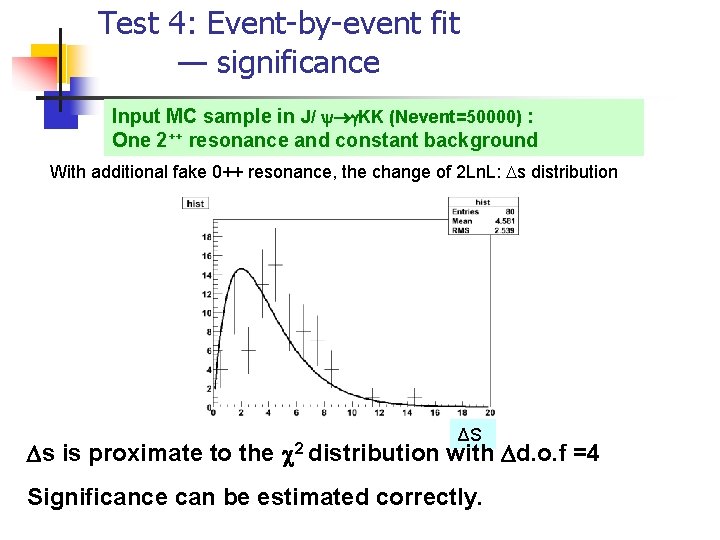
Test 4: Event-by-event fit — significance Input MC sample in J/ KK (Nevent=50000) : One 2++ resonance and constant background With additional fake 0++ resonance, the change of 2 Ln. L: Ds distribution Ds is proximate to the c 2 distribution ΔS with Dd. o. f =4 Significance can be estimated correctly.

n n n We perform extensive checks on the event-byevent fit method, including MC input samples containing 7 resonances as in the real data of J/ K+K-process. All tests show that the output can well reproduce the input. All the published PWA results at BESII are based on the event-by-event PWA method.

PWA procedure of Bin-by-bin fit Ø Divide the mass spectrum into many (~100) bins. Ø In each bin, we only fit various JPC components without BW structure. Ø We can perform PWA fits for all bins on many parallel CPUs. Ø Get the mass, width and event number of each resonances by fitting mass spectrum of each component

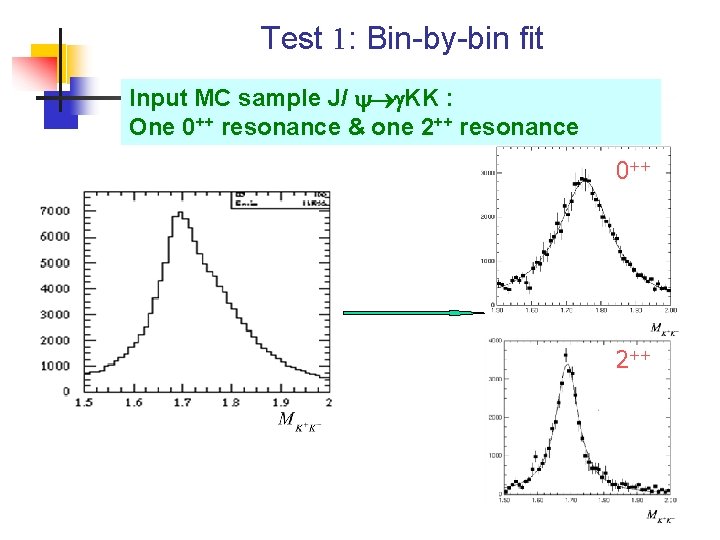
Test 1: Bin-by-bin fit Input MC sample J/ KK : One 0++ resonance & one 2++ resonance 0++ 2++

Inputs/Outputs of Mass, Width and event number for each resonance 0++ 2++ Output Input Fit Input Nev 63874± 814 65567 39322± 814 38099 M(Me. V) 1753. 3± 1. 6 1750 1690. 1± 1. 1 1690 200 83. 4± 2. 8 Γ(Me. V) 186. 5± 3. 9 80 It seems bin-by-bin fit can reproduce the input information.

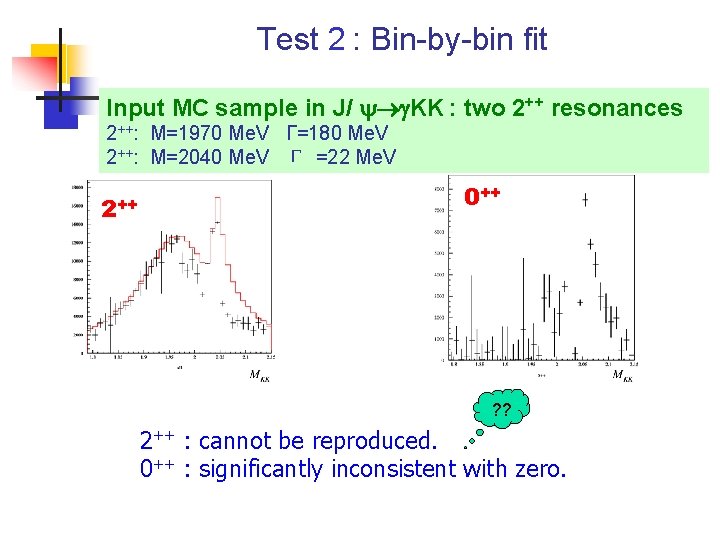
Test 2 : Bin-by-bin fit Input MC sample in J/ KK : two 2++ resonances 2++: M=1970 Me. V Г=180 Me. V 2++: M=2040 Me. V Г =22 Me. V 2++ 0++ ? ? 2++ : cannot be reproduced. 0++ : significantly inconsistent with zero.

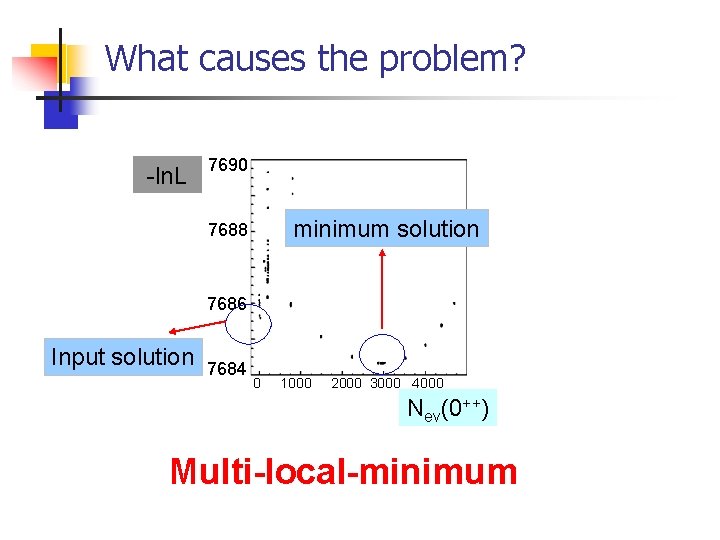
What causes the problem? -ln. L 7690 minimum solution 7688 7686 Input solution 7684 0 1000 2000 3000 4000 Nev(0++) Multi-local-minimum

Check in the event-by-event fit 2++ Event-by-event fit : well reproduce the inputs. n Event-by-event fit results are more reliable than bin-by-bin fit.

PWA procedure of Binned PS input fit n n n φ0 : azimuth angle of K- in J/ cosθ 0 : cosine of polar angle of K- in J/ cosθ 1 : cosine of polar angle of K+ in K+ φ1 : azimuth angle of K+ in K+ M K+ : invariant mass of K+ New Inputs of PWA: 4 momentum in each bin and number of events in each bin The PWA speed depends on number of bins.

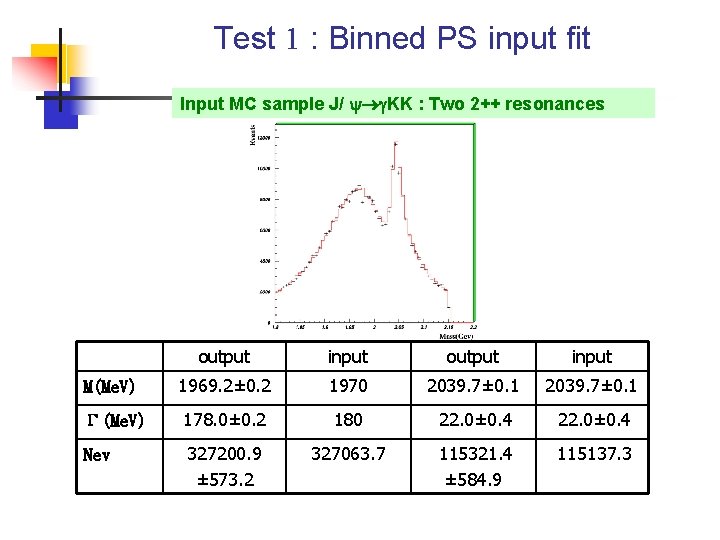
Test 1 : Binned PS input fit Input MC sample J/ KK : Two 2++ resonances output input M(Me. V) 1969. 2± 0. 2 1970 2039. 7± 0. 1 Γ(Me. V) 178. 0± 0. 2 180 22. 0± 0. 4 Nev 327200. 9 ± 573. 2 327063. 7 115321. 4 ± 584. 9 115137. 3

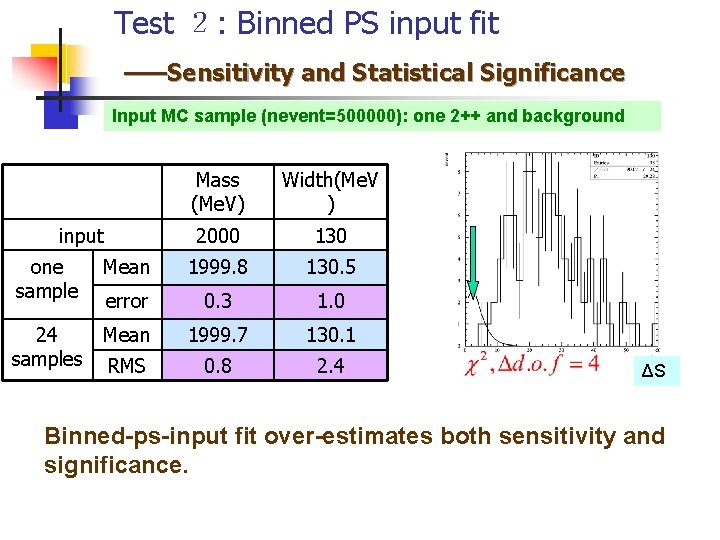
Test ２: Binned PS input fit ——Sensitivity and Statistical Significance Input MC sample (nevent=500000): one 2++ and background input Mass (Me. V) Width(Me. V ) 2000 130 one sample Mean 1999. 8 130. 5 error 0. 3 1. 0 24 samples Mean 1999. 7 130. 1 RMS 0. 8 2. 4 ΔS Binned-ps-input fit over-estimates both sensitivity and significance.

PWA procedure of Binned ML fit n cosθ 0 : cosine of polar angle of in J/ cosθ 1 : cosine of polar angle of K+ in k-K+ φ1 : azimuth angle of K+ in k-K+ n M n n n k+K- : invariant mass of k+K- According to the rigorous deduction of the likelihood in statistic（see Liubj’s talk）: New Inputs of PWA: Observed event number (nb) for real data and FUNij for the mc sample in each bin The PWA speed depends on number of bins.

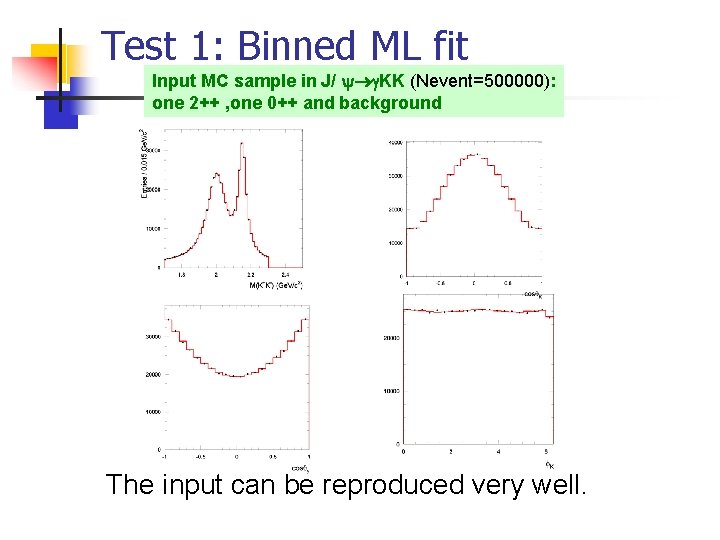
Test 1: Binned ML fit Input MC sample in J/ KK (Nevent=500000): one 2++ , one 0++ and background The input can be reproduced very well.

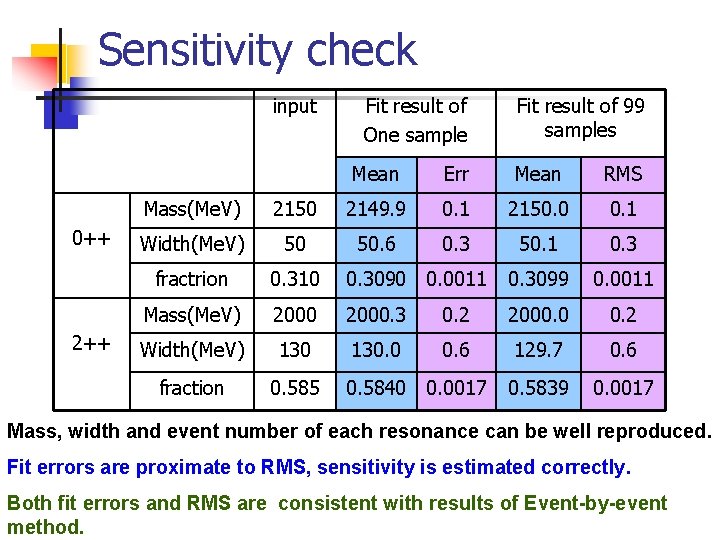
Sensitivity check input 0++ 2++ Fit result of One sample Fit result of 99 samples Mean Err Mean RMS Mass(Me. V) 2150 2149. 9 0. 1 2150. 0 0. 1 Width(Me. V) 50 50. 6 0. 3 50. 1 0. 3 fractrion 0. 310 0. 3090 0. 0011 0. 3099 0. 0011 Mass(Me. V) 2000. 3 0. 2 2000. 0 0. 2 Width(Me. V) 130. 0 0. 6 129. 7 0. 6 fraction 0. 585 0. 5839 0. 0017 0. 5840 0. 0017 Mass, width and event number of each resonance can be well reproduced. Fit errors are proximate to RMS, sensitivity is estimated correctly. Both fit errors and RMS are consistent with results of Event-by-event method.

Significance check With additional fake 0++ resonance, the change of 2 Ln. L: Ds distribution n It can provide correct fitting results, mean value, error, sensitivity, significance, etc

How to divide bins n n Experiment technology before PWA: project distribution, such as the invariant mass spectrum, angle distribution. PWA at BESII: make use of momentum of final state particles as the input information to determine events, for J/ -> k+k-，there are 9 variables. Considering the energy-momentum constraint, there are 5 freedom degrees. n f 0 : azimuth angle of in J/ (contribution should be uniform) cosθ 0: cosine of polar angle of in J/ cosθ 1: cosine of polar angle of K+ in k-K+ φ1 : azimuth angle of K+ in k-K+ n Mk+K- : invariant mass of k+K- n n n

How to divide bins n n bin size: more bins, more information kept, but lower speed balance Dimension: number of variables the sensitivity of the variable

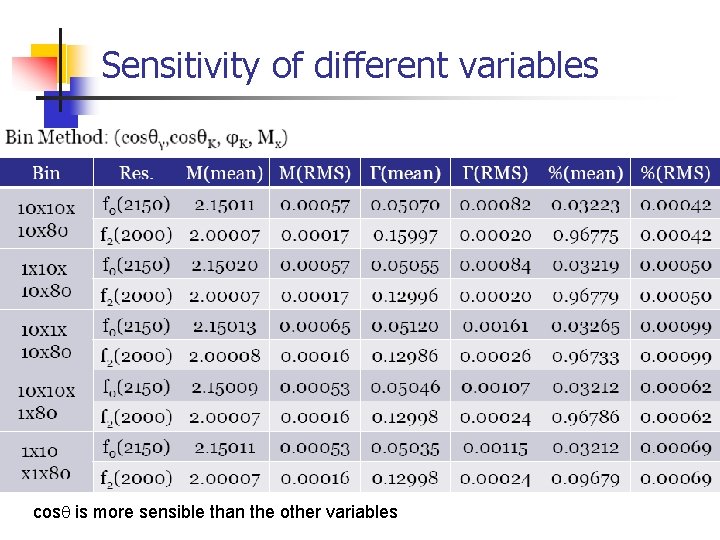
Sensitivity of different variables cosq is more sensible than the other variables

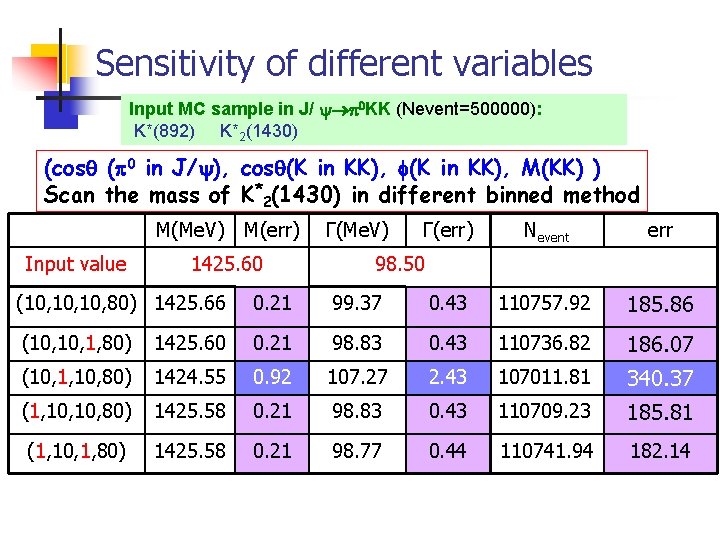
Sensitivity of different variables Input MC sample in J/ 0 KK (Nevent=500000): K*(892) K*2(1430) (cos ( 0 in J/ ), cos (K in KK), M(KK) ) Scan the mass of K*2(1430) in different binned method M(Me. V) Input value M(err) 1425. 60 Γ(Me. V) Γ(err) Nevent err 98. 50 (10, 10, 80) 1425. 66 0. 21 99. 37 0. 43 110757. 92 185. 86 (10, 1, 80) 1425. 60 0. 21 98. 83 0. 43 110736. 82 186. 07 (10, 1, 10, 80) 1424. 55 0. 92 107. 27 2. 43 107011. 81 340. 37 (1, 10, 80) 1425. 58 0. 21 98. 83 0. 43 110709. 23 185. 81 (1, 10, 1, 80) 1425. 58 0. 21 98. 77 0. 44 110741. 94 182. 14

Test of GPUPWA

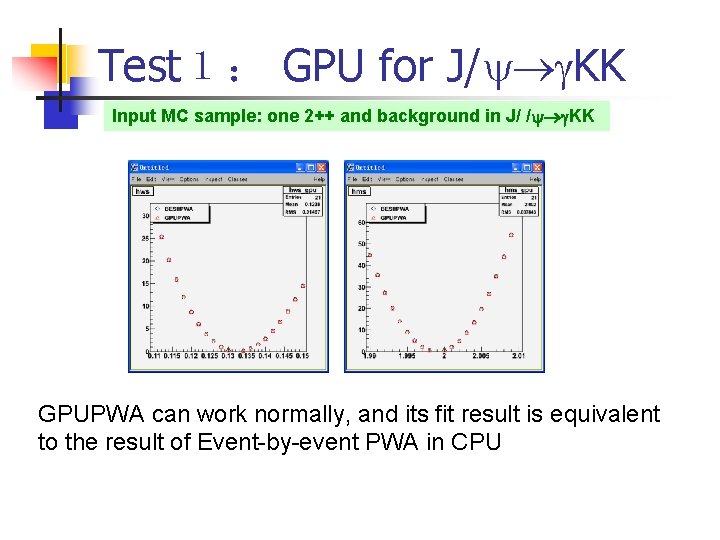
Test１： GPU for J/ KK 　 Input MC sample: one 2++ and background in J/ / KK GPUPWA can work normally, and its fit result is equivalent to the result of Event-by-event PWA in CPU

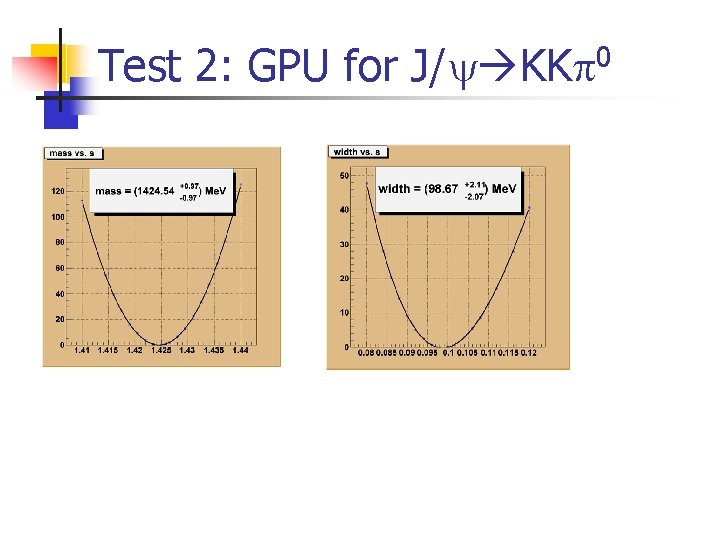
Test 2: GPU for 0 J/ KK

Compare the PWA fit methods n Event-by-event fit: provide reliable solution, but the speed becomes very slow for huge sample. n Bin-by-bin fit: there exist multi-local-minimum. n Binned-PS-input fit: the sensitivity and significance is over-estimated. n Binned ML fit: can provide robust solution with high speed. n GPU : perform the PWA of J/ KK and J/ 0 KK successfully, also provide robust solution with high speed.

Summary n n n Different PWA fit methods have been tested. Binned ML fit Method and GPUPWA can obtain PWA robust results with high speed. The combination of binned ML fit and GPU technology is under working. More tests will be performed. —— You are welcome to join us!

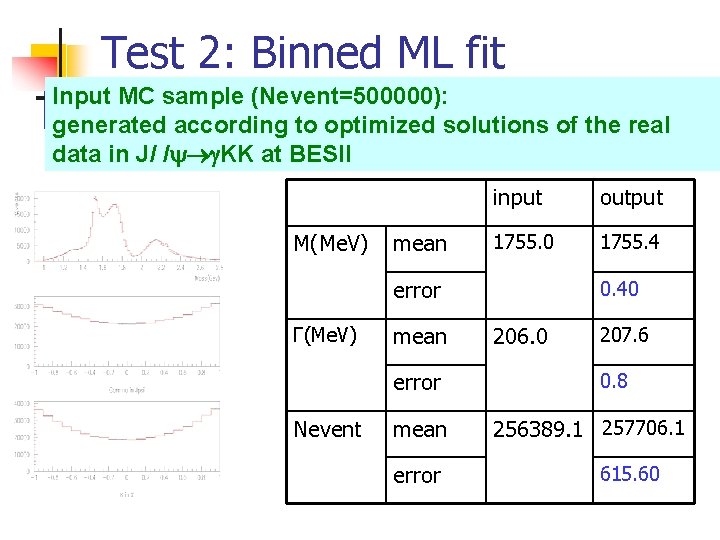
Test 2: Binned ML fit Input MC sample (Nevent=500000): generated according to optimized solutions of the real data in J/ / KK at BESII M(Me. V) mean input output 1755. 0 1755. 4 error Γ(Me. V) mean error Nevent mean error 0. 40 206. 0 207. 6 0. 8 256389. 1 257706. 1 615. 60