Valid and Invalid Arguments M 260 2 3

Valid and Invalid Arguments M 260 2. 3

Argument • An argument is a sequence of statements. The final statement is called the conclusion, the others are called the premises. • = “therefore” before the conclusion.

Logical Form • If Socrates is a human being, then Socrates is mortal; Socrates is a human being; Socrates is mortal. • If p then q; p; q

Valid Argument • An argument form is valid means no matter what particular statements are substituted for the statement variables, if the resulting premises are all true, then the conclusion is also true. • An argument is valid if its form is valid.

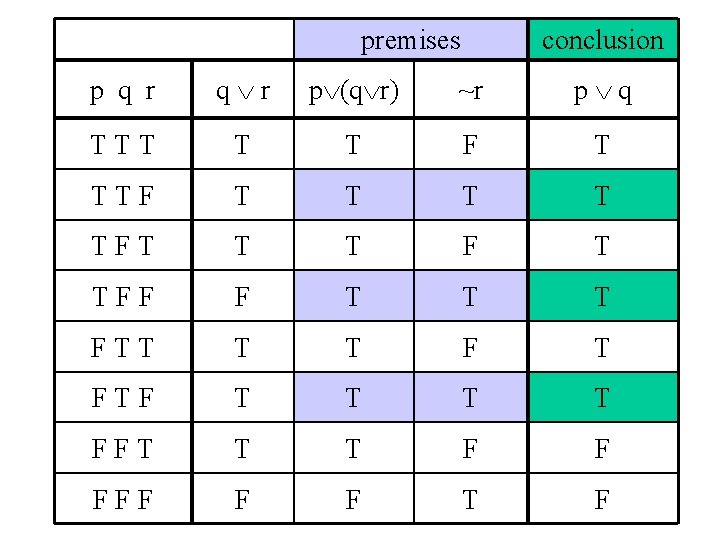
Test for Validity • Identify premises and conclusion • Construct a truth table including all premises and conclusion • Find rows with premises true (critical rows) • If conclusion is true on all critical rows, argument is valid • Otherwise argument is invalid

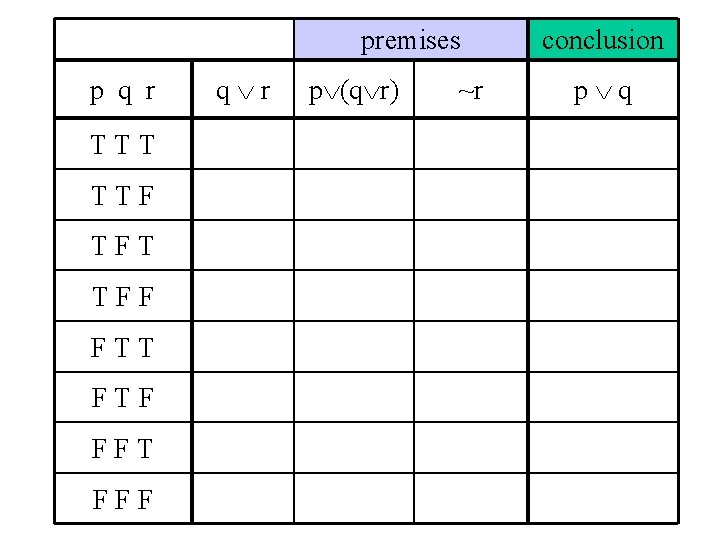
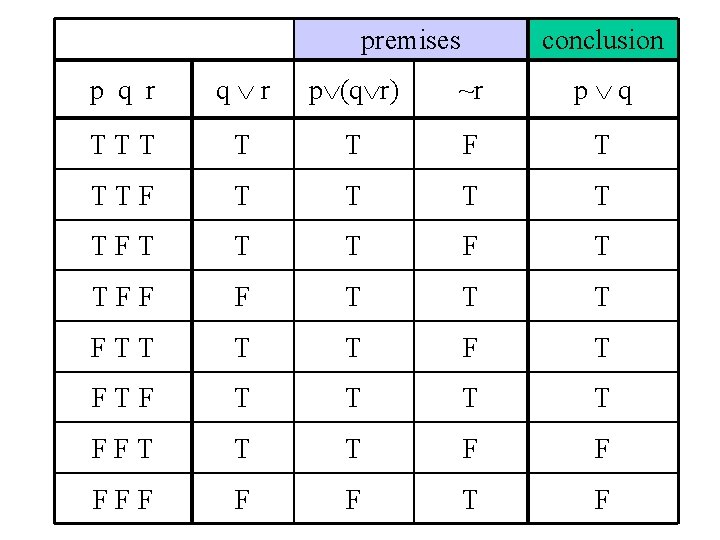
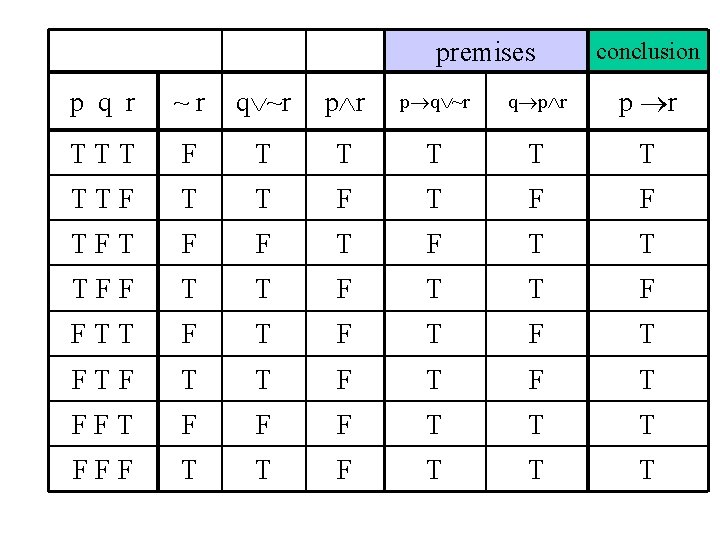
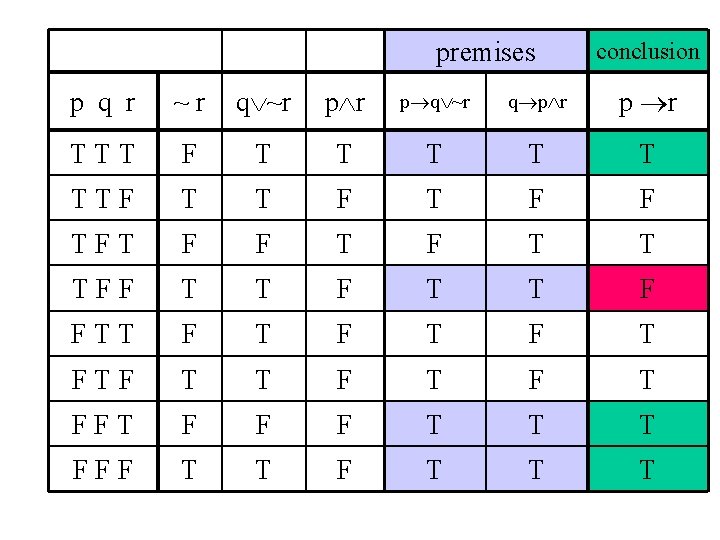
Argument Validity Test Example 1 • p (q r) • ~r • p q

premises p q r TTT TTF TFT TFF FTT FTF FFT FFF q r p (q r) ~r conclusion p q

premises conclusion p q r p (q r) ~r p q TTT T T F T TTF T T TFT T T F T TFF F T T T FTT T T FTF T T FFT T T F F FFF F F T F

premises conclusion p q r p (q r) ~r p q TTT T T F T TTF T T TFT T T F T TFF F T T T FTT T T FTF T T FFT T T F F FFF F F T F

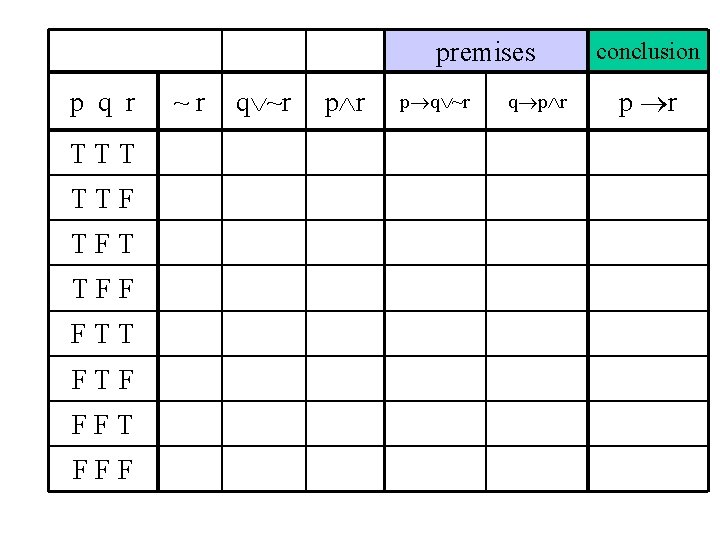
Argument Validity Test Example 2 • p q ~r • q p r • p r

premises p q r TTT TTF TFT TFF FTT FTF FFT FFF ~r q ~r p q ~r q p r conclusion p r

premises conclusion p q r ~r q ~r p q ~r q p r TTT F T T TTF T T F F TFT F F T T TFF T T F FTT F T F T FTF T T F T FFT F F F T T T FFF T T T

premises conclusion p q r ~r q ~r p q ~r q p r TTT F T T TTF T T F F TFT F F T T TFF T T F FTT F T F T FTF T T F T FFT F F F T T T FFF T T T

Rules of Inference (Valid Argument Forms) • • Modus Ponens Modus Tolens Generalization Specialization • • Elimination Transitivity Division into Cases Rule of Contradiction

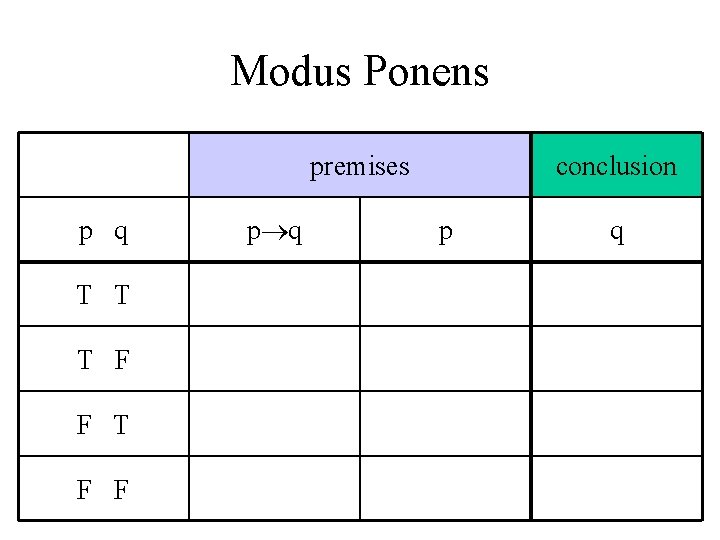
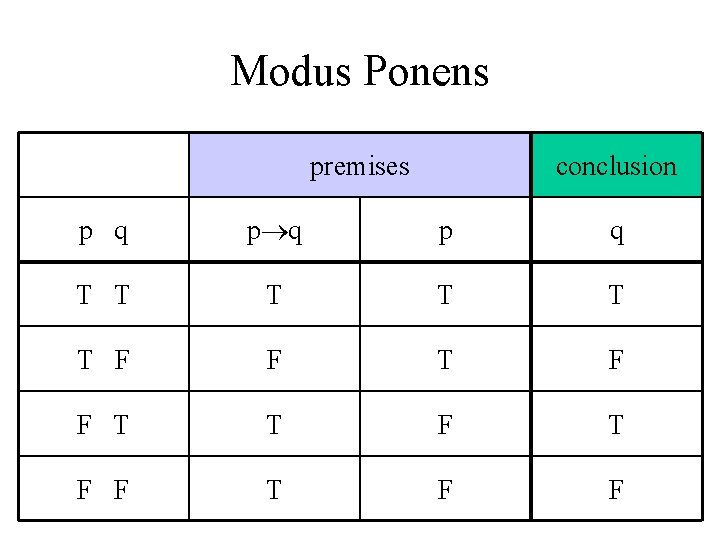
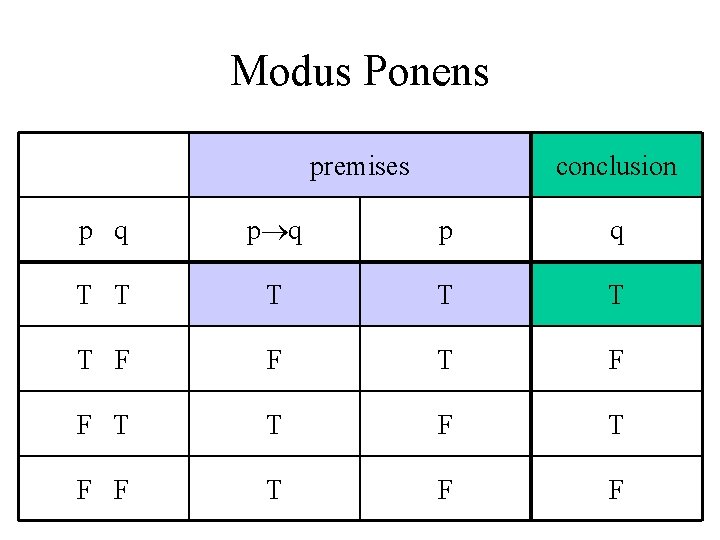
Modus Ponens • If p then q; • p; • q

Modus Ponens premises p q T T T F F p q conclusion p q

Modus Ponens premises conclusion p q p q T T T F F T F F

Modus Ponens premises conclusion p q p q T T T F F T F F

Modus Ponens Example • If the last digit of this number is 0, then the number is divisible by 10. • The last digit of this number is a 0. • This number is divisible by 10.

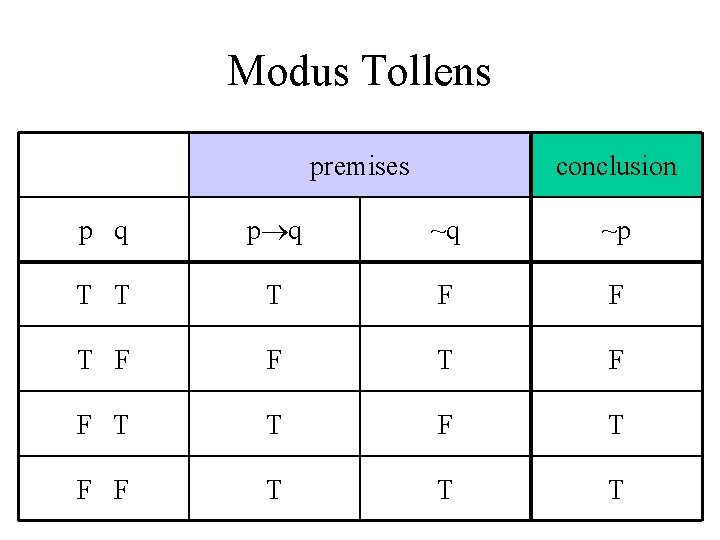
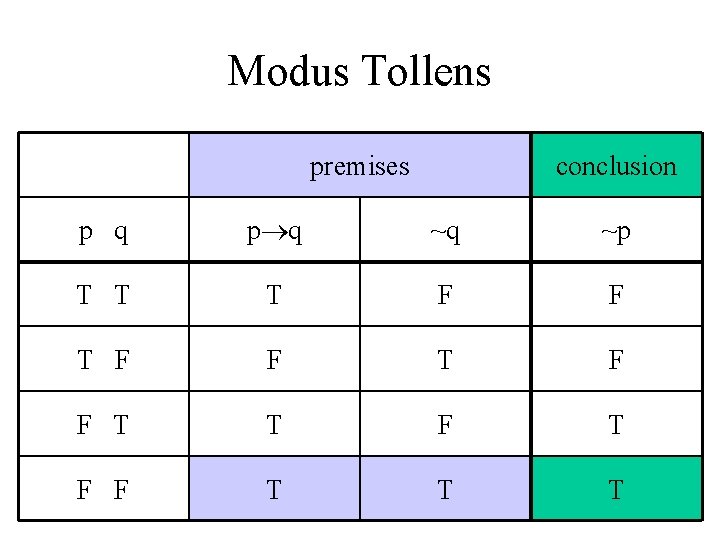
Modus Tollens • If p then q; • ~q; • ~p

Modus Tollens premises p q T T T F F p q conclusion ~q ~p

Modus Tollens premises conclusion p q ~q ~p T T T F F T T F F T T T

Modus Tollens premises conclusion p q ~q ~p T T T F F T T F F T T T

Modus Tollens Example • If Zeus is human, then Zeus is mortal. • Zeus is not mortal. • Zeus is not human • Modus tollens uses the contrapositive.

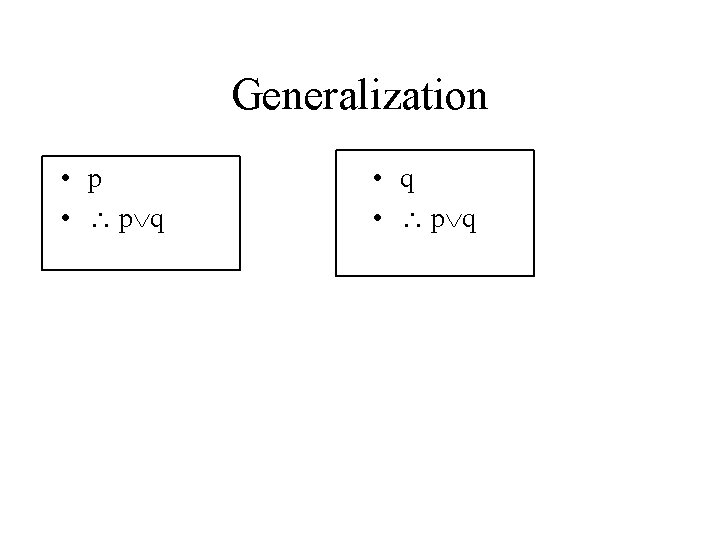
Generalization • p • p q • q • p q

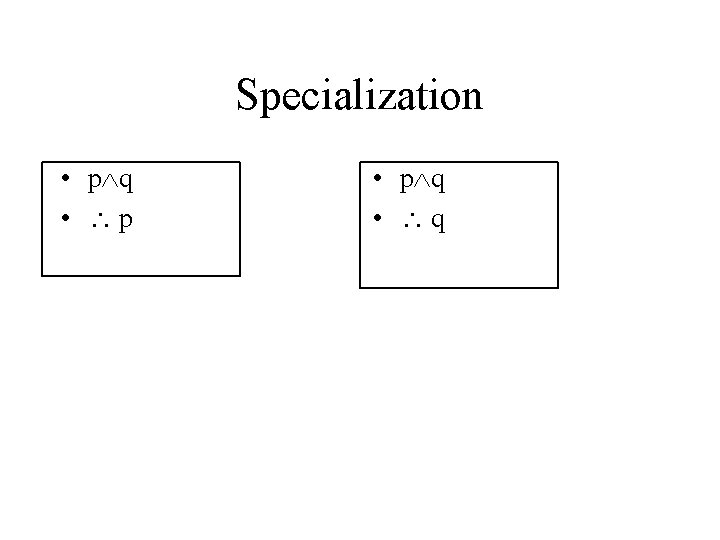
Specialization • p q • p • p q • q

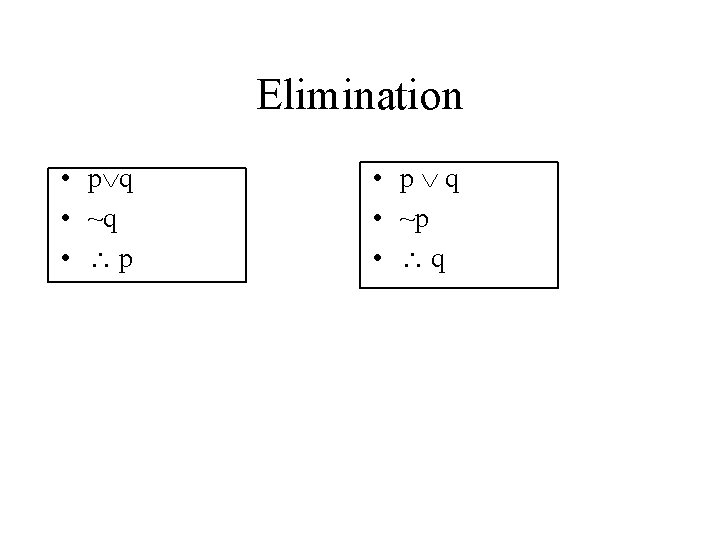
Elimination • p q • ~q • p • p q • ~p • q

Transitivity • p q • q r • p r

Division into Cases • • p q p r q r r

Division into Cases Example • • x>1 or x<-1 If x>1 then x 2>1 If x<-1 then x 2>1

Valid Inference Example Statements a, b, c. • a. If my glasses are on the kitchen table, then I saw them at breakfast. • b. I was reading the newspaper in the living room or I was reading the newspaper in the kitchen. • c. If I was reading the newspaper in the living room, then my glasses are on the coffee table.

Valid Inference Example Statements a, b, c. • a. If my glasses are on the kitchen table, then I saw them at breakfast. • b. I was reading the newspaper in the living room or I was reading the newspaper in the kitchen. • c. If I was reading the newspaper in the living room, then my glasses are on the coffee table.

Valid Inference Example Symbols p, q, r, s, t. • p = My glasses are on the kitchen table. • q = I saw my glasses at breakfast. • r = I was reading the newspaper in the living room • s = I was reading the newspaper in the kitchen. • t = My glasses are on the coffee table.

Statements a, b, c in Symbols • a. p q • b. r s • c. r t

Valid Inference Example Statements d, e, f. • d. I did not see my glasses at breakfast. • e. If I was reading my book in bed, then my glasses are on the bed table. • f. If I was reading the newspaper in the kitchen, then my glasses are on the kitchen table.

Valid Inference Example Statements d, e, f. • d. I did not see my glasses at breakfast. • e. If I was reading my book in bed, then my glasses are on the bed table. • f. If I was reading the newspaper in the kitchen, then my glasses are on the kitchen table.

Valid Inference Example Symbols u, v. • u =I was reading my book in bed. • v = My glasses are on the bed table.

Statements d, e, f in Symbols • d. ~q • e. u v • f. s p

Inference Example Givens • a. p q • b. r s • c. r t • d. ~q • e. u v • f. s p

Deduction Sequence • 1. p q ~q ~p • 2. s p ~p ~s from ( ) by _____ from ( ) by_____

Deduction Sequence • 1. p q ~q ~p • 2. s p ~p ~s from (a) from (d) by modus tollens from (f) from (1) by modus tollens

Deduction Sequence • 3. r s ~s r • 4. r t r t from ( ) by_____________

Deduction Sequence • 3. r s ~s r • 4. r t r t from (b) from (2) by disjunctive syllogism from (c) from (3) by modus ponens

Errors in Reasoning • • • Using vague or ambiguous premises. Circular reasoning Jumping to conclusions Converse error Inverse error

Converse Error • If Zeke is a cheater, then Zeke sits in the back row. Zeke is a cheater. • p q q p

Inverse Error • If interest rates are going up, then stock market prices will go down. Interest rates are not going up Stock market prices will not go down. • p q ~p ~q

Inverse Error • If I intend to sell my house, then I will need a permit for this wall. I do not intend to sell my house. I do not need a permit for this wall. • p q ~p ~q

Validity vs. Truth • Valid arguments can have false conclusions if one of the premises is false. • Invalid arguments can have true conclusions.

Valid but False • If John Lennon was a rock star then John Lennon had red hair. • John Lennon was a rock star. • John Lennon had red hair.

Invalid but True • If New York is a big city, then New York has tall buildings. • New York is a big city.

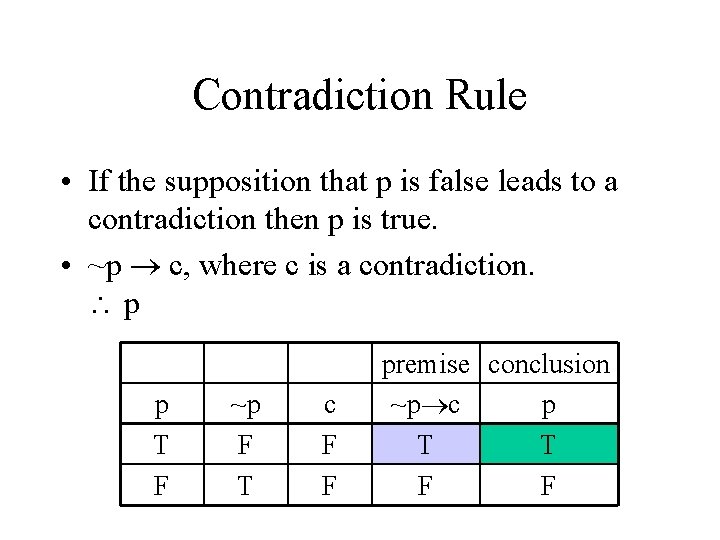
Contradiction Rule • If the supposition that p is false leads to a contradiction then p is true. • ~p c, where c is a contradiction. p

Contradiction Rule • If the supposition that p is false leads to a contradiction then p is true. • ~p c, where c is a contradiction. p p T F ~p F T c F F premise conclusion ~p c p T T F F

Rule of Contradiction Example • • Knights tell the truth, Knaves lie. A says: “B is a knight. ” B says: “A and I are opposite types. ” What are A and B? • (Hint: Suppose A is a Knight. )

Rules of Inference (Valid Argument Forms) • • Modus Ponens Modus Tolens Disjunctive Addition Conjunctive Simplification • Disjunctive Syllogism • Hypothetical Syllogism • Division into Cases • Rule of Contradiction