v Standard Model goes pearshaped in CERN experiment

v Standard Model goes pear-shaped in CERN experiment The Register v Physicists get a good look at pear-shaped atomic nuclei The Los Angeles Times v Exotic atoms could explain why Big Bang created more matter Newstrack India The lopsided nuclei, described today (May 8) in the journal Nature, could be good candidates for researchers looking for new types of physics beyond the reigning explanation for the bits of matter that make up the universe (called the Standard Model), said study author Peter Butler, a physicist at the University of Liverpool in the United Kingdom. The findings could help scientists search for physics beyond the Standard model, said Witold Nazarewicz. An electric dipole moment would provide a way to test extension theories to the Standard Model, such as supersymmetry, which could help explain why there is more matter than antimatter in the universe. Until now, only one pear-shaped nucleus had been found experimentally: radium 226, whose shape was sketched out back in 1993. H. J. Wollersheim, H. Emling, H. Grein, R. Kulessa, R. S. Simon, C. Fleischmann, J. de Boer, E. Hauber, C. Lauterbach, C. Schandera, P. A. Butler, T. Czosnyka; Nucl. Phys. A 556, 261 (1993).

The Standard Model describes four fundamental forces or interactions „If equal amounts of matter and antimatter were created at the Big Bang, everything would have been annihilated, and there would be no galaxies, stars, planets or people“ (Tim Chupp Univ. Michigan)

I II III Three Generations of Matter Force Carriers Gauge bosons Leptons Quarks Elementary Particles

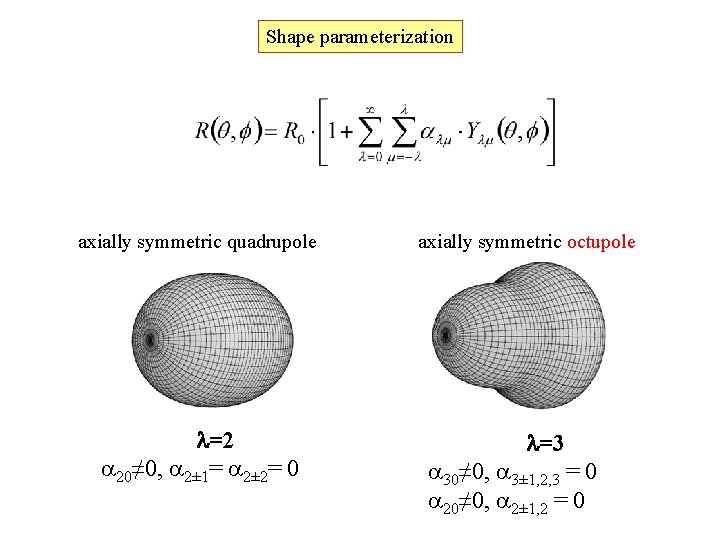
Shape parameterization axially symmetric quadrupole l=2 a 20≠ 0, a 2± 1= a 2± 2= 0 axially symmetric octupole l=3 a 30≠ 0, a 3± 1, 2, 3 = 0 a 20≠ 0, a 2± 1, 2 = 0

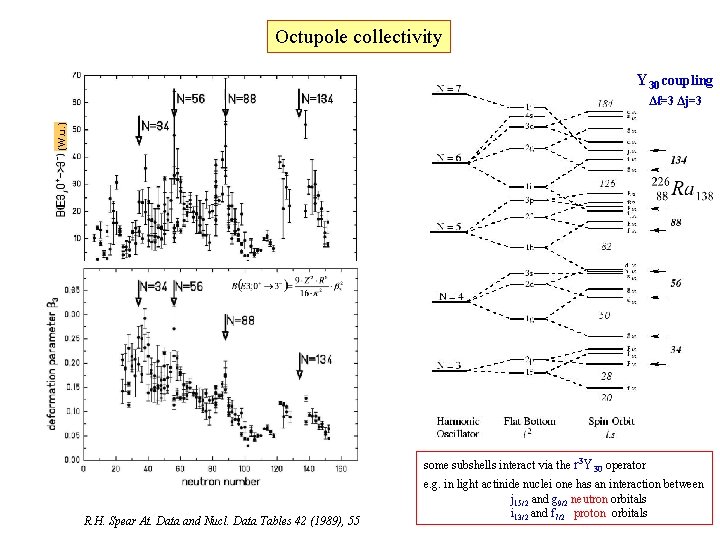
Octupole collectivity Y 30 coupling (W. u. ) Δℓ=3 Δj=3 some subshells interact via the r 3 Y 30 operator R. H. Spear At. Data and Nucl. Data Tables 42 (1989), 55 e. g. in light actinide nuclei one has an interaction between j 15/2 and g 9/2 neutron orbitals i 13/2 and f 7/2 proton orbitals

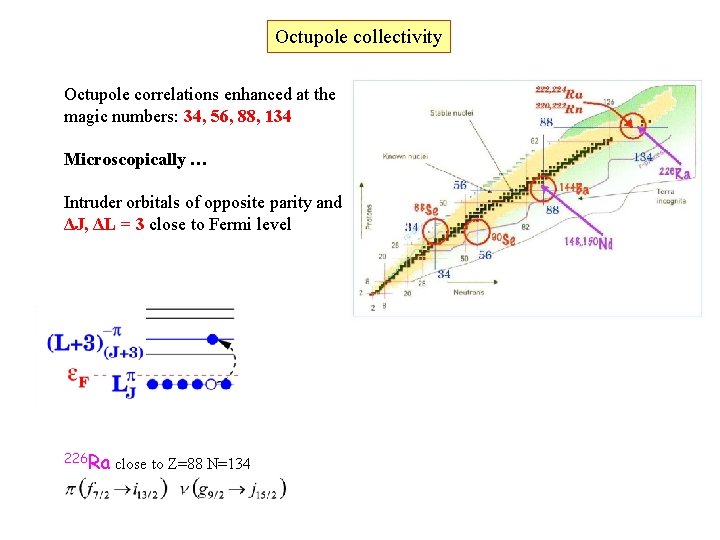
Octupole collectivity Octupole correlations enhanced at the magic numbers: 34, 56, 88, 134 Microscopically … Intruder orbitals of opposite parity and ΔJ, ΔL = 3 close to Fermi level 226 Ra close to Z=88 N=134

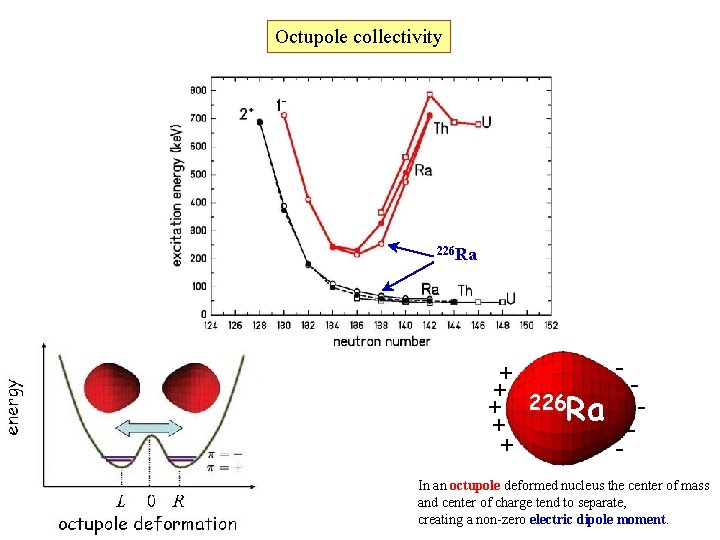
Octupole collectivity 226 Ra + + + 226 Ra + + In an octupole deformed nucleus the center of mass and center of charge tend to separate, creating a non-zero electric dipole moment.

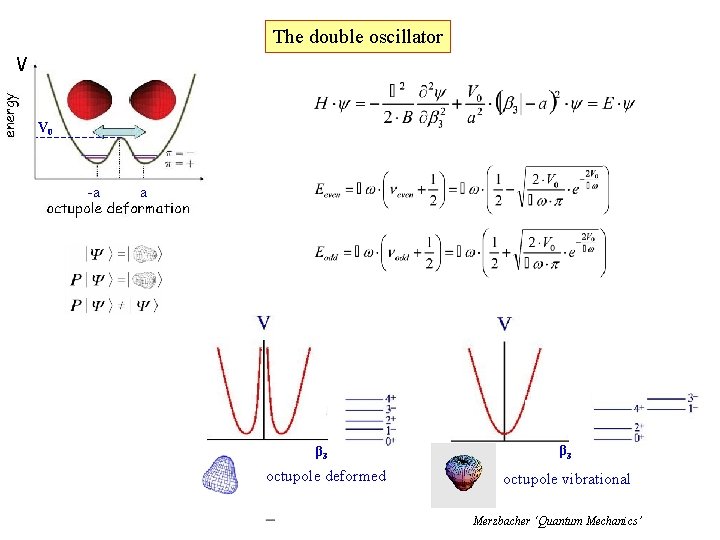
The double oscillator V V 0 -a a β 3 octupole deformed β 3 octupole vibrational Merzbacher ‘Quantum Mechanics’

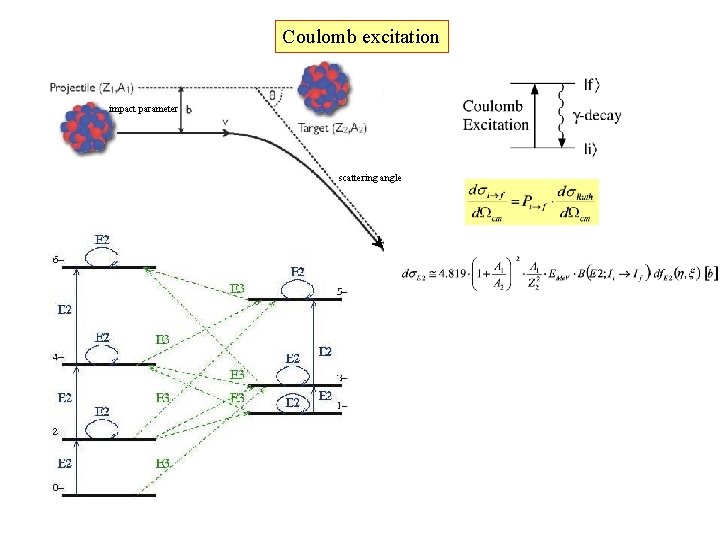
Coulomb excitation impact parameter scattering angle

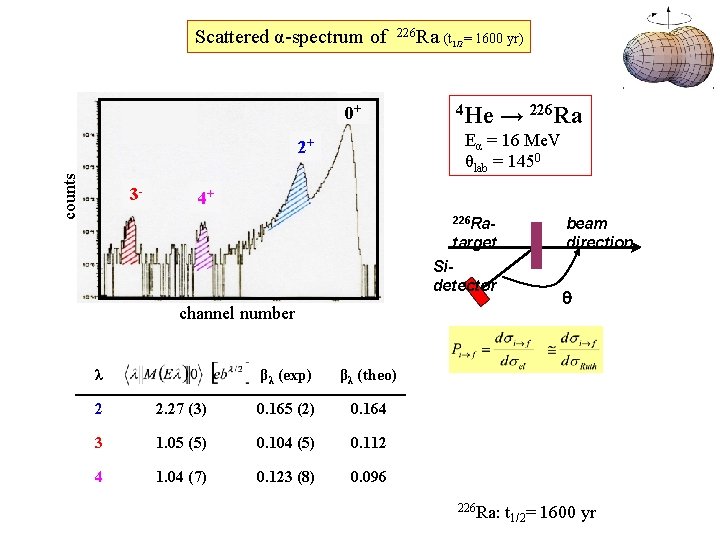
Scattered α-spectrum of 226 Ra (t = 1600 yr) 1/2 0+ counts → 226 Ra Eα = 16 Me. V θlab = 1450 2+ 3 - 4 He 4+ 226 Ra- target Sidetector channel number λ βλ (exp) βλ (theo) 2 2. 27 (3) 0. 165 (2) 0. 164 3 1. 05 (5) 0. 104 (5) 0. 112 4 1. 04 (7) 0. 123 (8) 0. 096 226 Ra: beam direction q t 1/2= 1600 yr

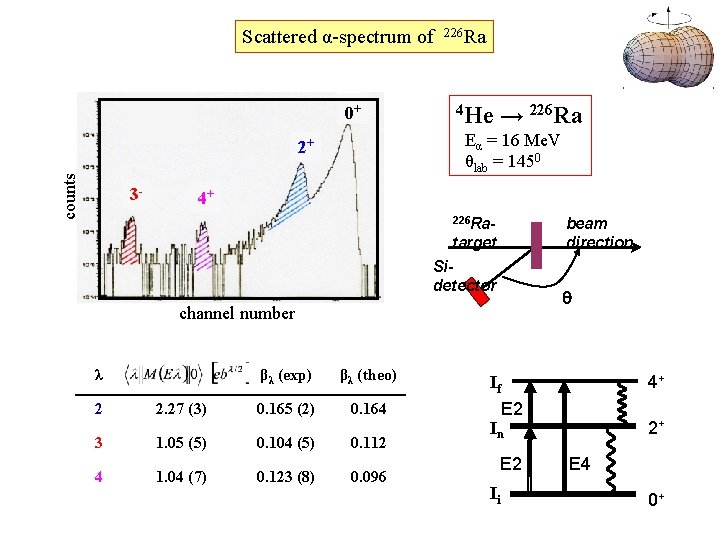
Scattered α-spectrum of 0+ counts 4 He → 226 Ra Eα = 16 Me. V θlab = 1450 2+ 3 - 226 Ra 4+ 226 Ra- beam direction target Sidetector q channel number λ 2 2. 27 (3) βλ (exp) βλ (theo) 0. 165 (2) 0. 164 3 1. 05 (5) 0. 104 (5) 0. 112 4 1. 04 (7) 0. 123 (8) 0. 096 4+ If E 2 2+ In E 2 Ii E 4 0+

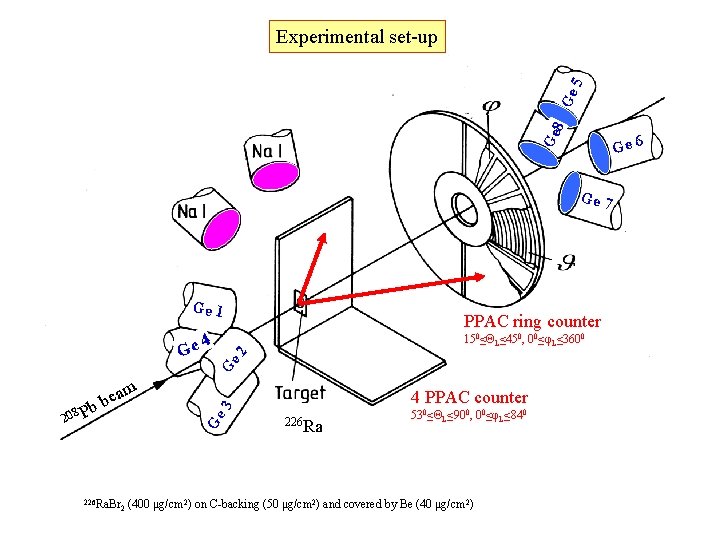
Ge 8 Ge 5 Experimental set-up Ge 6 Ge 7 Ge 1 G G 150≤ΘL≤ 450, 00≤φL≤ 3600 e 2 e 4 PPAC ring counter 226 Ra. Br 2 4 PPAC counter 3 Ge eam b b 208 P 226 Ra 530≤ΘL≤ 900, 00≤φL≤ 840 (400 μg/cm 2) on C-backing (50 μg/cm 2) and covered by Be (40 μg/cm 2)

Coulomb excitation of 226 Ra

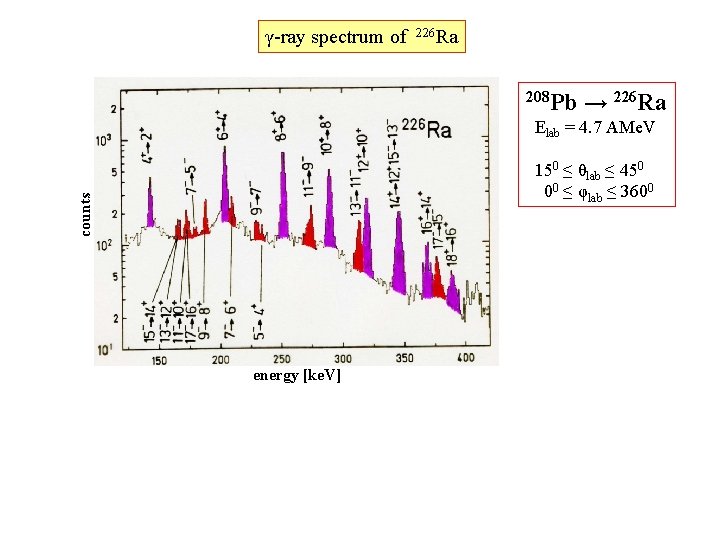
γ-ray spectrum of 226 Ra 208 Pb → 226 Ra Elab = 4. 7 AMe. V counts 150 ≤ θlab ≤ 450 00 ≤ φlab ≤ 3600 energy [ke. V]

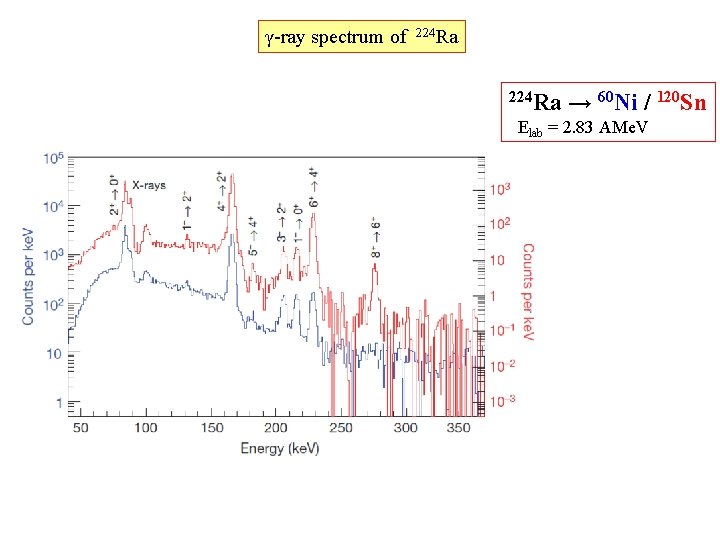
γ-ray spectrum of 224 Ra → 60 Ni / 120 Sn Elab = 2. 83 AMe. V

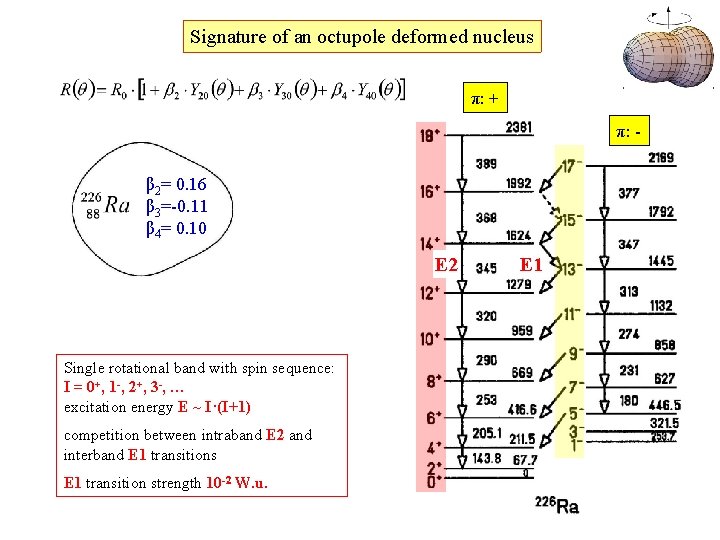
Signature of an octupole deformed nucleus π: + π: β 2= 0. 16 β 3=-0. 11 β 4= 0. 10 E 2 Single rotational band with spin sequence: I = 0+, 1 -, 2+, 3 -, … excitation energy E ~ I·(I+1) competition between intraband E 2 and interband E 1 transitions E 1 transition strength 10 -2 W. u. E 1

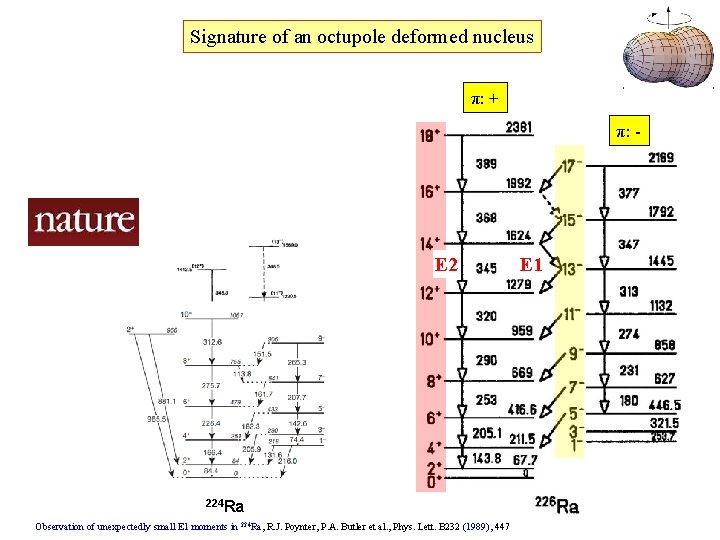
Signature of an octupole deformed nucleus π: + π: - E 2 224 Ra Observation of unexpectedly small E 1 moments in 224 Ra, R. J. Poynter, P. A. Butler et al. , Phys. Lett. B 232 (1989), 447 E 1

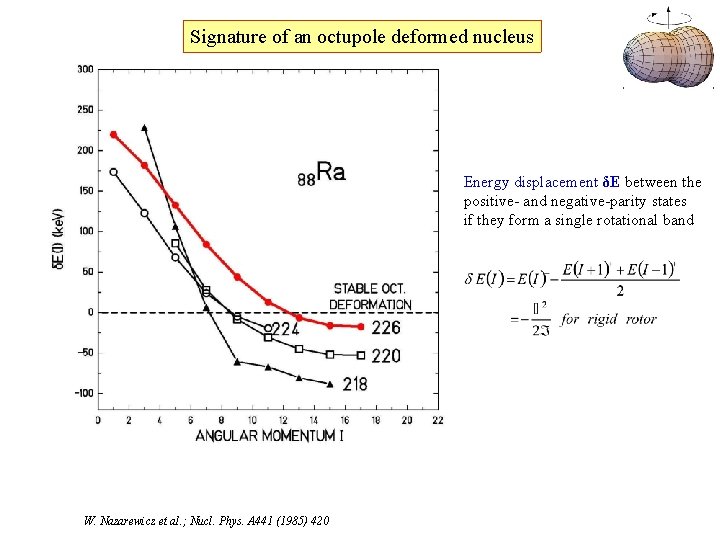
Signature of an octupole deformed nucleus Energy displacement δE between the positive- and negative-parity states if they form a single rotational band W. Nazarewicz et al. ; Nucl. Phys. A 441 (1985) 420

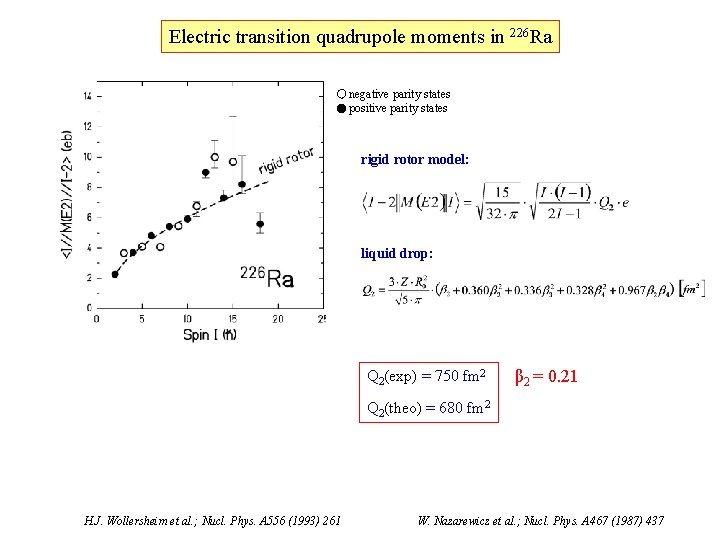
Electric transition quadrupole moments in 226 Ra negative parity states positive parity states rigid rotor model: liquid drop: Q 2(exp) = 750 fm 2 β 2 = 0. 21 Q 2(theo) = 680 fm 2 H. J. Wollersheim et al. ; Nucl. Phys. A 556 (1993) 261 W. Nazarewicz et al. ; Nucl. Phys. A 467 (1987) 437

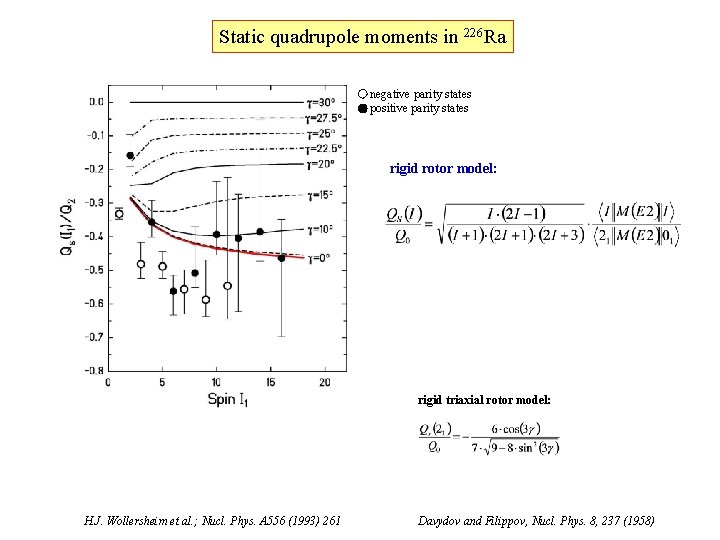
Static quadrupole moments in 226 Ra negative parity states positive parity states rigid rotor model: rigid triaxial rotor model: H. J. Wollersheim et al. ; Nucl. Phys. A 556 (1993) 261 Davydov and Filippov, Nucl. Phys. 8, 237 (1958)

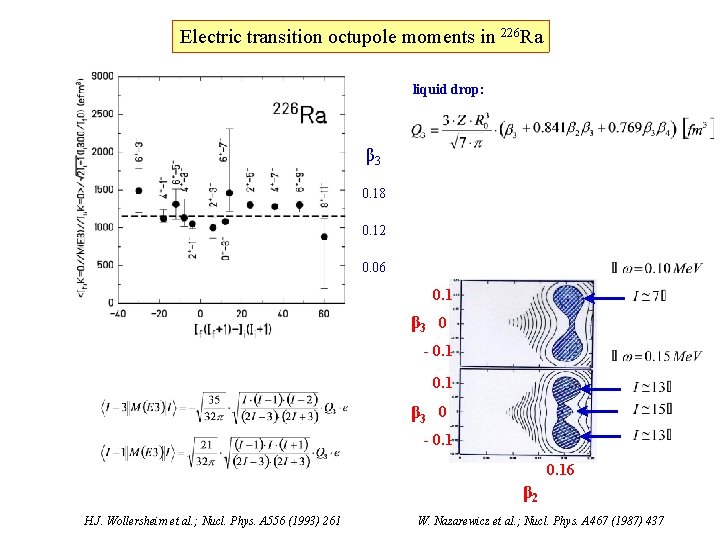
Electric transition octupole moments in 226 Ra liquid drop: β 3 0. 18 0. 12 0. 06 0. 1 β 3 0 - 0. 16 β 2 H. J. Wollersheim et al. ; Nucl. Phys. A 556 (1993) 261 W. Nazarewicz et al. ; Nucl. Phys. A 467 (1987) 437

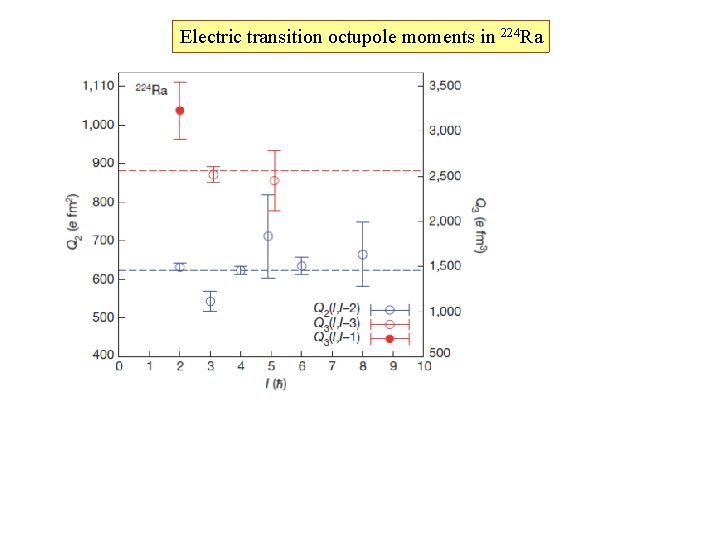
Electric transition octupole moments in 224 Ra

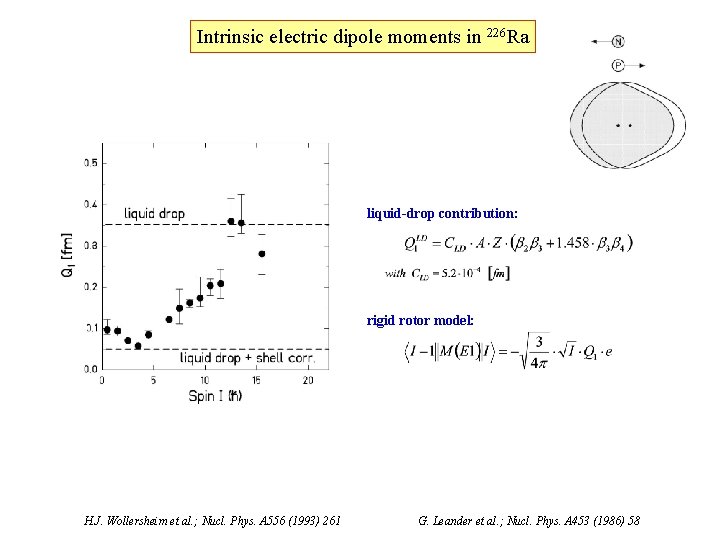
Intrinsic electric dipole moments in 226 Ra liquid-drop contribution: rigid rotor model: H. J. Wollersheim et al. ; Nucl. Phys. A 556 (1993) 261 G. Leander et al. ; Nucl. Phys. A 453 (1986) 58

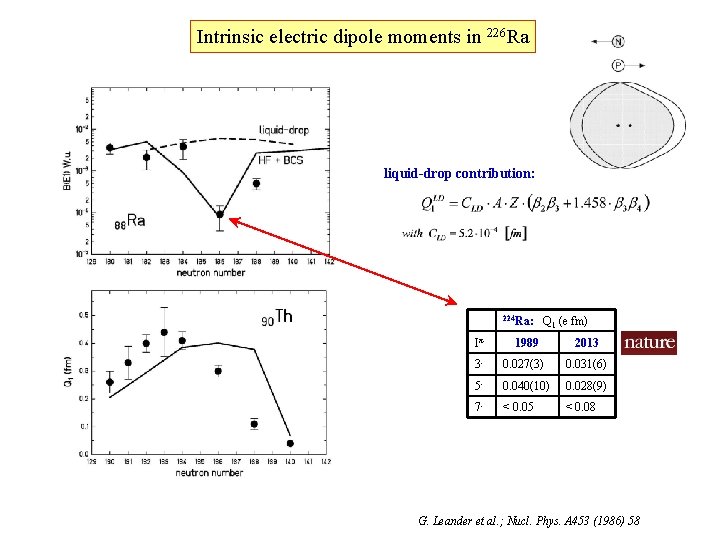
Intrinsic electric dipole moments in 226 Ra liquid-drop contribution: 224 Ra: Q 1 (e fm) Iπ 1989 2013 3 - 0. 027(3) 0. 031(6) 5 - 0. 040(10) 0. 028(9) 7 - < 0. 05 < 0. 08 G. Leander et al. ; Nucl. Phys. A 453 (1986) 58

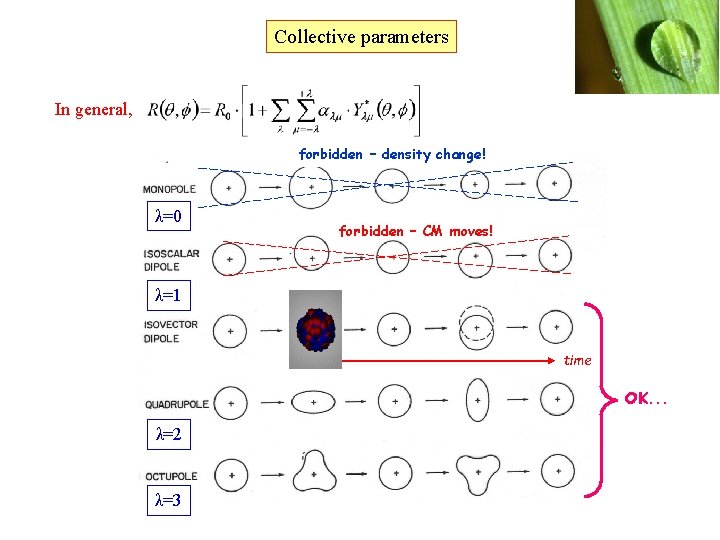
Collective parameters In general, forbidden – density change! λ=0 forbidden – CM moves! λ=1 time OK. . . λ=2 λ=3

Center of mass conservation The coordinates (x, y, z) can be expressed by The dipole coordinate is not an independent quantity. It is non-zero for nuclear shapes with both quadrupole and octupole degrees of freedom.

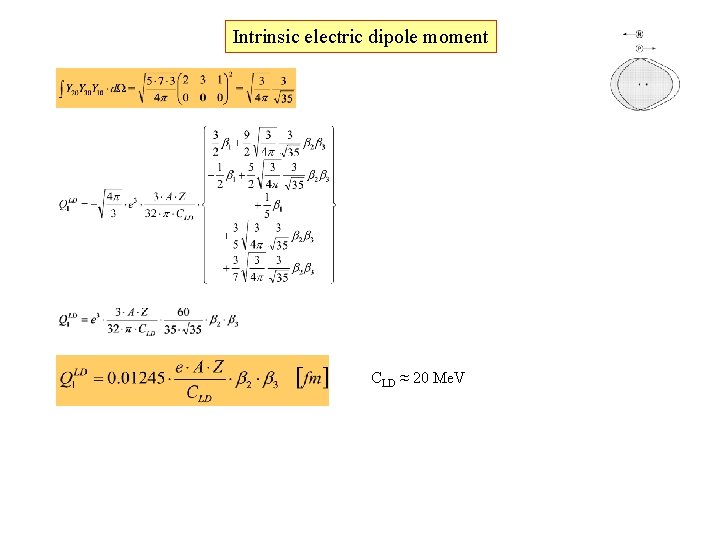
Intrinsic electric dipole moment The local volume polarization of electric charge can be derived from the requirement of a minimum in the energy functional. (Myers Ann. of Phys. (1971)) where ρp and ρn are the proton and neutron densities, CLD is the volume symmetry energy coefficient of the liquid drop model and VC is the Coulomb potential generated by ρp inside the nucleus (r < R 0) Keeping the center of gravity fixed, the integral

Intrinsic electric dipole moment

Intrinsic electric dipole moment CLD ≈ 20 Me. V

Summary Ø single rotational band for Ø no backbending observed Ø β 2, β 3, β 4 deformation parameters are in excellent agreement with calculated values Ø octupole deformation is three times larger than in octupolevibrational nuclei Ø equal transition quadrupole moments for positive- and negativeparity states Ø static quadrupole moments are in excellent agreement with an axially symmetric shape Ø electric dipole moments are close to liquid-drop value ( ) Ø octupole deformation seems to be stabilized with increasing rotational frequency

Coulomb excitation of 226 Ra target broken after 8 hours Christoph Fleischmann