V PENYEDERHANAAN PERSAMAAN LOGIKA A DIAGRAM Adalah untuk

V. PENYEDERHANAAN PERSAMAAN LOGIKA A. DIAGRAM Adalah untuk menggambarkan prinsip atau dasar logika melalui set / himpunan. Gambar diagram Venn 1. Untuk n = 1 S A’ A

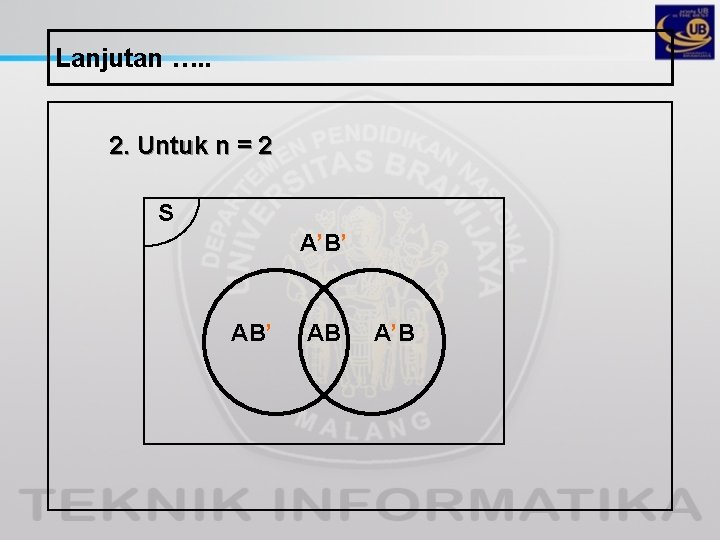
Lanjutan …. . 2. Untuk n = 2 S A’B’ AB A’B

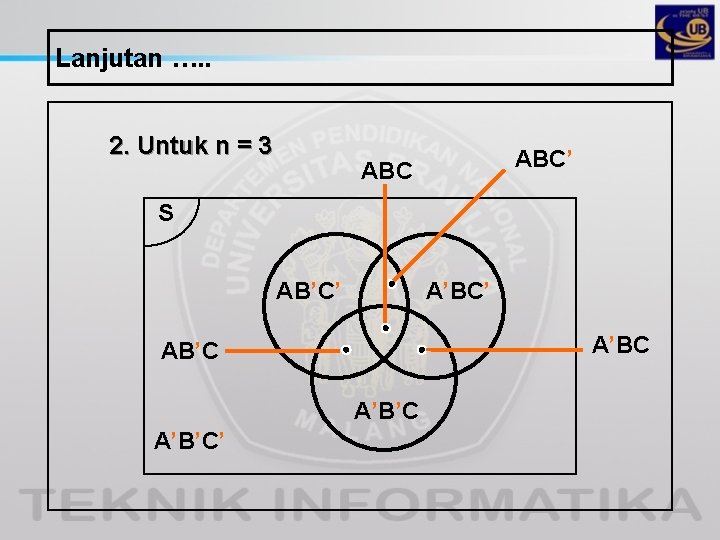
Lanjutan …. . 2. Untuk n = 3 ABC’ ABC S AB’C’ A’BC AB’C A’B’C’

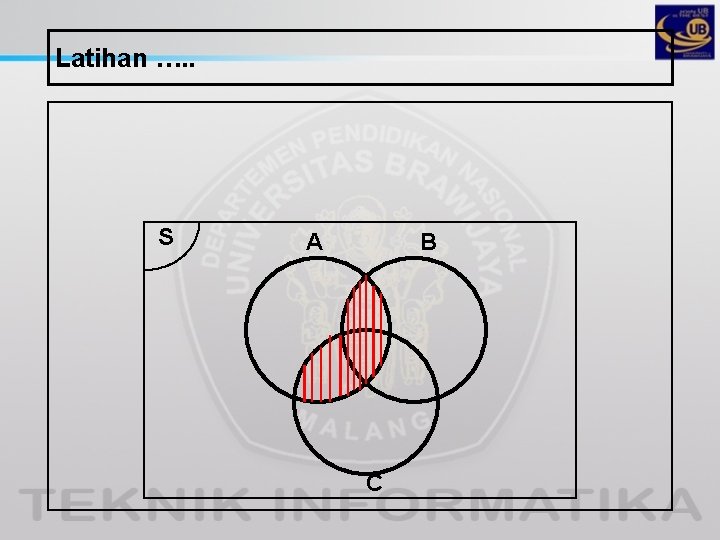
Latihan …. . S A B C

B. PETA KARNAUGHT Metode peta karnaught untuk menyederhana kan persamaan logika. Peta Karnaught dengan 2 variabel f(AB) B’ A’ A B A’ B’ A’ B AB b. Peta Karnaught dengan 3 variabel f (ABC) A’ A B’C’ B’C A’B’C’ A’B’C AB’C’ AB’C BC A’BC ABC BC’ A’BC’ ABC’

Lanjutan …. . c. Peta Karnaught dengan 4 variabel f(ABCD) C’D’ A’B AB AB’ C’D CD CD’

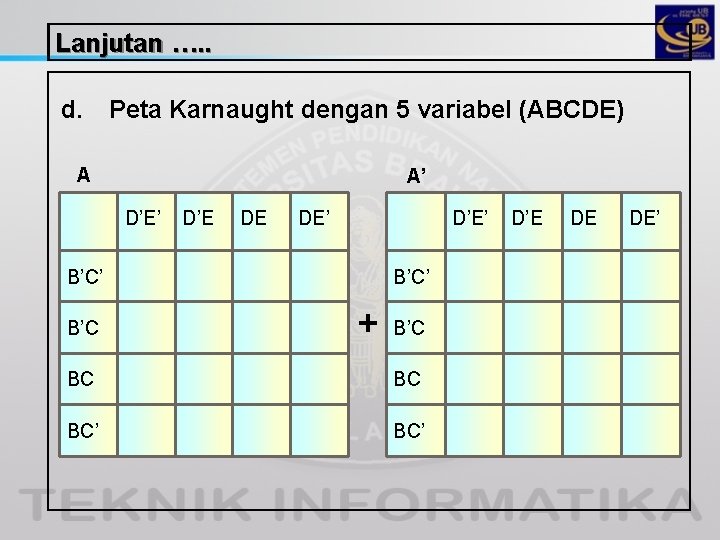
Lanjutan …. . d. Peta Karnaught dengan 5 variabel (ABCDE) A A’ D’E DE DE’ D’E’ B’C B’C’ + B’C BC BC BC’ D’E DE DE’

e. APLIKASI PETA KARNAUGHT UNTUK MENYEDERHANAKAN PERSAMAAN LOGIKA. a. Minimimasi persamaan logika dalam bentuk kemonis SOP ( MINTERM ) dengan peta karnaught b. Minimasi persamaan logika dalam bentuk Kemonis POS ( MAXTERM ) dengan peta karnaught c. Bentuk yang dapat di sederhanakan untuk mengeliminasi multi variabel

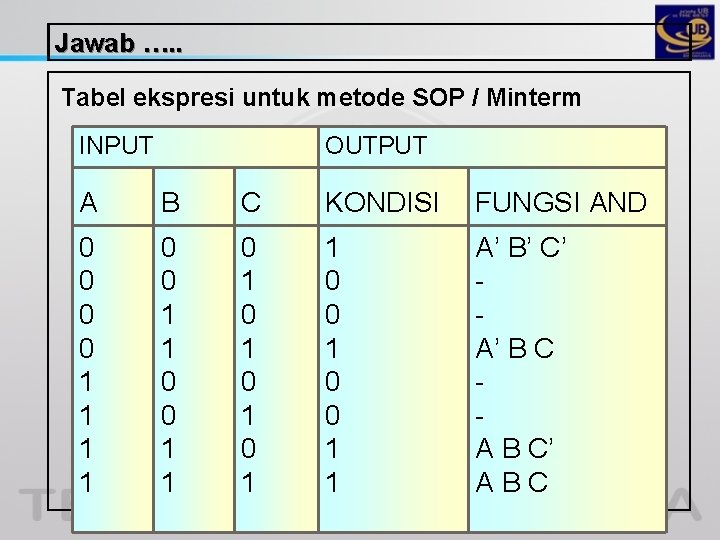
VI. PENYEDERHANAAN PERSAMAAN LOGIKA A. REPRESENTASI KANONIKAL SUM OF PRODUCT ( SOP ) Merupakan ekspresi fungsi AND atau metode SOP - Rangkaian kombinasi logika - Kondisi output ditentukan oleh kombinasi input – inputnya Contoh : Buatlah persamaan boolean dan rangkaian logika dari fungsi boolean dalam bentuk Minterm sbb : F(ABC) = ∑ ( 0, 3, 6, 7 )

Jawab …. . Tabel ekspresi untuk metode SOP / Minterm INPUT OUTPUT A B C KONDISI FUNGSI AND 0 0 1 1 0 1 0 1 1 0 0 1 1 A’ B’ C’ A’ B C A B C’ ABC

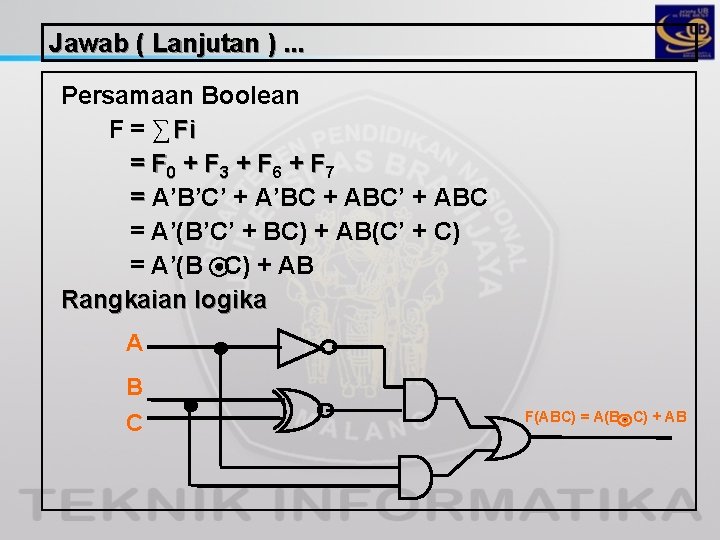
Jawab ( Lanjutan ). . . Persamaan Boolean F = ∑ Fi = F 0 + F 3 + F 6 + F 7 = A’B’C’ + A’BC + ABC’ + ABC = A’(B’C’ + BC) + AB(C’ + C) = A’(B C) + AB Rangkaian logika A B C F(ABC) = A(B C) + AB

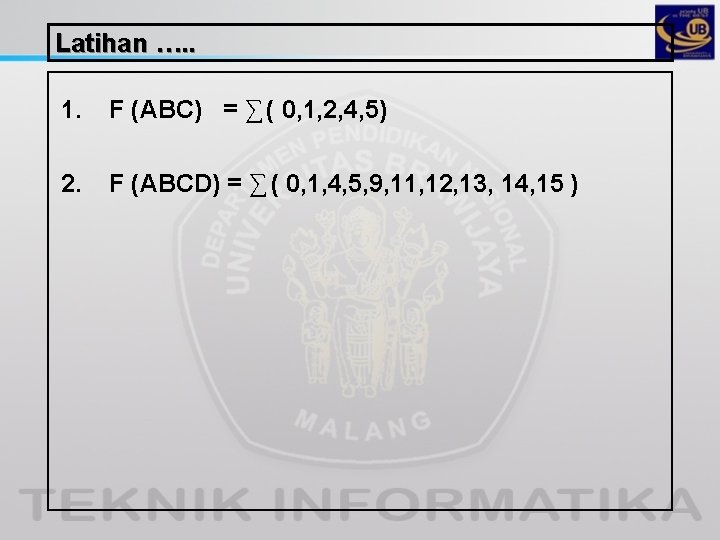
Latihan …. . 1. F (ABC) = ∑ ( 0, 1, 2, 4, 5) 2. F (ABCD) = ∑ ( 0, 1, 4, 5, 9, 11, 12, 13, 14, 15 )

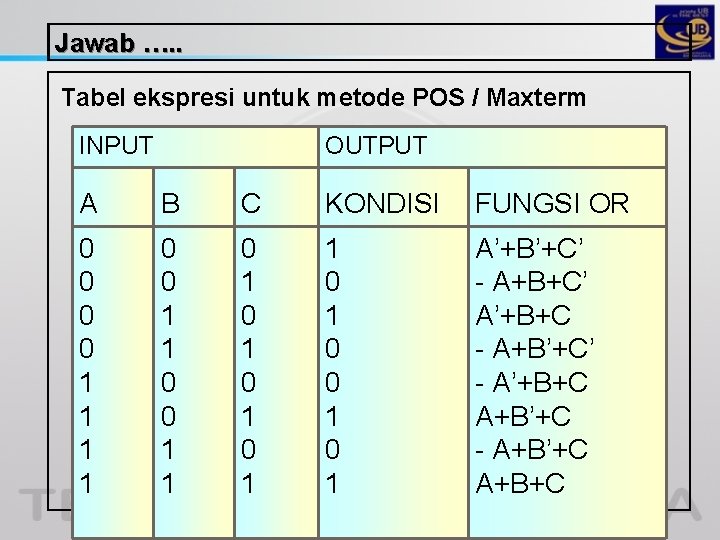
B. REPRESENTASI KANONIKAL PRODUCT OF SUM ( POS ) Merupakan ekspresi fungsi OR atau metode POS - Rangkaian kombinasi logika - Kondisi output ditentukan oleh kombinasi input – inputnya Contoh : Buatlah persamaan boolean dan rangkaian logika dari fungsi boolean dalam bentuk MAXTERM sbb : F(ABC) = Π ( 0, 2, 5, 7 )

Jawab …. . Tabel ekspresi untuk metode POS / Maxterm INPUT OUTPUT A B C KONDISI FUNGSI OR 0 0 1 1 0 1 0 1 1 0 0 1 A’+B’+C’ - A+B+C’ A’+B+C - A+B’+C’ - A’+B+C A+B’+C - A+B’+C A+B+C

Jawab ( Lanjutan ). . . Persamaan Boolean F = π Fi = F 0 • F 2 • F 5 • F 7 = (A’+B’+C’) • (A’+B+C’) • (A+B’+C) • (A+B+C) ( = (A’+C’) • (A+C) = A’C + AC’ =A⊕ C Rangkaian logika A C F(ABC) = A ⊕ C

Latihan …. . 1. F (ABC) = π ( 1, 3, 7 ) 2. F (ABCD) = π ( 3, 8, 10, 11, 15 )

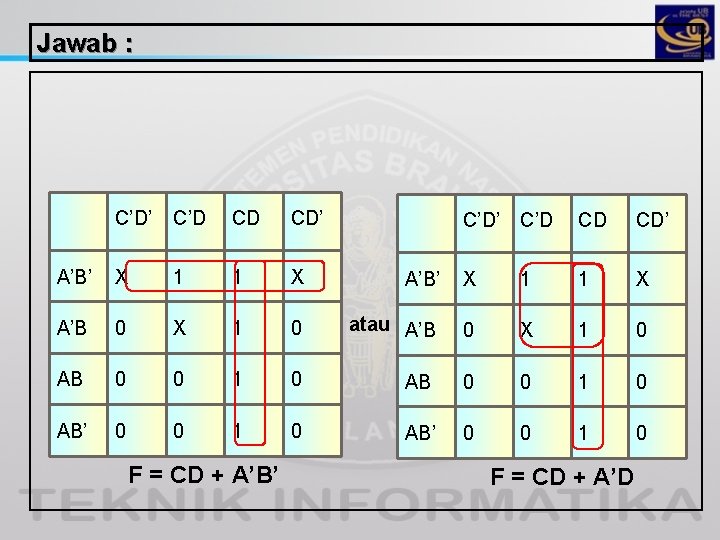
C. DON’T CARE CONDITION Kondisi Don’t Care adalah suatu kondisi yang Ko dapat diasumsikan mempunyai keadaan 0 atau 1 yang juga ditandai dengan X dan untuk menyederhanakan ekspresi boolean menggunakan peta. Contoh : Sederhanakan fungsi Boolean sbb : F(A, B, C, D) = ∑ ( 1, 3, 7, 11, 15 ) Yang mempunyai don’t care condition sbb : d(A, B, C, D) = ∑ ( 0, 2, 5 )

Jawab : C’D’ C’D CD CD’ A’B’ X 1 1 X A’B 0 X 1 AB 0 0 AB’ 0 0 C’D’ C’D CD CD’ A’B’ X 1 1 X 0 atau A’B 0 X 1 0 AB 0 0 1 0 AB’ 0 0 1 0 F = CD + A’B’ F = CD + A’D