v CHAPTER 1 INTEREST MEASUREMENT INTEREST RATE DEFINITIONS
















- Slides: 20

v CHAPTER 1 INTEREST MEASUREMENT: INTEREST RATE DEFINITIONS FORCE OF INTEREST TWO EXCEPTIONS (SIMPLE INTEREST AND VARIABLE FOI) TIME VALUE OF MONEY v Salma Alsuwailem

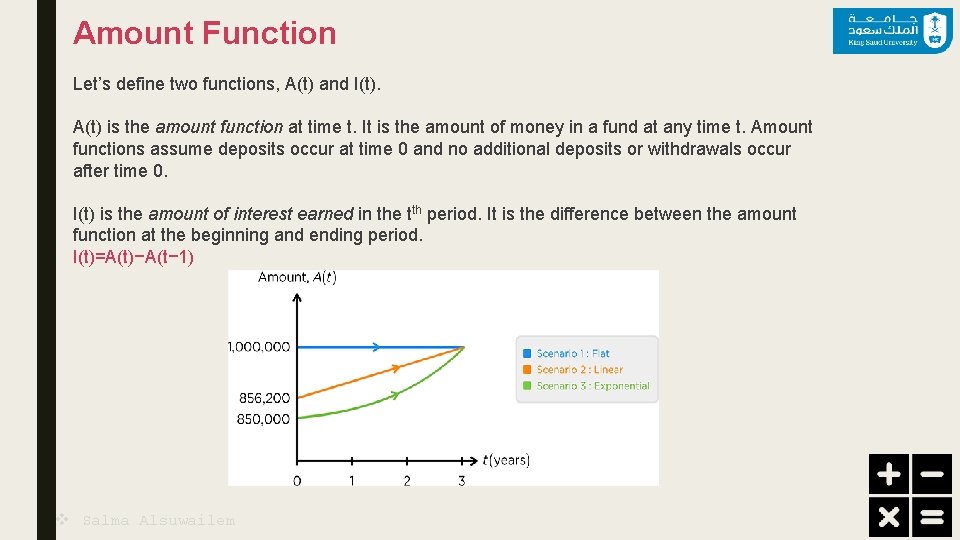
Amount Function Let’s define two functions, A(t) and I(t). A(t) is the amount function at time t. It is the amount of money in a fund at any time t. Amount functions assume deposits occur at time 0 and no additional deposits or withdrawals occur after time 0. I(t) is the amount of interest earned in the tth period. It is the difference between the amount function at the beginning and ending period. I(t)=A(t)−A(t− 1) v Salma Alsuwailem

Albert Einstein famously stated: “Compound interest is the eighth wonder of the world. He who understands it, earns it. . . he who doesn’t. . . pays it. ” v Salma Alsuwailem

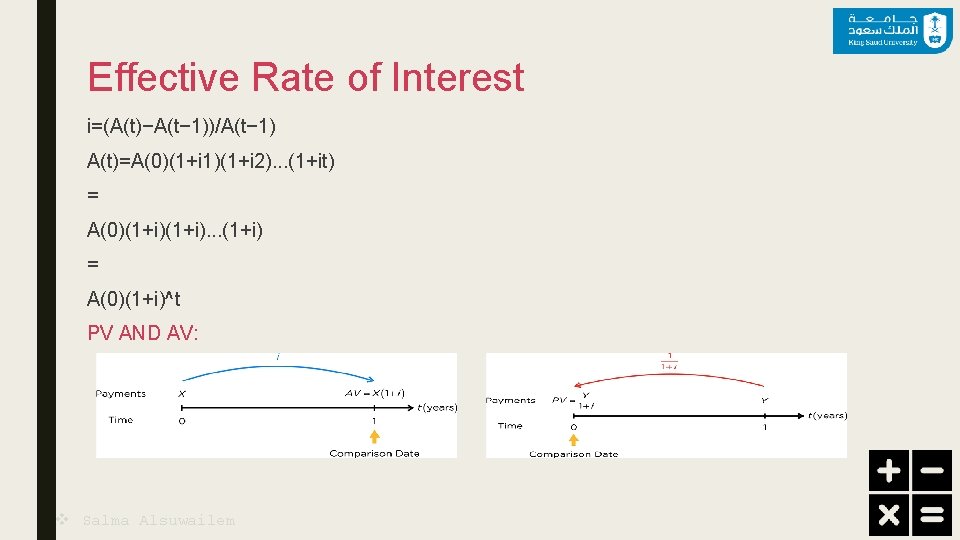
Effective Rate of Interest i=(A(t)−A(t− 1))/A(t− 1) A(t)=A(0)(1+i 1)(1+i 2). . . (1+it) = A(0)(1+i). . . (1+i) = A(0)(1+i)^t PV AND AV: v Salma Alsuwailem

Example: You are given the following amount function: A(t)=t^2+100 Suppose $50 was invested at t = 4. What would be its accumulated value at t = 6 ? A 53. 80 B 57. 20 C 58. 60 D 61. 50 E 66. 00 v Salma Alsuwailem

Example: Fund A is invested at an annual effective interest rate of 3%. Fund B is invested at an annual effective interest rate of 2. 5%. At the end of 20 years, the total in the two funds is 10, 000. At the end of 31 years, the amount in Fund A is twice the amount in Fund B. Calculate the total in the two funds at the end of 10 years. A 5, 732 B 6, 602 C 7, 472 D 7, 569 E 8, 123 v Salma Alsuwailem

Effective Rate of Discount: dt=(A(t)−A(t− 1))/A(t)=A(0)(1−d 1)^-1(1−d 2)^-1. . . (1−dt)^-1 =A(0)(1−d)^-1. . . (1−d)^-1 =A(0)(1−d)^-t Nominal Rate of Interest: (1+j)^m=(1+(i(m)/m))^m=(1+i) Nominal Rate of Discount: (1−k)^m=(1−(d(m)/m))^m=(1−d) v Salma Alsuwailem

Examples: On January 1, 1980, Jack deposited 1, 000 into Bank X to earn interest at the rate of j per annum compounded semi-annually. On January 1, 1985, he transferred his account to Bank Y to earn interest at the rate of k per annum compounded quarterly. On January 1, 1988, the balance at Bank Y is 1, 990. 76. If Jack could have earned interest at the rate of k per annum compounded quarterly from January 1, 1980 through January 1, 1988, his balance would have been 2, 203. 76. Calculate the ratio k/j. A 1. 25 B 1. 30 C 1. 35 D 1. 40 E 1. 45 v Salma Alsuwailem

John invests 1, 000 in a fund which earns interest during the first year at a nominal rate of K convertible quarterly. During the second year, the fund earns interest at a nominal discount rate of K convertible quarterly. At the end of the second year, the fund has accumulated to 1, 173. 54. Calculate K. A 0. 064 B 0. 068 C 0. 072 D 0. 076 E 0. 080 v Salma Alsuwailem

Force of Interest Accumulation Function of Constant Force of Interest Recall the accumulation function for a constant effective interest rate is: a(t)=(1+i)^t Let's solve for 1+i to identify the equivalent accumulation factor in terms of δ: δ=ln(1+i) a(t)=e^δt Variable Force of Interest a(t)=e^∫δudu δt=a′(t)/a(t) v Salma Alsuwailem

Examples: At time, t=0, Billy puts 625 into an account paying 6% simple interest. At the end of year 2, George puts 400 into an account paying interest at a force of interest, δt=1/6+t for t≥ 2. If both accounts continue to earn interest indefinitely at the levels given above, the amounts in both accounts will be equal at the end of year n. Calculate n. A 23 B 24 C 25 D 26 E 27 v Salma Alsuwailem

Lucas opens a bank account with 1, 000 and lets it accumulate at an annual nominal interest rate of 6% convertible semiannually. Danielle also opens a bank account with 1, 000 at the same time as Lucas, but it grows at an annual nominal interest rate of 3% convertible monthly. For each account, interest is credited only at the end of each interest conversion period. Calculate the number of months required for the amount in Lucas’s account to be at least double the amount in Danielle’s account. A 276 B 282 C 285 D 286 E 288 v Salma Alsuwailem

A business permits customers to pay with a credit card or to receive a percentage discount r for paying cash. For credit card purchases, the business receives 95% of the purchase price onehalf month later. At an effective annual rate of 12%, the two payment methods are equivalent. Determine r. A 4. 55 B 4. 85 C 5. 15 D 5. 45 E 5. 75 v Salma Alsuwailem

During the first four years, interest is credited using a simple interest rate of 5% per year. After four years, interest is credited at a force of interest: δt=0. 2/(1+0. 2 t) , t≥ 4 The following are numerically equal: 1 -the current value at time t=4 of payments of 1, 000 at time t=2 and 400 at time t=7 ; and 2 -the present value at time t=0 of a payment of X at time t=10. Calculate X. A 2, 800 B 2, 840 C 3, 200 D 3, 660 E 4, 200 v Salma Alsuwailem

At time 0, deposits of 10, 000 are made into each of Fund X and Fund Y. Fund X accumulates at an annual effective interest rate of 5%. Fund Y accumulates at a simple interest rate of 8%. At time t, the forces of interest on the two funds are equal. At time t, the accumulated value of Fund Y is greater than the accumulated value of Fund X by Z. Determine Z. A 1, 625 B 1, 687 C 1, 697 D 1, 711 E 1, 721 v Salma Alsuwailem

An investment fund accumulates with force of interest δt=K/(1+(1−t)K) for 0≤t≤ 1 At time zero, there is 100, 000 in the fund. At time one, there is 110, 000 in the fund. The only two transactions during the year are a deposit of 15, 000 at time 0. 25 and a withdrawal of 20, 000 at time 0. 75. Calculate K. A 0. 047 B 0. 051 C 0. 141 D 0. 150 E 0. 154 v Salma Alsuwailem

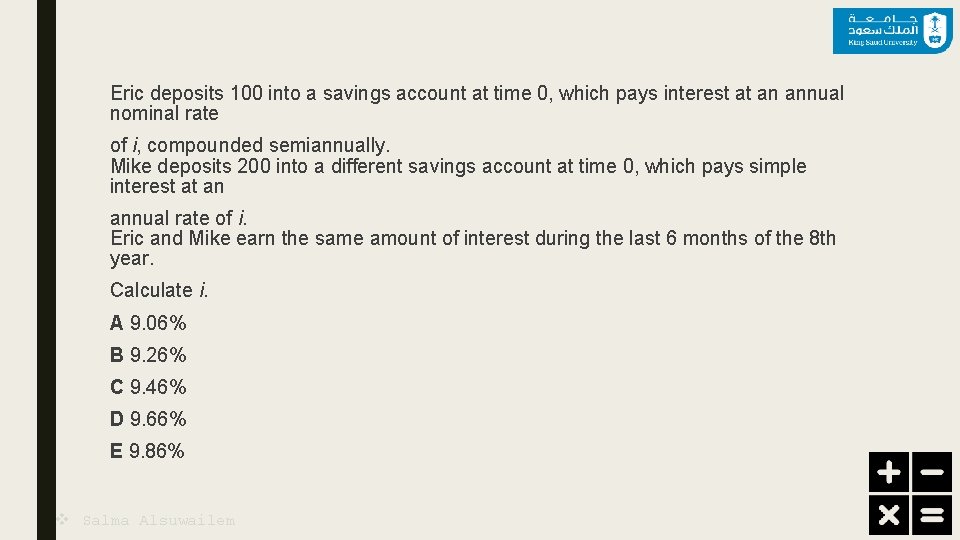
Eric deposits 100 into a savings account at time 0, which pays interest at an annual nominal rate of i, compounded semiannually. Mike deposits 200 into a different savings account at time 0, which pays simple interest at an annual rate of i. Eric and Mike earn the same amount of interest during the last 6 months of the 8 th year. Calculate i. A 9. 06% B 9. 26% C 9. 46% D 9. 66% E 9. 86% v Salma Alsuwailem

You are given: δt=2 t^3+8 t/(t^4+8 t^2+16), 0≤t≤ 1 i is the effective annual interest rate equivalent to δt. Fund X accumulates with simple interest of i. Fund Y accumulates at δt. An amount of 1 is deposited in each of Fund X and Fund Y at time, t=0. At what time, t, is Fund X - Fund Y a maximum? A 0. 250 B 0. 375 C 0. 500 D 0. 625 E 0. 750 v Salma Alsuwailem

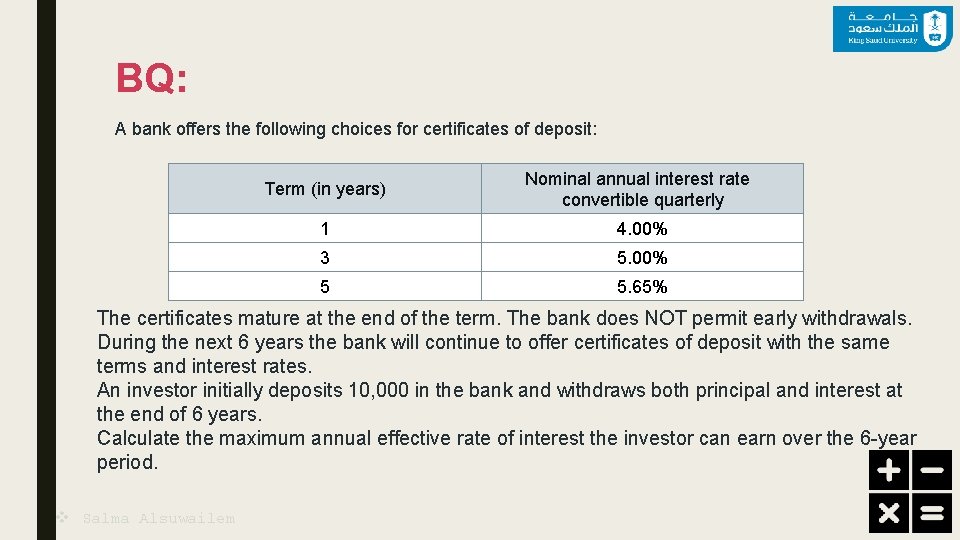
BQ: A bank offers the following choices for certificates of deposit: Term (in years) Nominal annual interest rate convertible quarterly 1 4. 00% 3 5. 00% 5 5. 65% The certificates mature at the end of the term. The bank does NOT permit early withdrawals. During the next 6 years the bank will continue to offer certificates of deposit with the same terms and interest rates. An investor initially deposits 10, 000 in the bank and withdraws both principal and interest at the end of 6 years. Calculate the maximum annual effective rate of interest the investor can earn over the 6 -year period. v Salma Alsuwailem

EXAM FM SAMPLE QUESTIONS FOR CH 1 1 -2 -3 -12 -13 -20 -27 -61 -77 -79 -94 -95 -105 -135 Thank You v Salma Alsuwailem